增量式神经网络聚类算法*

刘培磊，唐晋韬，谢松县，王 挺

(1.国防科技大学 计算机学院， 湖南 长沙 410073；2.国防信息学院 信息化建设系 信息资源管理教研室， 湖北 武汉 430010)



增量式神经网络聚类算法*

刘培磊1,2，唐晋韬1，谢松县1，王 挺1

(1.国防科技大学 计算机学院， 湖南 长沙 410073；2.国防信息学院 信息化建设系 信息资源管理教研室， 湖北 武汉 430010)

神经网络模型具有强大的问题建模能力，但是传统的反向传播算法只能进行批量监督学习，并且训练开销很大。针对传统算法的不足，提出全新的增量式神经网络模型及其聚类算法。该模型基于生物神经学实验证据，引入新的神经元激励函数和突触调节函数，赋予模型以坚实的统计理论基础。在此基础上，提出一种自适应的增量式神经网络聚类算法。算法中引入“胜者得全”式竞争等学习机制，在增量聚类过程中成功避免了“遗忘灾难”问题。在经典数据集上的实验结果表明：该聚类算法与K-means等传统聚类算法效果相当，特别是在增量学习任务的时空开销方面具有较大优势。

神经网络；增量学习；聚类算法；时间开销

随着互联网和社交媒体的广泛发展，大量无标注的数据源源不断地产生[1-2]。这些数据的海量性、无标注性、实时性等特点给传统的机器学习模型带来了很大的挑战[3]。传统的神经网络模型具有强大的问题建模能力，理论上含有足够多隐藏层神经元的神经网络可以逼近任意函数。但是主流的学习算法如反向传播(Back Propergating，BP)算法，使用梯度下降的方法进行学习，是批量监督学习算法，即所有的训练数据必须一次性全部输入学习模型。而模型一旦训练完毕，再碰到新的输入数据时，只能将新数据与旧数据并在一起重新训练模型。这个问题被称为“遗忘灾难”[4]，即新学习的内容会导致已经学习的内容被“遗忘”。 梯度下降的方法带来的另一个问题是训练的时间开销很大，难以在线处理海量的实时性数据[5]。近年来，热门的深度学习模型也面临类似的计算时间开销问题[6]，因此训练规模较大的深度神经网络往往需要使用大规模并行计算集群。自适应共振理论(Adaptive Resonance Theory，ART)模型提出了一套不错的应对办法，它可以快速地进行无监督聚类，并且具有增量学习的特性，在解释人脑工作机制方面也做得比BP网络更充分[4]。然而这种模型也面临着自己的问题，一种典型的质疑是它的理论基础不够坚实，不完全符合统计学原理[7]。ART模型的神经元激励函数、突触连接权重的调节方法等都是经验式的，缺少严格的数学理论支撑。

本文通过借鉴生物神经网络的研究成果，提出了全新的增量神经网络模型IncNet及其无监督聚类算法。主要贡献包括三方面：引入新的神经元激励函数和突触连接权值调节函数，并阐明这些函数背后的统计学意义，使得IncNet模型建立在坚实的统计理论基础之上，为神经网络算法的研发提供一个新的视角和一次有益尝试。在此基础上提出一种全新的神经网络无监督学习算法。鉴于神经网络模型具有强大的问题建模能力，因此神经网络上的无监督学习算法具有重要意义。实际上，深度学习取得成功的一个重要原因就在于将“无监督学习”引入训练阶段。

1 前提与假设

模型的性能与输入数据样本的分布特性是息息相关的，很多模型只有针对特定分布类型的数据才能取得最好的效果。比如贝叶斯网络和支持向量机等都有一个“特征独立性”的假设。基于生物学实验证据，IncNet模型做出第1.1节的合理假设。

1.1 数据分布的假设

时空局部性假设：样本分布在时间和空间维度上具有局部性的特性。

所谓局部性是指相似的样本在时间段内和空间位置上比较接近。以时间局部性为例，样本在时间轴上不是随机分布的，而是簇状聚集的。对应到现实中，事件往往具有突发性[8]。因此，在事件发生的特定时间段上就可以采集到大量的类似样本，而在这个时间之前或者之后采集到的类似样本量就很少。空间局部性的含义与时间局部性类似。

1.2 神经元激励函数

神经元激励函数如式(1)所示。其中，xi是树突输入，wi是突触连接的权值，f(x)是神经元的兴奋值，ci是常数。

(1)

神经学文献表明，一个神经元只有在被激发的时候才会从轴突上释放信号物质，而没被激发的神经元是不释放任何信号物质的[9]。因此IncNet模型认为未激发的神经元不传递信号，而传统模型认为未激发的神经元表示 “0”信号[10]。式(1)的统计意义将会在第2.1.2节进行详细解释。

1.3 突触连接权值调节机制

在真实的生物神经网络中，两个神经元之间由多个突触连接在一起，并且新的刺激会不断地生成新的突触。 传统神经网络模型一般将这些突触简化为单一连接，其中隐含的假设是这些突触的总强度值是单个突触的线性叠加[6]。 而来自神经学的证据表明：连接强度的增长率不是恒定的，而是与当前已有连接强度成负相关的关系[11]。 因此IncNet模型中的突触连接权值非线性增长，如式(2)所示，其中，w表示连接强度，si表示第i次刺激信号生成的突触数。公式(2)的统计学意义将会在第2.3节解释。

(2)

1.4 神经网络的自组织机制

生物神经网络中每个神经元只能知道自身及其直接连接的神经元的信息，即每个神经元知道的信息都是局部的[4]。而BP算法则要求知道整个网络的全局信息，这一点在生物学上难以实现[5]。生物神经网络实际上通过众多神经元的自组织来构建，其中主要的机制之一就是侧向竞争。生物神经元的竞争机制比较复杂，IncNet模型将侧向竞争简化为“胜者得全”的方式。这种编码方式又称为 “祖母细胞(grandmother cell)”编码[12]，即单个输入样本最终映射到单个神经元，受到神经学实验证据的支持。

与“祖母细胞”编码相对应的是传统神经元模型使用的“集体编码(population coding)”方式[12]，即每个输入样本需要多个神经元共同合作来编码。但是，传统神经元模型面临的一个重要问题是“异或”问题[13]，即单层神经网络无法表示非线性函数。而IncNet模型中的单层网络可以解决异或问题，第2.1.4节将会详细叙述。

2 模型与算法

基于第1节的前提与假设，本节提出IncNet模型。在详细介绍问题抽象和模型本身的同时，着重阐述模型的统计学意义。

2.1 模型

2.1.1 问题抽象

IncNet模型面对的问题可以抽象为：对于任意一个输入样本x=(xi)，如何让某个神经元编码这个样本，以便下次遇到类似输入样本的时候，这个神经元会被最大限度地激发。这种编码本质上是神经元通过特定的方案来加强树突连接强度，从而“记住”这个样本。BP神经网络是通过问题空间的梯度下降搜索来逼近这个神经网络编码方案的，这导致时间开销很大[5]，并且找到的编码方案很可能是局部最优点而非全局最优点。

那么能否通过计算的方式直接找到这个全局最佳编码呢？在第1节的前提与假设成立的情况下，理论上是可以通过计算直接找到这全局最优编码方案的。考虑最简单的样本x=(x1,x2),其中xi是[0,1]区间的任意值。现实中每个神经元的树突分支资源(可以形成的突出数量)是有限的，因此问题就变为：一个神经元怎样将其恒定的突触分支资源分配到x1和x2，才能使得自身输入向量x被最大限度地激发呢？这是一个典型的资源优化配置问题，如果突触连接强度是线性增长的，那么神经元倾向于将所有突触分支资源都分配给数值最大的元素xi，达不到“记住”输入模式x的目的。因此资源必须分散到每个输入信号xi，此时式(2)应该是一个单调增长的凸函数。将式(1)、式(2)联立，并加入树突分支资源守恒的约束条件可以得到式(3)。问题抽象为：求出使得f(si)取得最大值的si。很明显最佳的si与xi应该是正相关的。

(3)

这种突触资源分配方案不同于ART等传统模型，ART对单个神经元的树突连接强度做了归一化处理，即单个神经元的所有树突连接强度的总和是一个恒定值[6]。而IncNet模型中式(2)决定了单个神经元所有树突连接强度总和不恒定，恒定的是单个神经元树突分支资源总和。通过这种方式，IncNet模型将神经编码问题转化为了资源优化配置问题。

2.1.2 神经元激励函数的统计意义

假设一个物体有许多特征，并且某一时刻只有其中的n个特征是可见的，那么在此条件下可以正确认定这个物体的概率是多少呢？可以计算出这个概率是：

P(O)=P(O1+O2+…+Ox)=1-P(O1O2…On)= 1-P(O1)P(O2)…

其中，O和Ai分别表示物体及物体的一个特征发生这个随机事件。这个式子可以进一步简化为式(4)，其中xi=lgP(Oi)。

(4)

对照式(1)中的神经元激励函数可以看出：神经元和树突的信号量分别对应概率P(O)和P(Oi)。即神经元信号可以表示物体的发生概率，而树突信号表示物体某个特征发生的概率，因此式(1)具有统计学意义。

2.1.3 突触连接强度的统计意义

式(2)中的突触连接权值变化曲线同样具有统计意义。根据样本分布的时空局部性假设，样本在时间分布上具有时间局部性的特点。假设一个信号出现一次时对应的特征具有某个置信度c，当这个信号多次重复出现的时候，特征信号的置信度c也会增高。具体来说，假设一个信号到目前为止出现了m次，那么与式(4)的推理过程类似，可以得到相应特征的置信度为：

w=c3(1-e-c4m)

(5)

对照式(2)、式(5)可知，突触连接的强度对应物体某一特征的置信度，这个置信度随着刺激信号的重复出现而持续地非线性增长。

2.1.4 侧向竞争与“异或问题”

传统的单层感知机存在“异或问题”，即单层感知机无法表示简单的异或函数，这意味着这个模型的表示能力非常有限[13]。但是在IncNet模型中，单层网络就可以表示异或函数，如图1所示。实际上可以证明，单层网络的IncNet模型可以表示任意布尔函数。

(6)

具体来说，任意逻辑表达式可以转换成式(6)的形式，其中aj是原子公式或者其否定形式。由于输入向量是由互斥的神经元对构成，如图1所示，pi可以使用输出层的单个神经元来表示。只要输出层神经元之间是“或”或者“异或”的关系，P就可以使用单层网络来表示。由于输出层神经元也是互斥的，这个“异或”关系很容易达成。实际上，可以认为图1中的神经元y1，y2和y3分别表示异或函数真值表中的一行，所以图1的网络就可以表示“异或”函数。而异或函数真值表中输出为0的那些行可以用抑制性神经元(即“与非门”)来表示或者省略。

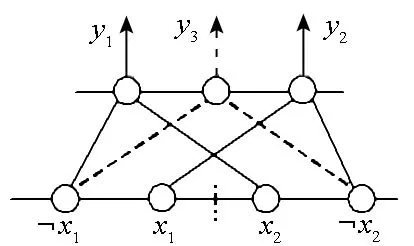
图1 单层网络表示异或函数Fig.1 Single layer network representing “XOR” function

从图1中可以看出，竞争导致IncNet的每一层神经元向量都是稀疏的[14]。单个神经元仅能表示逻辑函数真值表中的一行，而传统模型中单个神经元即可表示整个线性逻辑函数。与传统模型相比，Incnet模型表示能力更强，而代价是需要更多数量的神经元。从信息论的角度看，IncNet模型中的神经元脉冲信号是单值而非二值的，即一个神经元只能表示半比特信息，一比特信息需由两个互斥的神经元来表示。

2.2聚类算法

2.2.1 框架概述

模型如图1所示，形式上与单层感知机比较类似，但是IncNet模型输入向量中的元素存在互斥性而非独立的。并且输出层神经元之间存在“胜者得全”的侧向竞争。关键的不同在于IncNet模型精心选取的神经元激励函数和突触连接权值调节函数使得这个神经网络模型建立在了较为严格的统计学基础上。而BP网络和ART网络等传统模型的神经元激励函数一般是通过经验设定的，通常来说激励函数是一个S型的曲线即可。ART模型的突触连接权值调节函数也是经验式的，并且突触强度会采取归一化的措施。BP网络则完全没有突触连接权值调节函数，是根据误差梯度下降的原则来“试探”得到突触连接权值的。

2.2.2 算法流程

聚类算法的整体思想是：寻找与当前样本最相似的聚类，根据当前样本调整这个聚类的质心使之变得与当前样本更接近。IncNet聚类算法避免了像BP算法一样在问题空间上进行误差梯度下降式搜索，所有的样本只需要逐个进入模型训练一遍即可，因此理论上训练速度会非常快。聚类算法的具体过程如图2所示。每个神经元表示一个聚类，输入样本依次进入IncNet网络模型进行检索，根据匹配的相似度和一个阈值参数共同决定是否新建一个新的神经元或者更新现有的神经元。这个阈值参数实际上控制着聚类的粒度和聚类的数量。

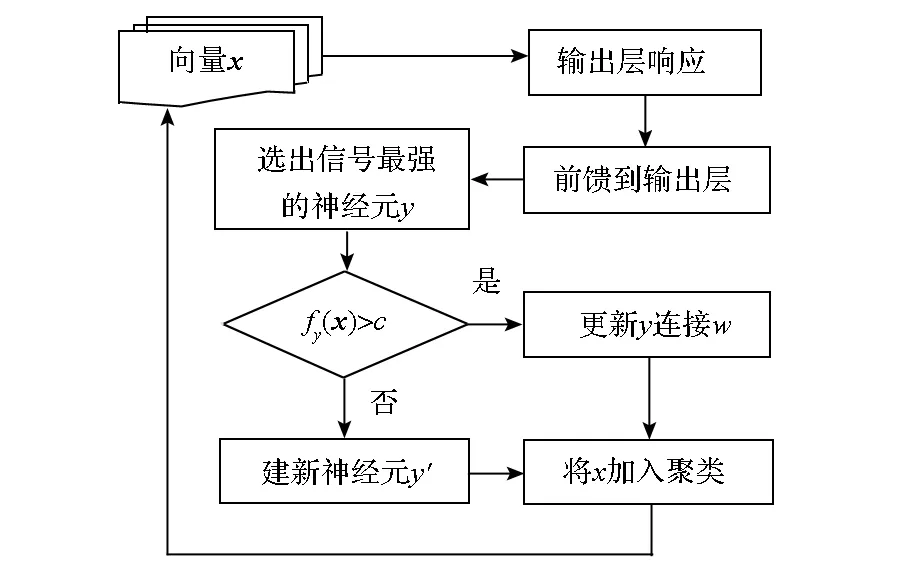
图2 聚类算法流程图Fig.2 Process of clustering algorithm

根据式(2)可知，在聚类过程中突触连接强度是单调增长的，所以新学习的知识不会导致已经学习的旧知识的遗忘，从而避免了BP算法中存在的“遗忘灾难”问题[4]。ART模型对连接强度进行了归一化处理，因此它的突触连接强度不是单调增长的，这导致ART模型只能在一定程度上调和 “遗忘灾难”的问题而无法彻底解决该问题。ART模型对连接强度进行归一化处理是为了避免学习过程中的“偏置”，即最先学习的知识会占据优势。而正如第2.1.3节所述，在时空局部性假设成立的前提下，这种“偏置”在IncNet模型中具有重要的统计意义。

2.3 意义

IncNet模型是一个纯粹的产生式模型，并且每个神经元只与它直接连接的神经元之间交换信息，因此模型具有良好的可扩展性。IncNet模型可以纵向扩展成包含多个层次的深度网络，相邻的层间可以采取类似卷积网络的结构：每个神经元只与前一层的部分神经元连接，而不是全连接。并且IncNet模型从理论上提供了这样一个有益的结论：对符合时空局部性假设的样本数据，存在更快速的办法来进行神经网络的无监督学习。这对深度学习中无监督预训练具有重要意义。传统深度网络中，这种预训练一般是通过梯度下降的方法来进行的，因此时间复杂度很高。此外，IncNet模型在生物神经学方面也有一定的意义。相比BP模型，IncNet模型与现有神经学实验证据吻合度更高。并且作为一个产生式模型， IncNet更容易在生物学和物理学层面进行实现[4]。

3 实验及分析

为了检验新算法的实际效果和时空开销，在两个常用的数据集上与目前主流聚类算法进行比较。这两个数据集原本是为批量学习任务设计的，但是通过将整个数据集分多次输入一个学习模型也可以用来检测增量式学习模型的性能。整个实验分两部分：3.2节将每个数据集视为批量数据，检测新算法在批量学习任务中的性能。3.3节基于3.2节的实验结果，着重分析对比新算法与传统算法在增量式任务上的表现。

3.1 数据集与评价指标

目前IncNet模型只能处理离散型数据，并且没有对程序框架进行时间开销方面的优化。在实现的时候进行了一定程度的简化，比如式(3)的最优解与向量元素之间的约束关系相关，实现的时候将其近似地简化为si=cxi, 即分配的资源数量与输入信号强度成正比例关系。另外，IncNet模型是通过相似度阈值来控制聚类粒度的，而K-means等算法是通过设置聚类数量来控制聚类粒度的。实验中的做法是：先将IncNet的聚类数调节到一个适中数值，然后其他所有算法都将聚类数调整到同一数量进行比较。

Weka是著名机器学习平台[15]，实验选择了Weka平台中的经典聚类算法K-means和期望最大化(Expectation Maximization, EM)作为比较对象，使用的数据集是来自Weka中的vote和breast-cancer两个数据集。实验使用精度作为评价指标。具体地说，将标注好的数据集的标签全部去掉，再使用不同聚类模型对这些数据进行聚类。假设对于第i个聚类，其中相同标签数量最多的样本有ni个，而所有聚类的总数量有n个，那么精度为：

(7)

3.2 批量学习任务实验结果

3.2.1 数据集vote上的批量学习效果

投票数据集vote来自1984年美国国会的投票记录[16]，共包含435个样本数据，每个样本包含16个布尔类型的属性。本实验中主要检测聚类算法的批量学习性能，vote数据集一次性全部输入每个模型进行训练，实验结果见表1。

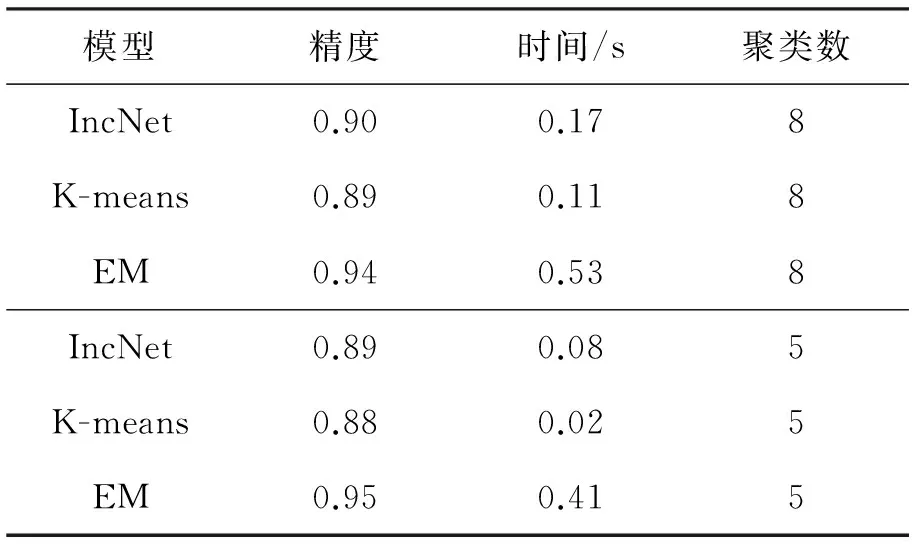
表1 vote数据集上的结果

可以看出，在聚类粒度相同的前提下，IncNet模型的精度和时间开销都介于K-means与EM之间。这个结论在聚类数分别为8和5时都是成立的，稍有不同的是较小的聚类数会导致时间开销的降低。

3.2.2 数据集breast-cancer上的批量学习效果

乳腺癌数据集breast-cancer 于1988年发布，来自南斯拉夫的医学中心大学肿瘤学院[17]，共包含286个样本，每个样本包含9个枚举类型的属性。作为批量学习任务，breast-cancer数据集一次性全部输入每个模型进行训练，实验结果见表2。

表2 breast-cancer数据集上的结果

可以看出这三个模型在breast-cancer数据集上的表现与vote数据集上的表现非常类似，IncNet模型的精度和时间开销仍然介于K-means与EM之间。在两个数据集上的实验结果表明：在批量学习任务上，IncNet模型具有与K-means、EM等常用聚类算法相当的精度和时间开销。

3.3 增量学习任务上的效果

增量学习与批量学习的主要区别是已经训练好的模型对待新输入数据的方式。增量学习模型直接在已有模型基础上进行学习。而批量学习模型则需要抛弃已有模型，将新数据与旧数据并在一起重新学习。将一个数据集比如vote分为多次输入学习模型，实际上这就变为一个增量学习任务了。极端情况下，vote数据集可以分435次输入，即每次只输入一条新的数据。

K-means与EM是批量学习模型，因为它们需要在一次性输入的所有数据上进行反复迭代。为了检验它们在增量学习任务上的性能，可以通过下述方式将其改造为增量学习模型：将已经学习过的样本数据存储起来，每当遇到新输入的数据，就将新数据与存储的旧数据并在一起重新训练模型。在这种条件下，IncNet、K-means与EM的精度仍然如表1和表2所示。此时IncNet的时空开销不变，但是K-means与EM的时空开销发生了较大变化。具体说来，它们产生了额外的存储n个样本的空间开销。而K-means与EM模型在表1与表2中的时间开销就变为它们学习最后单独一条样本数据时的时间开销，因此总的时间开销要比表中数值大得多。可见，在增量学习任务上，IncNet的精度与常用聚类算法相当，但是在时间和空间开销上具有很大的优势。

4 结论

本文通过借鉴生物神经学实验证据，提出了全新的增量式神经网络模型及其聚类算法。通过引入新的神经元激励函数与突触连接权值调节函数，赋予神经网络学习算法以严格的统计意义。尝试将神经网络强大的问题表示能力与统计学习理论进行结合，为新型神经网络学习算法的研发提供了新的视角。在此基础上提出了一种快速增量无监督聚类算法。在经典数据集上的实验结果表明，在批量学习任务中，IncNet与K-means等算法的精度和时空开销相当。但是在增量式学习任务中，IncNet模型在时空开销方面具有较大优势。

References)

[1] Xie S X, Wang T. Construction of unsupervised sentiment classifier on idioms resources[J]. Journal of Central South University, 2014, 21(4): 1376-1384.

[2] Wang X, Jia Y, Chen R, et al. Improving text categorization with semantic knowledge in Wikipedia[J]. IEICE Transection on Information System， 2013, 96(12): 2786-2794.

[3] 张志, 廖瑛, 余越. BP神经网络在极移预报中的应用[J]. 国防科技大学学报, 2015, 37(2): 156-160.

ZHANG Zhi, LIAO Ying, YU Yue. Application of BP neural network model in prediction of polar motion[J]. Journal of National University of Defense Technology, 2015, 37(2):156-160.(in Chinese)

[4] Grossberg S. Adaptive resonance theory: how a brain learns to consciously attend, learn, and recognize a changing world[J]. Neural Networks, 2012, 37: 1-47.

[5] Rumelhart D E, McClelland J L. Parallel distributed processing: exploration in the microstructure of cognition[M]. USA: MIT Press, 1988.

[6] Hinton G E, Osindero S, Teh Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18: 1527-1554.

[7] Warren S S. Why statisticians should not FART [EB/OL]. (1995)[2015-09-10]. ftp://ftp.sas.com/pub/neural/fart.txt.

[8] Liu P L, Tang J T, Wang T. Information current in Twitter: which brings hot events to the world[C]// Proceedings of 22nd International World Wide Web, 2013： 111-112.

[9] Hodgkin A L, Huxley A F. A quantitative description of membrane current and its application to conduction and excitation in nerve[J]. Bulletin of Mathematical Biology, 1990, 52(1/2): 25-71.

[10] 刘开宇, 侯振挺. 一类具M-P型非线性二元神经网络模型的周期解[J]. 国防科技大学学报, 2008, 30(4): 129-132.LIU Kaiyu, HOU Zhenting. The periodic solution of a neural networks of two neurons with McCulloch-Pitts nonlinearity[J]. Journal of National University of Defense Technology, 2008, 30(4): 129-132. (in Chinese)

[11] Bienenstock E L, Cooper L N, Munro P W. Theory for the development of neuron selectivity: orientation specificity and binocular interaction in visual cortex[J].Journal of Neuroscience the Official, 1982, 2(1): 32-48.

[12] Gross C G. Genealogy of the “grandmother cell”[J]. Neuroscientist, 2002, 8(5): 512-518.

[13] Minsky S P. Perceptrons: an introduction to computational geometry[M]. UAS: MIT Press, 1972.

[14] Olshausen B A. Sparse codes and spikes[J]. MIT Press, 2002: 257-272.

[15] Hall M, Frank E, Holmes G, et al. The WEKA data mining software: an update[J].ACM Sigkdd Explorations Newsletter, 2009, 11(1): 10-18.

[16] Schlimmer J C. Concept acquisition through representational adjustment[D]. USA: University of California, 1987.

[17] Tan M, Eshelman L. Using weighted networks to represent classification knowledge in noisy domains[C]//Proceedings of the Fifth International Conference on Machine Learning, 1988: 121-134.

Incremental clustering algorithm of neural network

LIU Peilei1,2, TANG Jintao1, XIE Songxian1, WANG Ting1

(1. College of Computer, National University of Defense Technology, Changsha 410073, China;2. Teaching and Research Section of Information Resource Management, Department of Information Construction,Academy of National Defense Information, Wuhan 430010, China)

Neural network model is powerful in problem modelling. But the traditional back propagating algorithm can only execute batch supervised learning, and its time expense is very high. According to these problems, a novel incremental neural network model and the corresponding clustering algorithm were put forward. This model was supported by biological evidences, and it was built on the foundation of novel neuron’s activation function and the synapse adjusting function. Based on this, an adaptive incremental clustering algorithm was put forward, in which mechanisms such as “winner-take-all” were introduced. As a result, “catastrophic forgetting” problem was successfully solved in the incremental clustering process. Experiment results on classic datasets show that this algorithm’s performance is comparable with traditional clustering models such as K-means. Especially, its time and space expenses on incremental tasks are much lower than traditional clustering models.

neural network; incremental learning; clustering algorithm; time expense

10.11887/j.cn.201605021

http://journal.nudt.edu.cn

2015-09-28

国家自然科学基金资助项目(61532001，61472436)

刘培磊(1984—)，男，江苏连云港人，博士研究生，E-mail：plliu@nudt.edu.cn；王挺(通信作者)，男，教授，博士，博士生导师，E-mail：tingwang@nudt.edu.cn

TP393

A

1001-2486(2016)05-137-06