单逆变器驱动双PMSM的最大转矩电流比控制

梁康有，袁 玲，程正富

(1.重庆文理学院，重庆 402160；2. 国网重庆市电力公司 永川供电分公司，重庆 402160)



单逆变器驱动双PMSM的最大转矩电流比控制

梁康有1，袁 玲2，程正富1

(1.重庆文理学院，重庆 402160；2. 国网重庆市电力公司 永川供电分公司，重庆 402160)

针对单逆变器驱动双永磁同步电动机(PMSM)驱动系统负载不平衡失稳问题，引入加权系数km建立双PMSM的等效加权数学模型，并基于该等效模型设计双PMSM最大转矩电流比(MTPA)控制方法。该方法实现了双PMSM矢量控制系统等效模型的实时修正，包含定向角度、激磁电流和转矩电流。此外，无最大电流约束和电流限幅边界约束两种情况下的双PMSM最优MTPA曲线被分别讨论，同时将系统运行效率与传统id=0方法在全转速、负载范围进行对比分析。最后，基于双15 kW PMSM调速系统实验平台进行验证与分析，包括双PMSM动、稳态及运行效率等多项指标。结果表明，所提双PMSM的MTPA控制方法具有一定的理论意义和现实价值。

双机驱动；等效模型；永磁同步电动机；最大转矩电流

0 引 言

近年来由于多电机在造纸、纺织、炼钢、城市轨道交通等领域中的广泛应用，使得多电机的驱动技术成为研究热点[1-3]。对多电机系统的研究通常被简化为对多个电机独立系统的研究，文献[4]基于最小相关轴数目的同步控制思想，解决了大型高精度、高转速传动系统的多电机同步控制问题；文献[5-6]研究了两电机驱动的三相、四相、五相电压源逆变器的拓扑结构，并将其应用到多相电机的控制系统中；文献[7-8]将电压源逆变器的桥臂数推广到(2n+1)，并提出n台电机驱动系统的拓扑结构。然而，传统三相单逆变器驱动多电机凭借其结构、成本等诸多优势，仍为工业现场多电机驱动的主要方案[9-10]。

针对单逆变器驱动双永磁同步电动机(以下简称PMSM)驱动系统负载不平衡失稳问题，本文引入加权系数km建立双PMSM的等效加权数学模型，并基于该等效模型设计双PMSM最大转矩电流比(以下简称MTPA)控制方法。该方法实现了双PMSM矢量控制系统等效模型的实时修正，包含定向角度、激磁电流和转矩电流。此外，无最大电流约束和电流限幅边界约束两种情况下的双PMSM最优MTPA曲线被分别讨论，同时将系统运行效率与传统id=0方法在全转速、负载范围进行对比分析。最后，基于双15 kW PMSM调速系统实验平台进行验证与分析，包括：双PMSM动、稳态及运行效率等多项指标。结果表明，所提双PMSM的MTPA控制方法具有一定的理论意义和现实价值。

1 单逆变器双PMSM矢量控制原理

图1为单逆变器驱动双PMSM系统概述图。对于独立的三相理想对称PMSM驱动系统，可建立其两相旋转dq坐标系下的电压、转矩方程：

图1 单逆变器双PMSM矢量控制原理

(1)

(2)

(3)

(4)

式中：Te为电机电磁转矩；p为电机极对数；ψm为永磁体磁链；id，iq为d，q轴定子电流；Ld，Lq为d，q轴电感；Bm为传动系统摩擦系数；J为电机负载转动惯量。

考虑到两台PMSM实时转子位置的不一致性，引入加权系数km进行双PMSM矢量控制系统定向角度、激磁电流、转矩电流修正。其中，在旋转dq坐标系下PMSM交变分量均可变换为直流分量，为此建立双PMSM等效转子磁链坐标系下磁链、电流、角速度的加权值和误差值如下：

(5)

(6)

(7)

式中：ψr为双PMSM加权转子磁链矢量，并将如图2所示的定向坐标系定义为“加权转子磁链旋转坐标系”，其中d轴与加权转子磁链矢量ψr同方向。dq坐标系下转子磁链、电机电流矢量描述：

图2 电流矢量角β对应转矩Te变化规律

(8)

进一步建立双PMSM转矩表达式：

(9)

将式(5)、式(6)代入式(9)得双PMSM转矩之和：

(10)

式中：ψr1-(1±kmΔψr)为km修正后的双PMSM等效转子磁链；is-(1±kmΔis)为km修正后的等效电流。

至此，分析式(10)可知加权系数km物理意义为在双PMSM负载不平衡情况下优化系统动态响应特性，故将其定义：

(11)

假设双PMSM驱动系统出现负载转矩不平衡现象，其中1#电机负载转矩突增即对应加权系数km增加，此时双机矢量控制系统以1#电机为主电机控制，保证1#电机转速快速恢复其期望值。

2 双PMSM驱动系统MTPA模型

假设两台PMSM参数保持一致，实际系统运行过程中双机转子位置随负载特性不同存在差异性。考虑到双PMSM由同一逆变单元驱动，其定子端电压保持相同，即电压矢量幅值满足以下关系：

(12)

将式(3)进行简化分析可得：

(13)

此外，考虑到双PMSM系统安全性需满足以下电流限制约束，即得双PMSM驱动系统约束方程：

(14)

(15)

分析式(8)可知，对于期望的转矩电流iq1、iq2工作点存在多组(id1,id2)满足要求，此时引入双PMSM铜损方程，即：

(16)

考虑到PMSM输出电磁转矩由实际负载转矩直接决定，即iq1、iq2由负载转矩直接决定。因此，将双PMSM驱动系统损耗模型简化：

(17)

至此，由式(8)、式(12)构建拉格朗日极值方程：

(18)

式中：λ为拉格朗日约束因子。对式(18)各变量进行偏微分处理得：

(19)

当且仅当式(19)中拉格朗日微分方程均为零时，双PMSM驱动系统铜损最小，即：

(20)

图3 双PMSM驱动系统MTPA轨迹图解结果

3 双机MTPA电流限幅边界约束问题

在实际双PMSM驱动系统运行时，逆变器需满足式(14)～式(15)的最大输出电流限制。然而，当负载转矩足够大时，存在电机电流等于额定值的特殊情况，即为双机MTPA电流限幅下的边界约束问题。此时，假设1#电机电流达到其最大限幅值，修正后的双机d轴电流：

(21)

式中：双机驱动系统运行于1#电机电流限幅边界，同时表明动态操作过程中iq1大于iq2。

图4给出了计及双机电流限幅的MTPA边界约束解修正结果。其中，当负载转矩为Te2,high时，系统可运行于MTPA最优轨迹，此时O点位于电机最大电流圆以内；当负载转矩为Te2,low时，系统无法保证MTPA最优轨迹运行，工作点由MTPA最优工作点P修正至Q，Q点位于电机最大电流圆的边界处。

图4 计及双机电流限幅的MTPA修正结果

图5为额定转速1pu时，不同负载工况下d轴电流幅值对比结果，图5中无论轻载或重载MTPA对应d轴电流幅值均小于id=0方法。可以看出，当采取MTPA方法进行双机系统损耗优化时，其最大电流幅值可缩小30%以上。图6给出了双机驱动系统MTPA优化方法控制流程。其中，是否达到电流幅值边界约束，将作为核心判据决定真实作用于双PMSM的d轴电流。

图5 额定转速1 pu时，不同负载工况下d轴电流幅值对比结果

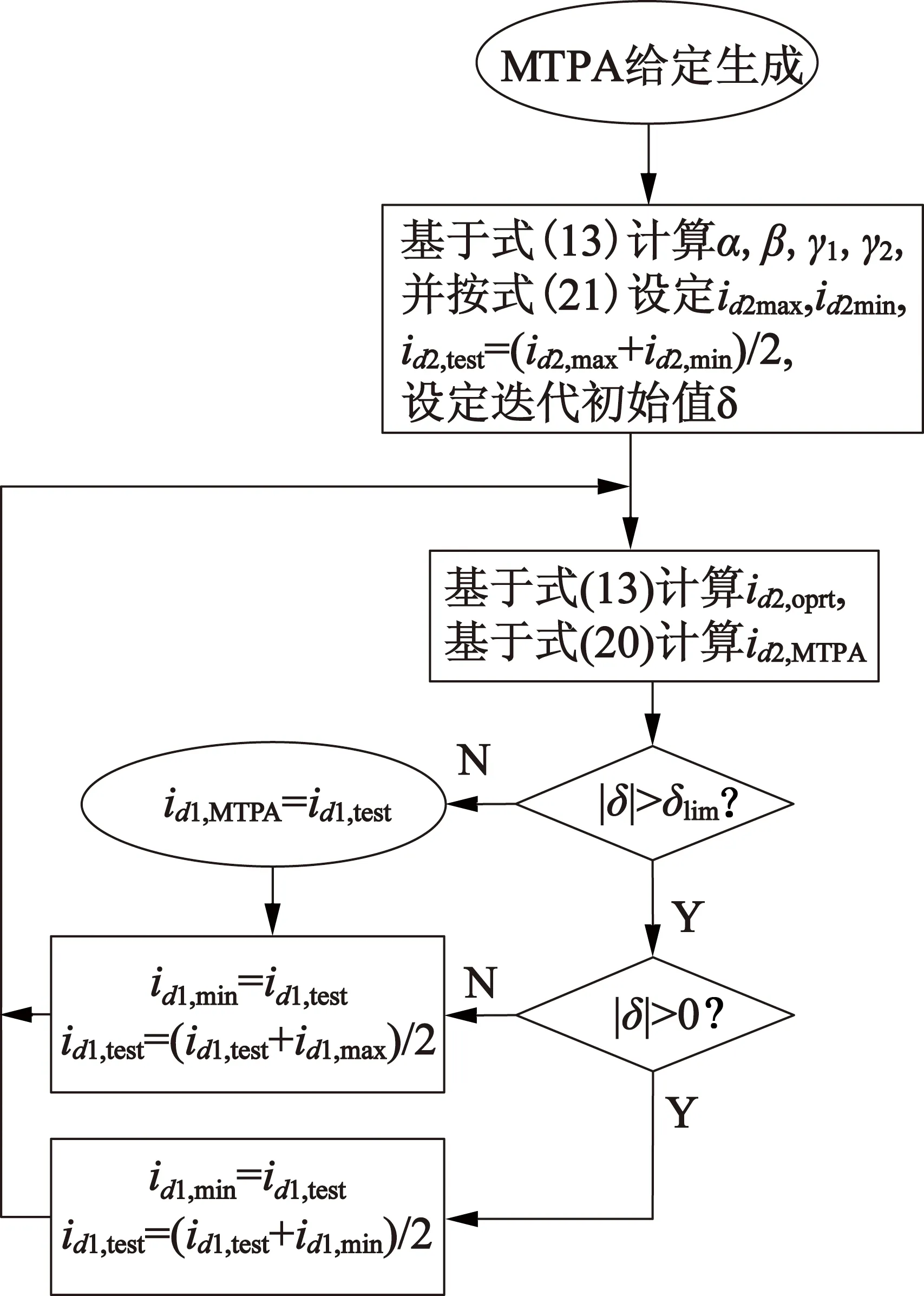
图6 双机驱动系统MTPA优化方法控制流程

4 实验验证

4.1 实验平台及方案

为了验证所提单逆变器驱动双PMSM的MTPA控制方法的可行性和有效性，基于如图7所示的双15 kW PMSM调速系统实验平台进行验证与分析。核心处理器为TI公司浮点型的TMS320F28335型DSP，其主要完成双机矢量控制、MTPA以及SVPWM调制算法运行，同时完成系统对外通信扩展。协处理器为Xilinx公司Spartan 6E型号FPGA，其主要完成AD采样、数据存储等功能，CPLD主要完成PWM状态检测、死区补偿、脉冲封锁等功能。

图7 双15 kW PMSM调速系统实验平台

图8为单逆变器驱动双PMSM的MTPA控制系统软件框图，其中：权值系数计算单元和转速外环控制单元将双PMSM驱动系统等效为一个统一的电机，系统根据双PMSM负载转矩的变化进行电机模型自适应修正，以保证系统的稳定性和动态跟随性能。MTPA磁链优化单元以图7所示控制流程进行双PMSM动态磁链优化，电流限幅边界约束环节的加入保证了理论优化解的可行性。

图8 单逆变器驱动双PMSM的MTPA控制系统软件框图

4.2 实验结果及分析

图9给出了双PMSM驱动系统稳态电流波形，其中：1#电机为重载50 N·m负荷，2#电机为轻载20 N·m负荷。可以看出，1#、2#电机电流幅值分别是30 A和15 A，频率均为50 Hz，表明双PMSM在单逆变器驱动下均工作于额定转速，但其输出转矩存在差异。此时，基于加权系数km建立的双PMSM等效加权数学模型中1#电机占主导地位，1#电机为主电机、2#电机为从电机。上述主从关系并非固定不变的，随着1#、2#电机负荷强度的变化，其主、从关系及加权系数km也随之变化，验证了双PMSM矢量控制系统等效模型的实时修正方法的优越性。

图10为双PMSM驱动系统动态电流波形，其中：1#电机保持空载特性不变，2#电机在200 ms时负载由空载突增至100%。可以看出，2#电机由于负载突增出现转速扰动，最大扰动范围达到100 r/min，扰动持续时间达到300 ms；反观1#电机，其运行转速并未随2#电机负载波动而变化，两台电机呈现出优异的解耦特性。进一步分析对应上述调节过程的dq轴电流可知，1#电机d轴电流随2#电机负载突增而变化，该过程实质为双PMSM电机模型修正过程，矢量控制定向角θr在该过程中被重新定标，保证双PMSM驱动系统的动态抗扰动性能。

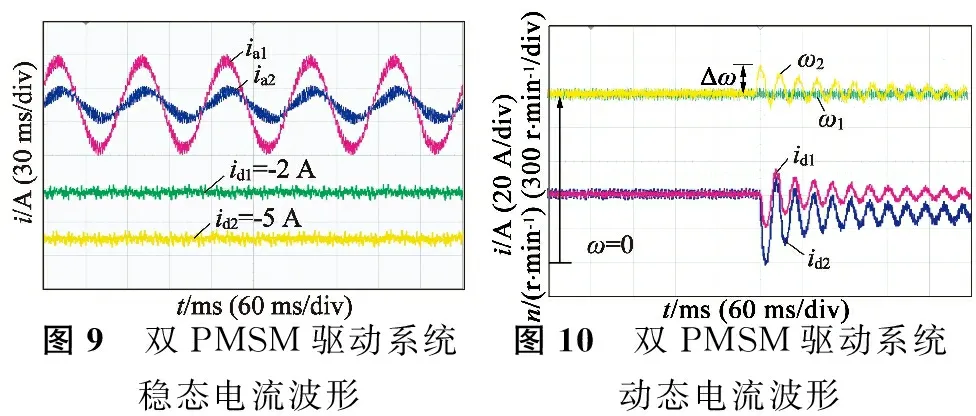
图9 双PMSM驱动系统稳态电流波形图10 双PMSM驱动系统动态电流波形

图11为双PMSM驱动系统MTPA和id=0方法损耗对比结果，其中：电机转速运转在500 r/min至1 500 r/min，负载转矩保持恒定为71 N·m，转速变化步长为500 r/min。图11数据表明，MTPA、id=0两种方法均可实现双PMSM驱动系统高效率运行，其系统全局效率值均可达到80%以上。差异性表现在，MTPA不仅考虑了PMSM的效率最优化，电机驱动系统损耗的引入使得系统全局效率值更高，且上述差异性随着电机转速的增加逐步放大。

图11 双PMSM驱动系统MTPA和id=0方法损耗对比结果

5 结 语

本文针对单逆变器驱动双PMSM驱动系统负载不平衡失稳问题，本文引入加权系数km建立双PMSM的等效加权数学模型，并基于该等效模型设计双PMSM MTPA控制方法。双15 kW PMSM调速系统实验平台验证所提方法的可行性，并得出以下结论：1) 双PMSM矢量控制系统等效模型可根据电机负载波动实时修正系统模型，保证了双机驱动系统优异的动、稳态性能；

2) 计及电流限幅边界约束问题的双机MTPA优化方法，可实现全负载特性范围内的系统效率最优。

[1] MENGONI M, TANI A, ZARRI L, et al.Position control of a multi-motor drive based on eries-connected five-phase tubular PM actuators[J].IEEE Transactions on Industry Applications,2012,48(6):2048-2058.

[2] 李建勇,王勤,戴先中,等.多电机同步系统的解耦控制[J].控制工程,2015,10(2):169-172.

[3] 张小刚.矿用电机分布式控制与保护装置的设计[J].煤矿机械，2013,34(5)：179-181.

[4] 王德春.多电机横向布置电牵引采煤机的设计[J].煤矿机械,2015,32(5):10-12.

[5] 张承慧,石庆升,程金.一种基于相邻耦合误差的多电机同步控制策略[J].中国电机工程学报,2007,27(15):59-63.

[6] 刘东,黄进,于文娟,等.空间矢量PWM多相变频调速系统非正弦供电技术[J].电机与控制学报,2010,14(9):41-47.

[7] CHO J,BAEK J,RIM G,et al.Novel zero voltage transition PWM multi-phase converters[C]//Eleventh Annual Conference,Proceedings of Applied Power Electronics Conference and Exposition,1996.IEEE,1996:500-506.

[8] DUJIC D,JONES M,VUKOSAVIC S N,et al.A general PWM method for a (2n+1) leg inverter supplying n three-phase machines[J].IEEE Transactions on Industrial Electronics,2009,56(10):4107-4118.

[9] 焦宁飞,刘卫国,张华,等.一种变励磁无刷同步电机最大转矩电流比控制方法[J].微特电机,2013,41(1):4-6.

[10] FOO G,RAHMANahman M F.Sensorless sliding-mode MTPA control of an IPM synchronous motor drive using a sliding-mode observer and HF signal injection[J].IEEE Transactions on Industrial Electronics,2010,57(4):1270-1278.

MTPA Control Method of a Single Inverter Double PMSM System

LIANGKang-you1,YUANLing2,CHENGZheng-fu1

(1.Chongqing University of Arts and Sciences, Chongqing 402160,China; 2.Chongqing Electric Power Company， State Grid,Chongqing 402160,China)

The problem of load imbalance instability in drive system occurs when permanent magnet synchronous motors was driven by single inverter system. Weighting coefficientkmwas introduced to establish equivalent weighted mathematical model of double PMSM and the maximum current per ampere control method was designed based on the equivalent model of double PMSM. The real time correction of the double PMSM equivalent model in vector control system was implemented by this method, including orientation angles, exciting current and the current of torque. In addition, the optimal MTPA curves in the cases of double PMSM without maximum current constraints and current limiting boundary were discussed separately. Meanwhile, compared with the method of traditionalid=0, the operating efficiency of the system was analyzed comparatively at full speed and load range. Finally, double 15 kW PMSM speed control system based on experimental platform for validation and analysis, including a number of indicators such as double PMSM dynamic，static and operational efficiency. Results show that the MTPA of PMSM control method is of theoretical significance and practical value.

double motors driven; equivalent model; permanent magnet synchronous motor (PMSM); maximum current per ampere(MTPA)

2015-11-16

国家自然科学基金项目(51377020)

TM341;TM351

A

1004-7018(2016)08-0105-04

梁康有(1974-)，男，硕士，讲师，主要研究领域为电力系统电气控制、电路与系统。