基于磁固耦合的分数槽永磁同步电动机振动分析

左 佳，郭瑶仙，全 鑫

(天津大学，天津 300072)



基于磁固耦合的分数槽永磁同步电动机振动分析

左 佳，郭瑶仙，全 鑫

(天津大学，天津 300072)

以小型分数槽永磁电机为研究对象，通过分析其电磁振动理论，从多方面对电机结构进行了优化。把计算出的电磁力离散成点并加载到电机定子上，在ANSYS中做了瞬态动力学分析，最终得到电机定子对动载荷的时域响应。但瞬态动力学分析只能近似获得电机某点的时域响应，并不能得到整个电机精确的动力学特性曲线。而采用磁固耦合联合仿真可将计算出的电磁力自动耦合到定子齿做频谱分析，从而得到电机整体的频谱特性。结果表明采用磁固耦合的方法更能精确的反映电机振动的频谱特性，从而指导电机结构设计以及优化。

分数槽永磁同步电动机；频谱分析；磁固耦合；电机振动

0 引 言

永磁同步电动机的振动主要有电磁振动，机械振动，和空气动力振动，其中电磁振动是最复杂，最难消除的。电磁振动是由于气隙中的各次磁密波相互作用产生的[1]。电磁力作用于电机定子上，使定子产生形变。而在永磁电机中，电机气隙磁密取决于永磁磁动势，定子绕组磁动势和气隙磁导，所以分析电磁振动主要集中在分析定子绕组磁动势，转子永磁磁动势，以及气隙磁导。而电磁力波引起的振动位移还与力波阶数的4次方成反比，力波阶数与电机槽极配合相关[2-7]。国内唐任远、陈益广、王秀和、杨浩东、国外褚自强等人对电机振动的抑制方法多集中在增加辅助槽，减少齿槽转矩，注入谐波电流，以及减少电磁力等方法[8-14]，而没有考虑电机振动的频谱特性，而且分析的电机体积功率较大，对于小微电机有些理论不一定适合。本文针对小微型电机(9/8，12/10)对其从槽极配合，齿槽转矩，开辅助槽，以及永磁的合理选用四方面对电机进行分析，而后将每个定子齿表面离散为5个点，利用有限元软件计算出每个点的受力(随时间变化的函数)，施加到各个定子齿上，得到其时域的振动位移，但这种传统的方法所得的位移图像不精确，而且离散点个数的选取对结果影响较大。本文又采用磁固耦合方法，软件自动将电磁力自动耦合到电机定子齿上做振动分析，得到电机各点振动位移的频谱响应，更接近实际情况，能更好的指导电机的结构设计。

1 电磁振动的理论分析

1.1 电磁力波的构成

气隙磁密由永磁磁动势、电枢磁动势与气隙磁导相互作用产生，其通用表达式：

式中:Bν为定子谐波磁场(当v=p为基波)；Bμ为转子谐波磁场；Bνλ1为定子齿谐波磁场；Bμλ1为永磁齿磁导谐波磁场。

电机径向力表达式:

(2)

式中：B(θ,t)为气隙磁密;pn(θ,t)电磁径向力密度;μ0为真空磁导率。

将式(1)代入式(2)就可得到各阶力波的频率和幅值。将4种磁密用a,b,c,d简易表示，则得:

(3)

再用和差化积公式，就可得到每种力波的幅值、频率、阶数。

定子振动位移的关系式:

(4)

式中:δ为振动位移;E为弹性模量;ρ为密度;L为电机长度;m为力波模数;p为电磁力波密度;Ro为定子外径;Ri为定子内径。

将式(4)化简：

(5)

由振动位移公式可知只有阶数低，振动幅值大的力波才会引起大的振动。所以去除那些阶数高幅值小的力波，简化后的力波可以表示:

(6)

由式(6)可知电磁力波主要由定子电枢绕组基波、定转子的谐波和定子谐波磁场与永磁齿磁导谐波磁场相互作用三部分组成。

1.2 不同齿槽配合的电磁力波分析

当槽数为奇数时，电枢绕组会产生除极对数3以及3的倍数以外所有的磁动势，即1，2，4，5，7，8，10，11……对极磁动势；当槽数为偶数时，电枢绕组会产生除极对数为偶数和3以及3的倍数的磁动势，即产生1，5，7，11，13，17，19……对极磁动势。8极9槽是典型的奇数槽，10极12槽是典型的偶数槽，用有限元软件仿真得到的电枢磁动势如图2所示。

图1 两种极槽配合的二维模型

(a) 8极9槽

(b) 10极12槽

其中8极9槽4对极为基波，5对极为幅值最大的谐波；10极12槽5对极为基波，7对极为幅值最大的谐波。这也是分数槽电机电磁振动较大的主要原因。由上述的分析，电磁力波主要由定子绕组磁动势与永磁体磁动势相互作用产生，以及定子绕组磁动势与永磁齿磁导谐波磁动势相互作用。所以列出产生电磁力波的主要成分，8极9槽和10极12槽的力波情况如表1和表2所示。其中8极9槽，4对极为基波，规定基波旋转方向为正，其它对极转向相同时为正，相反时为负。同样，10极12槽，5对极为基波，其他对极转向相同时为正，相反时为负。μ为转子磁场极对数，v为定子磁场极对数，μ±k1Z1为

表1 8极9槽电机主要力波表

表2 10极12槽电机主要力波表

转子齿谐波极对数，Z1为槽数，在表1中Z1取9，表2中Z1取12。忽略二阶齿谐波，k1取1，因为高阶的磁动势幅值越来越小，仅列出主要的力波频率。

利用有限元软件可求出径向力波，在气隙圆周处对其进行傅里叶分解，可得到图3。

(a) 8极9槽

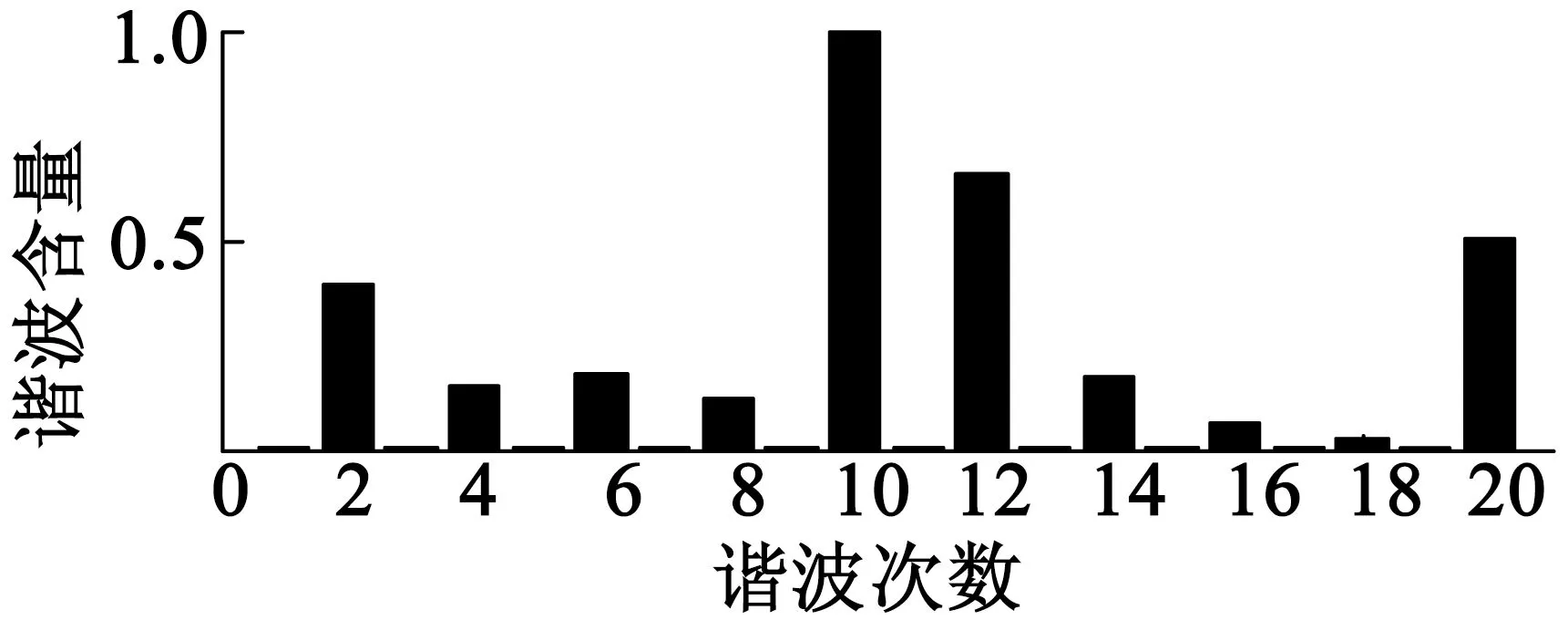
(b) 10极12槽

由图3可知，8极9槽的低阶力波含有所有阶力波，而且1阶力波幅值很大，即单边磁拉力很大，使电机产生很大的振动。10极12槽的低阶力波含有2，4，6次，引起的振动位移相比8极9槽要小的多。由上述分析可知，8极9槽的电机振动较大，所以下面主要分析8极9槽电机的性能来探讨如何减弱小微型电机的振动。

2 8极9槽电机有限元仿真分析

永磁同步电动机主要参数如表3所示。图4为电机空载时磁力线分布图。用Ansoft软件在电机气隙处画圆，求取的气隙磁密如图5所示。

表3 永磁同步电动机主要参数

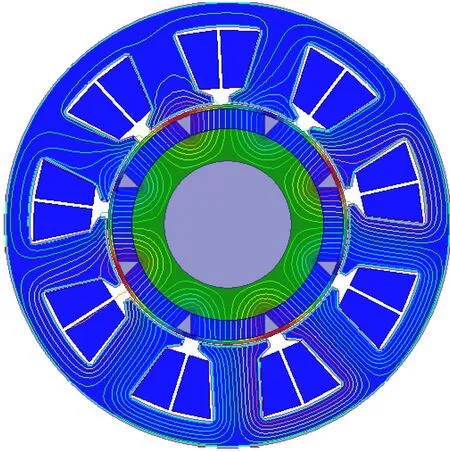
图4 空载磁力线分布图

图5 气隙处圆周磁密图

电机径向磁拉力是气隙磁场与电机定子关于时间和位置的函数,如图6、图7和图8所示。

图6 圆周径向磁拉力密度图

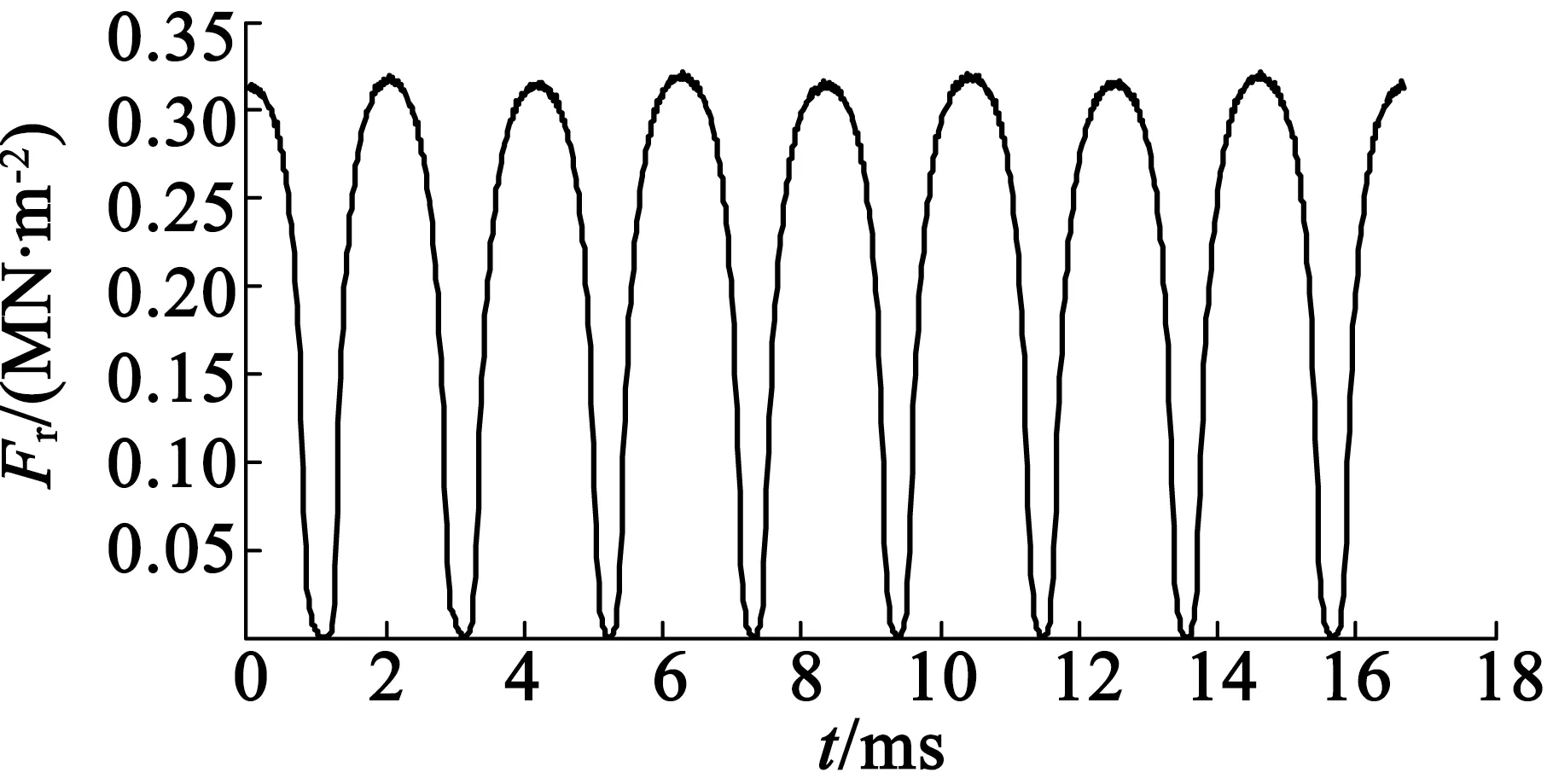
图7 气隙某点随时间变化磁拉力密度图

图8 径向磁拉力随时间空间的三维图

3 电机结构的分析及优化

电机气隙磁密取决于永磁磁动势、定子绕组磁动势和气隙磁导，所以分析振动的根源也是从这三方面入手。

永磁磁动势大小和充磁方向有关，传统的充磁方向为径向充磁和平行充磁，平行充磁较为简单，但是平行充磁的充磁厚度不均匀，永磁磁动势的谐波含量也与径向充磁不同；定子绕组磁动势可通过增加辅助槽的方式间接改变槽极配合的方式来改变，开辅助槽的方式尝试过在空间对称开3个槽，如图9(a)所示，构成12槽8极，但是这样导致空间磁路不对称。如果在每个齿上开一个槽构成18槽8极，如图9(b)所示。此时齿部磁密幅值已经较高，若开辅助槽则导致齿部高度饱和，造成铁损增大，导致电机发热，导致绝缘老化，严重时造成线圈匝间短路，烧毁电机。所以对于小电机开辅助槽虽然能够减少齿槽转矩径向力波幅值，但是缺点也很多。

(a) 3个辅助槽

(b) 9个辅助槽

对于气隙磁导，增大气隙长度固然可以有效地减少振动，但是增大气隙长度会导致磁阻变大、电机出力和反电动势性能都减小。由于气隙磁导和槽开口大小关系紧密，所以可以通过改变槽开口大小来改变气隙磁导。而极弧系数的改变更多的是为了减少齿槽转矩。对于隐极式永磁同步电动机，齿槽转矩容易引起振动噪声等一系列问题。图10与图11是对极弧系数优化之后的对比图。

图10 改变极弧系数前的齿槽转矩图

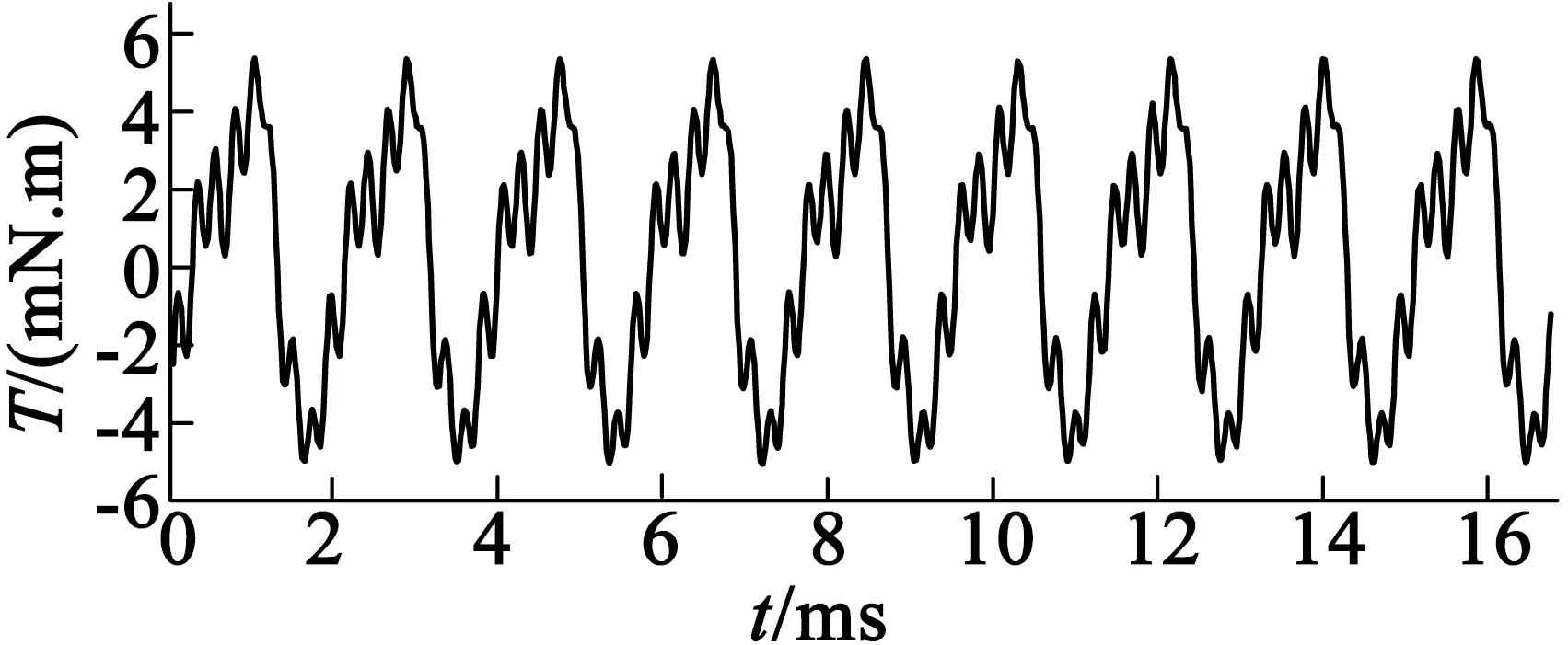
图11 改变极弧系数后的齿槽转矩图

磁极常见的有同心圆式和等半径式，磁铁的充磁方向也有径向充磁和平行充磁，所以可以组合出4种磁极的方式，利用有限元软件放出4种不同磁极的空载反电动势，观测其谐波含量，谐波含量越少，振动力波也越小。在加工过程中，同心圆式永磁体比等半径式材料利用率低，而径向充磁也比平行充磁工序复杂。

利用软件，在其他变量都相同的情况下分析4种组合单相反电动势，如图12所示。

图12 单相反电动势图

图13 单相反电动势傅里叶分解图

由图13可知，平行充磁的同心式和等半径式性能基本相同，反电动势高，傅里叶分解有3次谐波，星形连接之后3次谐波就消失了，其他谐波分量也较少，设计满足要求综合加工成本和性能，所以选择等半径式平行充磁的永磁体。

4 模态分析与磁固耦合分析

电机定子材料参数如表4所示，定子模态图如图14所示。

表4 电机定子材料属性

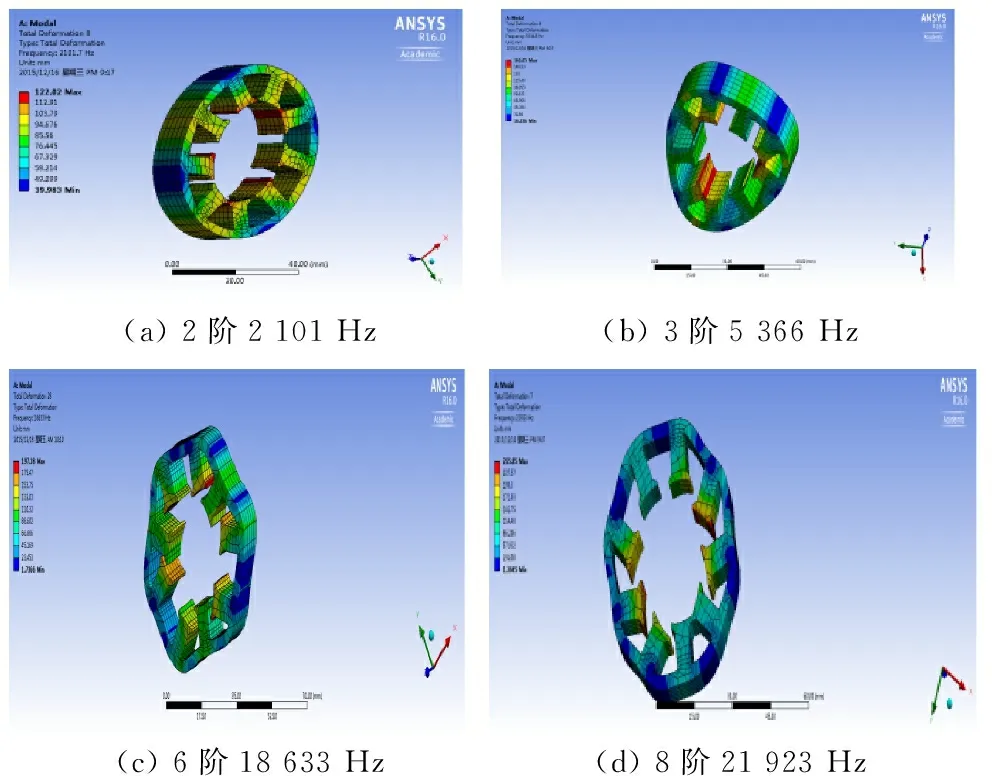
(a)2阶2101Hz(b)3阶5366Hz(c)6阶18633Hz(d)8阶21923Hz

图14 电机定子模态图

由于电机较小，电机的固有模态频率都偏低，8阶基本力波的频率已经到达21 923 Hz，对于3 600 r/min的8极9槽电机，由n=60f/p可知，电机基波频率为240 Hz，此前分析的电机低阶力波频率为2f0和4f0，电机固有模态频率2 100 Hz约为9f0，因此不会发生共振，而3阶以上固有频率更大，更不会发生共振。

在每个齿上分别均匀取5个点，用相同的方法得到每个点的磁拉力密度，耦合到ANSYS结构分析中，得到电机的三维振动图，然后可以观测具体某点随时间变化振动的位移图像，然后验证其改变措施后振动位移是否减小。

绘制电机定子及机壳，在机壳打4个孔作为固定端，将定子齿上的力耦合，得到电机的位移图像，取其中的一个节点观察其X，Y方向振动位移。

电机转速3 600 r/min，所以电机转一周需16.7 ms，8极有4个电周期，得到图15所示电机机壳表面一点随时间的变化的振动位移图像。传统方法总结起来就是用有限元软件在每个齿的表面取若干个离散的点，计算出每点关于时间的径向力，然后将每个点关于时间的函数以压强的形式加载到电机齿上，从而可以观测电机的振动情况。但这种传统方法有如下缺点：

(a) 电机定子及机壳剖分图

(b)X方向机壳表面的位移(c)Y方向机壳表面的位移

图15 电机的时域响应

1)传统方法只考虑径向力，而没有考虑切向力，切向力方向与电磁转矩方向相反，会使定子齿产生局部变形，从而影响振动。

2)传统方法用离散点代替实际的力波，结果和离散点选取的个数有很大关系。

3)本文电机中有9个齿，每个齿选取5个离散点，需要45次计算，操作非常繁琐。如果对于槽数多的电机，传统方法的工作量将非常大。

而采用磁固耦合，即将有限元磁场力波计算与频谱响应进行联合仿真规避了传统方法的缺点。磁固耦合可以自动将计算出的电磁力(径向、切向)施加在定子齿部，读取电机任何一点的以及电机整体的振动位移频谱响应，从而更加清晰精确地了解电机振动特性。

图16是Maxwell电磁分析与频谱响应分析联合仿真框图。

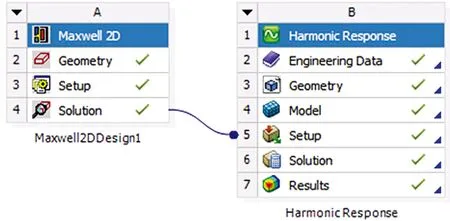
图16 磁固耦合框图

对于定子形状的设计，仅进行振形和结构分析是不够的，具体施加多大的激励，得到多少响应还得借助频谱分析。频谱可以确定电机随电磁力波的加载而得到的稳态响应。可以计算电机在几种不同的频率下的振动位移响应，得到电机振动位移随频率变化的曲线，从而预测电机的持续动力特性，验证电机是否能够克服疲劳、共振以及其它受迫振动。

如图17所示，在定子表面设置A，B，C，D4个观测点。以及电机定子齿和电机轭的内部设置1，2两个观测点。用联合仿真观测各个点振动位移的频谱响应。

图17中A，C和B，D分别空间对称，所以受力相似，位移频谱图也基本重合，如图18所示。。

观测1，2两点的频谱响应图像，可以更好地了解电机内部的振动情况，如图19所示。

图18 定子表面A，B，C，D位移的频谱响应

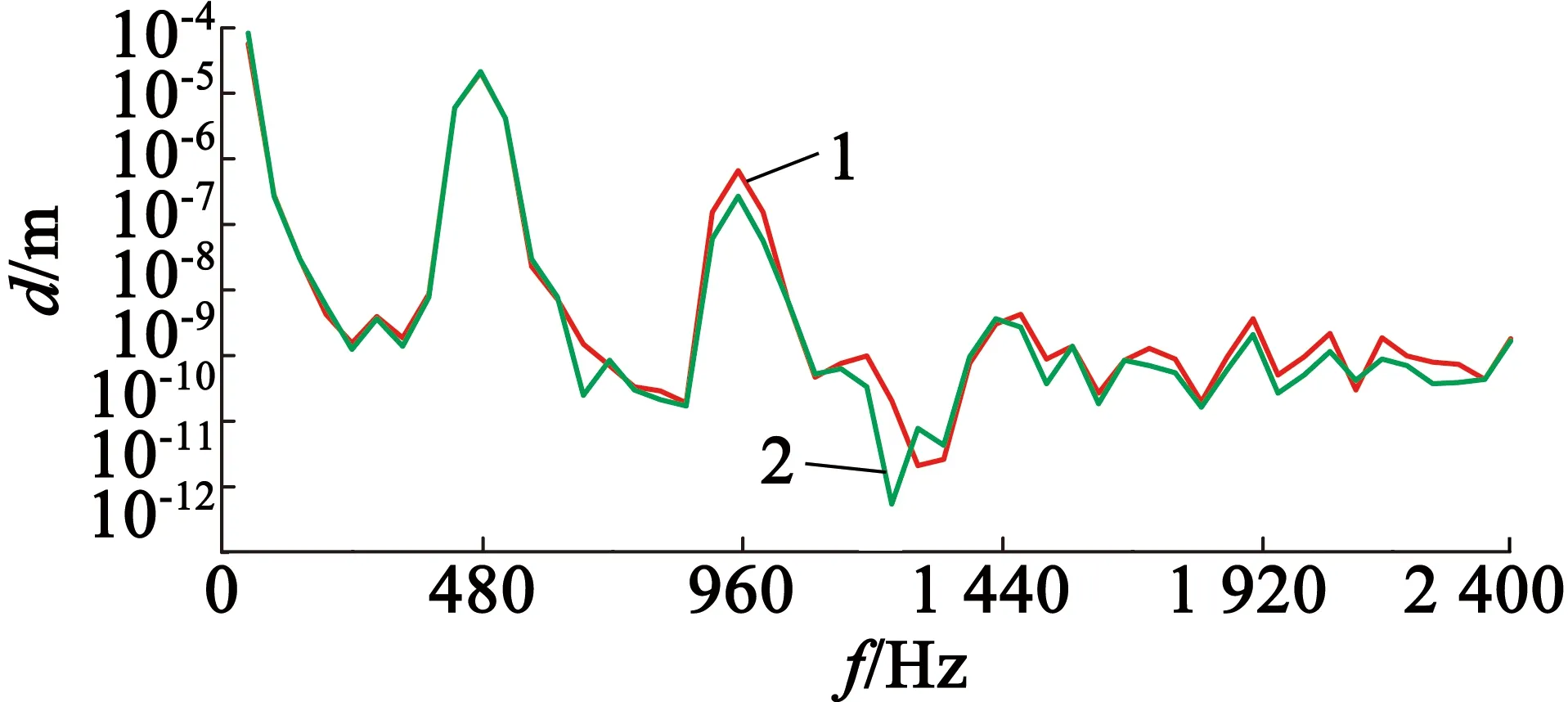
图19 定子内部点1，2位移的频谱响应

以电机基波频率f0=240 Hz为步长，观测电机各点位移的频谱响应，观察图像两个位移最大的点出现在480 Hz，960 Hz处，分别对应的频率为2f0，4f0，即对应的1阶2阶等低阶力波频率，验证了上述的理论分析。定子2阶固有模态频率为2 100 Hz，而2阶力波频率为2f0，4f0，远没有达到2 100 Hz。故不会发生共振，而小电机高阶固有模态频率很高，激振力波频率更不可能达到其共振频率。电机机械结构设计合理。

磁固耦合可以直接生成电机各点在不同频率下的振动位移响应，不仅可以得到电机表面的频谱图，还可以得到电机内部各点的频谱图，这是实际传感器无法做到的，为电机的机械设计阶段提供了有效的实验依据。

5 结 语

奇数槽永磁同步电动机容易产生低阶力波从而引起较大的振动，所以一般在振动要求高的场合尽量避免采用。可以通过开辅助槽的方式有效地减小振动，因为开辅助槽相当于改变槽极配合，但对于小电机容易引起齿部饱和，导致电机发热严重。根据振动位移公式可知，还可以通过加厚定子轭部的方法减小振动，通过改变永磁体的充磁方向，改变磁极形状，使得气隙中谐波含量尽量小，选用等半径式平行充磁磁极形状较好。本文通过对电机定子的模态分析得出小型电机固有模态频率很高，一般情况下不会与激振力波发生共振。用磁固耦合的方法自动将有限元计算出的电磁力波加载电机进行频谱分析，得到电机定子各点随频率变化的频谱图，从而得到电机整体频谱特性，为合理选择电机转速，验证电机结构的合理性提供依据。

[1] 陈益广，潘玉玲，贺鑫.永磁同步电动机分数槽集中绕组磁动势[J].电工技术学报，2010，25(10): 30-36.

[2] 杨浩东,陈阳生,邓志奇.永磁同步电动机常用齿槽配合的电磁振动[J].电工技术学报,2011,26(9):24-30.

[3] 杨浩东,陈阳生.分数槽永磁同步电动机电磁振动的分析与抑制[J]. 中国电机工程学报, 2011,31(24):83-89.

[4] 张冉,王秀和,乔东伟,等.基于辅助槽的永磁电机激振力波削弱方法[J].中国电机工程学报,2010，30(18):103-108.

[5] 刘景辉,黄开胜,陈治宇,等.永磁同步电动机径向电磁力的分析[J].微特电机,2013,41(5):16-18,22.

[6] 蒋晓东.基于气隙电磁力的六相永磁同步电动机振动噪声研究[D].沈阳：沈阳工业大学，2014.

[7] 刘海龙.大型感应电动机电磁力及振动特性分析[D].沈阳：沈阳工业大学，2007.

[8] EL-REFAIE A M.Fractional-slot concentrated-windings synchronous permanent magnet machines: opportunities and challenges[J]. IEEE Transactions on Industrial Electronic,2010,57(1):107-121.

[9] 何鹄环.永磁有刷直流电动机电磁振动与噪声的分析[D].上海：上海交通大学，2012.

[10] YANG H,HAN Z,CHEN Y.Electromagnetic vibration of interior permanent magnet brushless motors under brushless DC and AC operation[C]//International Conference on Electrical Machines and Systems,ICEMS 2009.IEEE,2009:1-6.

[11] 张冉.表面式永磁电机电磁激振力波及其抑制措施研究[D].济南：山东大学，2011.

[12] CHEN Yangsheng,YANG Haodong,HAN Zeying.Investigation of electromagnetic vibration of permanent magnet brushless machines[C]//International Conference on Electrical Machines and Systems,ICEMS 2008.IEEE,2008:621-626.

[13] ZHU Z Q,ISHAK D,HOWE D,et al.Unbalanced magnetic forces in permanent-magnet brushless machines with diametrically asymmetric phase windings[J].IEEE Transactions on Industry Applications,2007,43(6):1544-1553.

[14] WANG J,XIA Z P,LONG S A,et al.Radial force density and vibration characteristics of modular permanent magnet brushless AC machine[J].IEE Proceedings-Electric Power Applications,2006,153(6):793-801.

Investigation on Coupled Magnetical and Solid Vibration of Permanent Magnet Synchronous Motor with Fractional Slot Winding

ZUOJia,GUOYao-xian,QUANXin

(Tianjin University,Tianjin 300072,China)

The structure of small fraction slot permanent magnet motor was optimized in many ways by analyzing the theory of electromagnetic vibration. The calculated electromagnetic force was discretized into points and loaded onto the stator. Eventually the real-time response of stator to dynamic load was obtained by doing transient dynamic analysis in ANSYS. But transient dynamic analysis can only obtain the real-time response of the motor on a certain point instead of the whole motor. However, the calculated electromagnetic force can be automatically coupled to the stator tooth to do spectral by using the magnetic solid coupling joint simulation, thus the spectrum characteristics of the whole motor can be obtained. The simulation results show that using magnetic solid coupling method is more accurate to reflect the spectrum response characteristics of the motor and can be used to guide the design and optimization of the motor structure.

PMSM with fractional slot winding; spectrum analysis; coupled magnetical and solid vibration; motor vibration

2016-01-05

TM341;TM351

A

1004-7018(2016)08-0040-05

左佳(1990-)，男，硕士研究生，研究方向为永磁同步电动机设计与控制。