双珍珠圆梯图的亏格分布

曾建初

(1.昆明理工大学 公共基础设施研究所, 云南 昆明 650093;2.昆明理工大学 学报编辑部,云南 昆明 650500)



双珍珠圆梯图的亏格分布

曾建初1，2*

(1.昆明理工大学 公共基础设施研究所, 云南 昆明 650093;2.昆明理工大学 学报编辑部,云南 昆明 650500)

以联树模型为基础,以一般梯图可定向亏格分布的计算方法为指导,计算了双珍珠圆梯图的可定向亏格分布.

联树模型; 可定向亏格分布; 双珍珠圆梯图

计算图的亏格分布问题是拓扑图论中的一个热点领域.研究图的亏格分布,形成了多种多样的数学方法. 刘彦佩教授是中国拓扑图论领域的鼻祖,他计算图的亏格分布,主要应用联树模型[1].Mohar是美国拓扑图论领域的领头羊,他计算图的亏格分布,主要应用矩阵模型[9]. Mohar在[9]中引用了刘教授课题组的11篇论文,其中包括了[3].本文以联树模型[1，2]为数学工具,受[1～10]思想的启发,改进了[3]中的一个结果,计算了双珍珠圆梯图——一类新的3-正则图的亏格分布. 没有特别说明,本文所说的亏格分布都是可定向的.

1 预备知识

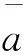
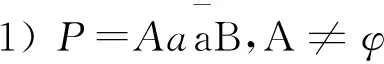
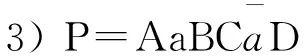
引理1[1]设A,B,C,D,E是多边形P的带符号的线性表示,则

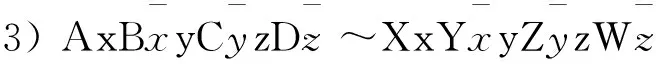
任何一个曲面,其多边形表示都有唯一的一个标准形式:

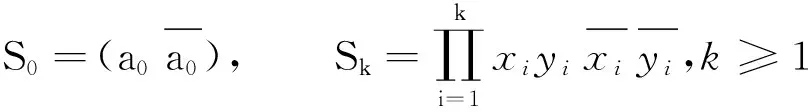
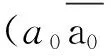
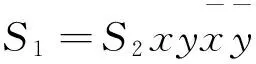
曲面S上的一个同胚f:G→S叫做图G在曲面S上的一个嵌入,其中S-f(G)的每一个分支同胚于一个开圆盘.当且仅当,存在同胚h:S→S,使得f=gh, 我们说两个嵌入f:G→S和g:G→S相等.

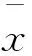
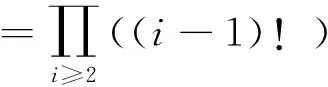
引理4[1]图G在亏格为p的曲面上嵌入的数目,与树T的选取无关.

2 主要结果

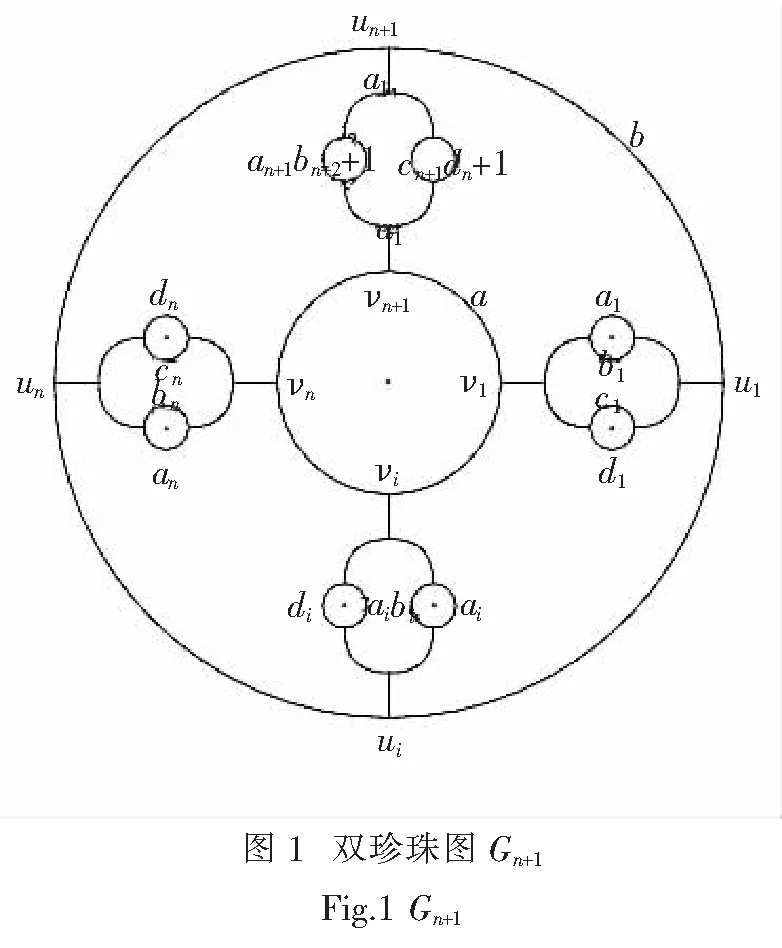
把一个圆梯的每一条梯边从中剖开,嵌入2个圆,这样所形成的图形叫做双珍珠圆梯图,图1是n+1条梯边的双珍珠圆梯图,记为Gn+1.Jn是图Gn+1的一个联树.

根据联树Jn,我们有

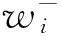
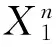
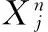
表1 与之间关系表

在[3]中，我们总结了24类曲面.引入如下3个映射ψi(i=1,2,3)[2]:

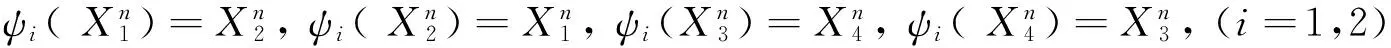
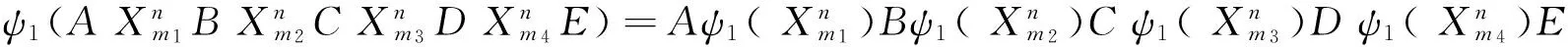
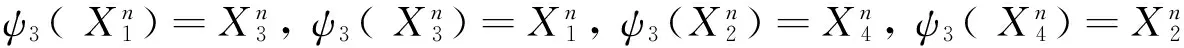
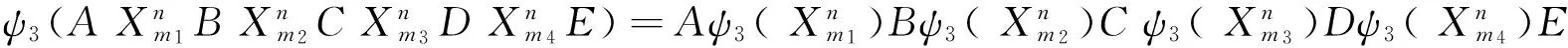
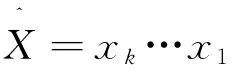
我们能够把双珍珠圆梯图的24类关联曲面化简为下面11类(a,b,c是不同的符号)：

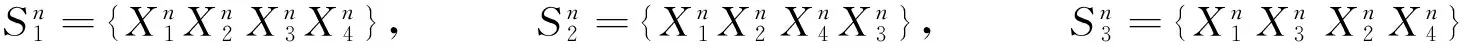
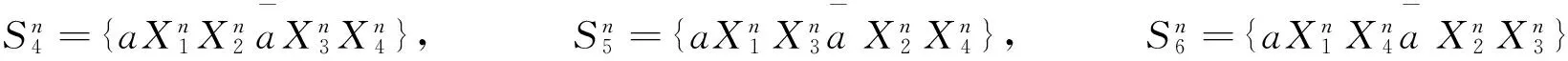
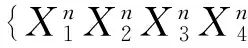
[3]中的24类曲面与本文中11类曲面的对应关系为：

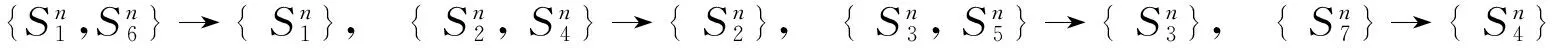
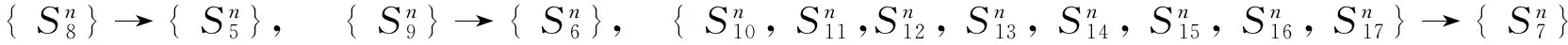
对应于[3]中定理2.1,我们得到定理1.

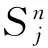
经过计算,我们获得当n=1时，Si(i=1,2,…,11)的亏格的初始值

i1234567891011g0i(1)32323201616160880g1i(1)1601601606411211211264888864g2i(1)6464641921288128128192160160192

定理2 双珍珠圆梯图Gn+1的联树对应的关联曲面是下面的28=256类:

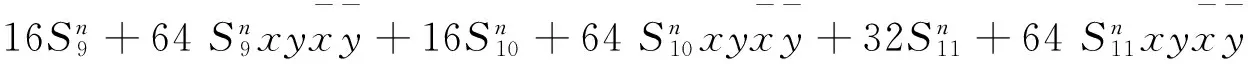
双珍珠圆梯图Gn+1的亏格多项式是:

fGn+1(x)=C0+C1x+C2x2+…+C2nx2n+C2n+1x2n+1,

其中:C0=16g09(n)+ 16g010(n)+ 32g011(n),C1=16g19(n)+ 16g110(n)+ 32g111(n)+ 64g09(n)+ 64g010(n)+ 64g011(n), …, C2n=16g(2n)9(n)+ 16g(2n)10(n)+ 32g(2n)11(n)+ 64g(2n-1)9(n)+ 64g(2n-1)10(n)+ 64g(2n-1)11(n), C2n+1=64g(2n)9(n)+ 64g(2n)10(n)+ 64g(2n)11(n).

当n=1时, C0=256,C1=5 888,C2=26 624，C3=32 768，fG2(x)=256+5 888x+26 624x2+32 768x3.

当n=2时,C0=1 024，C1=56 320，C2=745 472，C3=3 653 632，C4=7 340 032，C5=4 980 736，fG3(x)=1 024+56 320x+745 472x2+3 653 632x3+7 340 032x4+4 980 736x5.

[1] LIU Y P. Theory of polyhedra[M]. Beijing:Science Press,2007.

[2] 万良霞. 一般梯图的亏格分布[J]. 应用数学学报,2008,31(5):806-816.

[3] ZENG J C,LIU Y P. Genus distributions for double pearl-ladder graphs[J]. Ars Combinatorial, 2011,98:511-520.

[4] 刘彦佩. 我所认识的拓扑图论(Ⅰ):球面上十部曲[J]. 昆明理工大学学报(自然科学版),2013(1):105-108.

[5] 任韩.曲面上图染色综述(上)[J].昆明理工大学学报(自然科学版),2016,41(1):130-148.

[6] 吴跃生. 非连通并图I(K_(m,n))∪G的优美标号[J]. 昆明理工大学学报(自然科学版),2015,40(2):142-146.

[7] 谭秋月. 若干图类的平衡指标集[J]. 昆明理工大学学报(自然科学版),2014,39(6):136-140.

[8] 于海峡,龙顺潮.n维分数次Hardy算子与它的对偶算子的端点估计(英)[J]. 湘潭大学学报(自然科学版), 2015(2):10-15.

[9] Bojan Mohar. The Genus Distribution of Doubly Hexagonal Chains[EB/OL]. arXiv[math.CO]: 1505. 03664 vl,2015.

[10] 马京成,马登举,朱珺. 3-正则Halin图的完美匹配数[J].昆明理工大学学报(自然科学版),2015,40(5):132-136.

责任编辑：龙顺潮

Genus Distribution of Double Zhenzhuyuan Ladder

ZENGJian-chu1，2*

(1. Institute of Infrastructure Project Management， Kunming University of Science and Technology, Kunming 650093; 2.Editorial Department of Journal， Kunming University of Science and Technology, Kunming 650500 China)

Based on joint tree model, with the guidance of the calculation method orientable genus distribution of general ladder,the paper calculates orientable genus distribution of double zhenzhuyuan ladder.

joint tree model; orientable genus distribution; double zhenzhuyuan ladder

2016-01-01

云南省人才培养项目(KKSY201213063).

曾建初(1964-),男,湖南 涟源人,博士,副教授.E-mail:kgxb08@163.com

O157.5

A

1000-5900(2016)02-0001-04