渗透对均质无黏性土坝溃坝的影响分析

王洪洋 娄浩然

(北京工业大学，北京 100124)



渗透对均质无黏性土坝溃坝的影响分析

王洪洋 娄浩然

(北京工业大学，北京 100124)

利用离散单元法，并考虑流固耦合作用，通过设定不同的边界水压力，研究了均质无黏性土坝溃坝过程中的渗流和冲刷现象，结果表明：当边界水压力较小时，溃坝主要由表面流冲刷引起；随着边界水压力增大，溃坝同时由渗流和漫顶两部分水流引起。

土石坝，溃坝，离散元，流固耦合

0 引言

土石坝作为重要的水工构筑物，给人类带来了巨大的经济效益和社会效益，但是，土石坝也较容易发生溃坝事故。据统计[1]，至2006年年底，我国已有3 280余座土石坝发生溃坝，如河北“63.8”、河南“75.8”暴雨造成数百座水库坝体溃坝，致使大量土地村庄被淹，1 000多万人受灾[2]。资料表明，全世界范围内也发生了大量土石坝溃坝事故，例如美国的琼斯堂大坝、提堂大坝等等。

土石坝溃坝研究涉及土力学、水力学和泥沙动力学多个学科，溃决过程比较复杂，颗粒流软件(PFC)以离散单元法为基本方法，可以模拟非线性、大变形问题，在岩土工程领域已经得到了广泛的应用。Shamy & Aydin[3]利用该软件考虑流固耦合作用，建立了一个饱和的大比尺土石坝模型，对于砂土管涌的临界水力梯度进行了研究，验证了颗粒流软件在大变形条件下模拟水土耦合效应的可行性；周健等[4]结合细观模型试验，利用PFC对砂土管涌的发生发展过程进行了模拟，模拟结果与有关的模型试验较吻合。

由于均质无黏性土坝的渗透系数较大，在遭遇洪水漫顶时，漫溢水流一部分冲刷坝体表层，一部分则渗进坝体内部，对坝身造成渗流冲刷。本文利用颗粒流软件研究均质无黏性土坝溃坝，通过实时监测坝体内部孔隙率、孔隙水压力等物理量的变化，研究渗流和冲刷对土石坝溃坝的影响。

1 颗粒流方法简介

三维颗粒流方法以球体为基本单元，通过定义球体直径、球体刚度和黏结强度等细观参数表征宏观土体的物理性质。颗粒运动符合牛顿第二定律，流体采用固定的粗网格划分方法，利用SIMPLE方法求解。

流体质量和动量守恒方程如下：

(1)

(2)

牛顿流体的本构方程为：

(3)

联立式(1)～式(3)得到广义的N-S方程：

(4)

式中：n——孔隙率；

u——流体速度；

nu——达西流速；

ρf——流体密度；

Ff——体积力；

p——压强；

τij——摩擦剪应力；

μ——动力粘滞系数。

颗粒流软件通过求解广义N-S方程，实现流体和固体颗粒的耦合迭代过程。

2 土石坝三维颗粒流模型

利用均质无黏性土坝的对称性，选取坝体的1/4建立数值模型，以提高计算效率和收敛速率，如图1所示。初始生成的长方体模型首先在自重作用下平衡(不平衡力很小)，然后用削坡的方法制备土坝模型，模型尺寸为25 mm×50 mm×25 mm(高×长×宽)。颗粒粒径为0.35 mm～0.58 mm，颗粒总数为4 764个，其余参数见表1。在土坝模型中部靠近坝坡的位置设置测量圈，监测孔隙率、孔隙水压力的变化，每1 000步记录一次数据。

对土坝模型划分4×10×8的流体网格，每个网格包含若干球体颗粒，流体压力以体力的形式作用于颗粒，改变球颗粒的运动状态，球体颗粒反过来又影响流体的运动过程。

表1 颗粒流模型细观参数表

3 模拟结果分析

3.1 坝坡冲刷过程

以P=634 Pa为例，分析均质无黏性土坝的溃坝过程，如图2所示。在漫顶冲刷前期，单个颗粒受到流体的拖拽剪应力，失去平衡状态，开始自坝坡的不同位置以滚动的形式下落，到155 000步时，坡脚的颗粒呈团状脱离坝体，这种现象和室内模型试验结果一致，在模型试验中，土坝遭遇漫顶洪水时，首先被冲刷的部位即是下游坡脚。随着颗粒团状流失，冲刷速率加大，310 000步时，下游坝坡靠近坝顶的颗粒在流体压力和重力的共同作用下达到极限平衡状态，沿着破裂面滑动，滑坡体在坝坡表面形成不连续的凸起，到465 000步时坝坡才重新变得光滑。由于被冲刷的颗粒很多集中堆积在坡脚，使得靠近坝基的土坝模型冲刷较慢，而坝体上部的冲刷速率仍然很大，随着冲刷的进行，坝顶逐渐变窄，到620 000步时，靠近坝顶位置的坝坡又再次发生失稳滑落。

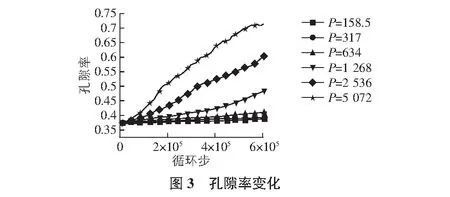
3.2 坝坡孔隙率变化

不同边界水压力下测量圈内的孔隙率变化如图3所示。由图3可知，初始孔隙率为0.371，在六种边界水压力作用下，靠近坝坡位置的孔隙率随着循环步数的增加而增大，但增大的速率不同。当边界水压力为158.5 Pa，317 Pa和634 Pa时，在620 000循环步内，孔隙率变为0.387，0.391和0.411，只分别增加了4.3%，5.4%和10.7%；而当边界水压力为1 268 Pa时，孔隙率在400 000步时明显增大，最后的孔隙率为0.487，增长率为31%；随着边界水压力进一步加大，孔隙率的变化速率越来越快，2 536 Pa和5 072 Pa最终的孔隙率分别为0.603和0.712，相应增加了62.5%和92%。

3.3 坝坡孔隙水压力变化

图4a)是边界水压力为634 Pa时的孔隙水压力变化曲线，由于初始阶段的应力重分布，孔隙水压力快速下降，出现负孔压，大约在70 000步时，孔隙水压力到达平衡值-40 Pa，此后一直保持该值不变。这说明，在均质无黏性土坝溃坝初期，土颗粒受到挤压

作用，孔隙水压力值为正，而随着坝体材料被流体冲散，压实度降低，孔隙率增加，出现体积膨胀，孔隙水压力变为负值。图4b)为不同边界水压力时，平衡孔隙水压力的变化曲线，由图4可知，边界水压力分别为158.5 Pa，317 Pa，634 Pa，1 268 Pa，2 536 Pa和5 072 Pa时，平衡孔隙水压力分别为8.3 Pa，-18 Pa，-40 Pa，-60 Pa，-130 Pa和-450 Pa，随着边界水压力增大，孔隙水压力的平衡值增加。以上的分析说明：当渗透性较大的土石坝发生漫顶溃坝时，漫顶水流压力较小时，坝内孔隙率变化量和平衡孔隙水压力值很小，此时的溃坝主要由表面流冲刷引起；反之，当漫顶水流压力较大时，坝内孔隙率变化量和平衡孔隙水压力值都很大，此时的溃坝现象由渗流和漫顶两部分水流造成。

4 结语

建立均质无黏性土坝的离散模型，在坝顶施加不同的水压力值，研究渗透和冲刷对土坝溃坝的影响。结果表明：当漫顶水流很浅，水压力很小时，渗流对土坝溃坝的影响很小；而当漫顶水流较深，水压力较大时，渗流对土坝溃坝的影响不可忽略。

[1] 解家毕，孙东亚.全国水库溃坝统计及溃坝原因分析[J].水利水电技术，2009(12):124-127.

[2] 汝乃华，牛运光.大坝事故与安全——土石坝[M].北京：中国水利水电出版社，2001.

[3] U.EI Shamy,F.Aydin.A micro-scale model for the analysis of flood-induced piping in river levees.Embankments,Dams,and Slopes.ASCE,2007.

[4] 周 健，周凯敏.砂土管涌—滤层防治的离散元数值模拟[J].水利学报，2010，41(1):17-24.

Influential analysis of penetration upon homogeneous non-viscous earth dam break

Wang Hongyang Lou Haoran

(BeijingUniversityofIndustry,Beijing100124,China)

Applying discrete element method, taking flow-solid coupling into consideration, through setting different boundary water pressure, the paper studies penetration and scouring phenomena occurring homogeneous non-viscous earth dam break process. Results show that: when the boundary water pressure is smaller, the dam break is mainly caused by surface scouring, with the boundary water pressure increasing, the dam break is mainly caused by penetration and overtopping water flow.

earth-rockfill dam, dam break, discrete element, flow-solid coupling

1009-6825(2016)13-0221-02

2016-02-21

王洪洋(1993- )，男，在读硕士； 娄浩然(1991- )，男，在读硕士

TV641

A