妙招破解复数探索型试题

■浙江省台州市洪家中学 钭伟炀



妙招破解复数探索型试题

■浙江省台州市洪家中学 钭伟炀

一、条件探索型

条件探索型试题，给出问题的结论，但没有给出或给出题目的部分条件，要求补充出使问题结论成立的条件。解这类题采取的策略是执果索因，首先要从结论出发，考虑结论成立时所要满足的条件，从而得到答案。

例1 已知a、b、c、d∈R，要使关于x的方程x2+(a+bi)x+(c+di)=0有实数根，要对a、b、c、d添加什么条件？并证明你的结论。

分析：可以假设复数系中一元二次方程有实根，应用复数相等的定义转化为实数方程组解决。

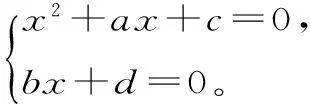
方程①是实数系的一元二次方程，存在实根的条件是a2-4c≥0。

③

方程②存在实根的条件是：

b≠0或b=d=0。

④

当b=d=0且a2-4c≥0时，方程有实数根。

综上所述，要使方程有实数根，对a、b、c、d需添加的条件是：

点评：解条件探索题采用的是“逆向思维”的方法，解此类问题需要同学们有扎实的基本功及灵活处理问题的能力。

二、结论探索型

结论探索型试题，这类问题的基本特征是给出条件而无结论或结论的正确与否需要确定。解这类问题通常先假定其结论存在，再进行计算、推理，如果能推导出符合条件的结论，则表示结论存在；若推出相矛盾的结论，则结论就不存在。

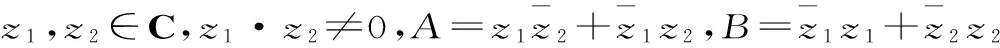
分析：只需判断A、B是否都是实数，若是实数，就可以比较大小；只要有一个不是实数，就不能比较大小。

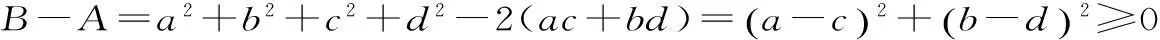
点评:本题要求找到两个数的关系，并说明理由，对思维能力要求较高，突出了对探索、归纳、推理能力的考查。

三、存在探索型

存在探索型试题，是指在确定的条件下判断某个数学对象是否存在。解决这类问题的策略是先假设需要探索的对象存在，从条件和假设出发进行运算、推理。若出现矛盾，则不存在；若不出现矛盾，则肯定存在。

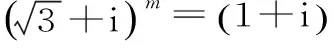
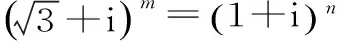
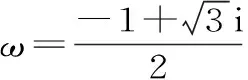
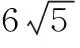
点评：此题采用了先假设再求解的方法，即“先假设存在—演绎推理—得出结论”。

(责任编辑 徐利杰)