推理与证明必考题型赏析



推理与证明必考题型赏析

■辽宁省盖州市第一高级中学 李 闯

一、归纳推理中注意结构特征和项数的变化规律

正方形数N(n,4)=n2；

六边形数N(n,6)=2n2-n；

……

可以推测N(n,k)的表达式，由此计算N(10,24)=____。

点评：归纳是依据特殊现象推断出一般现象，因而由归纳所得的结论超越了前提所包含的范围。一般而言，是抓住“n”进行观察，尤其要“看透”等式左边和式(或积式)中的最末一项，有的需要挖掘隐含条件，有的需要变形，有的需要辅以计算。如本题构造等差数列{ak}，{bk}的通项公式得到N(n,k)的一般规律。

二、类比推理中注意形式和方法的类比

图1

解析：在Rt△ABC中，由AB⊥AC,AD⊥BC,可得AB2=BD·BC,AC2=CD·BC,AD2=BD·CD。

图2

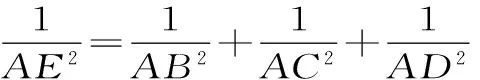
连接BE并延长交CD于点F，连接AF。

因为AB⊥AC,AB⊥AD，AC与AD同在平面ACD内，且AC∩AD=A，所以AB⊥平面ACD。

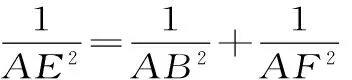
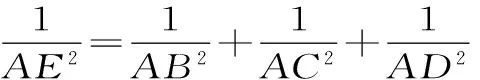
点评：在进行类比推理时，不仅要注意形式的类比，方法的类比，还要注意找两类对象的对应元素，找对应元素的对应关系。

三、新定义推理中注重演绎推理

解析：新定义的函数利用三点共线的条件探究其特殊性，再得到特殊函数的表达式。

设A(a，f(a))，B(b，-f(b))，C(c，0)，则此三点共线。

点评：依据新定义和三点共线的条件，探究三点的坐标满足的关系式，抽象概括出特殊函数的表达式，本题系典型的演绎推理。大前提为定义函数f(x)的平均数，利用三点共线进行推理构造满足条件的特殊函数，对同学们综合解决问题的能力要求较高。

四、分析法证明中注意书写格式的规范

点评：分析法的证明思路：先从结论入手，由此逐步推出保证此结论成立的充分条件，而当这些判断恰恰都是已证的命题(定义、公理、定理、法则、公式等)或要证的命题的已知条件时命题已得证。 要注意书写格式的规范性。

五、反证法证题否定结论一定要推出与题设或结论明显的矛盾

例5 已知长、宽、高分别为a、b、c的长方体的表面积为24，求证：a、b、c至少有一个不小于2。

分析：证明的第一步是作出否定结论的假设，“a、b、c至少有一个不小于2”亦即“a、b、c至少有一个大于等于2”，它包括三种情形：“a、b、c只有一个大于等于2”，“a、b、c有两个大于等于2”，“a、b、c都大于等于2”，所以它的否定应为“a、b、c都小于2”。证明的第二步是以“a、b、c都小于2”为基础，运用数学知识和已知条件进行推理，直至导出矛盾。 证明的第三步是根据相关逻辑知识说明原命题是真命题，从而问题得证。

证明： 假设a、b、c都小于2，则a2+b2+c2<12。

因为a2+b2≥2ab,b2+c2≥2bc,a2+c2≥2ac，三式相加得2(a2+b2+c2)≥2ab+2bc+2ac=24，所以a2+b2+c2≥12，这与a2+b2+c2<12矛盾。

所以，a、b、c不可能都小于2，其中至少有一个不小于2。

点评：先否定命题的结论，而承认命题的条件，经过推理后，与假设相矛盾，从而得出原命题为真命题。

六、数学归纳法证明数列问题一定要用归纳假设和数列本身的特征

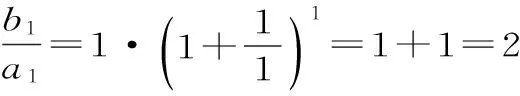
下面用数学归纳法证明(*)式成立。

(1)当n=1时，左边=右边，(*)式成立。

=(k+2)k+1。

所以当n=k+1时，(*)式也成立。

根据(1)(2)，可知(*)式对一切正整数n都成立。

七、题目中含有“不可能”时，常用反证法

(1)求数列{an}，{bn}的通项公式；

(2)证明:数列{bn}中的任意三项不可能成等差数列。

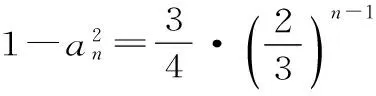
因此只可能有2bs=br+bt成立。

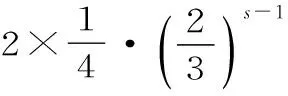
化简得3t-r+2t-r=2·2s-r·3t-s。(*)

因为r

点评：反证法先否定命题的结论，而承认命题的条件，经过推理后，发现与假设或结论有明显的矛盾，进而得到原命题为真命题。 当一个命题的结论是以“至多”、“至少”、“唯一”或以否定形式出现时，宜用反证法来证，反证法的关键是在正确的推理下得出矛盾。

八、立体几何推理中注重演绎推理

例8 (2015年山东高考理17)如图3，在三棱台DEF-ABC中，AB=2DE,G,H分别为AC,BC的中点。

图3

(1)求证：BD∥平面FGH；

(2)如果CF⊥平面ABC，AB⊥BC,CF=DE，∠BAC=45°,求平面FGH与平面ACFD所成的角(锐角)的大小。

解析：(1)可构造辅助面为平行四边形以及三角形的中位线得到线线平行，进而求证线面平行。连接DG,CD，设CD∩GF=O。连接OH，在三棱台DEF-ABC中，由AB=2DE,G为AC的中点，可得DF∥GC,DF=GC，所以四边形DFCG为平行四边形，则O为CD的中点。

又H为BC的中点，所以OH∥BD。

又OH⊂平面FGH,BD⊄平面FGH, 所以BD∥平面FGH。

(2) 由CF⊥平面ABC，如图4所示，易知平面ABC⊥ACFD。

作HM⊥AC于点M，设AB=2，则CF=DE=1。作MN⊥GF于点N，连接NH。

图4

由FC⊥平面ABC，得HM⊥FC。

又FC∩AC=C，所以HM⊥平面ACFD。

又NM⊥GF,因此GF⊥NH,∠MNH即为所求二面角的平面角。

所以平面FGH与平面ACFD所成角(锐角)的大小为60°。

点评：立体几何问题的求解过程系演绎推理的三段论模式，大前提为空间中的定义、定理和结论，一定正确，小前提是所研究的特殊情况(面面垂直、线面平行和体积计算等)，根据一般原理，对特殊情况作出的结论一定正确。要正确认识演绎推理的特点，把握三段论思想的具体应用，提高自身的逻辑推理能力。

(责任编辑 徐利杰)