数学思想在《推理与证明》中的运用

■江苏省盐城市时杨中学 刘长柏



数学思想在《推理与证明》中的运用

■江苏省盐城市时杨中学 刘长柏

一、类比思想

所谓类比思想就是根据两个对象之间一部分属性相同或相似，从而推断出这两个对象之间的另外一些属性也可能相同或相似的一种思维形式。“由特殊到一般”是解决这类问题的思维主线。

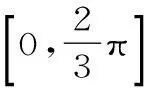
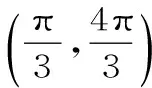
图1

图2

图3

点评：本题考查同学们利用新结论解决问题的能力，灵活运用数形结合思想及类比推理是解题的关键。类比的方法主要有：概念之间的类比，与已知数学方法的类比，与已知结论的类比等。作为一种创新题型，类比推理已成为近年高考命题中的一个亮点。

二、归纳思想

归纳思想就是在解决问题时，从特殊情况入手，通过观察、分析、概括，猜想出一般性结论，然后用演绎推理对结论进行证明。这种数学思想方法在解决探索性问题、存在性问题或与正整数有关的命题时有着广泛的应用。思维模式是“观察—归纳—猜想—证明”，解题的关键是正确地归纳猜想。

(1)5=2+3，请你推测g(5)能否用f(2),f(3),g(2),g(3)来表示；

(2)如果(1)中获得了一个结论，你能否将其推广？

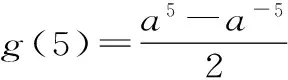
因此，g(5)=f(3)g(2)+g(3)f(2)。

(2)g(5)=f(3)g(2)+g(3)f(2)，也即g(2+3)=f(3)g(2)+g(3)f(2)。

于是推测：

g(x+y)=f(x)g(y)+g(x)f(y)。

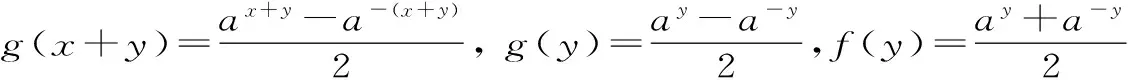
(小前提及结论)

所以f(x)g(y)+g(x)f(y)

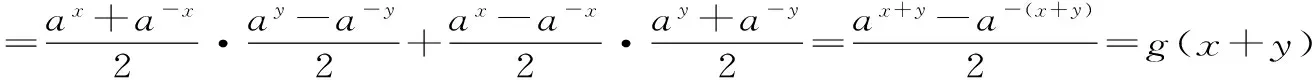
点评：此题是一典型的由特殊到一般的推理，构造g(2+3)=f(3)g(2)+g(3)f(2)是此题的一个难点，要经过观察、分析、比较、联想而得到。从而归纳推出一般结论g(x+y)=f(x)g(y)+g(x)f(y)。特例试验、归纳猜想是理性思维的重要体现，是获得发现的源泉。近年高考特别注重对归纳猜想和由特殊到一般问题的解决方法的考查，主要形式是根据已知条件归纳出一个结论，再用演绎推理对结论进行证明。

三、转化思想

转化思想就是在解决数学问题时，将有待解决的问题，通过转化，使之成为一个已经解决或比较容易解决的问题，并通过对这一问题的解答从而使原问题得到解决。

例3 已知a，b，c是不全相等的正数。

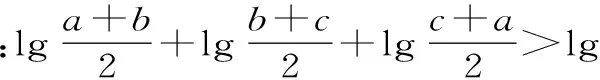
点评：运用分析法解题的关键是将结论适当转化。分析法解题方向较为明确，有利于寻找解题思路；综合法条理清晰，宜于表述。在实际解题时，通常以分析法为主寻求解题思路，再用综合法有条理地表述过程。

四、正难则反思想

有些问题当从正面求解烦琐或无法求解时，可从其反面进行思考，通过否定结论的反面来肯定结论的正确，这就是正难则反的思想。反证法就是“正难则反”的一种证明方法，它不直接证明命题的结论正确，而是通过证明结论的反面不正确来说明结论的正确。因而对于那些“结论的反面”比结论本身更具体、更明确、更简单的命题，则适宜用反证法来证。

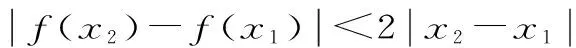
分析：若用直接法，需分类讨论，于是可考虑使用反证法。

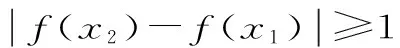
=2x2+2-2x1=2-2(x1-x2)。

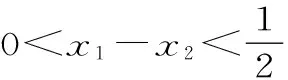
这与假设矛盾，故原命题成立。

(责任编辑 徐利杰)