数学思维的起点——数形结合

吴红伍

（四川省眉山市东坡区山宝中心小学）

数学思维的起点
——数形结合

吴红伍

（四川省眉山市东坡区山宝中心小学）

数学思维，特别是应用题思维，历来就是小学数学教学的重难点；学生在课堂上学懂的知识，在运用时却又茫然失措。究其原因，正如华罗庚所说：“人们对数学早就产生了枯燥无味、神秘难懂的印象，成因之一便是脱离实际。”而“数形结合”就是利用线段图、实物图、列举、列表等特殊的“形”表现实际生产、生活的数量关系。因此，教师应把“数形结合”的方法教给学生，让学生把它作为数学思维的起点。

在实践中，很多教师都已运用了数形结合，并在不断地提高其表现质量（如教具、多媒体等），但大家却往往忽视了把这种方法教给学生。因此，根据“数形结合”的内在特征，教师可以教给学生数形结合的思维方法：一性，二移，三启。

一性：

即“对应性”。通过抓住“数形结合”中“数”与“形”、“数”与“数”的“对应”关系进行分析，思路自然清晰。

例如，将一根木料锯成4段用12分钟，按这样的速度，现要将一根同样大小的长木料锯成7段，需要多少时间？

学生在一般情况下，最容易理解成所需的时间与段数相对应，所以会错误地理解成：12÷4×7=21（分钟）

如果用线段图，则表示为：

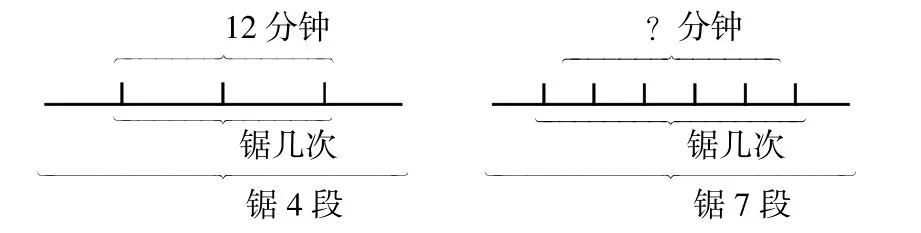
从图中的对应关系可以直观看出，所需的时间并不与所锯的段数相对应，而应与所锯的次数相对应。由此，不难求出每锯一次所需的时间，从而求出锯的次数总比锯的段数少1。因此，正确的列式应为：12÷（4-1）×（7-1）=24（分钟）。

二移：

即转移。在复合应用题中，某些隐藏条件学生难以发现，但是，在“数形结合”中能找到与之对应的“空位”。只要我们抓住这些空位进行思考，求问题就可以转移为求空位。

例如，世界第一大河是南美洲的亚马孙河，全长4480千米，我国长江是世界第三大河，全长仅比亚马孙河短三十六分之一，长江的长是多少千米？

用线段表示：

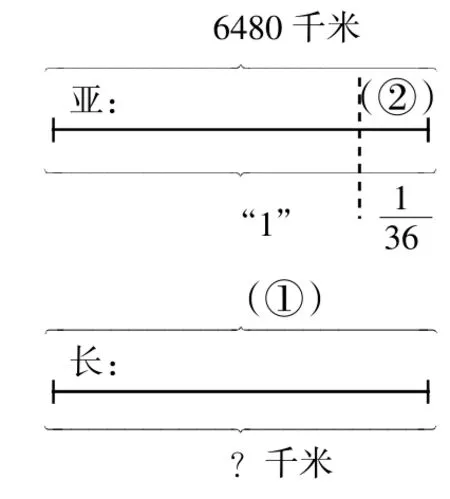
从本题的对应情况来看，则有两处空位①、②出现。如从空位①入手，通过对“形”（即线段）的比较即可转移为对分率的比较，则空位①=（1-，那么，由于问题与①的对应关系，所以问题=6480×（1-）。又如从空位②入手，由于空位②与的对应关系，则空位②=6480×，再通过对“形”（即线段）的比较，得出问题=6480-6480×。

三启：

即启发。抓住“数形结合”的对应性，通过比较分析，转化启发学生的想象思维、逻辑思维和发散思维等。

例如，福光饲养场去年养猪4000头，比前年养猪头数多百分之二十五，去年养猪头数的五分之一等于今年养猪头数的六分之一，今年养猪的头数比前年提高百分之几？

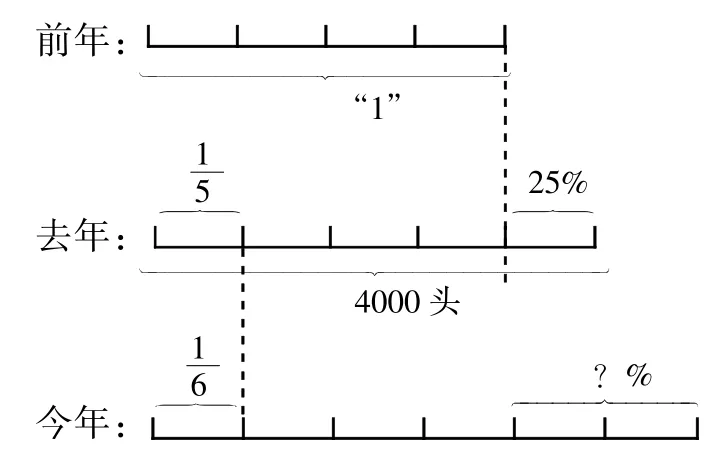
如果按一般的解题思路，应为：

（1）先求前年的养猪头数：4000÷（1+25%）=3200（头）

（3）今年比前年提高百分之几：（4800-3200）÷3200=50%

如果应用“数形结合”就能直接看出：前年、去年与今年的份数比为4：5：6，今年比前年多的百分比为25%×2=50%或2份÷ 4份=50%。

综上所述，当教师教给了学生“数形结合”的思维方法，学生就会借助一张纸、一支笔展现一种不是实物而胜似实物的“形”，他们就会有“形”可视，有“物”可比，有“理”可推，进而提高学生的创造性思维能力。

［1］吴子林.数形结合思想在小学数学中的渗透［J］.学周刊，2014（31）.

［2］金妤茜.浅谈数形结合思想在数学教学中的运用［J］.小学教学参考，2012（32）.

·编辑 杨国蓉