附加黏弹性阻尼器的钢框架结构减震性能研究

魏春彤， 裴星洙

(江苏科技大学 土木工程与建筑学院，江苏 镇江 212000)



附加黏弹性阻尼器的钢框架结构减震性能研究

魏春彤， 裴星洙

(江苏科技大学 土木工程与建筑学院，江苏 镇江 212000)

定义未加黏弹性阻尼器的结构为原结构，附加黏弹性阻尼器的结构为消能减震结构。建立12层钢框架结构模型并计算其恢复力特性，根据原结构以及采用分数微分方法计算的消能减震结构的振动微分方程，分别编制两种结构的弹塑性时程分析程序，计算在多种地震动作用下的地震反应，并对两者的能量分配进行比较分析。对消能减震结构中黏弹性阻尼器的不同布设方式以及投放量进行研究，得出阻尼器投放量与楼层的相关性并进行验证。结果表明，黏弹性阻尼器不仅具有很好的减震效果，而且可以根据阻尼器投放量与楼层的相关性确定阻尼器投放量，使结构的减震效果达到较优的状态。

黏弹性阻尼器；地震反应；能量分配；阻尼器投放量

国内外频繁发生的地震灾害使得建筑结构抗震设计具有十分重大而深远的意义。越来越多的消能减震装置被用于提高结构的抗震性能的工程实例中，其中黏弹性阻尼器因其良好的耗能能力被广泛采用。由于黏弹性材料具有弹性和黏性双重特性，故其能可为结构提供附加刚度和阻尼，即使是在微小干扰下结构的振动，阻尼器也能马上耗能。而且其“恢复力-位移”滞回曲线近似于椭圆形，故相较于其他类型的阻尼器具有很强的耗能能力[1]。

周云等[2]通过对黏弹性阻尼器的性能、疲劳特性和极限变形的试验研究，得出了温度、频率、应变幅值以及黏弹性层厚度对黏弹性阻尼器的影响规律；周颖等[3]根据附加黏弹性阻尼器钢框架结构的振动台试验结果，提出了基于OpenSees的阻尼器尺寸选择方法；以上学者通过试验对结构的动力特性和结构反应进行了对比分析，结果均表明黏弹性阻尼器具有良好的变形性能和耗能能力。

谭小蓉等[4-6]采用有限元软件，如SAP2000，ANSYS等，对附加黏弹性阻尼器的结构进行了模拟研究，得出的结论与上述学者试验研究所得出的结论是吻合的。此外，程文瀼等[7]总结了国内重大工程结构采用黏弹性阻尼器进行抗风减震的典型案例，如宿迁市13层交通大厦等，结果表明结构附加黏弹性阻尼器后不仅能够满足多遇、罕遇水平地震作用下的承载力与变形的要求，甚至可以降低抗震设防要求，且能够降低结构材料用量，节约主体结构的工程造价。

在以上的研究中，几乎没有涉及到减震结构设计初期如何设定阻尼投放量的棘手问题。日本学者笠井和彦[8]提出利用“减震性能曲线”设定阻尼投放量的方法。其方法推导严密、思路清晰，但是应用起来较为麻烦。

本文旨在为附加黏弹性阻尼器的消能减震结构设计，提出更为方便简单的设定阻尼投放量的计算方法，其主要内容是建立12层钢框架结构算例模型，采用自编程序、利用多条地震动对算例模型进行弹塑性时程分析[9]，在多种工况中考察其地震反应的变化规律，得出阻尼器投放量与楼层的关系，并以10层钢框架结构为对象，对所得结果进行了验证。

1 算例模型

某12层钢框架结构，长度为38.4 m，宽度为28.8 m，首层层高为6.0 m，其余各层均为4.0 m，Y方向各跨度均为9.6 m，其结构平面图和立面图如图1、2所示，其构件截面形式和尺寸见表1，梁、柱采用固结方式连接。本文仅讨论Y方向上的地震作用反应，并且仅选择Y方向的一榀框架作为研究对象，每榀计算宽度(柱距)为6.4 m，假设质量均匀分布，其大小为1 000 kg/m2，钢材牌号为Q345，弹性模量为206 GPa。

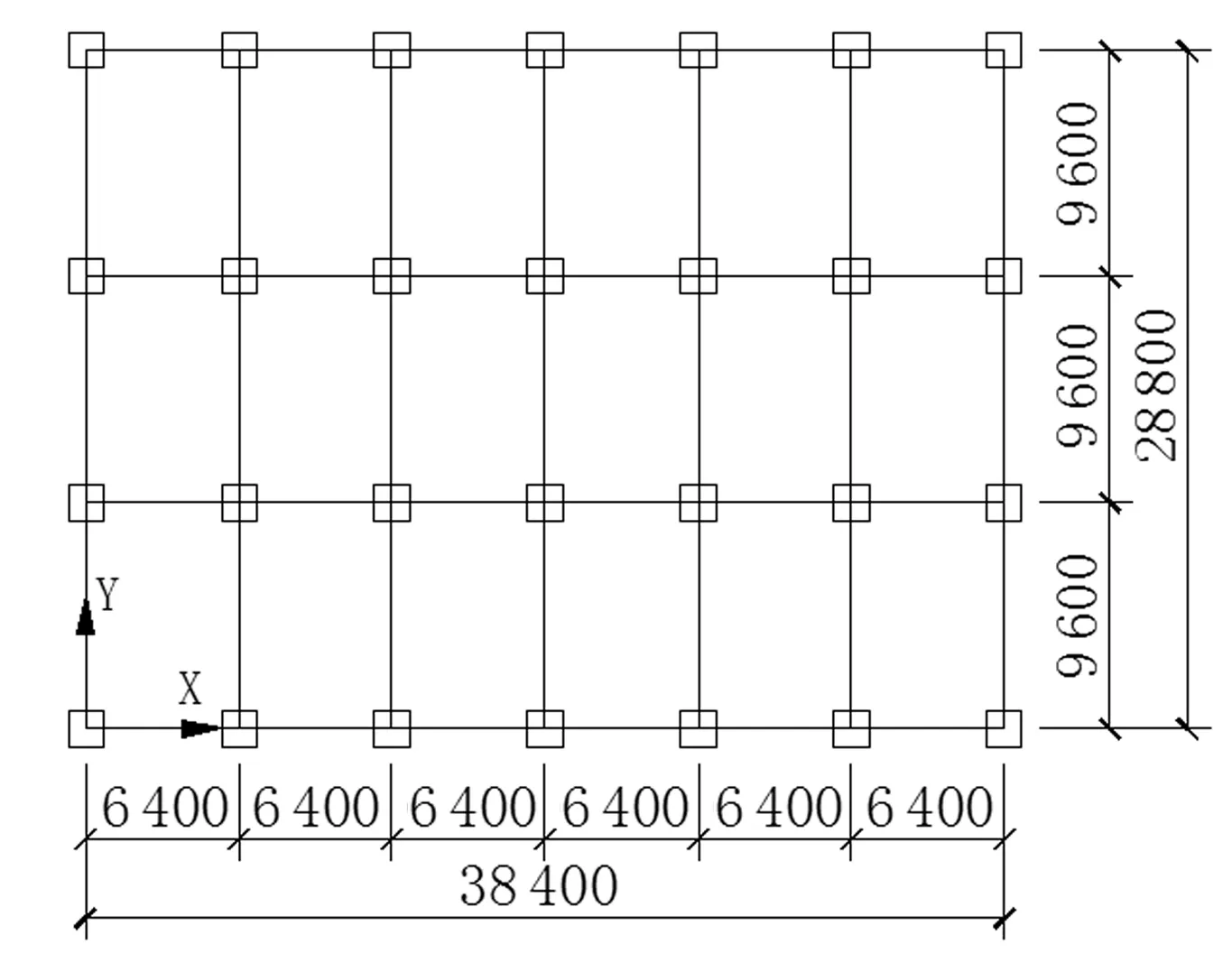
图1 结构平面图Fig.1 Plan of structure

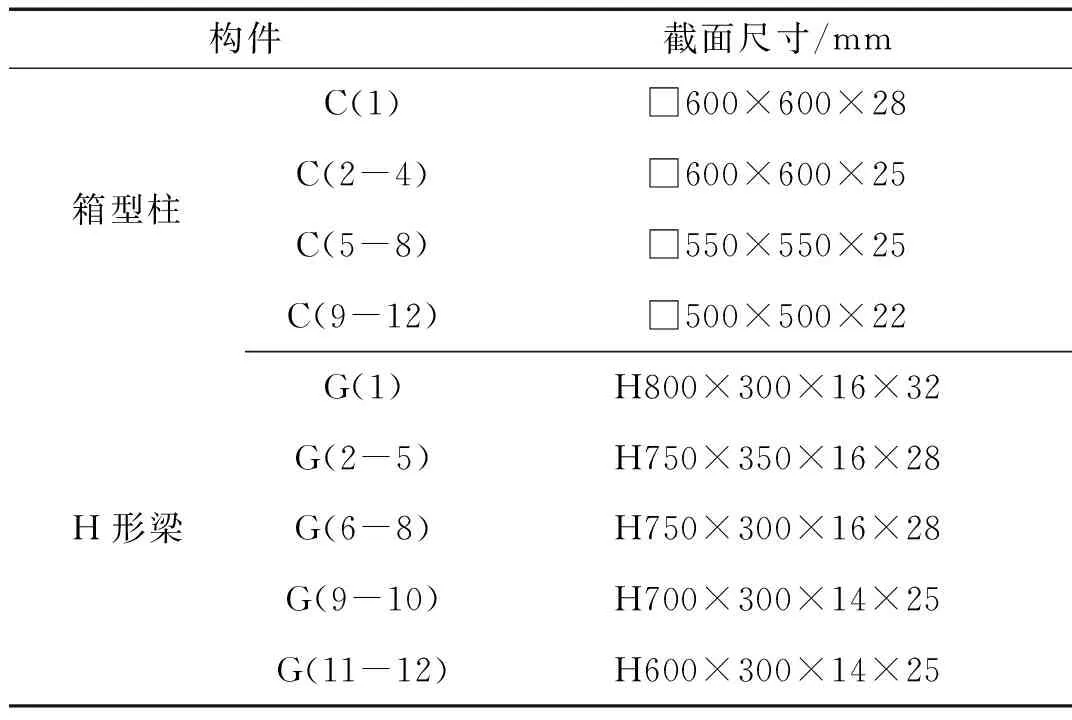
构件截面尺寸/mm箱型柱C(1)□600×600×28C(2-4)□600×600×25C(5-8)□550×550×25C(9-12)□500×500×22H形梁G(1)H800×300×16×32G(2-5)H750×350×16×28G(6-8)H750×300×16×28G(9-10)H700×300×14×25G(11-12)H600×300×14×25

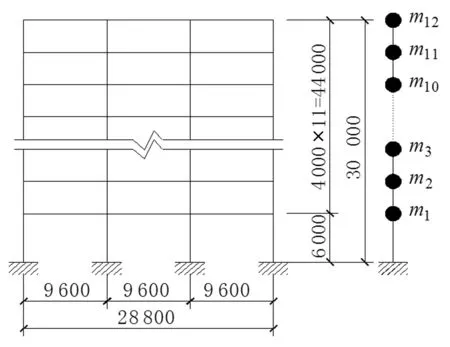
图2 结构立面图Fig.2 Elevation of structure

2 恢复力特性及振动微分方程

采用倒三角比例荷载，利用静力弹塑性分析源程序[10]对算例模型进行推覆分析，每一层得出如图3所示一条其斜率连续发生变化的光滑的恢复力-位移曲线。为了便于编制电算程序，往往在一定的原则下[11]以三根折线来替代连续发生变化的光滑的曲线，此三根折线定义为标准三线型骨架模型[12]。本文将各层的骨架曲线简化为标准的三线型恢复力模型，则其各层的恢复力特性参数如表2所示。其中，up1、up2分别表示第一、第二屈服位移，sk1、sk2、sk3分别表示第一、第二、第三屈服刚度。

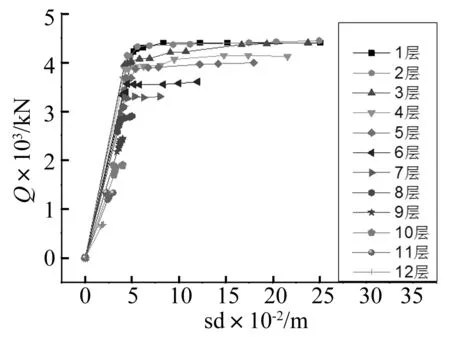
图3 各层恢复力-位移曲线 Fig.3 Restoring force-displacement curve of each story

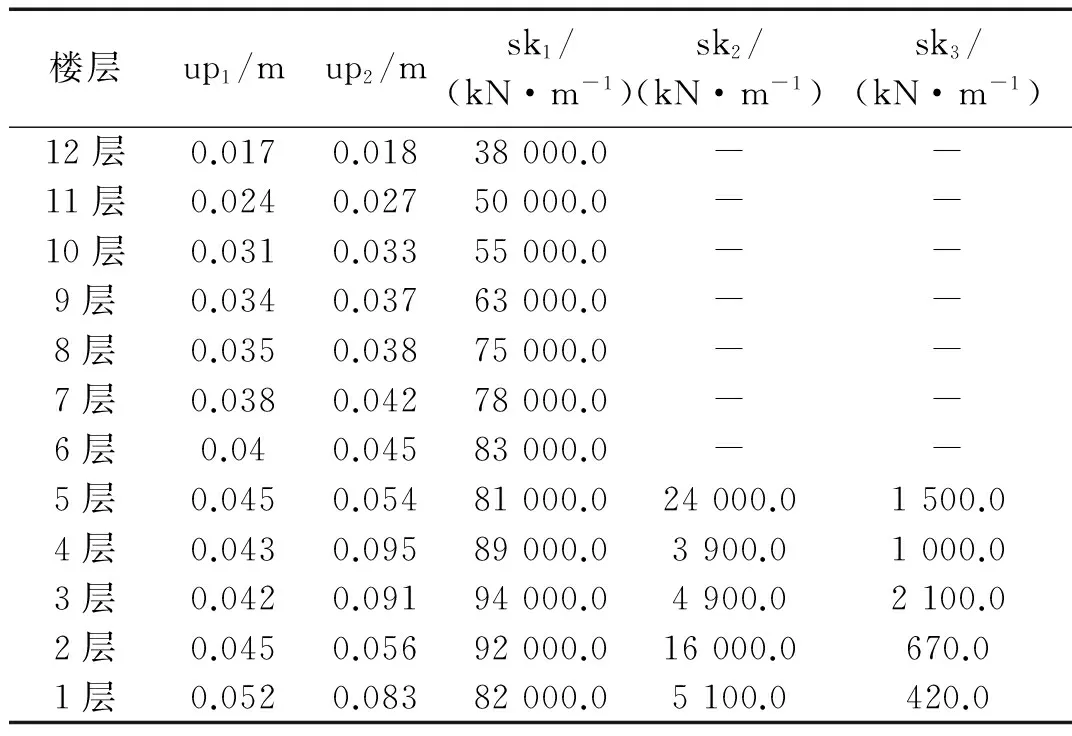
楼层up1/mup2/msk1/(kN·m-1)sk2/(kN·m-1)sk3/(kN·m-1)12层0.0170.01838000.0--11层0.0240.02750000.0--10层0.0310.03355000.0--9层0.0340.03763000.0--8层0.0350.03875000.0--7层0.0380.04278000.0--6层0.040.04583000.0--5层0.0450.05481000.024000.01500.04层0.0430.09589000.03900.01000.03层0.0420.09194000.04900.02100.02层0.0450.05692000.016000.0670.01层0.0520.08382000.05100.0420.0

将选取的一榀框架简化为多质点剪切型振动模型(见图2)，其振动微分方程[9]为

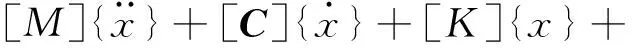
(1)

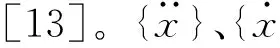
3 黏弹性阻尼器

本文所选取的阻尼器材料是日本住友3M开发的黏弹性材料(丙烯)，其材料特性为储存刚度较高、滞回曲线饱满，具有较大的变形能力(剪切变形能达到300%)，温度和加载周期变化对其吸收能量的性能影响较小。

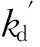
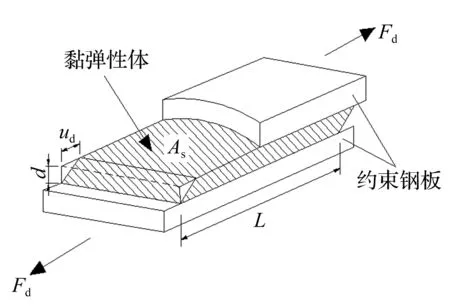
图4 黏弹性阻尼器结构示意图Fig.4 Schematic diagram of structures of viscoelastic damper

4 地震反应分析

采用Wilson-θ法[9]自编上述算例模型的弹塑性时程分析的电算程序，利用地震动作用下第m次循环后主结构的地震反应值，并根据分数微分模型[13]计算黏弹性阻尼器产生的阻尼力，将所得阻尼力代入到主结构第m+1次循环，从而求得结构第m+1次循环的阻尼力，如此循环往复直至所有时间点的地震动计算结束。

文稿采用两条记录波(Elcentro波、Kobe波)和两条人工波(Art Elcentro波、Art Kobe波)进行弹塑性时程分析。其中Art Elcentro波和Art Kobe波是以我国的设计用速度谱为目标谱，基于Elcentro 1940 NS记录波的相位特性和Jma Kobe 1995 NS记录波的相位特性而制成的，通过对地震波的频度-周期分析和加速度谱分析(阻尼比为0.05)可知，Art Elcentro波的卓越周期为0.1～0.4 s；Art Kobe波的卓越周期为0.16～0.5 s。

依据卓越周期的长短，将地震动可分为长周期地震动和短周期地震动。文稿的研究对象的固有自振周期为属于短、中周期，所以就偏重考虑了卓越周期为短周期的地震动。

图5表示地震波时程曲线，加速度峰值均调幅至4.0 m/s2，时间间隔为0.01 s，作用时间均取50 s。

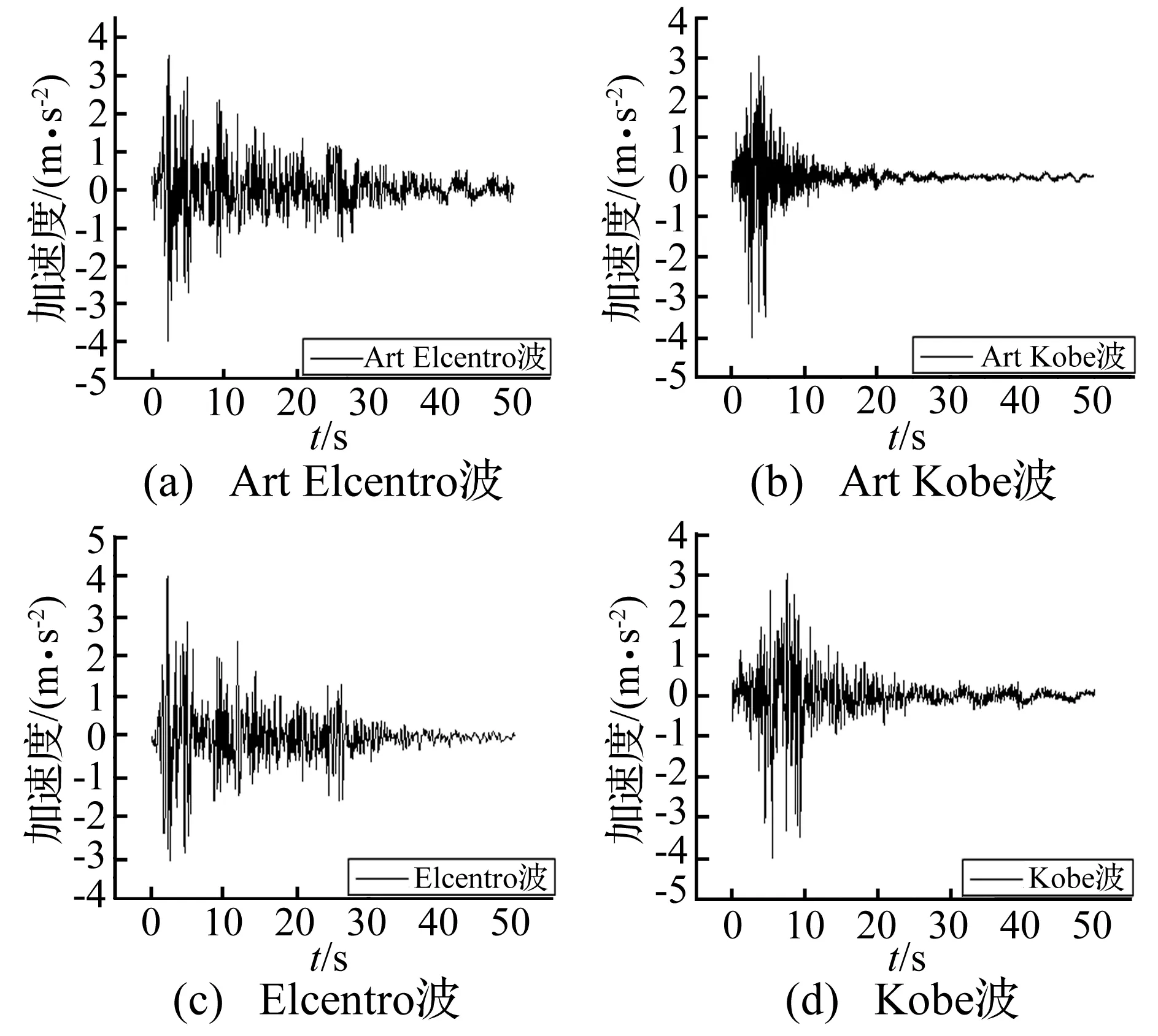
图5 地震波的选取Fig.5 Selection of seismic wave

4.1 地震动作用下的位移反应

利用四条地震动计算地震反应后，为了避免繁琐的叙述，在图6中仅表示Art Elcentro波第12层和Kobe波第1层“0倍”和“4倍”结构的位移反应时程曲线，图7表示各层的最大位移反应值。由图6可知，在地震动作用下，原结构在反应过程中会出现偏离其平衡位置的现象，而消能减震结构中阻尼器能够补强结构刚度，使结构发挥自复位功能，保证结构在反应过程中不发生偏离。由图7并计算结构各层的位移反应最大值降低率((0倍最大位移～4倍最大位移)/0倍最大位移)，可以看出，结构的位移最大值均减小，且降低率可达到25% 以上。

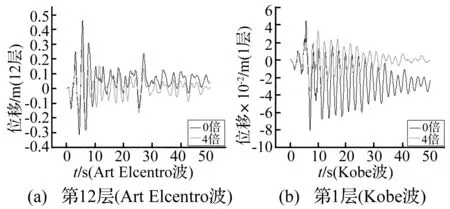
图6 结构第12层和第1层的位移反应Fig.6 Displacement response of the twelfth and first story of the structure

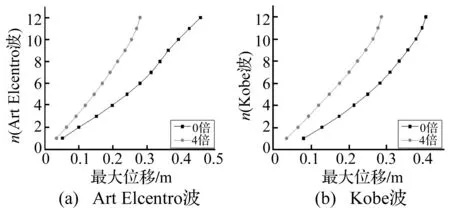
图7 结构各层的最大位移Fig.7 Maximum displacement of each story of the structure

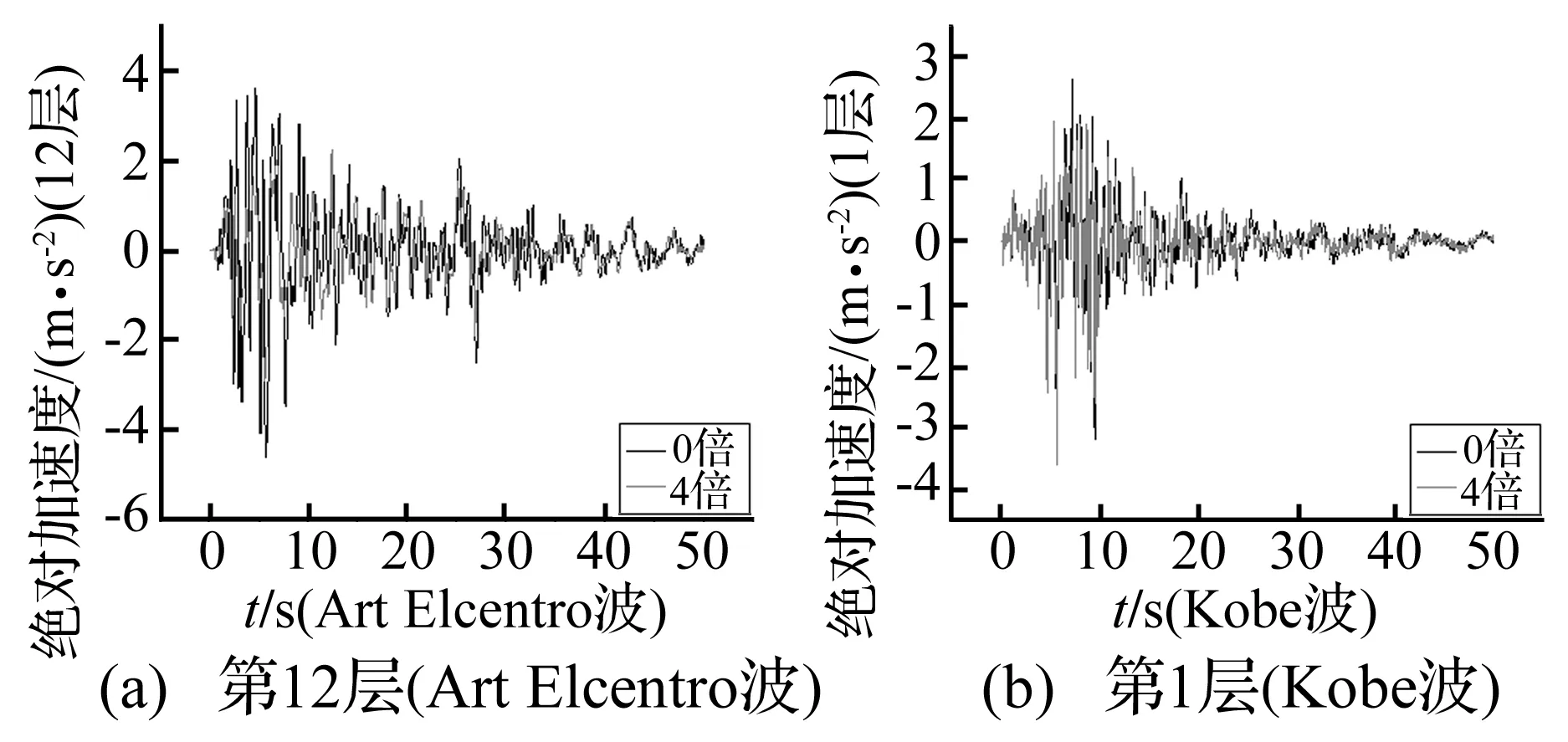
图8 结构第12层和第1层的绝对加速度Fig.8 Absolute acceleration response of the twelfth and first story of the structure

4.2 地震动作用下的绝对加速度反应

在图8中仅表示Art Elcentro波第12层和Kobe波第1层“0倍”和“4倍”结构的绝对加速度反应时程曲线，图9表示各层的最大绝对加速度反应值。

由图8、9并根据图9计算结构各层的绝对加速度反应最大值降低率((0倍最大绝对加速度～4倍最大绝对加速度)/0倍最大绝对加速度)。可以看出附加阻尼器后结构的绝对加速度反应明显减小，个别楼层降低率可达49.9%，充分表明黏弹性阻尼器具有较高的附加阻尼比的功能。

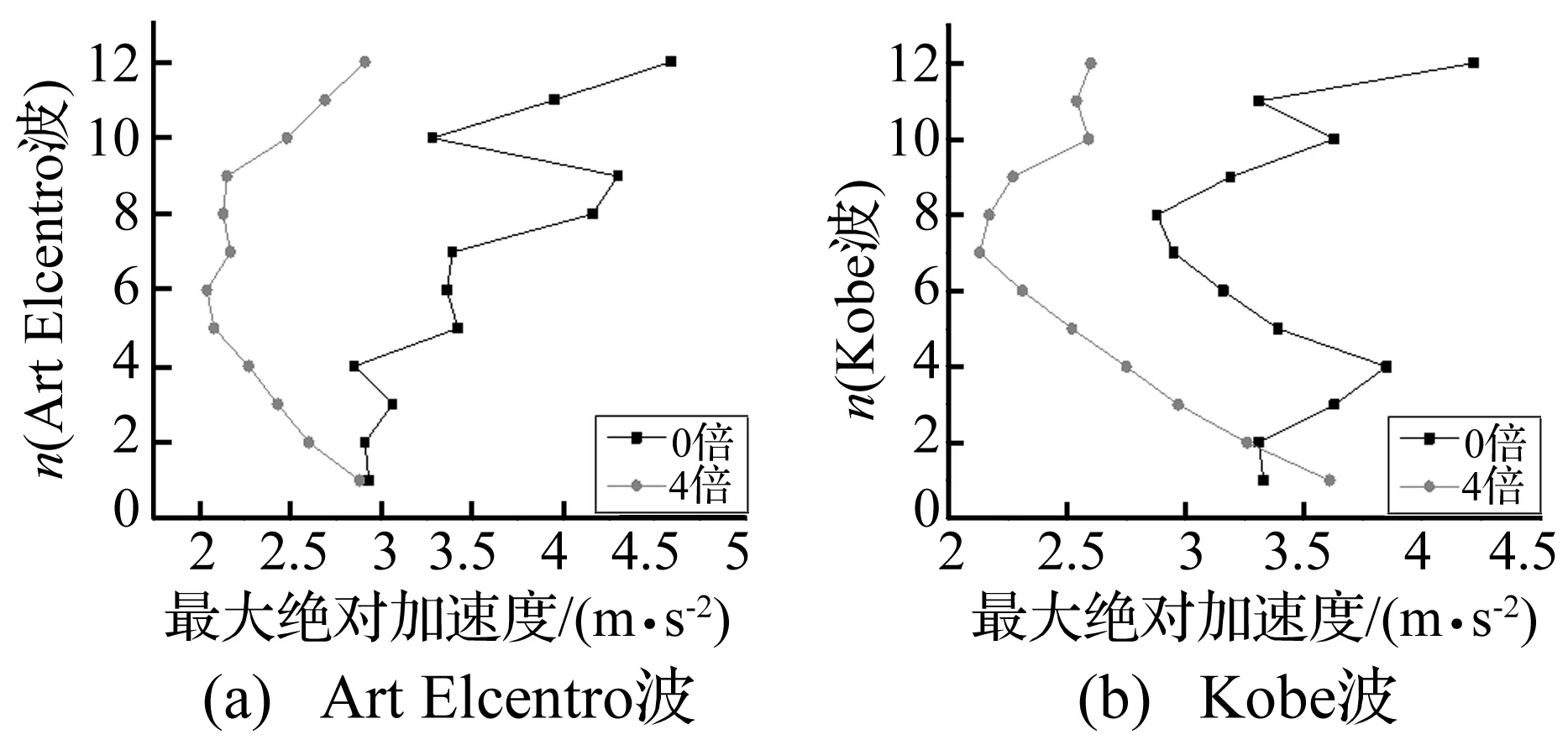
图9 结构各层的最大绝对加速度Fig.9 Maximum absolute acceleration of each story of the structure

4.3 允许层间位移角的验算

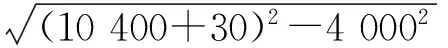
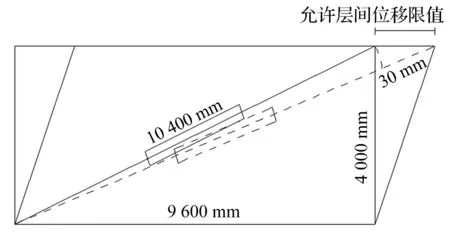
图10 层间位移角限值Fig.10 The limit of interstory drift ratio

图11表示“0倍”和“4倍”结构的层间位移角最大值、大小为1/50的《建筑抗震设计规范》所规定的罕遇地震作用下的层间位移角“规范限值”和上述的“阻尼器限值”，并由此计算结构各层层间位移角降低率((0倍层间位移角～4倍层间位移角)/0倍层间位移角)。可知，在四条地震动作用下，消能减震结构各层的层间位移角明显小于原结构的层间位移角，且都在规范规定和阻尼器允许的限值内，一些层最大降低率可达到73%。

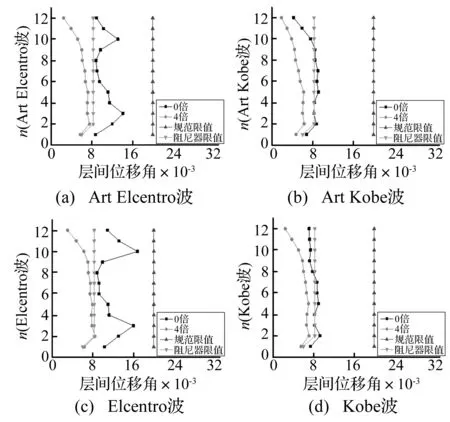
图11 结构各层的最大层间位移角Fig.11 Interstory drift ratio of each story of the structure

4.4 地震动作用下的剪力反应

在图12中，“0倍”表示不加阻尼器的原结构的框架承受的剪力；“4倍”表示附加阻尼器的消能减震结构的框架承受的剪力；“阻尼器”表示阻尼器承受的剪力；“4倍+阻尼器”表示附加阻尼器的消能减震结构承受的剪力。由图可知，由于阻尼器承受一部分剪力，所以消能减震结构各层的最大剪力明显减小，最大剪力降低率可达到20%～60%。

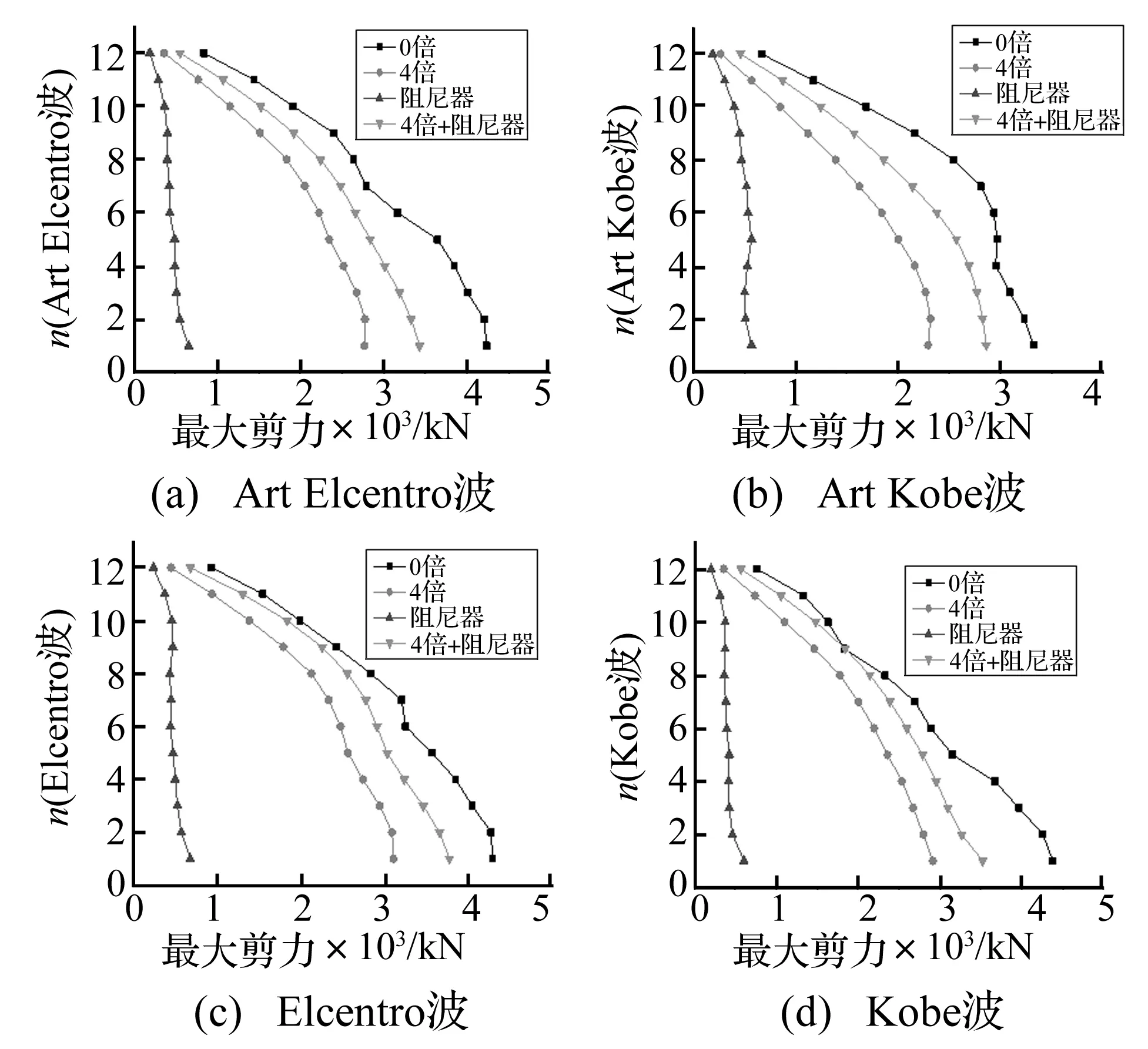
图12 结构及阻尼器各层剪力最大值分布Fig.12 The maximum shear force distribution of the structure and the dampers

5 能量分配

利用图13比较四条地震动作用下结构加(4倍)与不加(0倍)阻尼器时的地震动输入于结构的能量e的大小。由图可知，该能量的大小与不同的地震动和是否附加阻尼器均具有相关性。

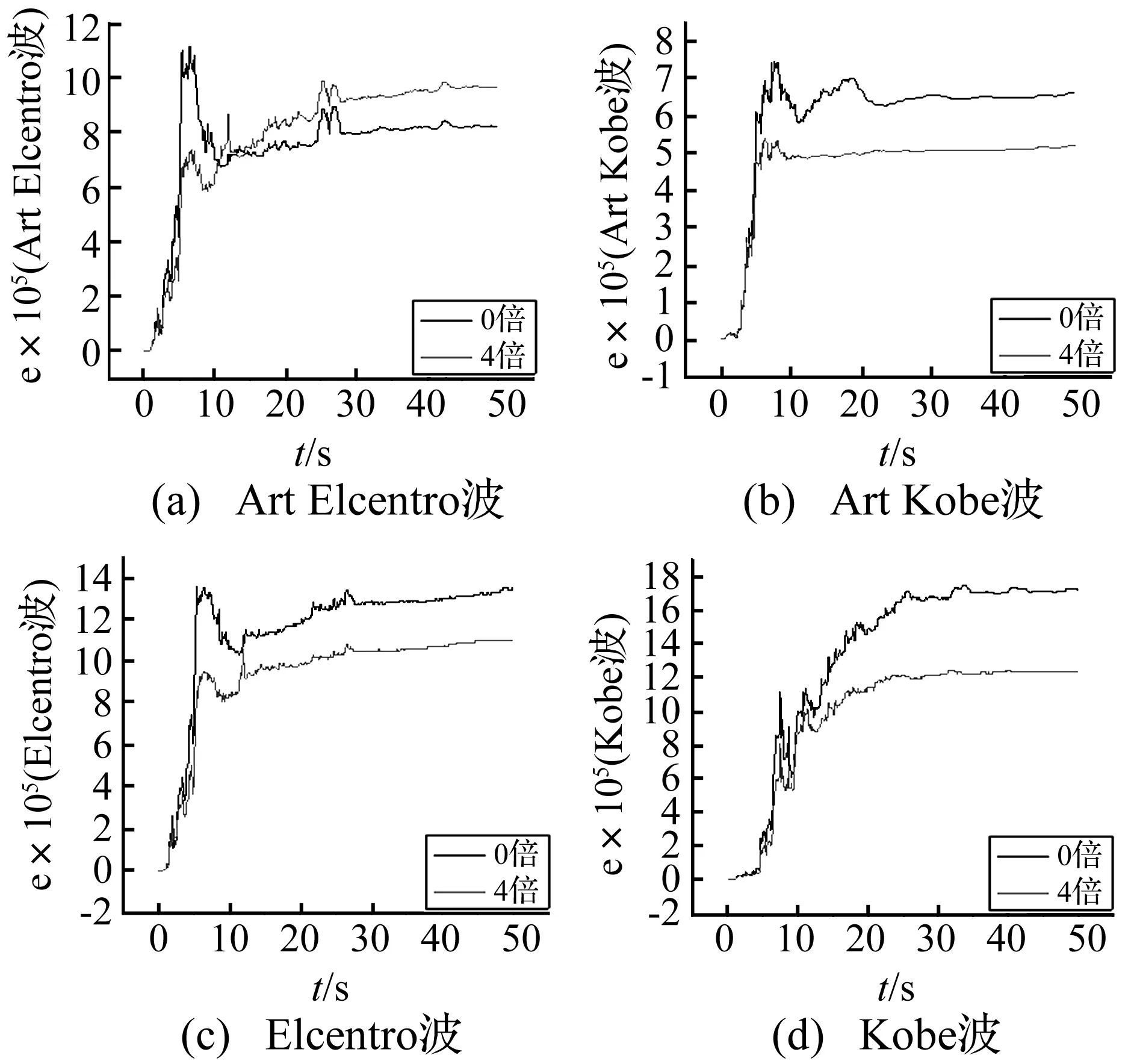
图13 地震输入能量比较Fig.13 Comparison of seismic input energy

图14表示在四条地震动作用下，附加4倍阻尼器的消能减震结构的能量分配分布。其中，e表示地震动输入于结构的能量；Wehp表示质点系动能+框架内部阻尼消耗的能量+框架弹塑性变形能量；Wd表示阻尼器消耗的能量；Wehpd表示Wehp和Wd的叠加，即消能减震结构消耗的总能量。从图中可以看出，地震动输入于结构的能量和构消耗的总能量几乎相等，即满足守恒，故可以讲程序的运行是可靠的。

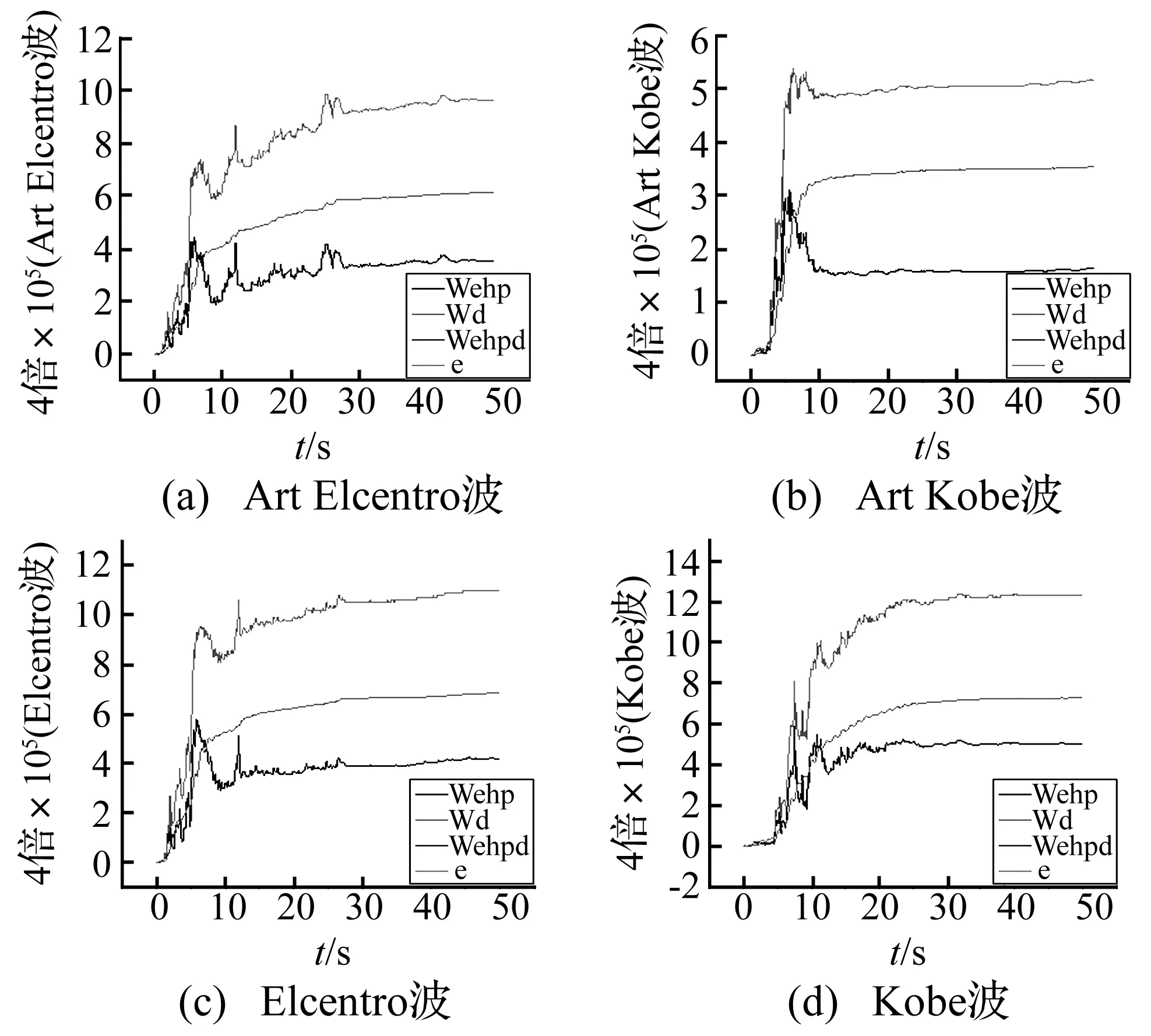
图14 消能减震结构的各部分耗能比较Fig.14 Comparison of energy dissipation of each part of the energy dissipation structure

图15表示在四条地震地震动作用下，“0倍”和“4倍”结构动能(或势能)We与输入能量e的比值，从图中可以看出，附加阻尼器以后动能(或势能)减少，这就以能量角度说明附件阻尼器后减少势能，即减少水平位移。

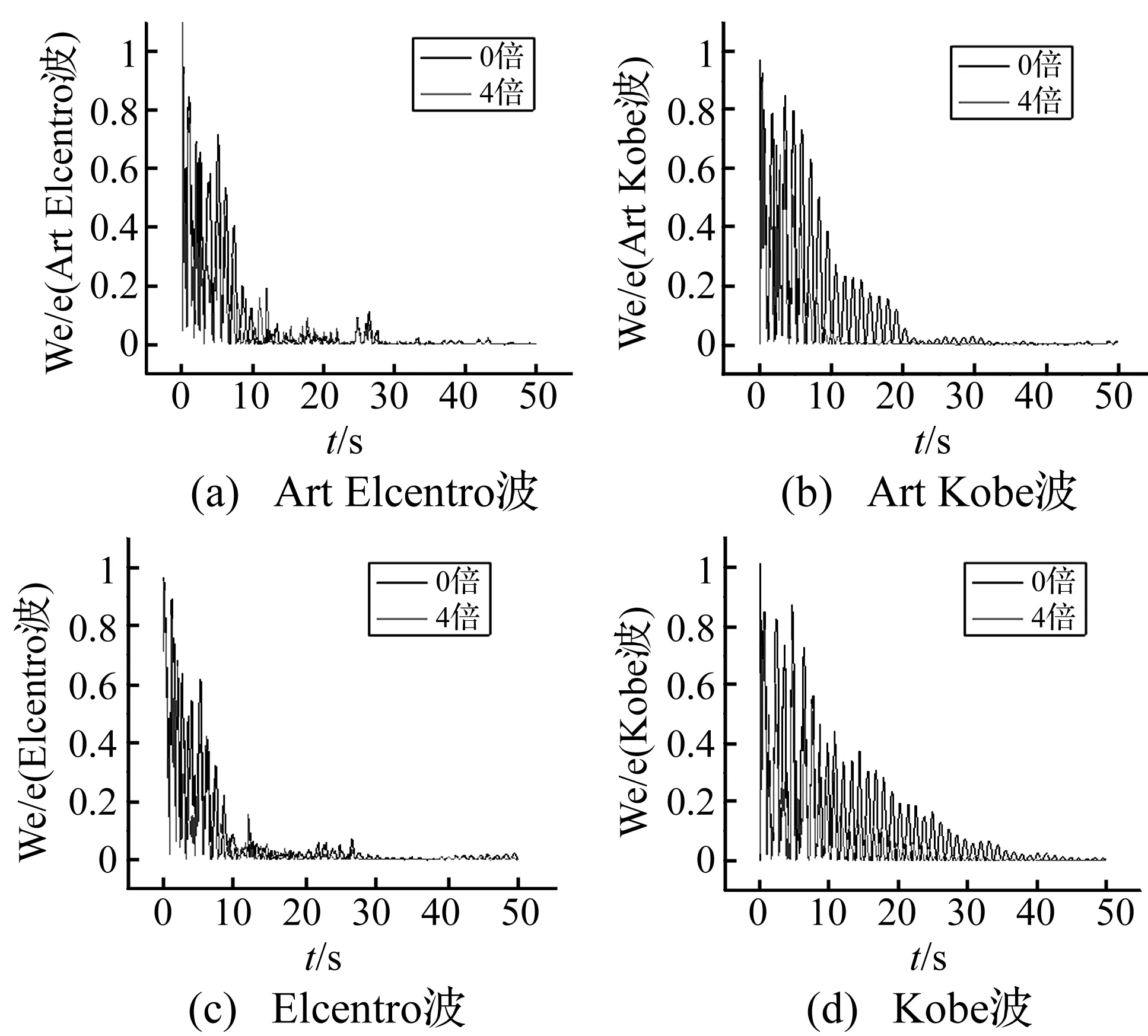
图15 动能We占地震输入能量e 的比例Fig.15 Kinetic energy We accounts for the seismic input energy e

图16表示在4条地震地震动作用下，“0倍”和“4倍”结构框架内部阻尼消耗的能量Wh与输入能量e的比值。从图中可以看出，附加阻尼器以后框架内部阻尼消耗的的能量几乎减少到一半，可以遏制结构构件不必要的温度的上升。

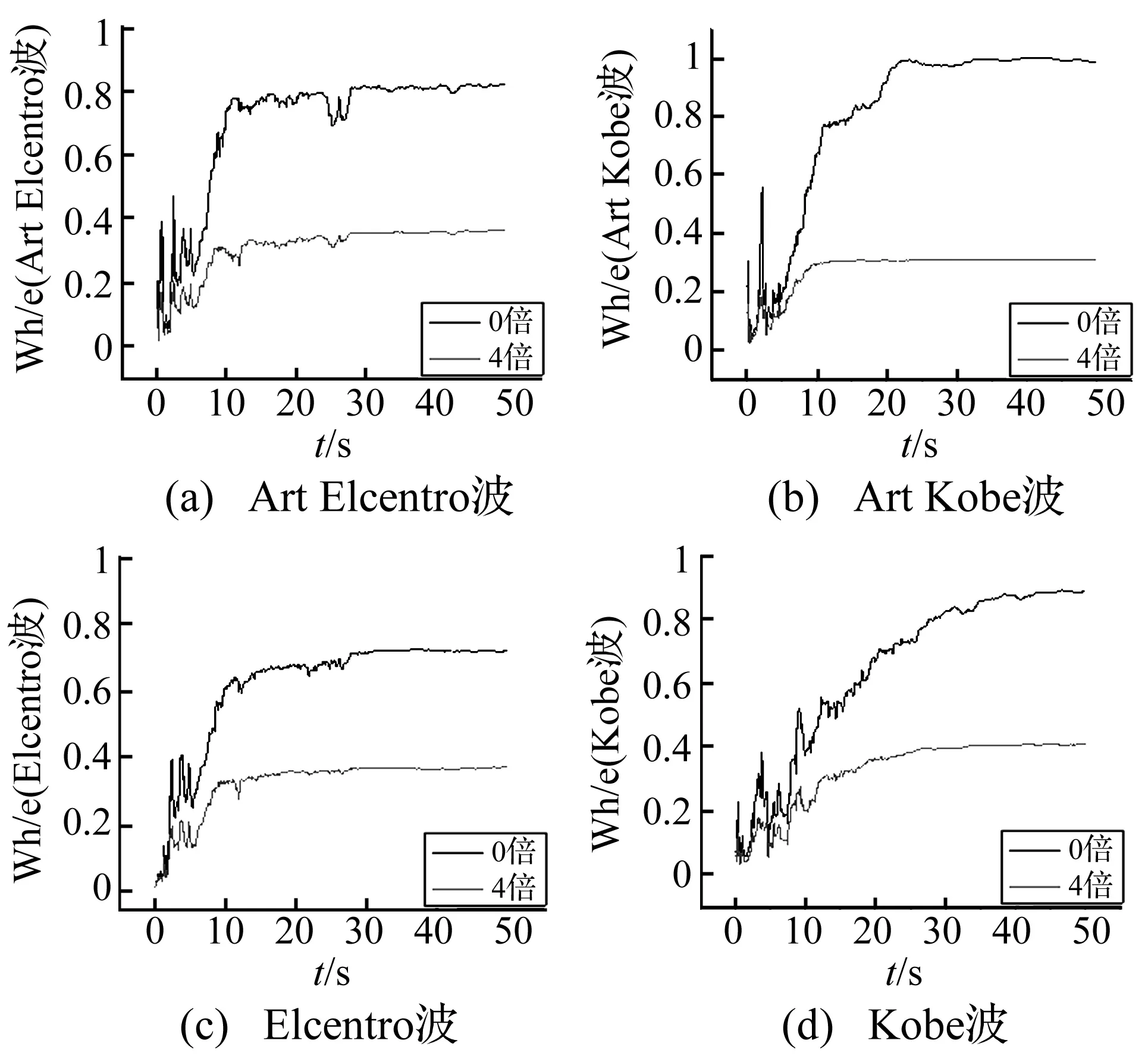
图16 内部阻尼消耗能Wh占地震输入能量e 的比例Fig.16 Internal damping energy Wh accounts for the seismic input energy e

图17表示在4条地震地震动作用下，“0倍”和“4倍”结构框架消耗的弹塑性变形能Wp与输入能量e的比值。从图上可以看出，附加阻尼器后减少弹塑性变形能，在一定程度上遏制主体结构的损伤(弹塑性变形)，保证“中震不坏、大震可修”的现代设计理念。

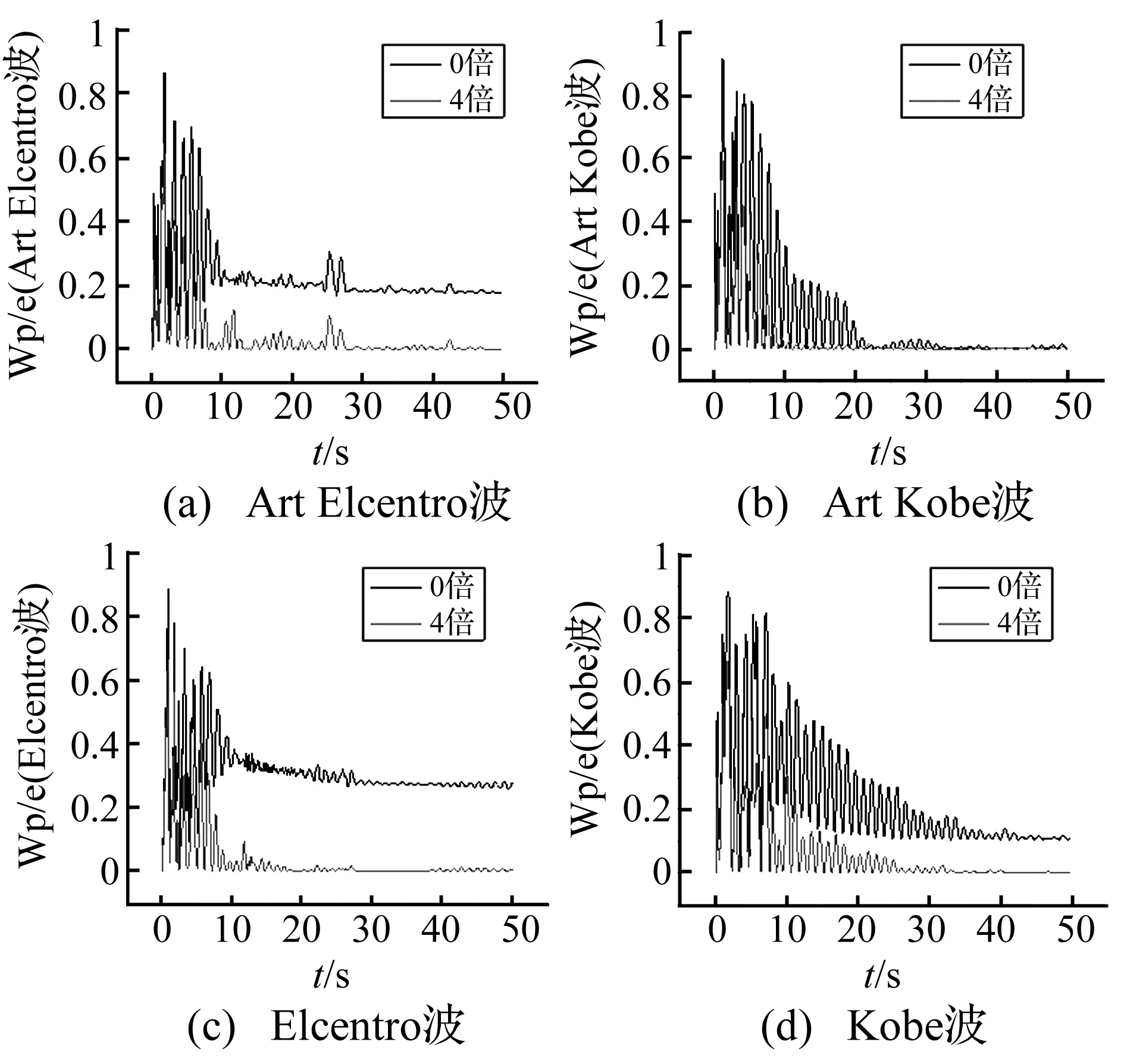
图17 结构变形能Wp占地震输入能量e 的比例Fig.17 Structural deformation energy Wp accounts for the seismic input energy e

在图18中，“0倍”表示原结构的总耗能占地震动输入于结构的能量比例，“4倍”表示消能减震结构中主体结构本身的耗能占地震动输入的能量比例，“Wd/e”表示消能减震结构中的阻尼器耗能占地震输入能量的比例。由图可知，不加阻尼器的结构其地震动输入于结构的能量全部由主体结构本身所消耗，而消能减震结构的主体结构本身消耗的能量仅占地震动输入的能量的30%～40%，阻尼器耗能可达60%～70%。

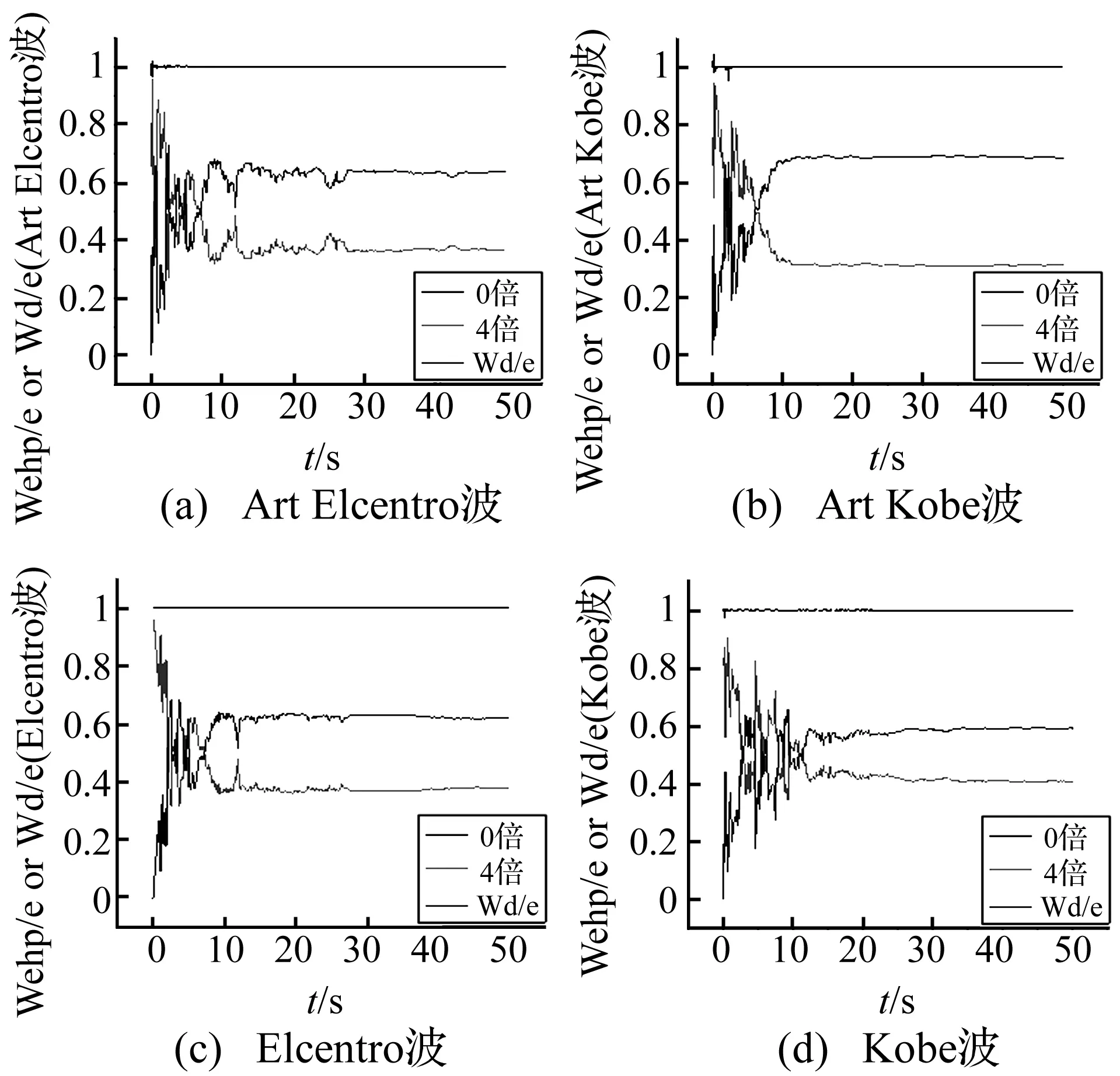
图18 结构总耗能Wehp占地震输入能量e 的比例Fig.18 Structure total energy consumption accounts for the seismic input energy e

图19为以百分比堆积条形图形式表达的能量的分配。其中1、3、5、7表示“0倍”结构的能量分配；2、4、6、8表示“4倍”结构的能量分配。由图可知，原结构的We所占比例很小，地震输入能量主要由Wh和Wp消耗，消能减震结构60%的地震输入能量被阻尼器消耗，结构本身阻尼耗能和变形耗能大大减少。

可见，附加阻尼器后能量的分配发生变化，向有利于消能减震方向发展。

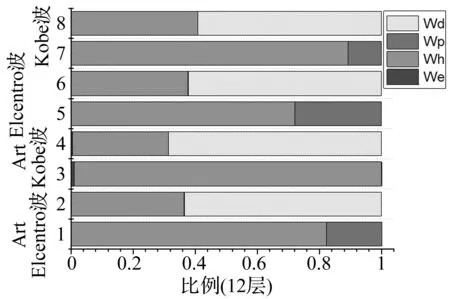
图19 12层结构各种能量比例Fig.19 Various energy ratio of the 12 story structure

5.1 阻尼器滞回曲线

黏弹性阻尼器在发挥耗能作用时会出现软化和硬化的现象，现选取Elcentro波作用下结构第12层阻尼器的滞回曲线对这两种特性进行研究，如图20。为使效果更直观清晰，对滞回曲线进行分解，图20(a)为前1 000个时间点的滞回曲线，图20(b)为前5 000个时间点的滞回曲线。图20(a)中1～5分别表示滞回曲线的第1～5圈，可以看出，标注1的储存刚度(滞回环的斜率)最大，可认为阻尼器初期发生了硬化现象；且滞回曲线大致呈现出随标注增大储存刚度逐渐减小的趋势，即阻尼器发生了软化现象。

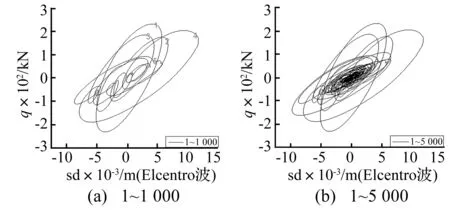
图20 黏弹性阻尼器的滞回曲线Fig.20 The hysteretic curve of viscoelastic dampers

5.2 结构滞回曲线

图21对原结构与消能减震结构的恢复力-位移曲线进行了比较，仅列出Art Elcentro波第12层和Kobe波第1层，可以得出，原结构在地震动作用下会进入塑性阶段，而消能减震结构能保证结构在受到地震动作用时始终保持在弹性阶段，避免了结构因发生塑性变形而产生的破坏。

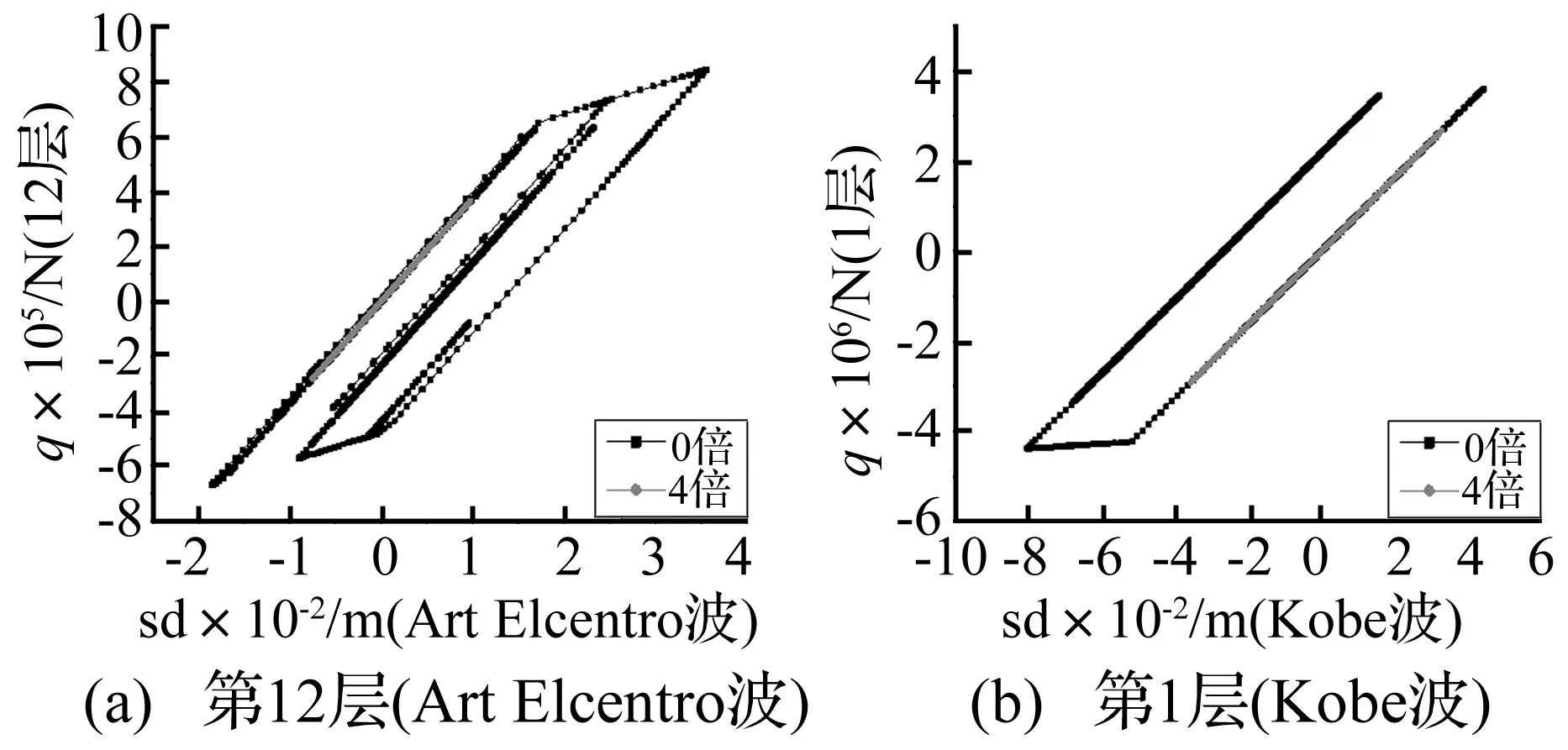
图21 结构各层的恢复力-位移曲线Fig.21 Restoring force-displacement curve of each story of the structure

6 阻尼器不同布设方式比较

分别讨论四条地震动作用下，原结构基础上五种工况的最大层间位移、最大位移、最大绝对加速度的比较。工况0表示不加黏弹性阻尼器，工况1表示黏弹性阻尼器设置在1～12层，工况2表示黏弹性阻尼器设置在1～6层，工况3表示黏弹性阻尼器设置在7～12层，工况4表示黏弹性阻尼器设置在偶数层。其中，工况1～4均采用“4倍”方式布置在相应楼层上。

6.1 不同工况的最大位移比较

图22表示四条地震动作用下，不同工况的最大位移比较。由图可知，工况1、2、3、4的最大位移小于工况0时的最大位移，即附件黏弹性阻尼器可以减小结构的最大位移反应。工况1优于工况3且优于工况4，工况2优于工况3且优于工况4，工况4优于工况3。

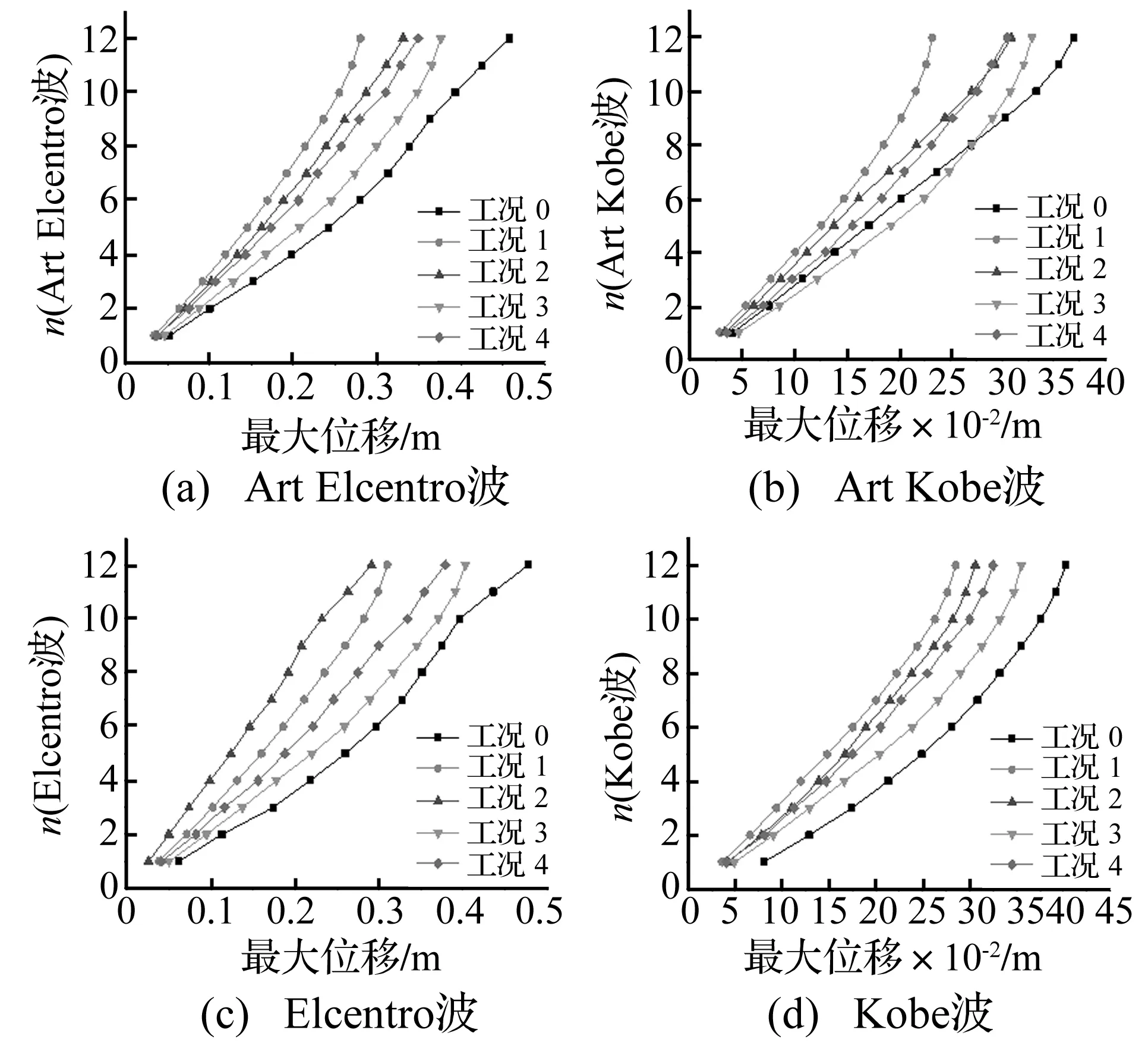
图22 不同工况的最大位移比较Fig.22 Comparison of maximum displacement under different operating conditions

6.2 不同工况的最大绝对加速度比较

图23表示四条地震动作用下，不同工况的最大绝对加速度比较。由图可知，工况1、2、3、4的最大绝对加速度小于工况0时的最大绝对加速度(在低楼层处有例外)，即附件黏弹性阻尼器可以减小结构的最大绝对加速度反应。

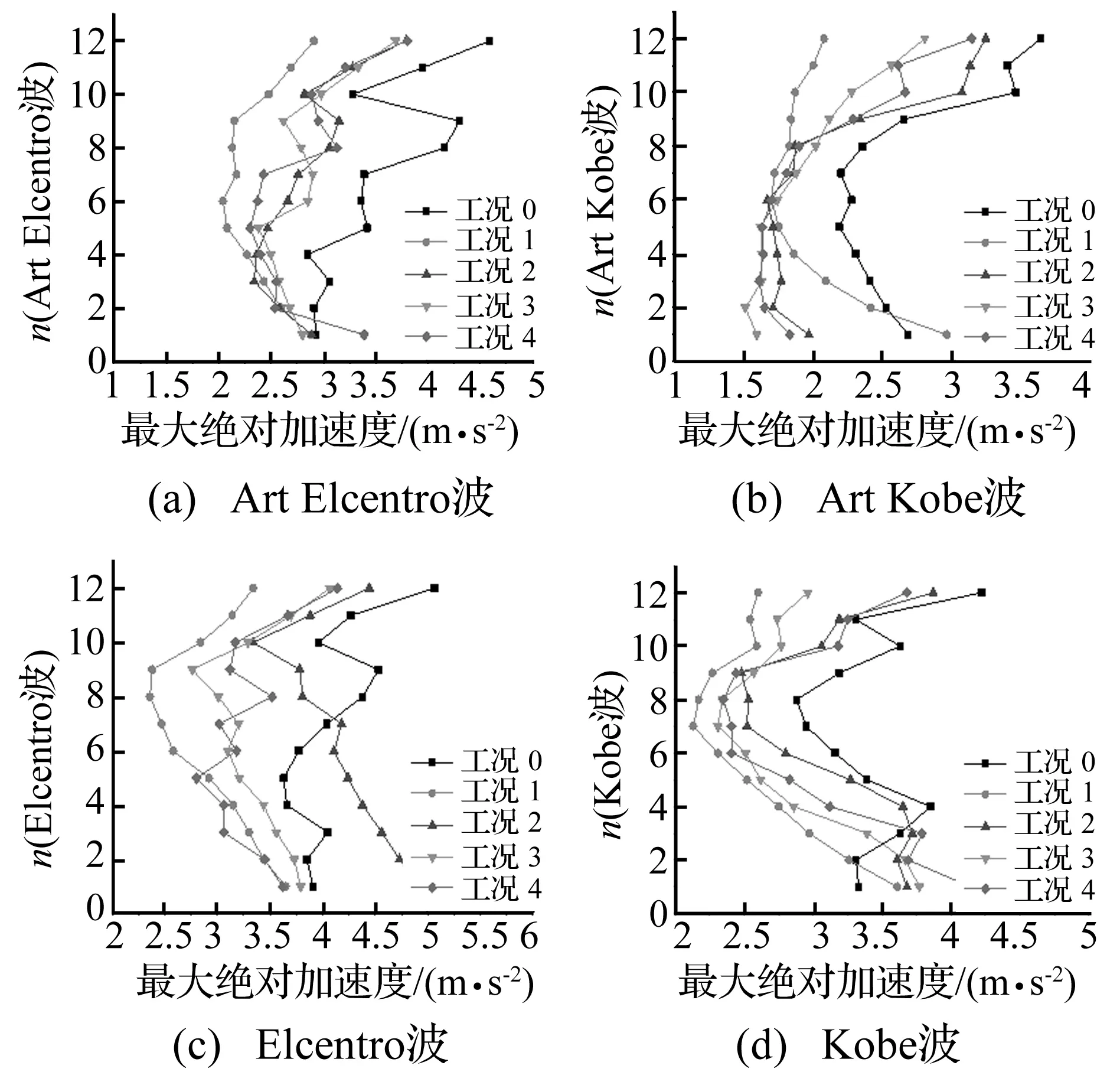
图23 不同工况的最大绝对加速度比较Fig.23 Comparison of maximum absolute acceleration under different operating conditions

6.3 不同工况的最大层间位移比较

图24表示四条地震动作用下，不同工况的最大层间位移比较。由图可知，总体来说，工况1、2、3、4的最大层间位移小于工况0时的最大层间位移，即附件黏弹性阻尼器可以减小结构的最大层间位移反应。工况1优于工况3且优于工况4，其余情况结果对比不明显。

综合比较几种工况的最大位移、最大绝对加速度以及最大层间位移，可以认为工况1，即在每一层都设置黏弹性阻尼器的结构减震效果是最好的。

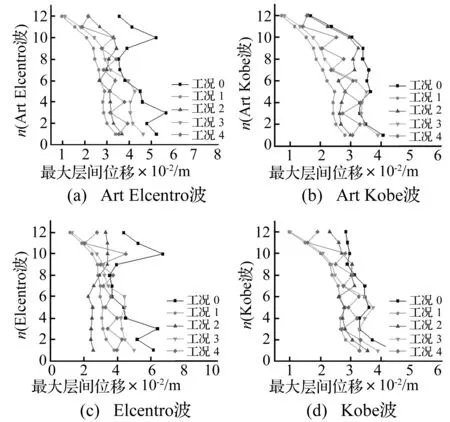
图24 不同工况的最大层间位移比较Fig.24 Comparison of maximum interstory displacement under different operating conditions

7 不同黏弹性阻尼器投放量的影响

7.1 不同阻尼器投放量的结构最大位移比较

仍采用上述四条地震动，对结构设置不同的黏弹性阻尼器投放量的最大位移、最大绝对加速度、最大层间位移进行计算比较。

图25表示不同地震动作用下，结构采用不同黏弹性阻尼器投放量时，结构各层的最大位移反应比较。由图可知，结构附加黏弹性阻尼器后，无论投放量采用多少倍，结构各层的最大位移反应均减小，这也验证了黏弹性阻尼器具有减震效果。除此之外，仍可得出，结构各层的最大位移反应并非随黏投放量的逐渐增加而逐渐减小，说明黏弹性阻尼器的减震效果并不是采用的黏弹性材料层越多其减震效果越好，而是存在一个转折点，以16倍为限值，当投放量小于等于16倍时，阻尼器的减震效果随投放量的增加而增大，而当投放量大于16倍时，其减震效果反而随投放量的继续增加而减小。

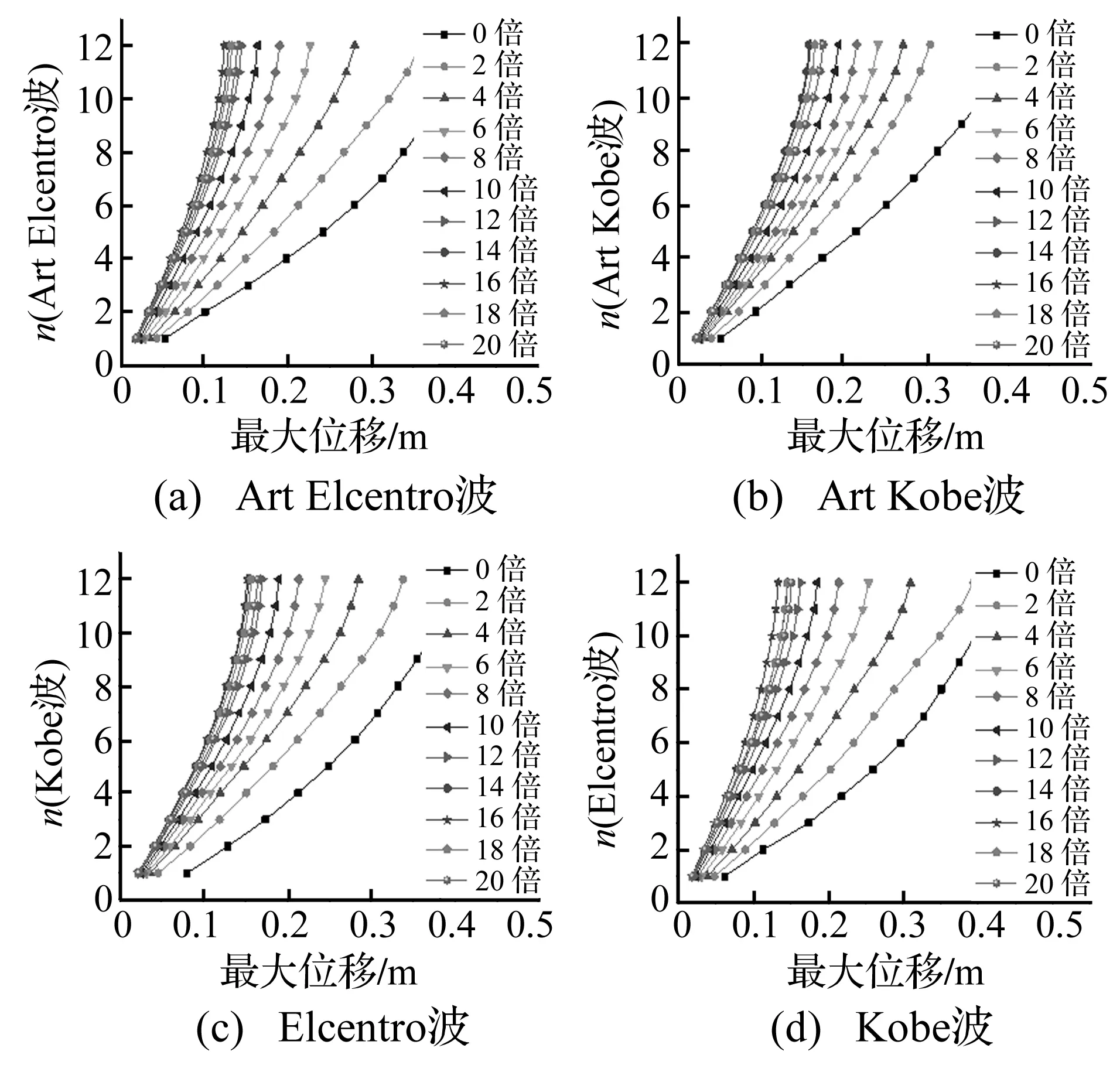
图25 不同阻尼器投放量结构最大位移比较Fig.25 Maximum displacement of each story of the structure with different delivery

7.2 不同阻尼器投放量的结构最大绝对加速度比较

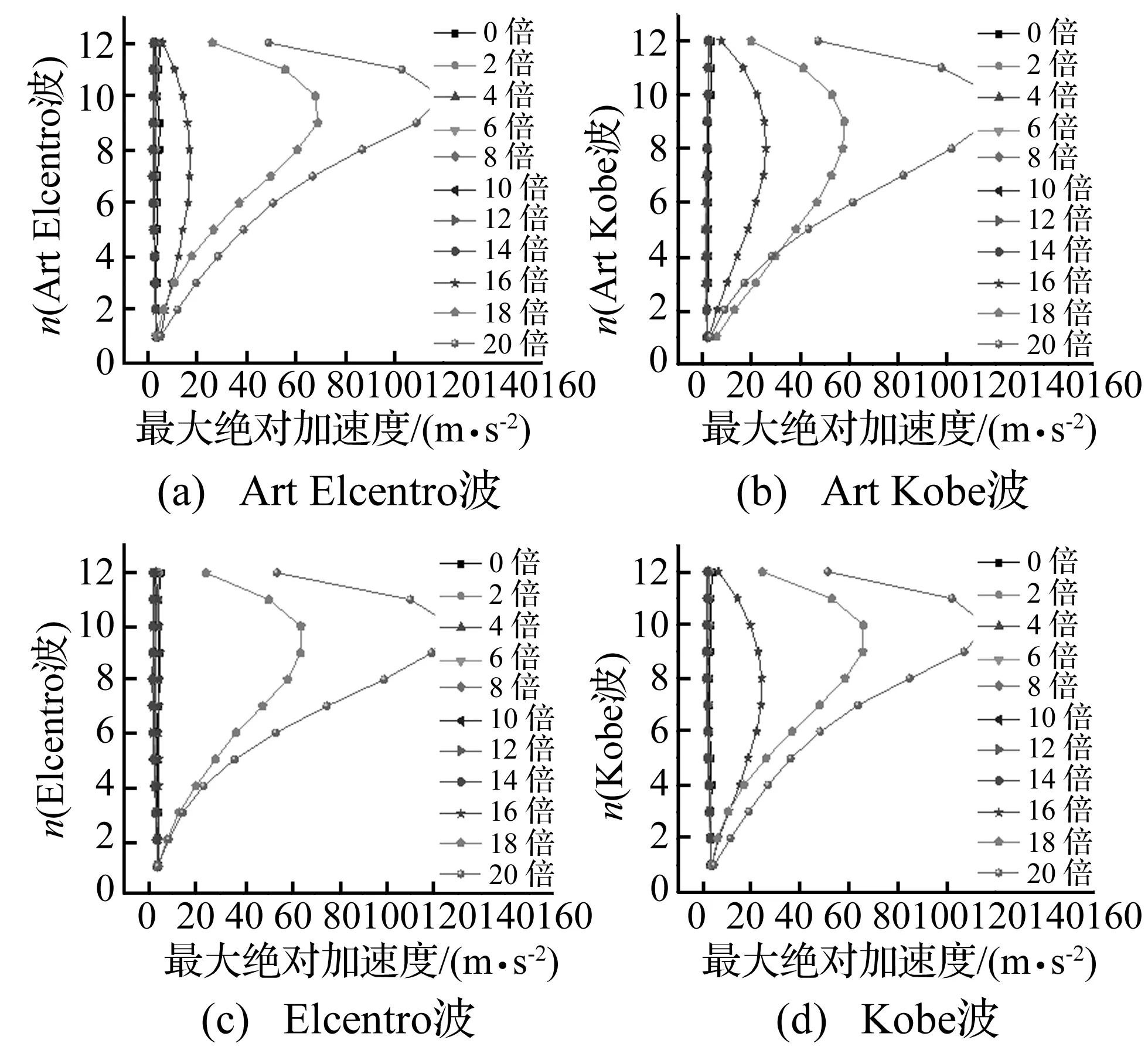
图26 不同阻尼器投放量结构最大绝对加速度比较Fig.26 Maximum absolute acceleration of each story of the structure with different delivery

图26表示不同地震动作用下，结构采用不同黏弹性阻尼器投放量时，结构各层的最大绝对加速度比较。由图可知，当投放量小于16倍时，结构的绝对加速度反应小于不加阻尼器时的最大绝对加速度反应；当投放量大于等于16倍时，结构的绝对加速度反应反而大于不加阻尼器时的最大绝对加速度反应。即结构各层的最大绝对加速度反应并非随投放量的逐渐增加而逐渐减小，说明黏弹性阻尼器的减震效果并不是采用的投放量越多其减震效果越好，而是存在一个转折点，以16倍为限值，当投放量小于16倍时，阻尼器的减震效果随投放量的增加而增大，而当投放量大于等于16倍时，其减震效果反而随投放量的继续增加而减小。

7.3 不同阻尼器投放量的结构最大层间位移比较

图27表示不同地震动作用下，结构采用不同黏弹性阻尼器投放量时，结构各层的最大层间位移反应比较。由图可知，结构附加黏弹性阻尼器后，无论投放量采用多少倍，结构各层的最大层间位移反应均减小(Elcentro波作用下，2倍黏弹性材料时，结构第8层除外)，且附加阻尼器后，结构的层间位移变化较均匀。除此之外，仍可得出，结构各层的最大层间位移反应并非随投放量的逐渐增加而逐渐减小，说明黏弹性阻尼器的减震效果并不是采用的投放量越多其减震效果越好，当投放量等于16倍时，阻尼器的减震效果随投放量的增加而增大，而当投放量大于16倍时，其减震效果反而随投放量的继续增加而减小。

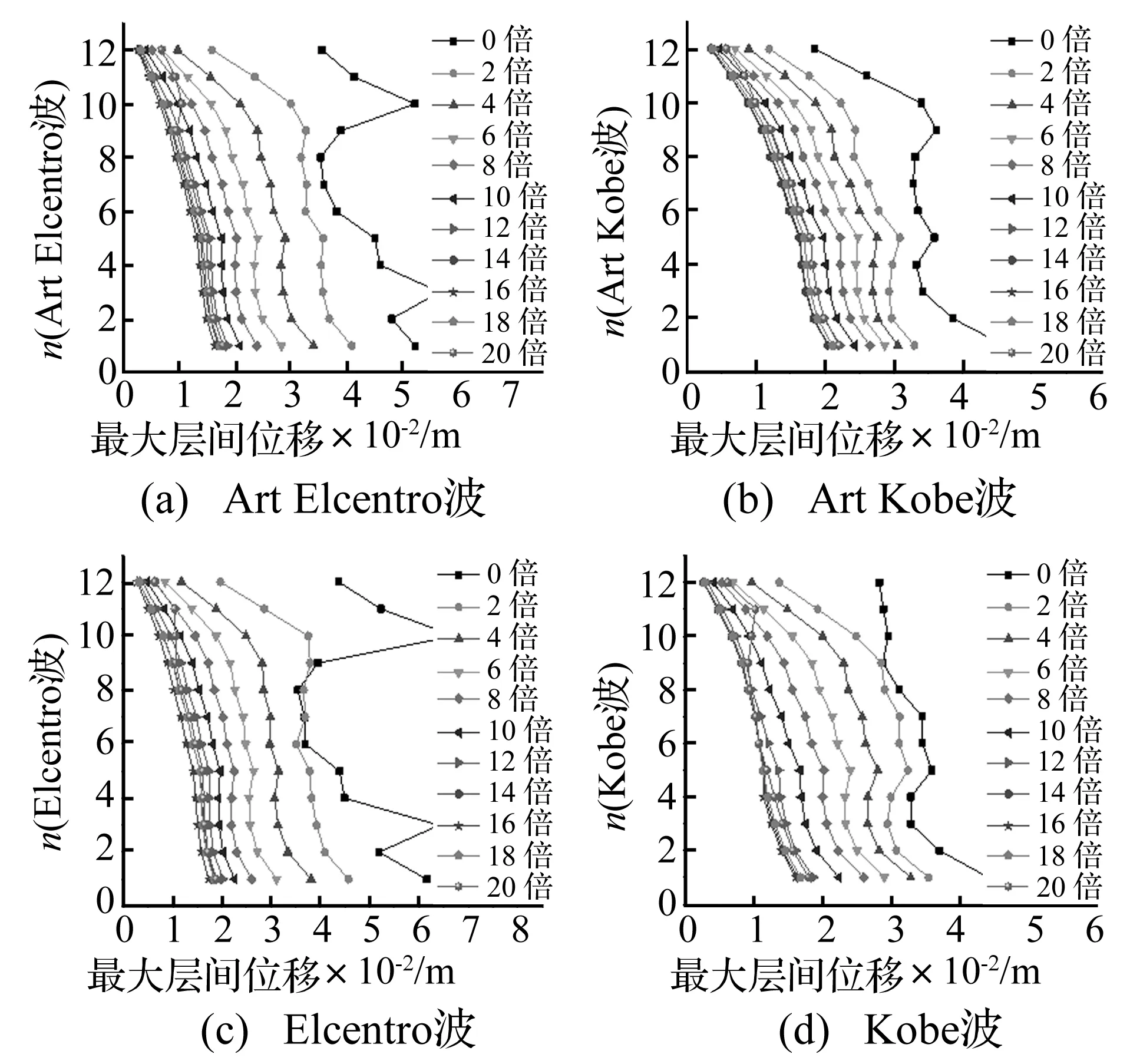
图27 不同阻尼器投放量结构最大层间位移比较Fig.27 Maximum interstory drift ratio of each story of the structure with differentdelivery

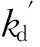
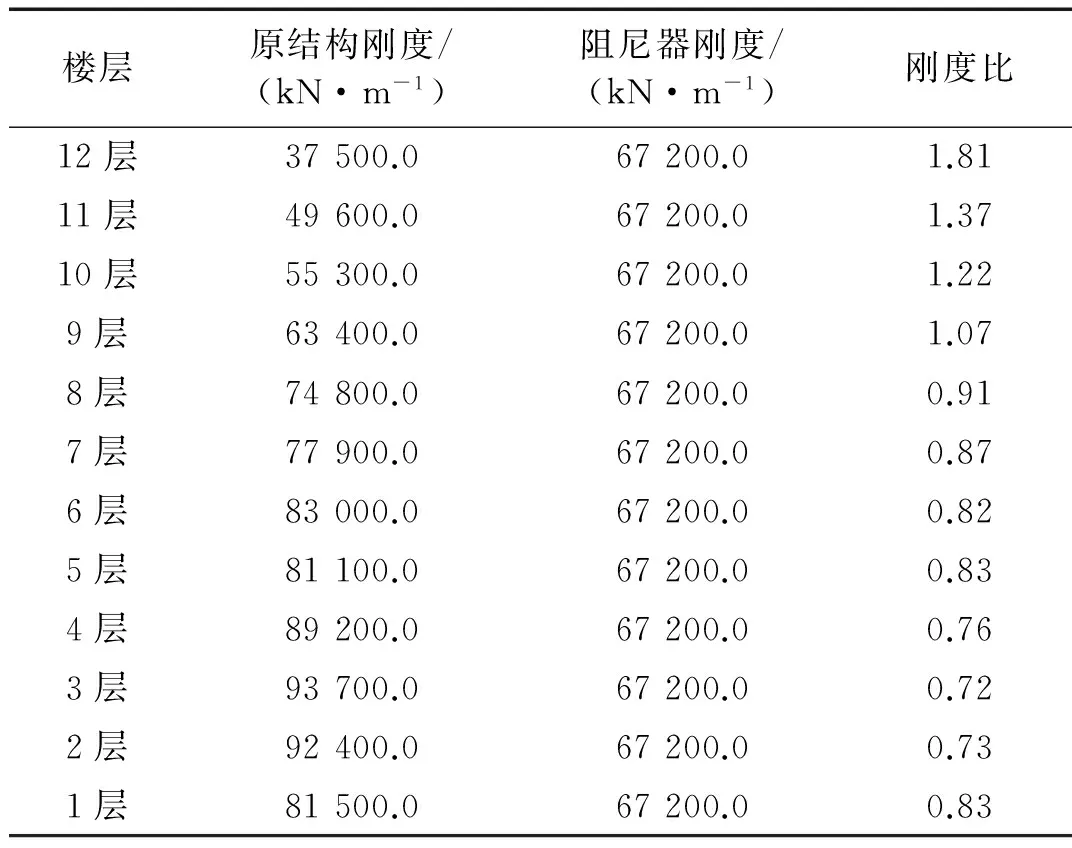
楼层原结构刚度/(kN·m-1)阻尼器刚度/(kN·m-1)刚度比12层37500.067200.01.8111层49600.067200.01.3710层55300.067200.01.229层63400.067200.01.078层74800.067200.00.917层77900.067200.00.876层83000.067200.00.825层81100.067200.00.834层89200.067200.00.763层93700.067200.00.722层92400.067200.00.731层81500.067200.00.83

将表3中阻尼器与原结构的刚度比与楼层关系采用最小二乘法进行曲线拟合，得出结构的刚度比与楼层关系的拟合公式：

λi=0.015i2-0.115i+0.95

(2)

式中：i表示层号，λi表示阻尼器与原结构的刚度比。

图28表示阻尼器与原结构刚度比与层数的关系曲线和式(2)表示的拟合曲线，从图中可以看出，式(2)能够较准确的反映结构刚度比和层数之间的关系。

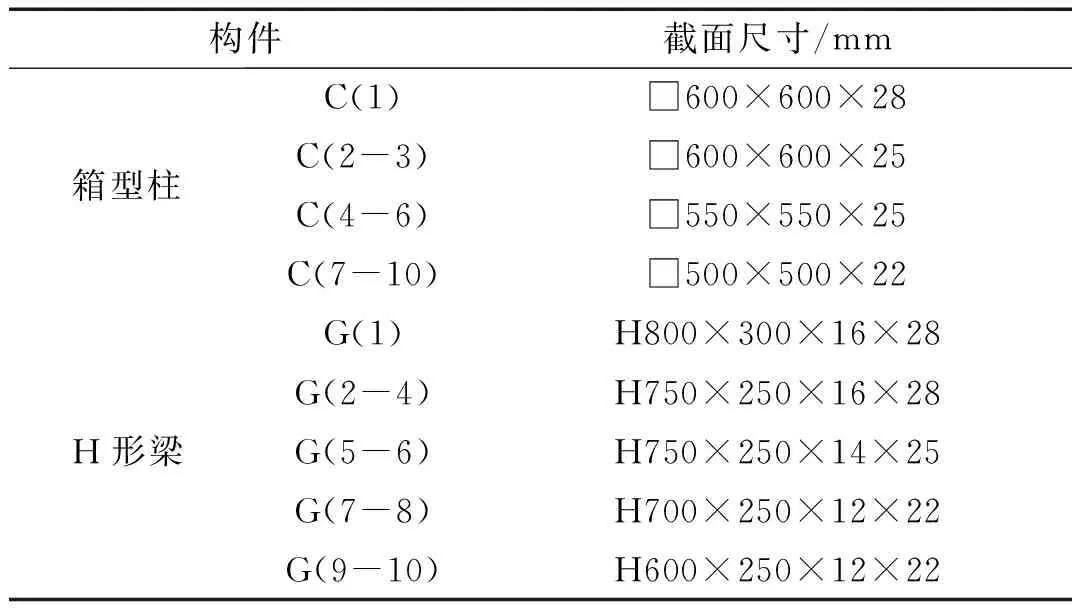
表4 梁、柱截面形式和尺寸

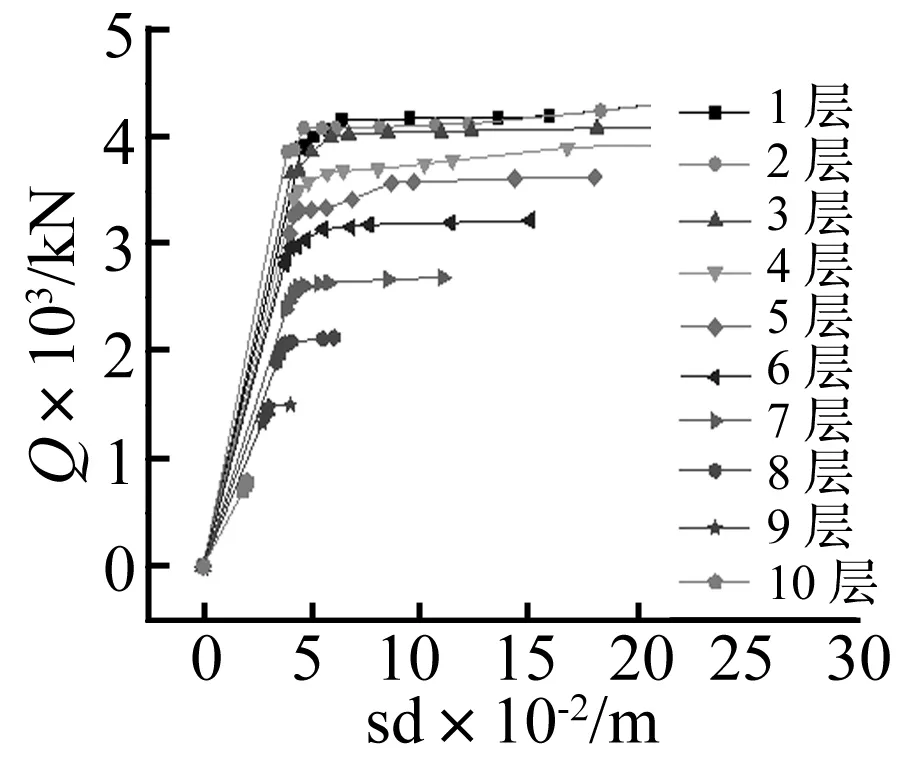
图29 10层结构各层恢复力-位移曲线Fig.29 Restoring force-displacement curve of each story of the 10 story structure

7.4 验证

采用一10层3跨钢框架算例模型对式(2)的结果进行验证，其梁、柱截面形式了尺寸见表4，所得其各层恢复力-位移曲线如图29，各层的恢复力特性参数如表5。

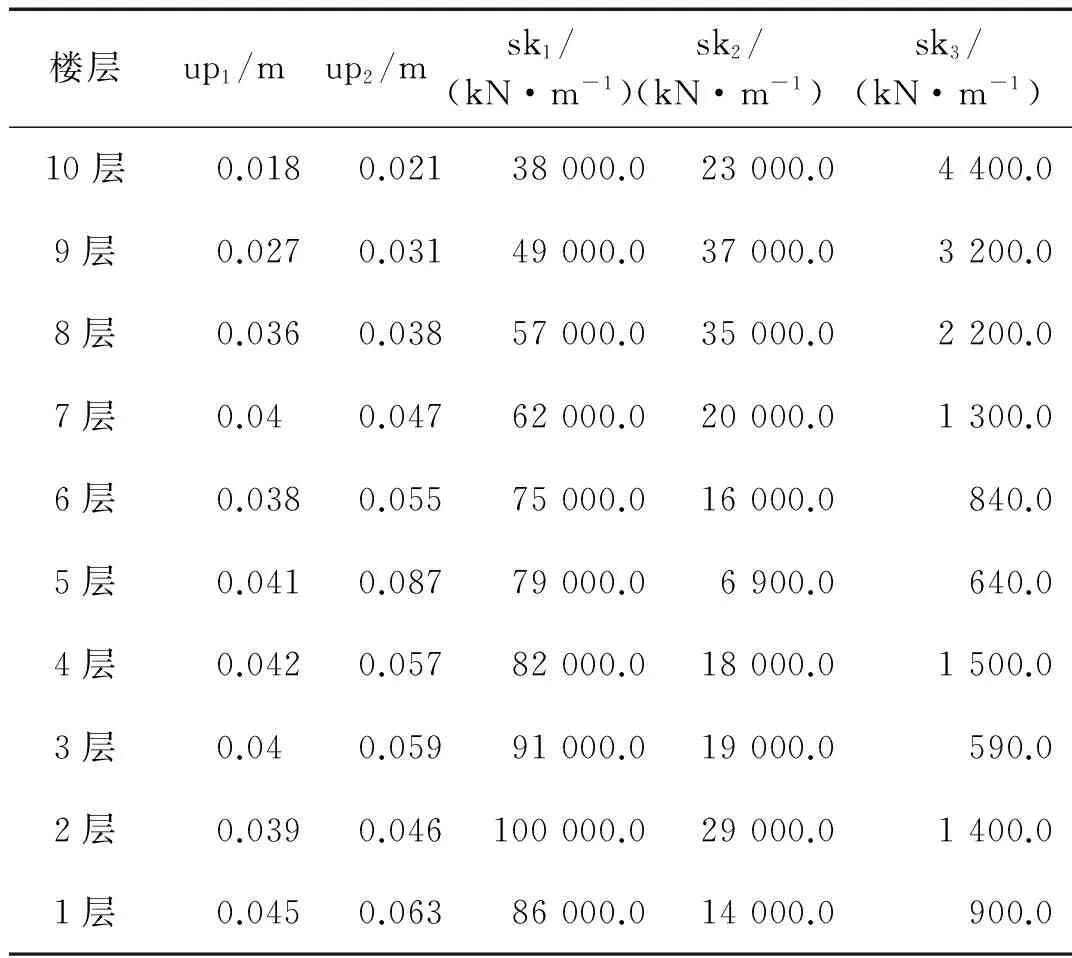
表5 10层结构各层恢复力特性参数

按式(2)得到10层结构各层应设置的阻尼器与结构的刚度比如表6，由刚度比计算阻尼器的储存刚度，并根据上述阻尼器的储存刚度与储存剪切弹性模量的关系，计算各层应附加的阻尼器的剪切面积As(假设阻尼器厚度为10 mm)，即采用表6中的剪切面积对结构各层的黏弹性阻尼器进行设置，可以使减震效果达到较优的状态。

按照式(2)计算的阻尼器投放量对一10层钢框架结构模型进行弹塑性时程分析，用以验证式(2)的正确性和通用性，图30(a)～(c)分别表示结构各层的最大位移、最大绝对加速度以及最大层间位移，“0”表示原结构，“4 m2”、“5 m2”、“6 m2”(式(2)计算的剪切面积每一层都不同，在进行时程分析时存在一定的难度，此处为近似取值)表示不同剪切面积的阻尼器的消能减震结构。由图可知，按式(2)确定的阻尼器投放量能够在很大程度上减小结构的最大位移、最大绝对加速度以及最大层间位移反应。在图中选用的三种剪切面积的阻尼器中，最大位移和最大层间位移随剪切面积的增大减震效果增加，而最大绝对加速度并不随投放量的增加而逐渐增加，“6 m2”反而出现增大的现象(图中仅列出Art Elcentro的情况，采用Art Kobe波、Elcentro波、Kobe波的计算结果具有相似结论，不再赘述)。综合考虑图30(a)～(c)，可认为剪切面积取5 m2(约为各层剪切面积的均值)时的减震效果较好，即在使用式(2)确定阻尼器投放量时，可根据计算的各层剪切面积平均值确定。

表6 10层结构应附加的阻尼器与结构刚度比

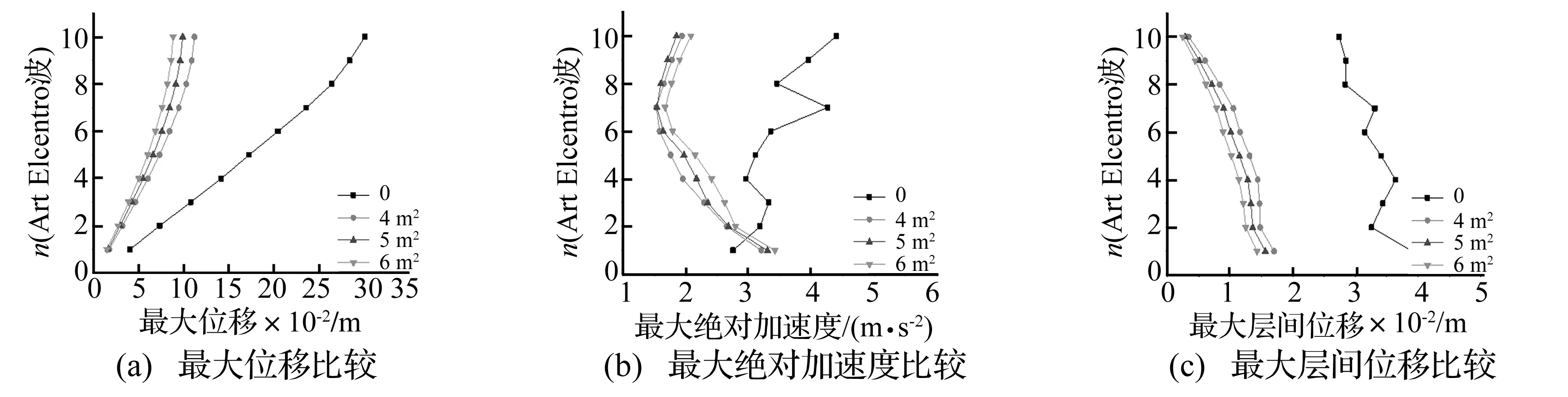
图30 10层结构不同阻尼器投放量的地震反应Fig.30 Seismic response of the 10 story structure with different dampers delivery

8 结 论

本文首先以附加黏弹性阻尼器的12层钢框架结构为研究对象，建立振动微分方程，并在此基础上考虑黏弹性阻尼器的减震作用，分别编制原结构与消能减震结构的弹塑性时程分析程序，分别计算四条不同地震动作用下，原结构与消能减震结构的地震反应，并通过计算对比两种结构的耗能情况。其次研究黏弹性阻尼器的不同布设方式以及不同黏弹层数对结构减震性能的影响，得出阻尼器投放量与楼层的相关性并进行验证结果表明：

(1) 附加黏弹性阻尼器后，结构各层的位移反应均有所减小，且峰值降低率可达25%以上；加速度反应、层间位移反应、剪力反应也均有不同程度的减小；黏弹性阻尼器可以减少位移和加速度，具有金属阻尼器和黏滞阻尼器的双重性质；

(2) 消能减震结构的结构本身消耗的各项能量占地震输入总能量的比例较原结构明显减小，阻尼器充分发挥减震性能，耗能可达地震输入能量的60%～70%，使得结构能够完全处于弹性阶段，不发生塑性变形，从而保护主体结构；

(3)通过对黏弹性阻尼器几种不同的布设工况以及黏弹性阻尼器不同投放量情况下的地震反应进行比较分析，得出针对12层钢框架结构的较优阻尼器投放量，据此总结出阻尼器与结构刚度比与结构层数的关系，式(2)。

(4) 为验证式(2)的正确性和通用性，对一10层钢框架结构的阻尼器投放量进行了计算，根据式(2)确定的阻尼器投放量能够使结构的减震效果达到较优的状态，故认为本文提出的方法具有一定的参考意义。

[1] 张敏. 建筑结构抗震分析与减震控制[M]. 成都：西南交通大学出版社, 2007：179.

[2] 周云，松本達治, 田中和宏,等. 高阻尼黏弹性阻尼器性能与力学模型研究[J]. 振动与冲击, 2015,34(7)：1-7.

ZHOU Yun, MATSUMOTO Tatsuji, TANAKA Kazuhiro, et al. Performance and mechanical model of high damping viscoelastic damps[J]. Journal of Vibration and Shock, 2015, 34(7)：1-7.

[3] 周颖，龚顺明，吕西林. 带黏弹性阻尼器钢结构振动台试验研究[J]. 建筑结构学报, 2014(7):1-10.

ZHOU Ying, GONG Shunming, LÜ Xilin. Study on shaking table testof a steel structure with additional viscoelastic dampers[J]. Journal of Architectural Structure, 2014(7):1-10.

[4] 谭小蓉. 黏弹性阻尼器在某框架结构减震中的研究[J]. 河南建材, 2014(1):19-21.

TAN Xiaorong. Study on viscoelastic dampers in the vibration of the frame structure [J]. Henan Building Materials, 2014(1):19-21.

[5] 桑超，刘中华. 黏弹性阻尼器在结构抗震控制中的应用[J]. 福建建筑, 2014(6):76-78.

SANG Chao, LIU Zhonghua. Viscoelastic dampers used in seismic control[J]. Fujian Architecture, 2014(6):76-78.

[6] 孙玉萍，王敏,王云. 钢框架中黏弹性阻尼器的空间布置优化分析[J]. 工程抗震与加固改造, 2008(5):29-32.

SUN Yuping, WANG Min, WANG Yun. Optimal analysis of spatial arrangement onsteel frame structure with viscoelastic dampers[J]. Earthquake Resistant Engineering and Retrofitting, 2008(5):29-32.

[7] 程文瀼，隋杰英，陈月明,等. 宿迁市交通大厦采用黏弹性阻尼器的减震设计与研究[J]. 建筑结构学报, 2000(3):30-35.

CHENG Wenrang, SUI Jieying, CHEN Yueming, et al. Design and research of viscoelastic dampers for traffic building in Suqian city[J]. Journal of Architectural Structure, 2000(3):30-35.

[8] 日本隔振构造协会. 被动减震结构设计施工手册[M]. 北京：中国建筑工业出版社, 2008： 35-38.

[9] 裴星洙. 建筑结构抗震分析与设计[M]. 北京：北京大学出版社，2013：86-102.

[10] 青山博之，上村智彦. マトリックス法による構造解析[M]. 東京：培風館, 2003.

[11] 裴星洙. 高层建筑结构设计[M]. 北京:知识产权出版社, 2014：322.

[12] 包世华. 新编高层建筑结构[M]. 北京：中国水利水电出版社, 2001：347.

[13] 笠井和彦, 所健. 黏弾性体の温度·振動数·振幅依存を考慮した構成則 (その2 温度上昇および歪·歪速度がもたらす非線形性のモデル化)[C]// 日本建築学会構造論文集, 第561号, 2002, 11： 55-63.

[14] 大熊 潔. アクリル系粘弾性体VEMの評価方法、パッシブ制振構造シンポジウム[M]. 東京工業大学長津田キャンパス, 2000: 249.

A study on seismic performance of steel frame structures with viscoelastic dampers

WEI Chuntong，PEI Xingzhu

(School of Civil Engineering and Architecture, Jiangsu University of Science and Technology，Zhenjiang 212000, China)

The structure without viscoelastic dampers was called as the original structure and the structure with viscoelastic dampers was called as energy dissipation structure. A 12-story steel frame structure model was established and its restoring force characteristic was calculated. The elastic plastic time history analysis program of two kinds of structures was coded. The seismic responses under a variety of earthquake actions were calculated and the energy distribution was compared. The viscoelastic dampers with different layout methods and delivery amount were investigated. The results show that the viscoelastic dampers have good shock absorption effect. The delivery amount can be determined according to the relevance to the structure to reach an optimum state.

viscoelastic damper; seismic response; energy allocation; dampers delivery

2013江苏省研究生创新计划立项配套(12508030012)

2015-07-30 修改稿收到日期：2015-10-10

魏春彤 女，硕士生，1991年4月生

裴星洙 男，博士，教授，1954年10月生

E-mail: peixingzhu@126.com

TU352

A

10.13465/j.cnki.jvs.2016.20.034