剪切来流下柔性圆柱体涡激振动响应试验研究

高 云, 付世晓, 熊友明, 杨家栋, 王盟浩

(1.西南石油大学 油气藏地质及开发工程国家重点实验室, 成都 610500;2. 上海交通大学 海洋工程国家重点实验室, 上海 200240)



剪切来流下柔性圆柱体涡激振动响应试验研究

高 云1, 2, 付世晓2, 熊友明1, 杨家栋1, 王盟浩1

(1.西南石油大学 油气藏地质及开发工程国家重点实验室, 成都 610500;2. 上海交通大学 海洋工程国家重点实验室, 上海 200240)

应用模型试验的方法，深入地研究了柔性圆柱体在剪切来流下的涡激振动响应。试验过程中通过旋转臂架从而形成相对剪切来流。通过测试得到的应变数据，基于模态叠加法得到圆柱体的涡激振动位移响应。研究结果表明：当折合速度较小时，响应频率会全程参加涡激振动；随着折合速度的上升，响应频率则会间歇性地参加涡激振动。涡激振动响应在横流方向仅存在一个锁定区域，而在顺流方向则存在两个锁定区域，其中第一个锁定区域与横流方向吻合。

剪切来流；柔性圆柱体；涡激振动；驻波；行波；锁定区域

圆柱体在一定的来流下，会在其两侧形成交替的漩涡，漩涡脱落会产生周期性的横向(Cross-Flow, CF)升力以及流向(In-Line, IL)拖曳力。若圆柱体为弹性支撑，周期性的升力以及拖曳力会引起圆柱体横向以及流向发生振动，称之为涡激振动(Vortex-Induced Vibration, VIV)[1]。为了揭示涡激振动的机理特性，康庄等[2-10]对小细长比(小于100)刚性圆柱体的涡激振动响应进行了研究。随着海洋油气开发逐步向深海以及极深海水域发展，大细长比柔性立管逐渐在深水工程中出现，而大细长比柔性立管涡激振动所表现出的细长柔性圆柱体特性与刚性圆柱体特性有着本质的区别。为了满足深水立管工程的发展需求，黄维平等[11-13]针对细长柔性圆柱体的涡激振动响应特性展开了大量的研究。但是这些研究所考虑的来流大多是均匀流剖面，而实际海洋真实环境中，海水的流速并不是均匀分布的，而是流速随着海水深度的变化呈现剪切分布特性。为了更切合实际地研究真实海洋工程中的柔性立管的涡激振动响应特性，需要对剪切流场中的细长柔性圆柱体的涡激振动响应特性加以研究。表1给出了近10多年国内外关于剪切流场中柔性圆柱体涡激振动响应的试验方法研究[14-19]、半经验模型方法研究[20]以及计算流体动力学(Computational Fluid Dynamics, CFD)方法研究[21-22]。

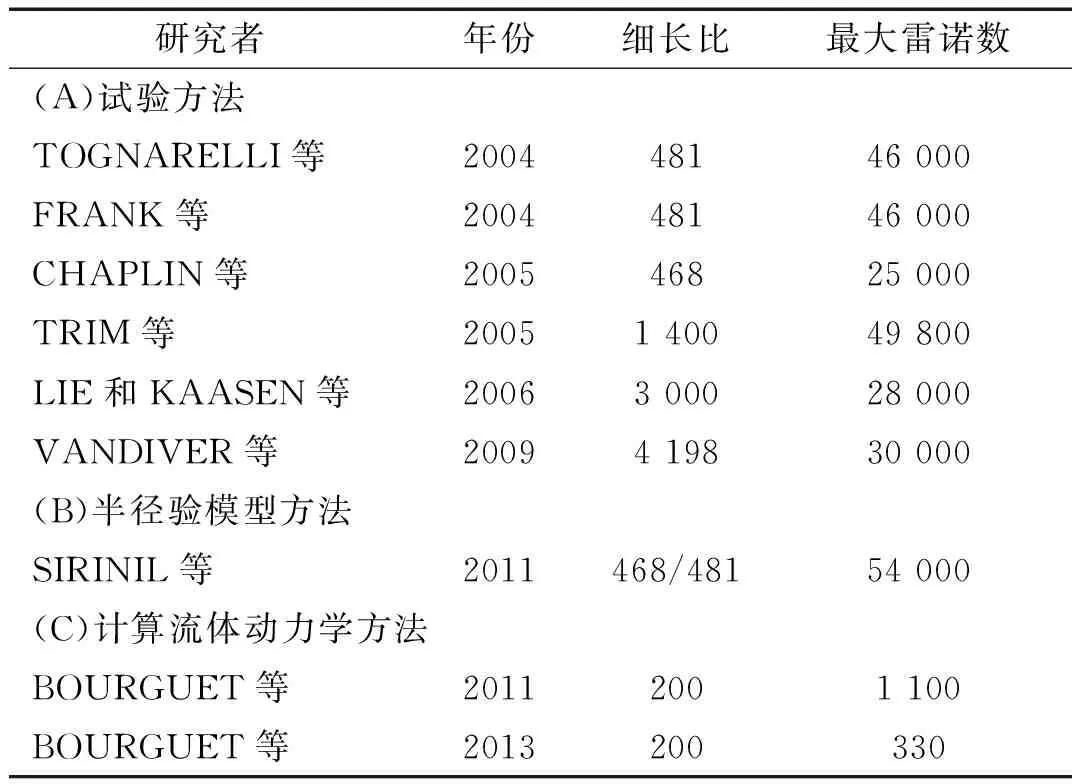
表1 剪切流下柔性圆柱体涡激振动响应研究

从目前的国内外研究现状来看，针对剪切来流下柔性圆柱体的涡激振动响应，尚存在很多问题需要进行更为深入的研究。比如：① 剪切流场中，柔性圆柱体的涡激振动响应特性表现为驻波特性还是行波特性？随着Re数的增加，驻波成分和行波成分又将发生怎样的变化？② 对于均匀流下的细长柔性圆柱体，涡激振动的IL方向的响应频率通常是CF方向的2倍，而对于剪切来流，柔性圆柱体在IL以及CF方向涡激振动的响应频率是否存在同样的关系？③ 剪切流场中，随着Re数的上升，整个流剖面会逐渐变得不稳定，从而表现出明显的湍流特性。此时涡激振动响应频率不再是稳定不变的，而是随时间发生变化，振动频率又是怎样随时间发生变化的？

基于以上问题，本文将在第4部分(分析与讨论部分)分两小节对此进行了研究。研究内容如下：在4.1节部分，研究了不同折合速度的剪切流场中柔性圆柱体的涡激振动响应无量纲振幅比特性，包括无量纲振幅比沿圆柱体轴线分布的特性以及最大无量纲振幅比随折合速度的变化关系，并在此基础上进一步研究了剪切流场中柔性圆柱体涡激振动响应的驻波与行波特性。在4.2节部分，研究了柔性圆柱体涡激振动响应主导频率随折合速度的变化关系，紧接着进一步研究了两种典型折合速度下的圆柱体涡激振动位移响应频率随时间变化的特性。

1 试验装置介绍

如图1所示，试验中剪切来流的模拟方法是将柔性圆柱体的一端固定在垂直的固定圆柱上，另一端在旋转臂架的带动下进行旋转运动，从而使得柔性圆柱体和流场之间形成相对的线性剪切来流。由图1可以看出：剪流流场中最大流速分布在圆柱体顶部与旋转臂架连接的端点，最小流速分布在圆柱体底部与竖直固定柱体连接的端点，沿圆柱体长度方向呈线性剪切分布。

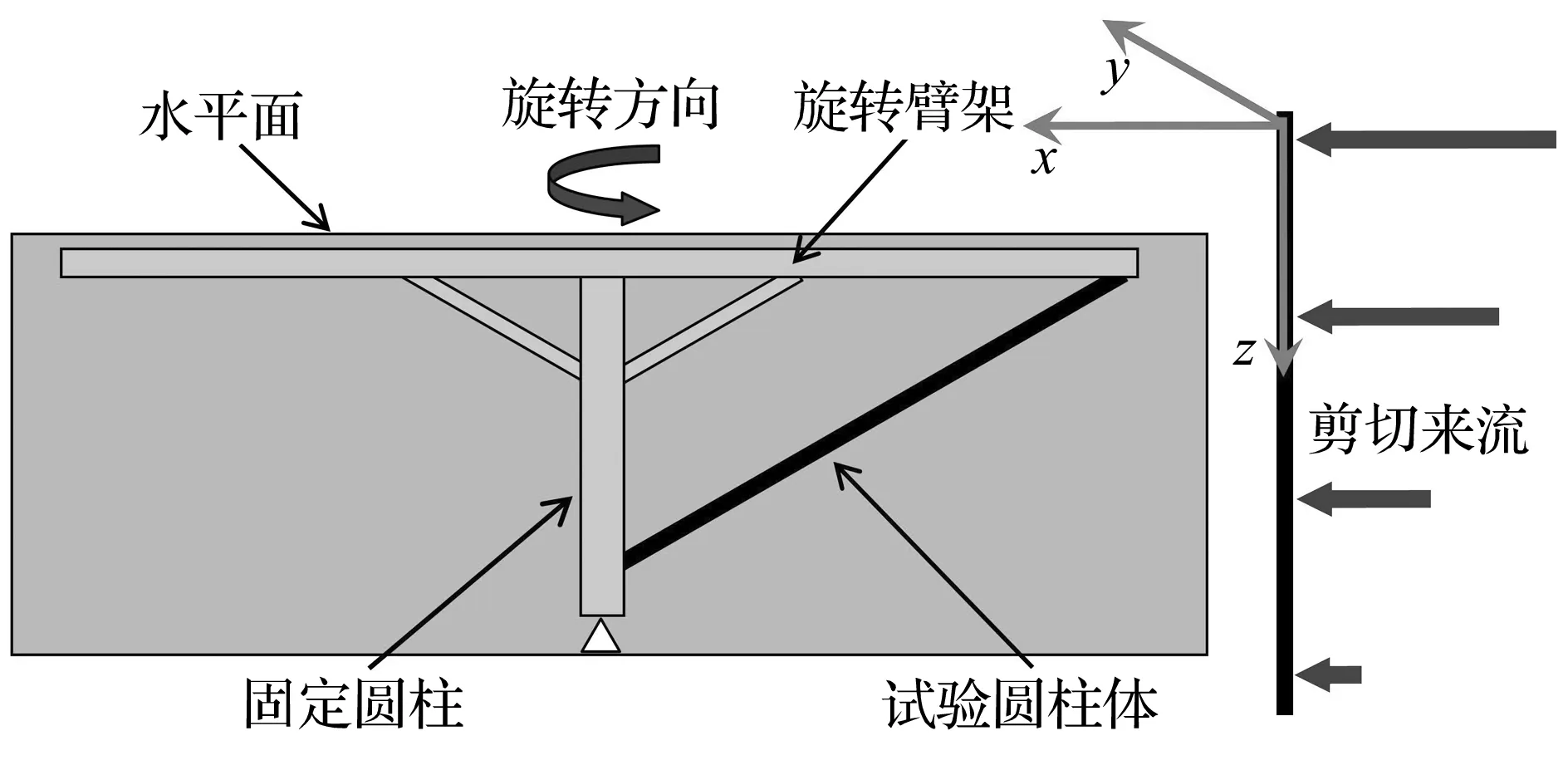
图1 试验装置示意图Fig.1 Sketch of the device during the experiment

柔性圆柱体模型的长度为6.75 m，外径为0.03 m。试验采用11种流速工况，对应的圆柱体顶端最大流速分别为0.5～4.5 m/s。圆柱体的其它试验参数见表2。

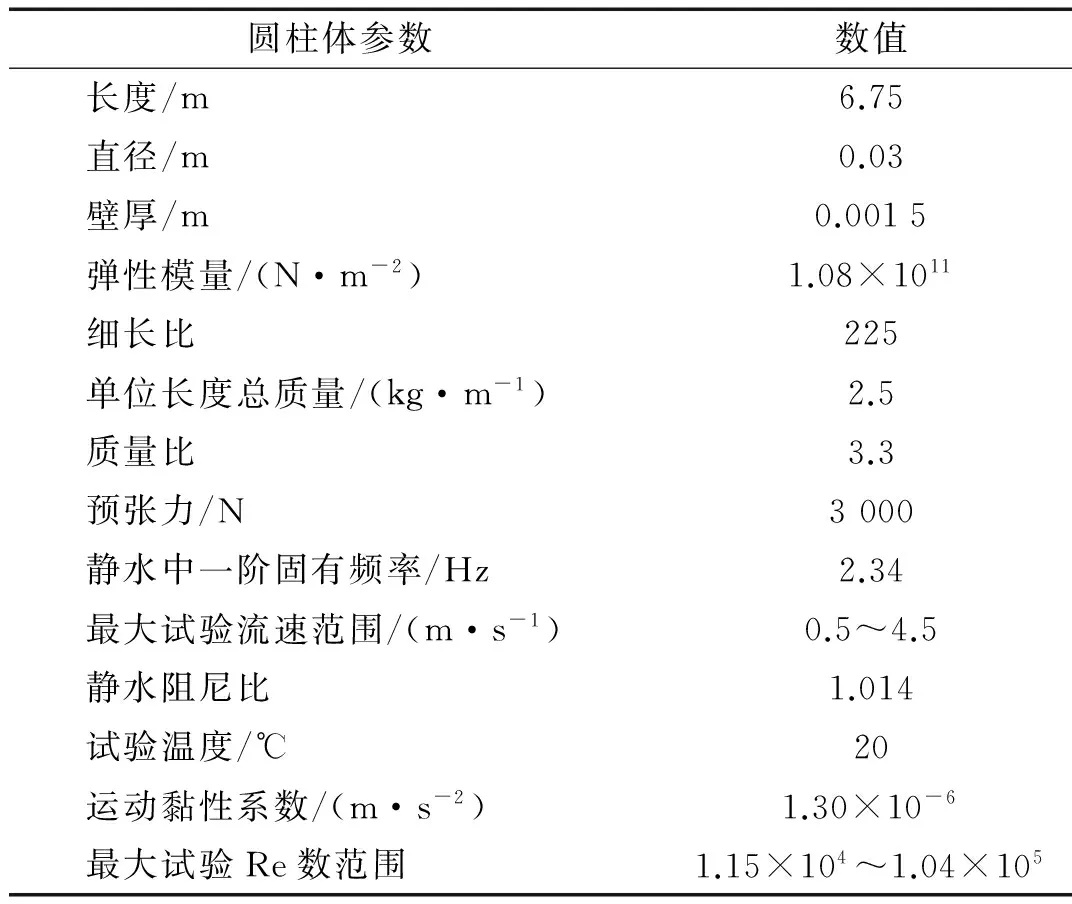
表2 圆柱体试验参数

试验中圆柱体模型共采用88个光纤光栅应变传感器，分别布置于CF1、CF2、IL1以及IL2四个方向(如图2所示)。CF每个方向布置19个传感器，记为G01-G19；IL每个方向布置25个传感器，记为F01-F25。通过图2中的应变片测试得到应变，再依据模态叠加法便可计算得到每个应变片点对应的位移响应。

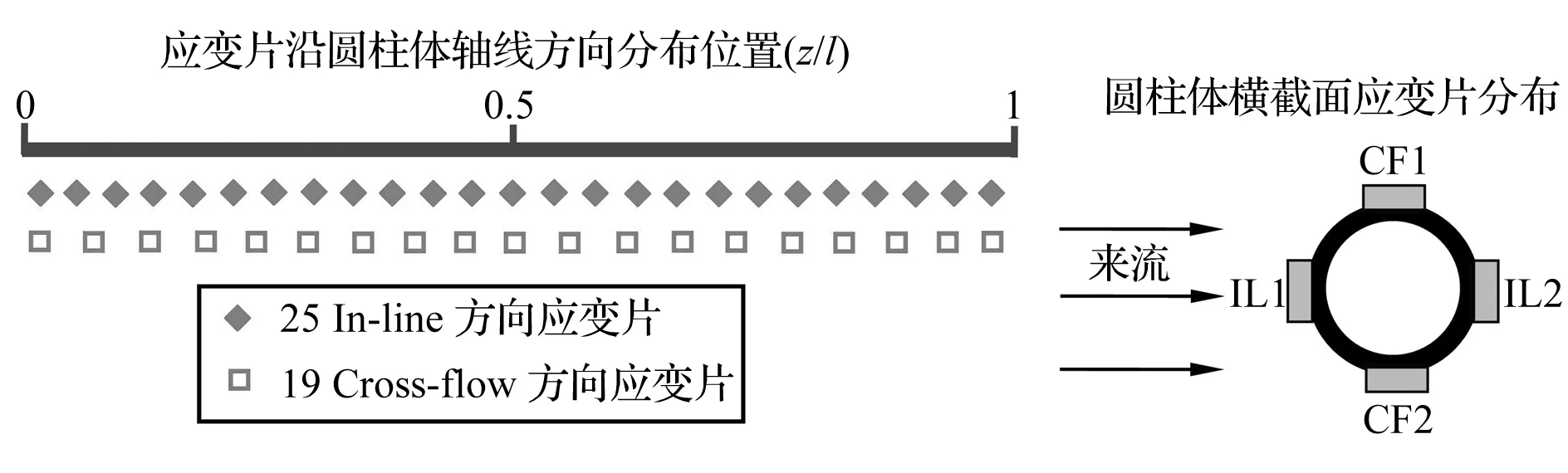
图2 应变片分布位置示意图Fig.2 Sketch of the strain sensor locations

2 数据分析方法

圆柱体发生涡激振动时，由于圆柱体的周期振动，圆柱体的轴向张力会发生周期性的变化，这使得测量的应变信号包括两部分：由初始张力产生的轴向应变以及由涡激振动产生的轴向应变。而由预张力产生的应变需要进行消除。如图2所示，CF1和CF2相互对称，因此由VIV产生的弯曲应变大小相等，方向相反，而轴向力产生的应变是相同的，因此CF1和CF2处的应变可表示为：

εCF1=εVIV-CF+εT

εCF2=-εVIV-CF+εT

(1)

对上式进行简单的变换，便可得到CF方向的由VIV引起的弯曲应变为：

(2)

IL方向则与CF方向情况不同，主要是由于IL方向在初始拖曳力的作用下，圆柱体会在流向产生一个初始的弯曲应变initial，因此测试应变包括三个部分：由初始张力产生的应变、由初始拖曳力产生的应变以及由VIV产生的轴向应变。因此IL1和IL2处的应变可表示为：

εIL1=εinitial+εVIV-IL+εT

εIL2=-εinitial-εVIV-IL+εT

(3)

为了计算式(3)，需要引入2个假设。如果试验选取的稳定段时间足够长，可认为VIV引起的弯曲应变的时间历程均值为零，引入假设1，表示如下：

(4)

IL方向初始拖曳力引起的初始应变的变化只可能由拖车速度发生略微的波动所导致，但是我们拖车速度的精确度达到了0.2%，因此可以引入假设2，假设初始应变不随时间发生变化，则可表示如下：

(5)

由式(3)，可以得到：

(6)

对式(6)两边进行时间平均，并结合式(4)可得到：

(7)

综合考虑式(5)～式(7),可得到IL方向由VIV产生的弯曲应变为：

评定两组术后髋关节的恢复情况,采用Harris髋关节评分法,满分100分,90分以上为优、80-89分为良、70-79分为中,70分以下为差。

(8)

假设受轴向力作用的圆柱体做微小变形的振动，则CF和IL方向的响应均可基于模态叠加法表示为：

(9)

式中，φi(z)为圆柱体的第i阶模态振型，pi(t)为圆柱体的第i阶模态位移权重，z为圆柱体的位置，基于小变形假设，圆柱体的曲率可表示为圆柱体位移响应对空间求二次导数，如下：

(10)

式中，φi(z)为圆柱体的第i阶模态曲率，圆柱体的曲率和弯曲应变之间的关系，可表示为：

(11)

式中，R为圆柱体的外部半径，由式(10)和式(11)可以看出：给定了测点的应变可求出对应的模态权重，进一步可根据式(9)便可以求出位移响应。本文试验的圆柱体模型可以简化为两端铰接的索模型，因此第i阶模态振型可写成：

(12)

将式(12)代入式(10)得到：

(13)

式中:ui(t)为第i阶模态曲率权重，可表示为：

(14)

结合式(11)和式(13)，得到：

(15)

式中:ei(t)为第i阶应变模态权重，可写成：

(16)

3 分析与讨论

在后续的分析中，我们对剪切流剖面的最大流速V进行了无量纲化，引入折合速度，定义如下：

(17)

式中:V为流剖面的最大流速，D为圆柱体外径，f1为圆柱体在水中的一阶固有频率，可由下式计算得到：

(18)

实际式(18)中F(t)是随时间在预张力附近发生变化的，这里为数据处理方便，此处F(t)取为预张力3 000 N，为定值。m为单位长度振动系统质量，包括：圆柱体结构质量、内部流体质量以及附加质量。这里在计算附加质量时所采用的附加质量系数为1.0，l为圆柱体长度，E为弹性模量，I为圆柱体的惯性矩，这些参数均可由表2获得，n为圆柱体固有频率的阶数。经过式(2)计算得到圆柱体的一阶固有频率为2.34 Hz，已知圆柱体的一阶固有频率、圆柱体直径以及最大流速，便可根据式(17)计算得到11种最大流速对应的11种折合速度以及Re数，如表3所示。

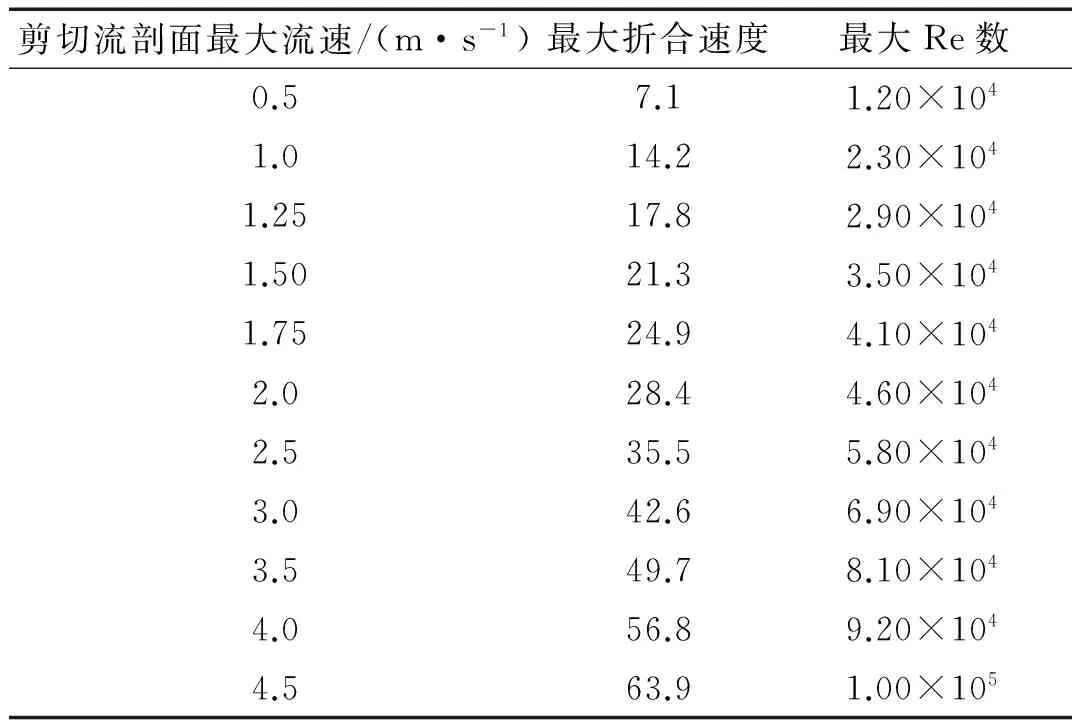
表3 最大流速对应的折合速度以及Re数

这里为了进一步验证圆柱体固有频率计算的可靠性，采用了试验方法对圆柱体在水中的真实固有频率进行了研究。通过对水中圆柱体中点处的应变时间历程做快速傅里叶变换(Fast Fourier Transform, FFT)，便可得到圆柱体的真实固有频率。如图3所示，给出了水中圆柱体中点处的应变时历曲线以及应变幅值谱，由图可以看出经试验测试得到的一阶固有频率为2.41 Hz，与计算固有频率2.34 Hz非常接近。

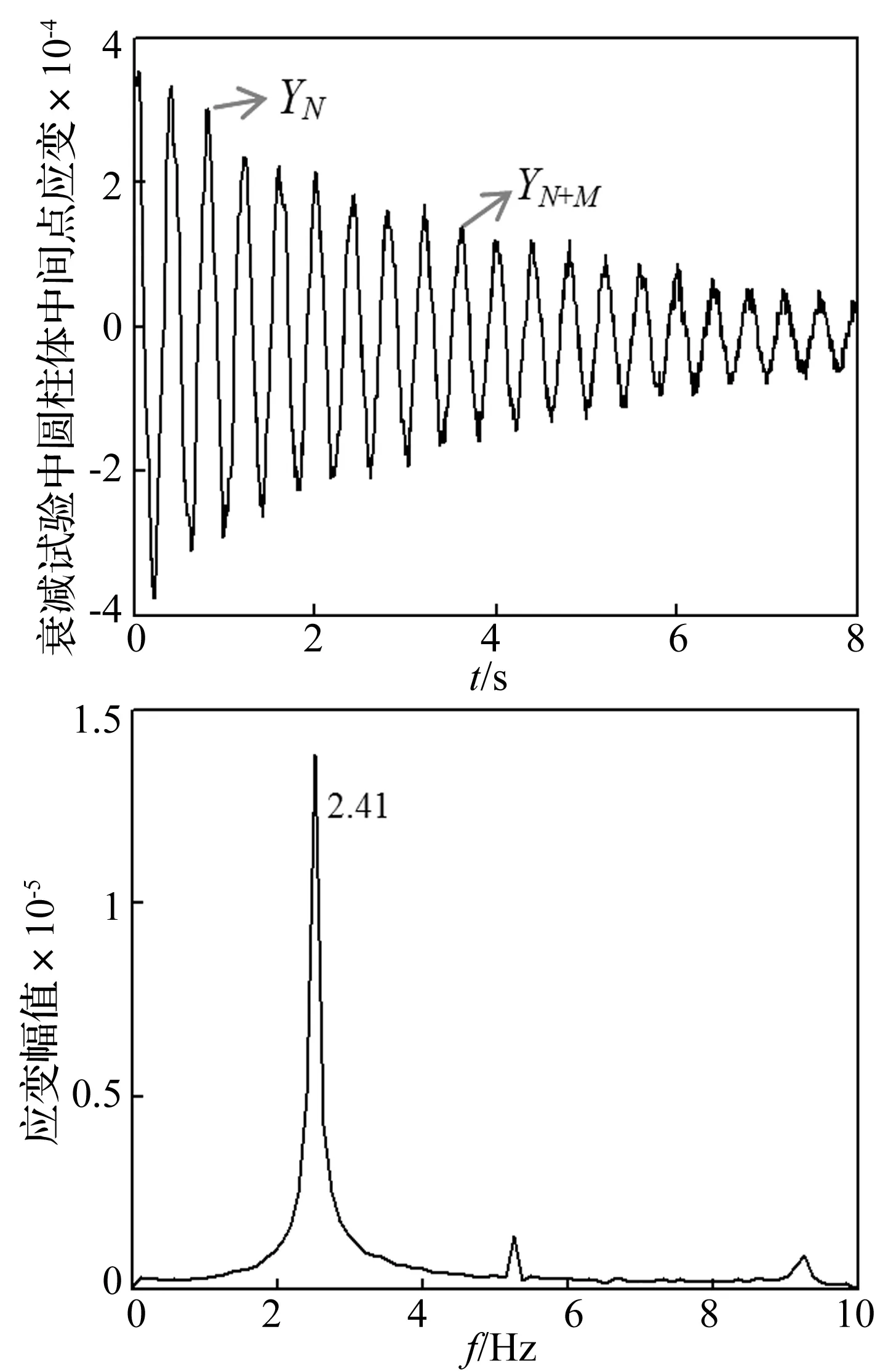
图3 衰减试验中圆柱体中点处的应变时间历程曲线以及应变幅值谱Fig.3 Time trace and amplitude spectrum of the CF strain at midpoint during free decay test

图3同样给出了圆柱体中点处第N个以及N+M个圆柱体的应变幅值，便可根据下式计算得到圆柱体在水中的阻尼比。

(19)

经计算得到的水中阻尼比为0.014，如表2所示。在后续的研究中，会用到柔性圆柱体的前5阶静水固有频率，这里依次给出，如表4所示。

表4 静水中圆柱体的前5阶固有频率

3.1 圆柱体涡激振动位移响应分析

如图1所示建立直角坐标系，坐标原点设在流剖面最大流速的圆柱体上端点，z方向为沿圆柱体上端点指向下端点；x方向为流速方向，即圆柱体涡激振动的IL方向；根据右手坐标系准则，y方向即为涡激振动的CF方向。

图4给出了CF以及IL方向不同折合速度下的最大无量纲振幅比。由图4可以看出：CF方向的最大响应位移约为0.9D，出现在折合速度21.3时；IL方向的最大响应位移为0.35D, 出现在折合速度56.8时；CF方向的响应位移随着折合速度的增加呈现先上升再减小的趋势，随着折合速度的进一步增加，CF方向的最大响应位移基本稳定在0.30D附近。IL方向的响应位移随着折合速度的增加，呈现上升下降再上升的变化趋势，最后稳定在0.35D附近。由图4同样可以看出：CF方向仅存在一个峰值区域，分布在折合速度21.3附近；而IL方向则存在两个峰值区域，分别分布在折合速度为21.3以及56.8附近，因此可以判断出：CF方向仅存在1个锁定区域，而IL方向则存在2个锁定区域，且IL方向的第一个锁定区域与CF方向吻合。

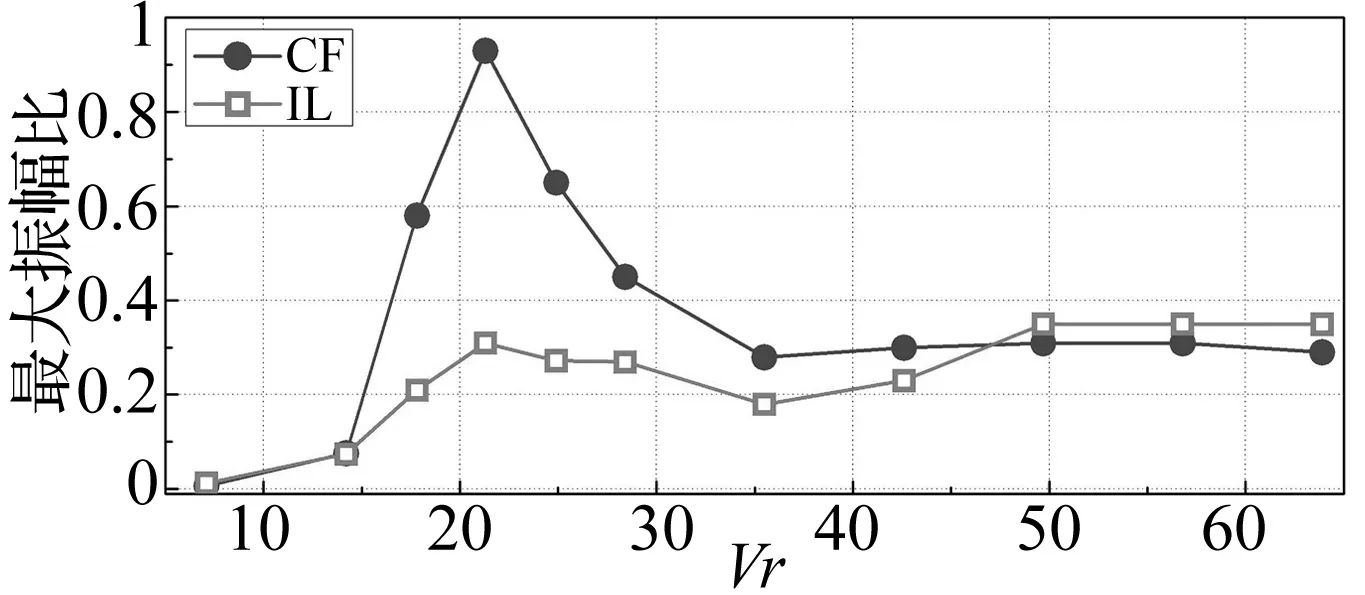
图4 不同折合速度下CF以及IL方向最大振幅比Fig.4 Maximum non-dimensional displacements in CF and IL directions at various reduced velocities

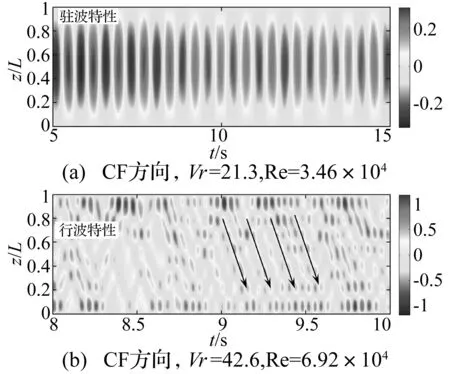
图5 两种不同折合速度下CF方向圆柱体的位移响应变化云图Fig.5 Time series of CF displacement fluctuation along the cylinder model at two different reduced velocities

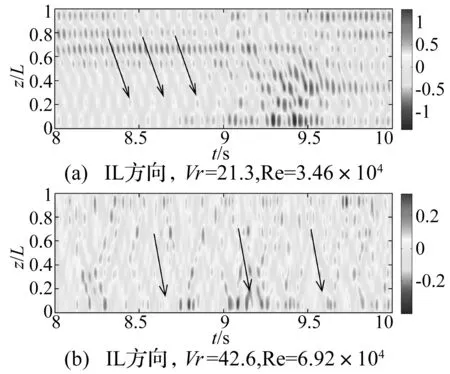
图6 两种不同折合速度下IL方向圆柱体的位移响应变化云图Fig.6 Time series of IL displacement fluctuation along the cylinder model at two different reduced velocities

图5以及图6进一步给出了两种典型折合速度(21.3以及42.6)对应的CF以及IL方向圆柱体的涡激振动响应位移变化云图。由图5可以看出：随着折合速度的上升，CF方向的涡激振动响应逐步从驻波主导变为行波主导。由图6可以看出：当折合速度超过21.3时，IL方向的涡激振动响应几乎全部为行波成分。

3.2 圆柱体涡激振动频率响应分析

图7给出了不同折合速度下剪切流场中柔性圆柱体在CF以及IL方向沿轴线方向最大响应位移处的主导频率以及根据斯脱哈尔规律(fst=St×V/D)计算得到的斯脱哈尔频率。

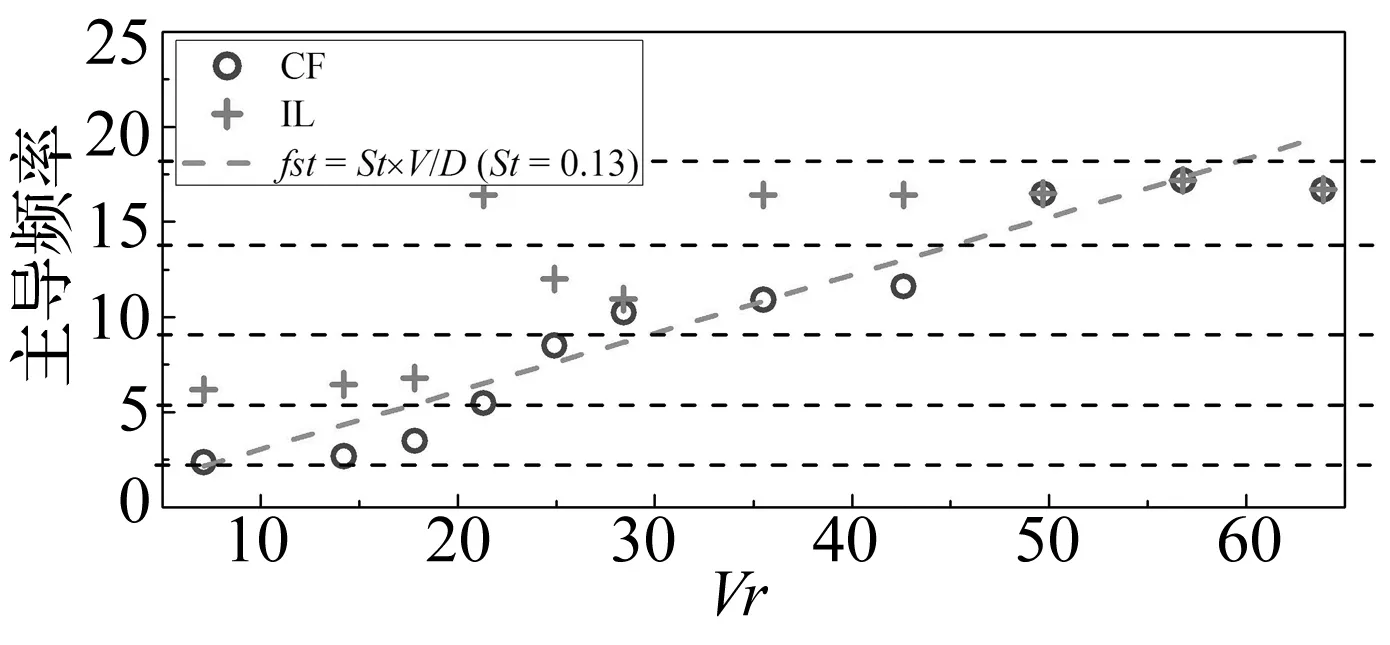
图7 圆柱体主导频率以及斯脱哈尔频率Fig.7 Dominant frequencies of cylinder and Strouhal frequencies

通过对11种不同折合速度的分析，我们可以发现剪切来流中CF方向主导频率、IL方向主导频率以及斯脱哈尔频率之间的关系与均匀流中相比有着很大的区别：① 均匀流中IL方向的主导频率通常大致是CF方向的2倍；但是剪切流中IL方向和CF方向的主导频率不再存在大致的2倍关系。② 均匀流中CF方向的主导频率通常呈线性增长趋势分布在fst=St×V/D附近；而对于剪切流，CF方向的主导频率虽然仍然出现在斯脱哈尔漩涡泄放频率附近，但是并没有随着折合速度的增加而呈线性增加趋势，却呈现出明显的分段特性：如当折合速度为7.1和14.2时，CF方向的主导频率分布在1阶固有频率2.34 Hz附近；当折合速度为21.3时，CF方向的主导频率分布在2阶固有频率5.05 Hz附近，对比图4中的振幅可以看出此时CF方向的位移得到了最大值，由于与2阶固有频率吻合，我们称之为 “二阶锁定”。随着折合速度的进一步上升，CF方向的主导频率依次分布在3阶、4阶以及5阶固有频率附近。

图8给出了Vr=21.3时柔性圆柱体在CF以及IL方向的涡激振动位移响应频率随时间变化的特性。由图10可以看出：① CF方向两个不同测点处的主导频率相等，均为5.5 Hz；z/L=0.181处位移响应频率为单模态，而z/L=0.500处位移响应频率则呈现明显的多模态，除了主导频率5.5 Hz外，还存在另外一个2倍于主导频率的峰值频率10.94 Hz。② IL方向两个不同测点处的位移响应频率均具有明显的多模态特性，且不同测点处的主导频率不同：z/L=0.181处的主导频率为5.5 Hz；而z/L=0.500处的主导频率为16.43 Hz，约为5.5 Hz的3倍。③ 无论是CF方向还是IL方向，不同测点位置处的位移响应频率能量分布均非常集中，即：频率沿时间呈直线分布，不随时间发生变化。

图9给出了Vr=42.6时柔性圆柱体在CF以及IL方向的涡激振动位移响应频率随时间变化的特性。将图9与图8进行综合对比分析，可以得到：① 与折合速度较低的Vr=21.3的位移频率-时间特性相比，Vr=42.6时圆柱体的位移响应频率能量分布的更为分散，即：峰值频率沿时间呈一定程度的振荡分布。表现为：Vr=21.3时涡激振动响应频率为窄带分布，而Vr=42.6时涡激振动响应频率则为宽带分布。② 对比图8，Vr=21.3时涡激振动响应频率全程参加涡激振动响应过程，即：响应频率在时历上呈连续分布形式；而Vr=42.6时涡激振动响应频率则间歇性地参加涡激振动响应过程，即：响应频率在时历上断断续续地分布。

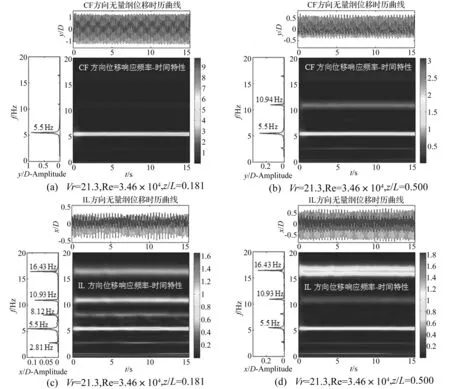
图8 Vr = 21.3时CF以及IL方向两个不同测点位置处的涡激振动位移响应频率-时间特性分析Fig.8 Time-frequency analysis at two different sensor locations in both CF and IL directions for the case Vr = 21.3

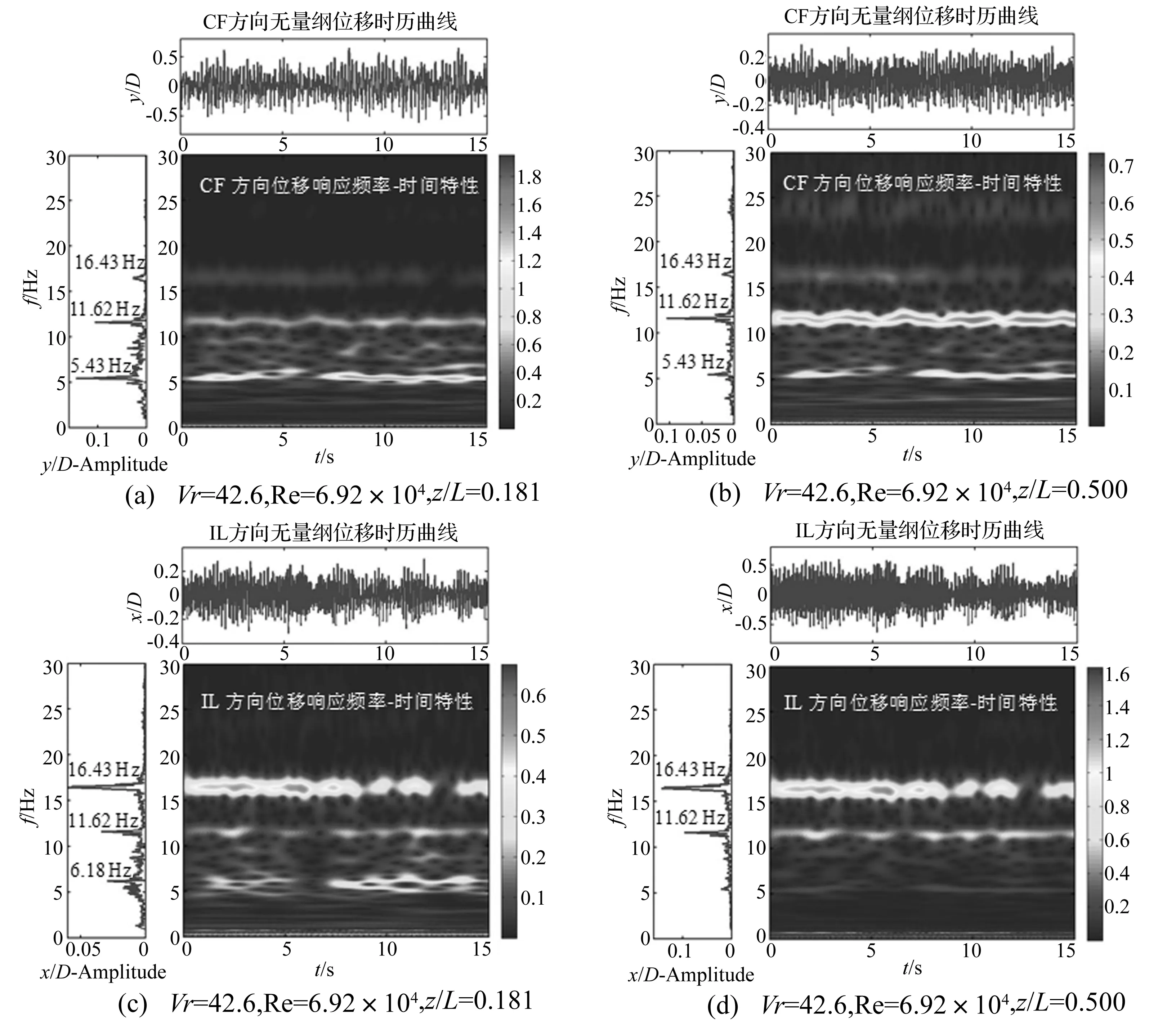
图9 Vr = 42.6时CF以及IL方向两个不同测点位置处的涡激振动位移响应频率-时间特性分析Fig.9 Time-frequency analysis at two different sensor locations in both CF and IL directions for the case Vr = 42.6

4 结 论

本文针对柔性圆柱体在剪切来流下的涡激振动响应特性进行了试验研究，特性参数包括位移响应特性以及频率响应特性，通过以上研究可得到如下结论：

(1) 柔性圆柱体的CF方向以及IL方向的最大响应位移分别为0.90D和0.35D，分别位于折合速度为21.3以及56.8处。随着折合速度的增加，CF方向以及IL方向的涡激振动响应分别稳定在0.30D以及0.35D附近。

(2) 随着折合速度的增加，柔性圆柱体涡激振动响应呈现出上升下降稳定的分布趋势，CF方向仅存在一个锁定区域；而IL方向的涡激振动响应随着折合的增加呈现出上升下降再上升稳定的分布趋势，因此，IL方向存在两个锁定区域。

(3) 当折合速度较低时，涡激振动响应频率能量分布非常集中，且响应频率全程参加涡激振动；随着折合速度的上升，涡激振动响应频率能量分布逐渐呈现分散趋势，且响应频率不会全程参加振动而是间歇性地参加振动。

[1] BLEVINS R D. Flow-induced vibration [M]. 2nd ed. Malabar, FL: Krieger Publishing Inc, 2001.

[2] 康庄, 贾鲁生. 圆柱体双自由度涡激振动轨迹的模型试验 [J]. 力学学报, 2012, 44(6): 970-980.

KANG Zhuang, JIA Lusheng. An experimental investigation on VIV trajectories of a two degree free vibration cylinder [J]. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(6): 970-980.

[3] 王海青, 郭海燕, 刘晓春, 等. 海洋立管涡激振动抑制方法试验研究 [J]. 中国海洋大学学报, 2009, 39(增刊1): 479-482.

WANG Haiqing, GUO Haiyan, LIU Xiaochun, et al. Experimental investigation of vortex-induced vibration suppression of marine riser [J]. Periodical of Ocean University of China, 2009, 39(Sup1): 479-482.

[4] SARPKAYA T. Vortex-induced oscillations [J]. Journal of Applied Mechanics-ASME, 1979, 46: 241-258.

[5] GRIFFIN O M, RAMBERG S E. Some recent studies of vortex shedding with application to marine tubulars and risers [J]. Journal of Energy Resources Technology-ASME, 1982, 104: 2-13.

[6] BEARMAN P W. Vortex shedding from oscillating bluff bodies [J]. Annual Review of Fluid Mechanics, 1984, 16: 195-222.

[7] PARKINSON G V. Phenomenon and modelling of flow-induced vibrations of bluff bodies [J]. Progress in Aerospace Sciences, 1989, 26: 169-224.

[8] SARPKAYA T. A critical review of the intrinsic nature of vortex-induced vibrations [J]. Journal of Fluids and Structures, 2004, 19: 389-447.

[9] WILLIAMSON C H K, GOVARDHAN R. Vortex-induced vibrations [J]. Annual Review of Fluid Mechanics, 2004, 36: 413-455.

[10] WILLIAMSON C H K, GOVARDHAN R. A brief review of recent results in vortex-induced vibrations [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96: 713-735.

[11] 黄维平, 曹静, 张恩勇, 等. 大柔性圆柱体两自由度涡激振动试验研究 [J]. 力学学报, 2011, 43(2): 436-440.

HUANG Weiping, CAO Jing, ZHANG Enyong, et al. On vortex induced vibration in two-degree-of-freedoms of flexible cylinders [J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(2): 436-440.

[12] 姚宗, 陈刚, 杨建民, 等. 流速分层流场中细长柔性立管涡激振动试验研究 [J]. 上海交通大学学报, 2009, 43(8): 1273-1279.

YAO Zong, CHEN Gang, YANG Jianmin, et al. Experimental investigation on vortex induced vibration of a long flexible riser in a stepped current [J]. Journal of Shanghai Jiaotong University, 2009, 43(8): 1273-1279.

[13] 高云，付世晓，宋磊建. 柔性立管涡激振动抑制装置试验研究 [J], 振动与冲击，2014，33(14): 77-83.

GAO Yun, FU Shixiao, SONG Leijian. Experimental investigation on the suppression device of VIV of a flexible riser [J]. Journal of Vibration and Shock, 2014, 33(14): 77-83.

[14] TOGNARELLI M A, SLOCUM S T, FRANK W R, et al. VIV response of a long flexible cylinder in uniform and linearly sheared currents [C]// Offshore Technology Conference. Houston, TX, 2004.

[15] FRANK W R, TOGNARELLI M A, SLOCUM S T, et al. Flow-induced vibration of a long, flexible, straked cylinder in uniform and linearly sheared currents [C]// Offshore Technology Conference. Houstom, TX, 2004.

[16] CHAPLIN J R, BEARMAN P W, HUERA-HUARTE F J, et al. Laboratory measurements of vortex-induced vibrations of a vertical tension riser in a stepped current [J]. Journal of Fluids and Strucutres, 2005, 21: 3-24.

[17] TRIM A D, BRAATEN H, LIE H, et al. Experimental investigation of vortex-induced vibration of long marine risers [J]. Journal of Fluids and Structures, 2005, 21: 335-361.

[18] LIE H, KAASEN K E. Modal analysis of measurements from a large-scale VIV model test of a riser in linearly sheared flow [J]. Journal of Fluids and Structures, 2006, 22: 557-575.

[19] VANDIVER J K, JAISWAL V, JHINGRAN V. Insights on vortex-induced, travelling waves on long riser [J]. Journal of Fluids and Structures, 2009, 25: 641-653.

[20] SRINIL N. Analysis and prediction of vortex-induced vibrations of variable-tension vertical risers in linearly sheared currents [J]. Applied Ocean Research, 2011, 33: 41-53.

[21] BOURGUET R, KARNIADAKIS G E, TRIANTAFYLLOU M S. Lock-in of the vortex-induced vibrations of a long tensioned beam in shear flow [J]. Journal of Fluids and Structures, 2011, 27: 838-847.

[22] BOURGUET R, KARNIADAKIS G E, TRIANTAFYLLOU M S. Multi-frequency vortex-induced vibrations of a long tensioned beam in linear and exponential shear flows [J]. Journal of Fluids and Structures, 2013, 41: 33-42.

Experimental study on vortex induced vibration responses of a flexible cylinder in sheared current

GAO Yun1,2, FU Shixiao2, XIONG Youming1, YANG Jiadong1, WANG Menghao1

(1. State Key Laboratory of Oil and Gas Reservoir Geology and Exploration, Southwest Petroleum University, Chengdu 610500, China; 2. State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)

The vortex induced vibration responses of a flexible cylinder in sheared current were studied experimentally. The relative sheared currents were simulated by rotating the cantilever in the experiment. Based on the modal analysis method, the displacement responses could be obtained by the measured strain. The results indicate that the response frequency involves in the vibration all the time at low reduced velocity. However, at high reduced velocity, response frequency involves in the vibration intermittently. Vortex induced vibration response has only one lock-in region in the CF direction, but two lock-in regions in the IL direction. The first lock-in region in the IL direction coincides with the lock-in region in the CF direction.

sheared current; flexible cylinder; vortex induced vibration; standing wave; travelling wave; lock-in region

国家自然科学基金重大项目(51490674); 国家自然科学基金面上项目(51279101); 西南石油大学青年教师 “过学术关” 基金(201499010114); 西南石油大学科研启航计划资助项目(2015QH2005)

2015-06-02 修改稿收到日期：2015-08-08

高云 男，博士后, 讲师，硕士生导师，1985年生

付世晓 男，研究员, 博士生导师，1976年生

E-mail: shixiao.fu@sjtu.edu.cm

O357

A

10.13465/j.cnki.jvs.2016.20.023