输电导线气动阻尼效应的风洞试验研究

王述良， 梁枢果， 邹良浩， 汪大海

(1.武汉大学 土木建筑工程学院，武汉 430072；2.武汉理工大学 土木工程与建筑学院，武汉 430070)



输电导线气动阻尼效应的风洞试验研究

王述良1， 梁枢果1， 邹良浩1， 汪大海2

(1.武汉大学 土木建筑工程学院，武汉 430072；2.武汉理工大学 土木工程与建筑学院，武汉 430070)

基于单跨六分裂输电导线气弹模型风洞试验，测得了不同风速下输电导线端部，即输电导线传递给输电塔的动张力时程，结合经验模态分解法(EMD)、小波分析及随机减量法(RDT)识别了输电导线的前四阶气动阻尼比，并将其与基于准定常理论的气动阻尼比进行了对比。考虑气动阻尼的影响，对输电导线动张力进行了计算。研究结果表明：输电导线的气动阻尼相对于结构阻尼，占有主导地位，在强风下可以达到结构阻尼比的10倍以上；由于输电导线的风致非线性振动，使得基于准定常理论的气动阻尼比与识别结果相比存在显著差异；强风作用下，不考虑气动阻尼比的计算结果将严重地高估输电导线的风致动张力响应。

风洞试验；气弹模型；气动阻尼；输电导线；风致响应

输电导线是送电线路的重要组成部分，其结构的安全性直接关系到整个送电系统的正常运行，随着用电需求地不断增大，长距离送电已经越来越多的应用到实际工程中，输电导线的档距也相应地不断增大，使得其对风荷载的作用更为敏感，由于输电导线风致振动的强非线性，在风荷载作用下，其风致振动机理十分复杂，气弹效应特别是气动阻尼效应的影响不可忽略[1-2]。METHA等[3-4]通过实测数据证实了作用于输电塔上的导地线的强气动阻尼力，在强风作用下，输电导线的几何非线性和附加的气动阻尼力对输电塔的作用十分明显。因此，准确的考虑气动阻尼对输电导线风致响应的影响是进行输电线路精细化设计的重要基础。尽管，对于整个输电线路气弹效应的研究已经受到较为广泛的关注。TAKEUCHI等[5]运用两个实际输电塔的实测数据，进行了输电塔的气动阻尼比识别，分析了输电塔气动阻尼比随风速及频率的变化规律。任坤等[6]通过风洞试验数据进行了输电塔线体系气动阻尼比识别。邹良浩等[7]识别了输电塔在挂线和不挂线情况下各阶振型结构阻尼比和气动阻尼比，分析输电塔在挂线和不挂线情况下结构阻尼比和气动阻尼比的变化规律。段成荫等[8]采用特征系统实现算法(ERA)对输电塔风洞试验结果进行了包括气动阻尼在内的模态参数识别。楼文娟等[9]针对连续多跨输电线路在瞬态风场作用下的风偏问题，提出考虑气动阻尼效应的输电线路风偏动态分析方法,结果表明输电线路气动阻尼对风偏动态响应影响显著。对于输电导线气动阻尼及其对传递给塔架的风致动张力影响的研究却鲜有所见，然而了解输电导线的气动阻尼，进而精确计算输电导线传递给塔架的荷载是了解塔线耦合振动特性及进行解耦分析的重要基础。

鉴于此，本文进行了典型六分裂输电导线全跨缩尺气弹模型风洞试验，测得了其端部动张力即传递给塔架的荷载，并基于动张力时程，结合运用EMD,小波分析以及随机减量技术识别气动阻尼:首先通过EMD对振动信号进行分解，进一步运用小波分析消除频率混叠的影响，最后运用RDT进行气动阻尼识别，使得识别结果更为稳定;并将识别结果与基于准定常理论计算结果进行了对比分析。此外，基于输电导线动张力计算模型，分析了考虑与不考虑气动阻尼对输电导线风致动张力的影响。

1 风洞试验方案

1.1 气弹模型设计与制作

根据相似理论，设计了原型为JL/G3A-1000/45的单跨输电导线气弹模型，其外径为42.08 mm，线密度3 100 kg/m，弹性模量60.6 GPa，跨度500 m，弧垂17.5 m，分裂间距500 mm。气弹模型设计时，除应该满足几何相似以外，还应该满足质量相似、阻尼相似以及弗劳德数、斯托罗哈数、柯西数等气动参数的相似，虽然在风洞中难以满足雷诺数相似的要求，但是由于多分裂输电导线间气流的相互穿梭扰乱了漩涡的形成，使得雷诺数效应并不显著，本文模型设计时不予考虑，气弹模型相似参数如表1所示。

表1 输电导线气弹模型相似参数

基于此，采用铜丝模拟输电导线的拉伸刚度，采用塑料管模拟输电导线的外形，分段包于铜丝之外，不提供输电导线模型的拉伸刚度，并用铅丝紧密缠绕于塑料管表面提供附加质量以模拟输电导线的线密度，且对输电导线的迎风面积影响甚微。使用1 mm厚ABS板模拟六分裂输电导线间隔棒，其质量相对于输电导线本身而言可以忽略，间隔棒的设计如图1所示。

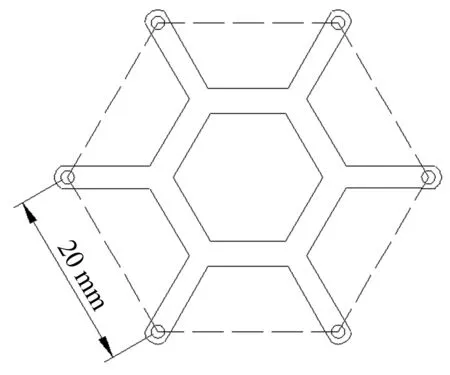
图1 间隔棒模型设计Fig.1 Spacers design

1.2 风洞试验

输电导线气弹模型风洞试验(如图2所示)在西南交通大学XNJD-3号风洞中进行，该风洞为立式回流闭口式边界层风洞，试验段截面宽22.5 m，高4.5 m，长36 m。试验风速范围为1～16.5 m/s连续可调。试验时，采用多个尖劈和分布立方体粗糙元模拟输电塔-线体系B类典型地貌紊流风场。图3(a)、3(b)为模型放置位置的平均风速和紊流度剖面、脉动风速功率谱密度与Karman谱的对比。

图2 气弹模型风洞试验Fig.2 Aero-elastic model wind tunnel test

采用六分量测力天平测试输电导线端部动张力, 测力天平采样频率均为200 Hz，采样时间90 s。风向角90°～0°，间隔10°的一个工况，本文针对最不利风向角90°时的情况进行研究。风洞试验风速2～7 m/s，间隔0.5 m/s。风向角及坐标定义如图4所示，测力天平的三个剪力测试分量分别对应于输电导线水平向、竖向以及顺线向端部张力分量。

图3 风场模拟Fig.3 Wind field simulation

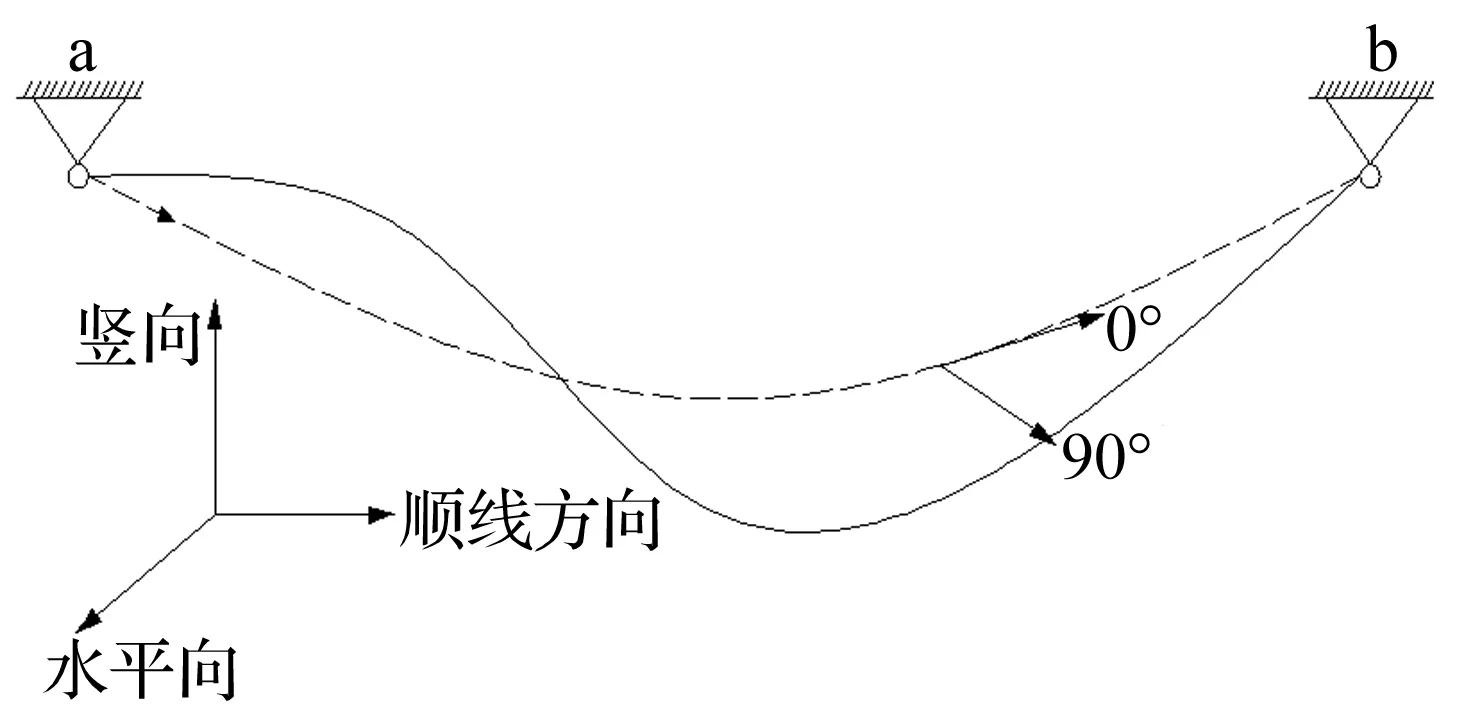
图4 风向角及坐标定义示意图Fig.4 Definition of wind direction and coordinate

2 动力特性测试

根据悬索理论[10]，可以求得本次试验输电导线模型振型频率的理论解， 为了验证输电导线气弹模型制作的效果，对输电导线模型进行了自由振动响应的测试，采用测力天平测得张力进行频率的识别。图5和图6给出了输电导线自由振动平面内、平面外动张力时程以及对应的功率谱密度函数，并可以识别出结构的前四阶振型阻尼比及频率，识别结果与理论值对比如表2所示。由表2可以看出输电导线模型面外一阶对称振型频率实测值为0.66与目标值比较接近，竖向激发出面内一阶对称振型，其频率为1.63与目标值也比较接近，同时也激发出了具有一定贡献的二阶振型，且频率与理论值也比较接近，从而验证了本文模型制作的可靠性。

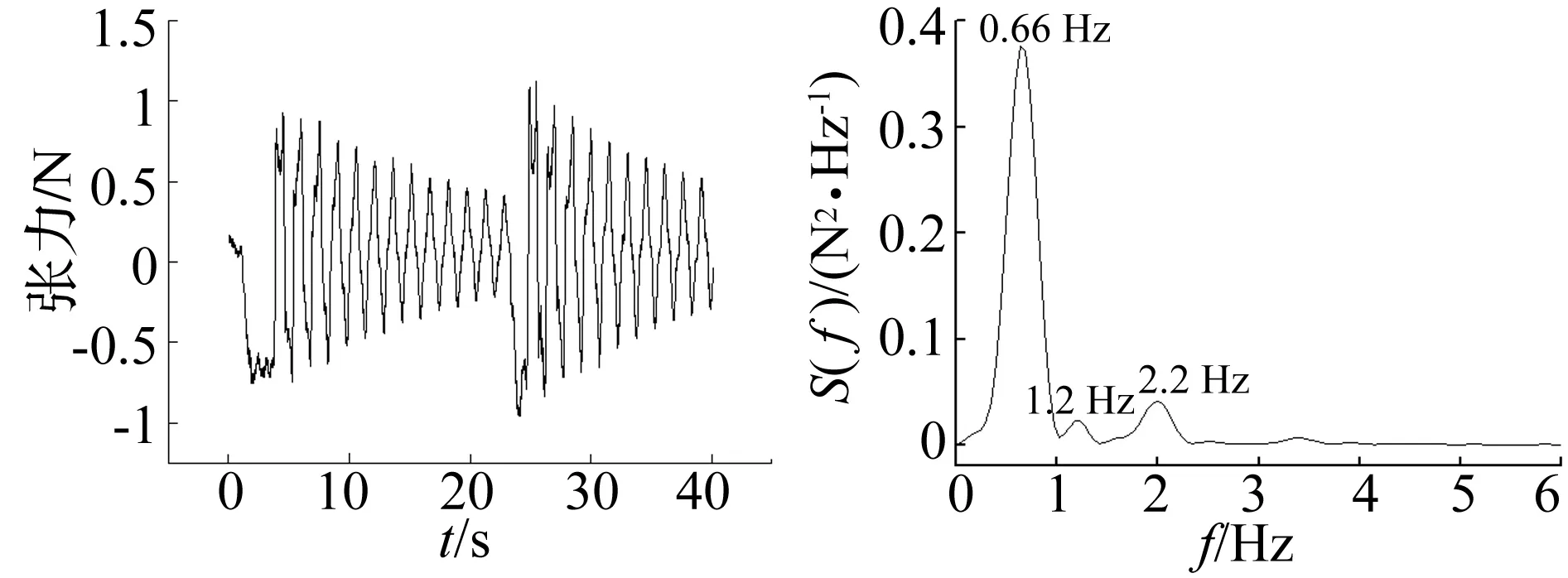
图5 输电导线平面外自由振动及功率谱Fig.5 Time history and PSD of out-of-plane tension of transmission conductor

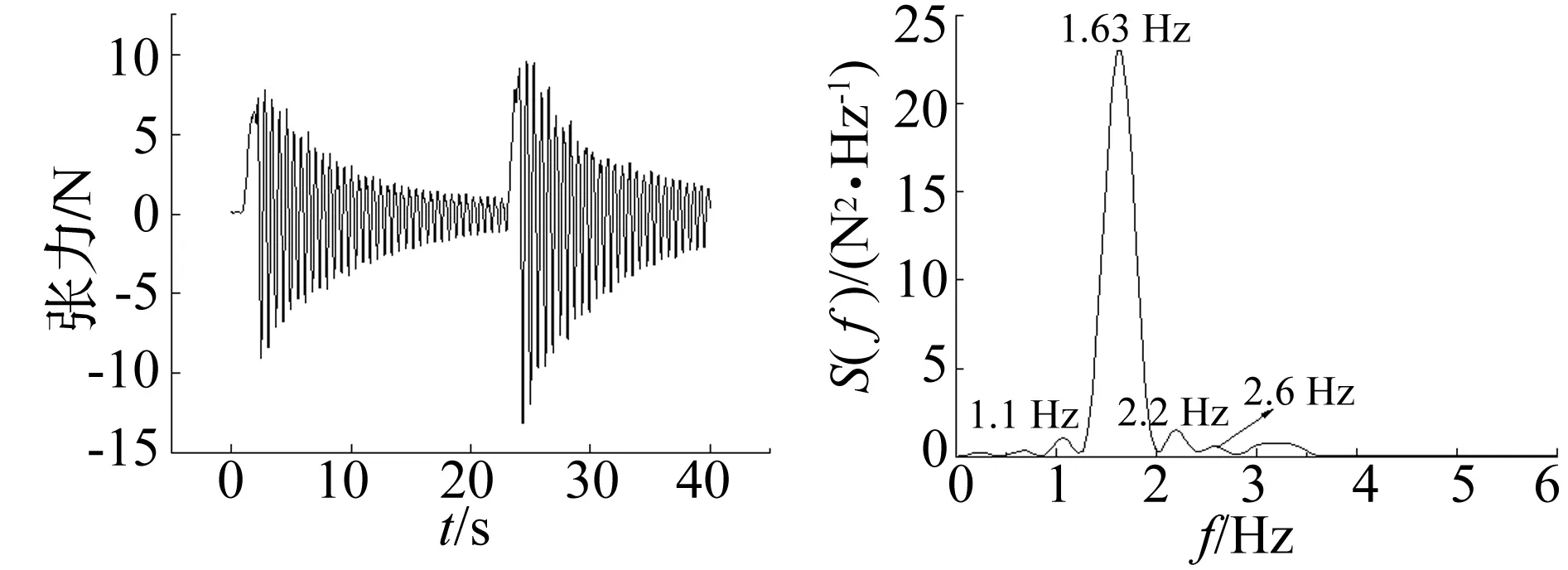
图6 输电导线平面内自由振动及功率谱Fig.6 Time history and PSD of in-plane tension of transmission conductor

阶数理论频率/Hz实测频率/Hz阻尼比/%振型描述10.650.660.97面外对称振型21.31.21.11面外反对称振型31.61.631.54面内对称振型42.152.21.64面内对称振型

3 气动阻尼识别与分析

3.1 气动阻尼识别

由于输电导线的风致振动频率分布特别密集，其动张力数据包含很多频率十分接近的成分，如图7所示，为90°风向角时，输电导线端部动张力功率谱。单纯的使用随机减量技术(RDT)进行气动阻尼识别，得到的自由振动信号往往会产生频率混叠的现象，这样会影响阻尼识别的精度。为此，本文根据文献[7]提出的EMD,小波分析以及RDT相结合的方法，对输电导线的气动阻尼进行识别。

通过EMD分解得到各个IMF分量，进而挑选出与输电导线各阶振型频率对应的IMF量。图8给出了试验风速7 m/s时，输电导线水平向动张力通过EMD分解得到的前5个IMF分量及其频谱。从图8可以看出,前3个IMF分量分别为高频的噪声以及结构的高频分量，第4个和第5个IMF分量分别对应于输电导线的面内一阶和面内二阶对称振型信号，频率为2.2 Hz及1.6 Hz，而第6个和第7个IMF分量对应于输电导线的面外一阶、二阶振型，频率分别为0.66 Hz及1.2 Hz，但限于篇幅，本文没有给出相应的时程及频谱图。

图7 输电导线动张力功率谱Fig.7 Power spectra of dynamic tensions

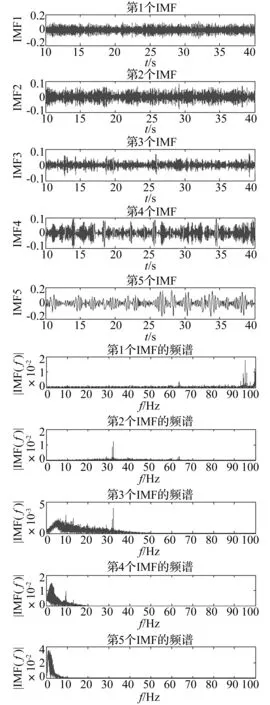
图8 IMF分量及其频谱Fig.8 IMF component and its spectrum

从图8还可以看出，尽管EMD能够得到频率成分相对单一的时程信号，但是依然存在部分频率非常接近的成分混叠的现象，文献[11]指出对信号进行连续的复Morlet小波变换可以方便地解决这个问题，限于篇幅，具体方法本文不再赘述。因此,进一步通过小波变换，对其进行处理，便可以得到更为纯净的信号，最后通过RDT进行气动阻尼识别，从而使得识别结果更为精确。图9给出了根据上述方法得到的输电导线前两阶振型自由衰减曲线，可以看出得到的自由衰减曲线比较平滑，气动阻尼识别结果比较稳定。

图9 随机减量衰减曲线Fig.9 RDT decay curve

3.2 基于准定常理论的气动阻尼计算

对于来流垂直作用于输电导线轴线方向的情况，其运动与作用力如图10所示。

图10 输电线风致振动示意图Fig.10 Incident wind and resulting force on a moving transmission line

基于准定常理论，输电导线单位长度上的阻力可表示为[12]：

(1)

式中，ρ为空气密度，D为输电线直径，CD为阻力系数，u为输电导线的运动速度，V为来流风速，φ为来流风速与输电导线运动方向的夹角。

忽略高阶小量，式(1)可近似为：

(2)

式(2)表明阻力包含作用于输电导线上的拟静力项和与输电导线运动速度成正比的气动阻尼力项，因此气动阻尼可表示为：

(3)

式中，ωn为输电线的第n阶圆频率，m为输电导线的线密度。

需要指出的是，既有研究[13]表明输电导线阻力系数并不是取规范规定的一个值，而是随风速的变化而变化，因此为了符合实际，在计算气动阻尼比时，阻力系数取试验的实测值。φ的取值由输电导线平均风偏角确定：

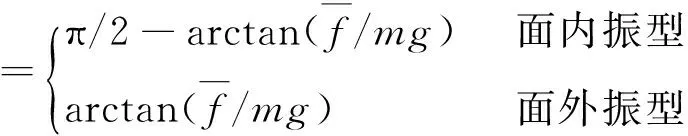
(4)

3.3 气动阻尼分析

图11和图12分别给出了输电导线各阶振型气动阻尼识别结果以及基于准定常理论计算得到的各阶振型气动阻尼。从图11可以看出：① 总体而言，输电导线各阶气动阻尼比都大于零，且均随风速增加而呈递增趋势，强风作用下，输电导线的振型气动阻尼比可达结构振型阻尼比的十倍以上，气动阻尼比相对于结构阻尼比占绝对的主导地位；② 输电导线低阶振型气动阻尼比相对于高阶振型气动阻尼比大。对比图11与图12可知：基于准定常理论计算得到的气动阻尼比相对于识别结果随风速的变化规律基本一致，但基于准定常理论计算得到的输电导线面外振型气动阻尼比大了近一倍之多。而面内振型气动阻尼比相对于识别结果小得多，且随风速变化不大。这种差异产生的原因是：由于基于准定常理论计算的气动阻尼比只考虑了单根输电导线的情况，不能考虑多分裂输电导线几何尺寸的影响，多分裂输电导线迎风面积并不是单根线的简单倍数，分裂输电导线间的相互干扰同样会引起气动阻尼的变化，且准定常假定包含了结构运动应大大小于风速(需要考证，就是假定的条件)，而导线为大变形，多模态参与，因此准稳定理论的结果是否适用于输电导线顺风向风致振动值得商榷。

图11 输电导线各阶振型气动阻尼比识别结果Fig.11 Identification results of aerodynamic damping ratio of transmission conductor for different modes

图12 输电导线各阶振型气动阻尼比计算结果Fig.12 Calculation results of aerodynamic damping ratio of transmission conductor for different modes

4 动张力计算

为了分析气动阻尼对输电导线风致动张力的影响，本文基于文献[14-15]提出的大跨越输电线路风振动张力模型，计算得到了考虑气动阻尼与不考虑气动阻尼情况下输电导线动张力。

4.1 输电导线动张力模型

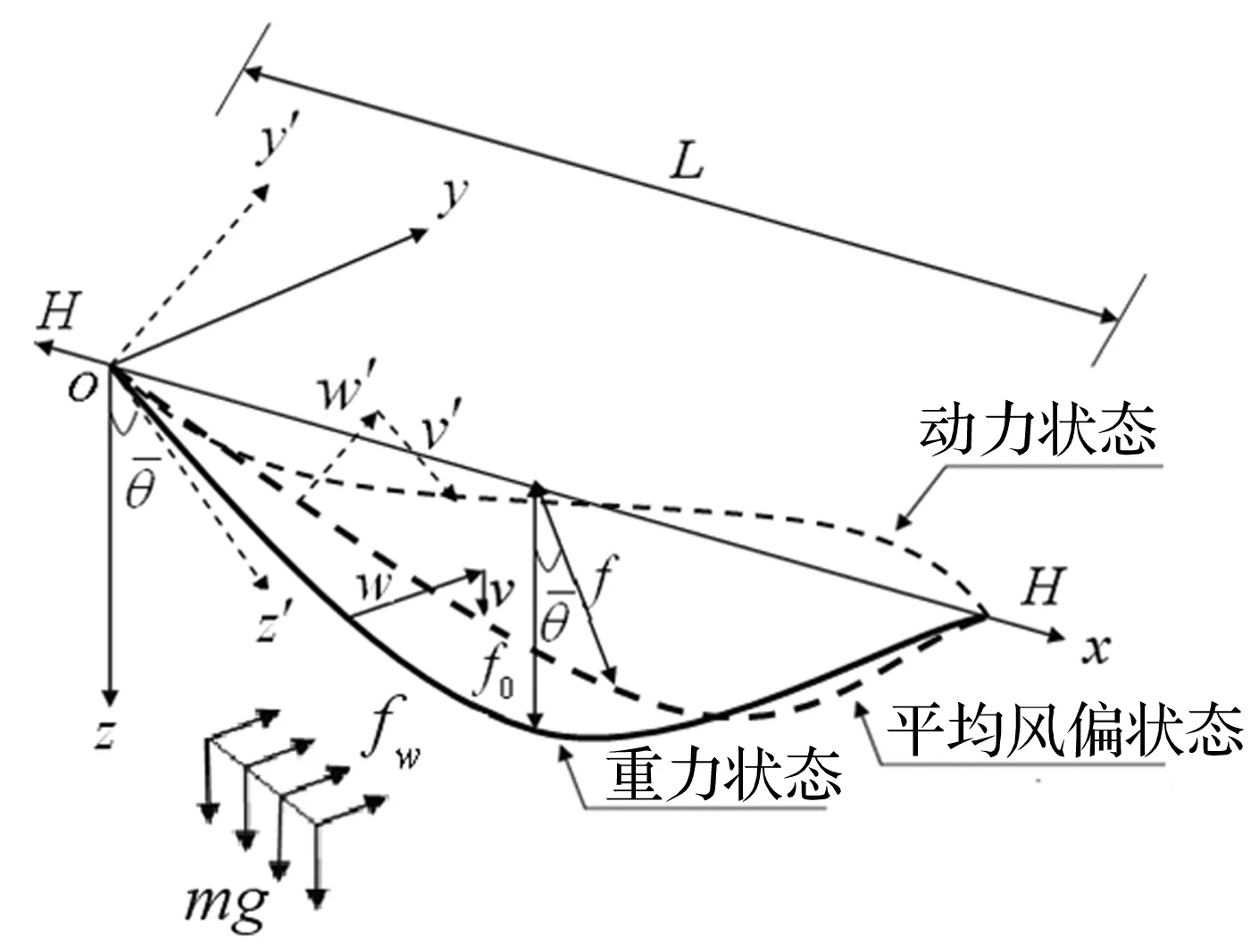
图13 输电导线空间动态构形(文献[14])Fig.13 Space dynamic configuration of conductor

在脉动风作用下，以输电导线平均风偏状态时的形状和刚度为条件计算脉动风作用时输电导线的频率与振型，再运用振型叠加法求解脉动位移和相应的顺线向动张力，进而根据矢量平衡条件就可以得到支座动张力的3个方向的分量。输电导线三个方向动张力的理论功率谱可以表示为：

(5)

(6)

(7)

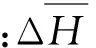
(8)

(9)

(10)

(11)

式中:*表示复数的共轭。

大多数情况下，对于张紧的小垂跨比输电导线，其竖向尺寸与水平向尺寸相比要小得多，所以，式(8)～式(10)只考虑了风荷载在水平方向上的空间相关性，而忽略了竖向的相关性。与我国目前荷载规范一致，水平相关性采用Shiotani简化相关函数，表示为

(12)

式中，Su(ω)是风速功率谱，可以采用风洞模拟的卡门谱。由于广义位移互谱之间存在以下关系：

Sv′w′*(ω)=Sw′v′(ω)

(13)

所以式(1)～式(3)可以进一步整理为：

(14)

(15)

(16)式中:real表示复数的实部。其他参数意义与上述参数相同。

4.2 计算结果及分析

根据动张力模型可以计算得到输电导线各个方向的动张力，如图14所示。从图可以看出：① 对水平向和顺线向而言，不考气动阻尼会高估输电导线的动张力，尤其在强风作用下，动张力将被严重高估；② 对竖向而言，在较低风速下，考虑与不考虑气动阻尼对输电导线动张力的影响不大，强风作用下，不考虑气动阻尼亦会高估其动力响应；③ 考虑气动阻尼的动张力计算结果与试验实测结果吻合的比较好，说明了在进行输电导线风致动张力计算时，其气弹效应不可忽略，同时也验证了输电导线动张力理论模型的可靠性。

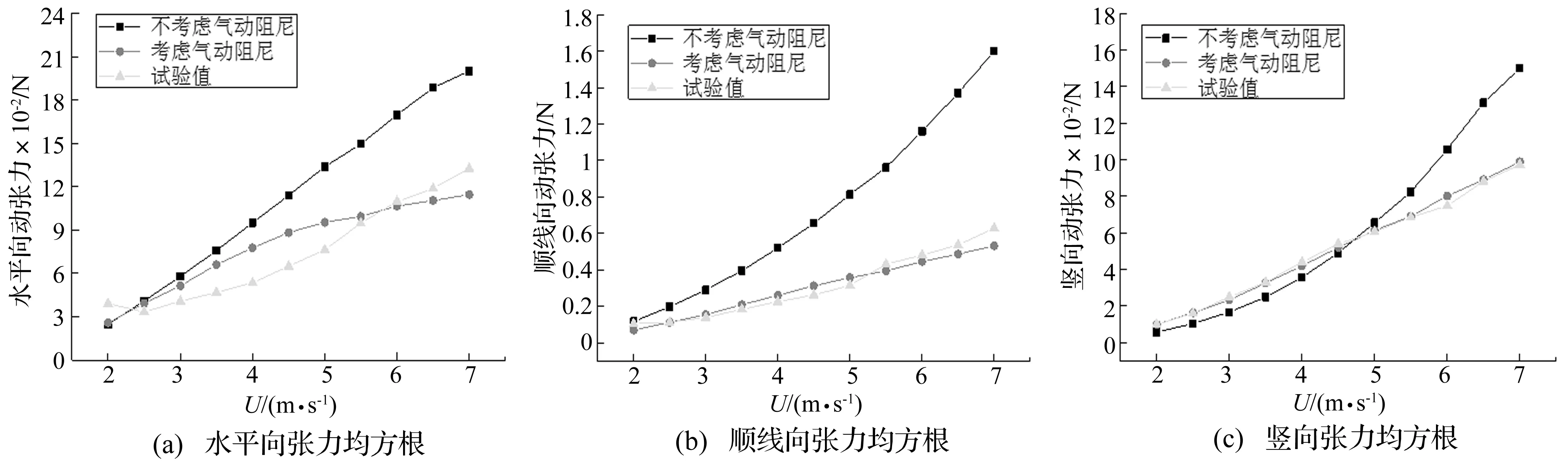
图14 输电导线端部张力均方根值比较Fig.14 Compare of RMS tension at the end of the transmission conductor between calculation and test

5 结 论

本文结合使用EMD，小波分析及随机减量技术识别了输电导线前四阶振型气动阻尼比，并根据动张力模型计算得到了考虑与不考虑气动阻尼对输电导线风致动张力的影响，得到主要结论如下：

(1) 输电导线振动能量表现为密频分布特性，综合使用EMD，小波分析及随机减量技术可以更好消除频率混叠，得到更纯净的自由振动衰减曲线，从而使得识别结果更为精确、稳定。

(2) 输电导线各阶振型气动阻尼比均为正值，且随风速增加而递增，强风作用下输电线的振型气动阻尼比可达结构振型阻尼比的十倍以上，气动阻尼比相对于结构阻尼比占主导地位。

(3) 输电导线低阶振型气动阻尼比相对于高阶振型气动阻尼比大。

(4) 基于准定常理论计算得到的气动阻尼比相对于识别结果大将近一倍，且由于面内外耦合非线性的振动特性，使得基于准定常理论计算得到各阶振型气动阻尼比之间的差异更为显著，基于准定常理论的计算结果值得商榷。

(5) 输电导线气动阻尼比对其风致响应计算的影响较大，强风作用下，不考虑气动阻尼会严重高估输电导线的风致响应。

[1] DAVENPORT A G. The response of tension structure to turbulence wind: the role of aerodynamic damping [C]// Proceeding of First International Oleg Kerensky Memorial Conference on Tension Structures. London: American Society of Civil Engineers, 1988: 20-22.

[2] MOMOMURA Y, MARUKUWA H, OKAMURA T, et al. Full-scale measurements of wind-induced vibration of a transmission line system in a mountainous area [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 72: 241-252.

[3] MAEDA J, MORIMOTO Y, ISHIDA N, et al. Aerodynamic damping properties of a high-voltage transmission tower [C]// Proceeding of 5th International Symposium on Cable Dynamic. Santa Margherita Ligure, Italy,2003.

[4] FUJIMURA M, MAEDA J, MORIMOTO Y, et al. Aerodynamic damping properties of transmission tower estimated using a new identification method [C]// Proceeding of the 12th International Conference on Wind Engineering. Cairns, Australia, 2007.

[5] TAKEUCHI M, MAEDA J, ISHIDA N. Aerodynamic damping properties of two transmission towers estimated by combining several identification methods [J]. Journal of Wind Engineering and Industrial Aerodynamics,2010,98(12): 872-880.

[6] 任坤，李正良，肖正直，等．环境激励下特高压输电塔线体系气动阻尼的识别[J]．重庆工学院学报(自然科学)，2009，23(7): 64-68.

REN Kun, LI Zhengliang, XIAO Zhengzhi, et al. Aerodynamic damping identification of UHV transmission line system under ambient excitation [J]. Journal of Chongqing Institute of Technology (Natural Science), 2009，23(7):64-68.[7] 邹良浩，梁枢果，王述良. 基于气弹模型风洞试验的输电塔气动阻尼研究[J]. 振动、测试与诊断，2015，35(2): 268-274.

ZOU Lianghao, LIANG Shuguo, WANG Shuliang. Analysis of aero-dynamic damping of transmission tower based on aero-elastic model wind tunnel [J]. Journal of Vibration, Measurement and Diagnosis, 2015，35(2): 268-274.

[8] 段成荫，邓洪洲. 基于特征系统实现算法的输电塔气动阻尼风洞试验研究[J]. 振动与冲击，2014，33(21):131-136.

DUAN Chengyin, DENG Hongzhou. Wind tunnel tests for aerodynamic damping of a transmission tower based on eigensystem realization algorithm [J]. Journal of Vibration and Shock, 2014, 33(21): 131-136.

[9] 楼文娟，杨悦，吕中宾,等. 考虑气动阻尼效应的输电线路风偏动态分析方法[J]. 振动与冲击，2015，34(6):24-29.

LOU Wenjuan, YANG Yue, LÜ Zhongbin, et al. Windage yaw dynamic analysis methods for transmission lines considering aerodynamic damping effect [J]. Journal of Vibration and Shock, 2015, 34(6):24-29.

[10] IRVINE H M. Cable structure [M]. Cambridge, MA: The MIT Press,1981.

[11] 吴海洋,梁枢果,邹良浩. 基于小波分析的高层建筑气动阻尼评估方法[J].振动与冲击，2008, 27(8): 93-96.

WU Haiyang, LIANG Shuguo, ZOU Lianghao. Method of evaluating aerodynamic damping of tall buildings based on wavelet analysis [J]. Journal of Vibration and Shock, 2008, 27(8): 93-96.

[12] MACDONALD J H G. Separation of the contributions of aerodynamic and structural damping in vibrations of inclined cables [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002,90(1): 19-39.

[13] 谢强,孙启刚,管政. 多分裂输电线整体阻力系数风洞试验研究[J].电网技术，2013,37(4):1106-1112.

XIE Qiang, SUN Qigang, GUAN Zheng. Wind tunnel test on global drag coefficients of multi-bundled conductors [J]. Power System Technology, 2013,37(4):1106-1112.

[14] 汪大海，李杰，谢强. 大跨越输电线路风振动张力模型[J]. 中国电机工程学报，2009，29 (28): 122-128.

WANG Dahai, LI Jie, XIE Qiang. Dynamic tension model for wind-induced vibration of long spanned transmission line [J]. Proceedings of the CSEE, 2009, 29 (28): 122-128.

[15] WANG Dahai, LI Jie, XIE Qiang. Analytical model for dynamic tension in overhead power transmission lines subject to strong wind[J]. Advances in Structural Engineering, 2011, 14(3): 445-456.

Aerodynamic damping effects of a transmission conductor by wind tunnel tests

WANG Shuliang1, LIANG Shuguo1, ZOU Lianghao1, WANG Dahai2

(1. School of Civil Engineering, Wuhan University, Wuhan 430072, China;2. School of Civil & Architecture, Wuhan University of Technology, Wuhan 430070, China)

Based on aero-elastic model wind tunnel tests of a single-span six-bundled transmission conductor, time series of dynamic tensions at the end of the conductor under various wind speeds, namely the force transmitted to the tower, were measured by the force balances. Through the dynamic tensions, the first four modal aerodynamic damping ratios were evaluated by combining the empirical mode decomposition (EMD) method, wavelet analysis, and random decrement technology (RDT). The results were compared with those obtained by quasi-steady theory. Then, considering the effects of aerodynamic damping, wind-induced responses were calculated. The results illustrate that aerodynamic damping is dominant relative to the structural damping, which may reach more than ten times of structural damping ratio; due to the wind-induced nonlinear vibration of the conductor, the discrepancy of aerodynamic damping ratio obtained by wind tunnel tests and quasi-steady theory is significant; wind-induced dynamic tensions of the transmission conductor under strong wind would be overestimated seriously without considering the aerodynamic damping.

wind tunnel test; aero-elastic model; aerodynamic damping; transmission conductor; wind-induced response

国家自然科学基金项目(51078296)

2015-08-04 修改稿收到日期：2015-10-19

王述良 男，博士，1985年生

梁枢果 男，硕士，教授，1950年生

E-mail:liangsg@sohu.com

TH212；TH213.3

A

10.13465/j.cnki.jvs.2016.20.005