基于FLAC-3D黄土边坡地震作用下动力响应数值分析

桂永庆，袁宝远，邹　凯，王　强

（河海大学地球科学与工程学院，南京211100）

基于FLAC-3D黄土边坡地震作用下动力响应数值分析

桂永庆，袁宝远，邹凯，王强

（河海大学地球科学与工程学院，南京211100）

基于FLAC-3D有限差分软件建立一个典型的黄土边坡模型，分析地震动荷载作用下边坡的动力响应特性和动力失稳机制。边坡的水平位移图表明，地震作用下边坡坡脚位移向下，发生剪出变形，坡脚为薄弱部位；剪应变增量由坡脚逐渐向坡内、坡顶扩展，中部位置剪应变较静力作用下发生较大变化，塑性区从坡脚稍向上部位向坡体内部发展，范围增大；坡脚、坡面、坡顶和坡内等监测点的速度时程曲线表明，地震波在坡体内传播过程中具有滞后效应，同时，坡体对地震波具有临空面放大效应。

黄土边坡模型；FLAC-3D；地震作用；动力响应；剪出变形；剪应变

0　引言

边坡是人类生活的重要环境，甚至是工程建筑的重要组成部分，随着我国经济的快速发展，工程建筑的步伐的加大，边坡工程的研究越来越多，水电，建筑等行业都存在大量的边坡问题，我国每年因为边坡导致的安全事故时有发生，给人们的生活带来了极大的不便，同时也对国家的经济建设带来了影响，使得我们不得不对边坡的稳定性进行详细的研究分析，我国黄土分布面积63.53万km2，占全国陆地总面积的6.63%［1］，大多处于地震区划的高烈度区，前人对边坡的稳定性研究，大多是在静力作用下进行的，对动力作用下的研究偏少，但实际情况中，有许多边坡会受到地震等动力作用的影响。目前，前人已经取得了一些边坡动力特性及地震动力响应的研究成果［2-4］，对地震作用下的黄土边坡动力响应研究较少［5-6］，所以对黄土边坡进行动荷载下的稳定性研究具有实际性意义。

本文主要的思路：先研究边坡在自身重力作用下的稳定性状况，研究其水平方向的位移，剪应变增量，坡脚、坡面、坡顶和坡内监测点的水平速度；然后位移场、速度场归零，在边坡模型底部引入一段自定义的地震波，再观测其水平位移场、监测点的剪应变增量等变化特征，分析动力响应规律。

1　数值模型的建立

1.1边坡算例

黄土是一种第四纪干旱、半干旱条件下沉积的陆相疏松堆积物，是一种广泛分布的特殊性土。在天然状态下，黄土的强度一般较高，压缩性较低。垂直节理发育，具有较强的结构性，颗粒组成以粉粒为主，具多孔性，颗粒间的胶结物质耐水性较差，在一定的压力作用或受水浸湿后，其结构会迅速破坏而发生显著附加沉降，导致建筑物破坏，此特性为黄土的湿陷性，人工开挖黄土边坡多高陡，这些特性决定了黄土研究的复杂性。本文以简单的黄土边坡概化模型为例，整个模型长100 m，高60 m，坡比1∶1，其平面示意图见图1。

图1　简单的一级边坡平面布置图Figure1　Simplified first grade slope situation plan

1.2网格模型

边坡计算范围为100 m×60 m×2 m，网格采用六面体单元和楔形体单元。边界条件：模型底部x、y、z三个方向位移约束，模型左右侧x方向位移约束，模型y方向位移约束。计算土体总单元数800个，土体单元节点1742个（图2）。

图2　FLAC-3D模型图Figure2　FLAC-3D model

1.3计算参数

材料采用理想弹塑性本构模型，Mohr-Coulomb屈服准则。土体的物理力学参数见表1。

表1　土体物理力学参数Table1　Parameters of soil strata

土体的体积模量K和剪切模量G与弹性模量E及泊松比μ之间的转换关系为：

由（1）式和（2）式计算得：体积模量K=82.5 MPa，剪切模量G=38 MPa。

2　考虑重力作用的边坡稳定性分析

首先分析该边坡在重力作用下的稳定性，主要方法是利用FLAC-3D自带的强度折减法进行稳定分析。强度折减技术［7］的要点是利用公式（1）和（2）调整土体的强度指标c，φ，其中Ft为折减系数，然后对土坡进行有限元分析，通过不断地增加折减系数Ft，反复分析土坡，直至其达到临界破坏，此时得到的折减系数即为安全系数Fs。上述公式为

强度折减法的优点是安全系数可以直接得出，不需要事先假设滑裂面的形式和位置，另外可以考虑土坡的渐进破坏过程。

再在土体内部的中心A（该点远离坡面）、坡脚B、坡顶C和坡脚到坡顶之间的中点D设置四个点，监测这四个点x方向上的速度变化情况以及最大不平衡力的变化状况。考虑重力作用下该边坡x方向上的位移情况，剪应变增量云图。计算的收敛准则为不平衡力比率（表示模型中平衡时节点的最大不平衡力和初始最大不平衡力的比值）按满足1×10-3的要求求解。

利用FLAC-3D自带的强度折减法solve fos命令，计算出边坡的安全系数值为3.02，该值远远大于1，说明该边坡的稳定性较好，满足安全要求。从图3可以看出，该边坡x方向位移在靠近坡脚处最大，约为5.9 cm（其中负值表示位移的方向与相应坐标轴的正方向相反，边坡土体向临空面方向移动）。位移呈圆弧状向内扩展，数值渐渐变小。说明自重对边坡的稳定性影响较小。

静力作用下边坡的剪应变增量最大值在坡脚处，为1.0469，应变范围主要集中在坡脚处，呈圆弧状，远离坡面的地方剪应变增量很小。因为该边坡的安全系数较高，虽然塑性区有从坡脚向坡顶发展的趋势，但未贯通，说明边坡的稳定性较好。

监测的四个点在静力作用下的x方向上的速度变化曲线如图5，观察可知，当坡体处于稳定状态时，各个监测点的速度时程曲线时段末的速度趋于0，坡体趋于稳定。

3　动力荷载作用下稳定性分析

图3　静力作用下边坡的x方向的位移云图Figure3　Slope X direction displacement nephogram under static effect

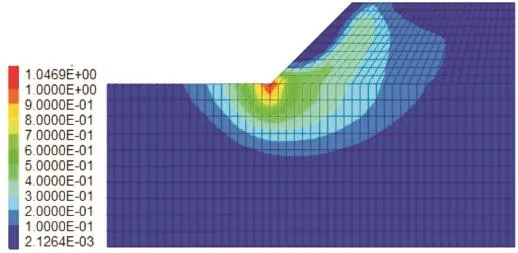
图4　静力作用下边坡的剪应变增量云图Figure4　Slope shear strain increment nephogram under static effect

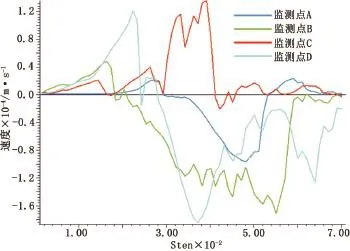
图5　静力作用下监测点x方向的速度时程曲线Figure5　Monitoring point X-axis velocities versus time curve under static function

对边坡进行动力作用下稳定性分析，首先消除自重作用形成的位移场和速度场，模型侧边界去除静力边界设为自由场边界，底部施加黏滞边界。地震是动力荷载常见形式之一，对建筑物的危害较大，为模拟地震作用下边坡的动力响应特性，FLAC-3D中地震动荷载的输入采用加速度时程、速度时程、应力时程和力时程四种方式设置局部阻尼，阻尼系数为0.314，FLAC-3D程序可以输入的动力荷载的形式有FISH函数，table命令定义的表，设置局部阻尼，阻尼系数为0.314，本文采用FLAC-3D的内置FISH语言编程，输入一段关于速度的人工合成地震动时程的方程，以此对边坡进行动荷载稳定性分析，输入的速度时间持续3 s，如图7所示，输入波在0.3～2.0 s时间段速度达到最大值。2.0～3.0 s速度逐渐变小趋于零。

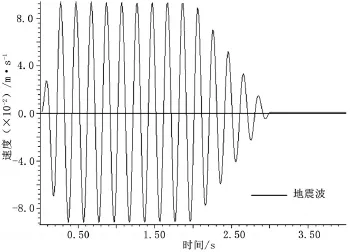
图6　输入波的速度—时间曲线Figure6　Incoming wave velocity-time curve

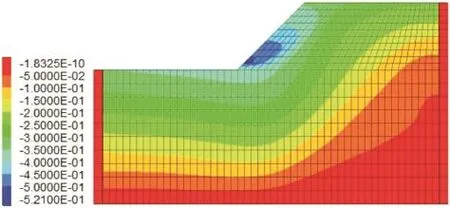
图7　动力作用下边坡的x方向的位移云图Figure7　Slope X direction displacement nephogram under dynamic effect

图8　动力作用下边坡的剪应变增量云图Figure8　Slope shear strain increment nephogram under dynamic effect

动力作用下位移的变化范围明显增大了，水平方向上的位移产生较大的变化，最大值为52 cm，在坡脚处，表明坡脚处由于受到上部滑坡体的挤压，而出现鼓胀现象；从坡脚到坡顶位移量呈圆弧型渐渐变小，坡顶处的位移为20 cm，坡顶在竖直方向下运动，而使坡度出现拉伸裂纹。从数值上可知坡体在水平方向，向坡外滑动。

剪应变增量由坡脚逐渐向坡内，坡顶扩展，中部位置剪应变较静力作用下发生较大变化，剪应变增量最大值在坡脚稍向上部位，为4.15×10-2。图9中明显看到贯通区，即潜在滑动面，说明这一区域已经处在不稳定的状态，随时间的推移，将会出现明显滑动。通过软件自带的强度折减法计算出安全系数为0.96。在实际工程当中，一般认为安全系数在1.2以上的边坡为安全稳定的。因此对此类边坡可以根据实际情况采取治理措施。

地震波在边坡中传播时，土体介质、结构、坡面、自由面的存在会改变地震波的传播路径、频谱及振幅值，导致坡脚、坡面、坡顶的响应发生变化［8］。监测的四个点在动力作用下的x方向上的速度变化曲线如图10所示（1—代表坡内的一点，2—代表坡脚，3—代表坡顶，4—代表坡脚和坡顶之间的中点）观察可知，坡脚、坡顶和坡面三个监测点的变化在1s后曲线基本相同，最后都趋于零，不同的是监测点速度的最大值，。坡内的速度历时曲线与坡面的三个监测点变化曲线不同，主要原因是地震波在坡体内传播过程中具有滞后效应。2、3、4点的水平方向的峰值明显大于1点，说明边坡临空面对地震波具有放大效应。

图9　动力作用下监测点x方向的速度时程曲线Figure9　Monitoring point X direction velocity time-history curve under dynamic effect

对于类似本文的黄土边坡，为减少粉土边坡变形、失稳、破坏造成的损失，可以通过数值模拟手段来研究边坡的地震动力响应，从而研究黄土边坡在地震动力作用下的失稳规律，为黄土边坡的治理提供参考。

4　结语

（1）静力作用下，（边坡坡脚、坡顶、坡面和坡内各监测点的）边坡的水平方向的位移较小；地震动力作用下该边坡的水平位移明显增大，坡脚位移最大值为52 cm，由坡脚向坡内和坡顶扩展，坡体在水平方向坡外滑动。剪应变增量由坡脚逐渐向坡内，坡顶扩展，中部位置剪应变较静力作用下发生较大变化。

（2）地震波在坡体内传播过程中具有滞后效应。同时，坡体对地震波具有临空面放大效应。

（3）地震作用下边坡塑性区从坡脚部位向坡体内部发展，边坡坡脚位移向上，发生剪出变形或破坏，坡脚为薄弱部位，应加强防范支护。

［1］严西华.黄土高路堑边坡稳定性分析［D］.西安：长安大学，2001.

［2］刘怀忠，谢红强，何江达，等.基于FLAC～（3D）的边坡滑面搜索法及动力稳定性分析［J］.四川大学学报（工程科学版），2014，（S1）：111-115.

［3］言志信，郭斌，贺香，等.多级边坡平台宽度对边坡地震动力响应及破坏机制的影响［J］.岩土力学，2012，（S2）：352-358

［4］李海波，肖克强，刘亚群.地震荷载作用下顺层岩质边坡安全系数分析［J］.岩石力学与工学报，2007，（12）：2385-2394.

［5］何丽君，石玉成，杨惠林，等.地震作用下黄土边坡稳定性分析［J］.西北地震学报，2009，31（2）：142-147.

［6］言志信，曹小红，张刘平，等.地震作用下黄土边坡动力响应数值分析［J］.岩土力学，2011，（S2）：610-614.

［7］Dawson E M，Roth W H，Drescher A.Slope stability analysisby strength reduction［J］.Geotechnique，1999，49（6）：835～840.

［8］YAN Z X，CAI H C，WANG Q M，et al.Finite difference numerical simulation of guided wave propagation in the full grouted rock bolt［J］. Science China Technological Sciences，2011，54：1-8.

Loess Slope Dynamic Response Numerical Analysis under Earthquake Vibration Based on FLAC-3D

Gui Yongqing，Yuan Baoyuan，Zou Kai and Wang Qiang
（School of Earth Science and Engineering，Hohai University，Nanjing，Jiangsu 211100）

Based on finite difference software FLAC-3D has built a typical loess slope model to analyze slope dynamic response charac⁃teristics and dynamic failure mechanism.The slope horizontal displacement diagram has shown that under the earthquake vibration，displacement of slope toe is downward，shearing deformation happened，the toe is weak position.Shear strain increment expands gradu⁃ally form toe toward slope inside and top，in middle part changes greater than under static effect.Plastic range develops from toe slight⁃ly upward into slope inside，and range increased.Monitoring point velocity time-history curves of toe，surface，top and inside have shown that the earthquake wave propagation process inside slope has lag-effect，while slope mass on earthquake wave has free face magnified effect.

loess slope model；FLAC-3D；earthquake vibration；dynamic response；shearing deformation；shear strain

P642.27

A

10.3969/j.issn.1674-1803.2016.10.14

1674-1803（2016）10-0063-04

桂永庆（1992—），硕士研究生，主要研究方向为工程地质。

2016-06-12

责任编辑：孙常长