旋转机械长历程偏心故障的数值与图形特征获取方法研究

赵西伟，徐小力，，赵文祥，蒋章雷

(1.北京理工大学 机械与车辆学院，北京 100081；2.北京信息科技大学现代测控技术教育部重点实验室，北京 100192)



旋转机械长历程偏心故障的数值与图形特征获取方法研究

赵西伟1，徐小力1，2，赵文祥1，蒋章雷2

(1.北京理工大学 机械与车辆学院，北京 100081；2.北京信息科技大学现代测控技术教育部重点实验室，北京 100192)

研究采用采样点的波动稳定性描述偏心故障的程度，即通过对旋转机械长历程偏心故障数据采用信息融合、小波阈值降噪、数据压缩、构造特征方阵、计算特征值方差等方法获取故障的数值特征来描述偏心故障程度；利用小波分解获取低频时域信号和二维轴心轨迹方法探寻偏心故障劣化过程中在图形上的本质变化. 应用这三种方法获取转子实验平台模拟的长历程偏心故障的数值与图形特征，结果显示，所获取的数值和图形特征均随着故障的劣化而单向变化，因此，三种方法均能够有效表征偏心故障劣化的过程和程度，具有较高的稳定鲁棒性.

旋转机械；偏心故障；数值特征；图形特征；二维轴心轨迹

旋转机械的大量故障不是瞬时发生的，故障从开始、发展到恶化总有一段出现异常现象的时间，而且有征兆可寻. 观察和统计表明旋转设备的大部分故障是具有时间依存性的可预知的趋势性故障，采用科学有效的故障预测往往能够揭示故障的发展变化，有利于避免设备恶性事故和继发性事故的发生[1].

对于任何一种旋转机械故障类型来说，它的故障特征信息可分为两种：图形特征和数值特征. 对于故障图形特征的获取，在具体的工程实际应用中，往往关注的是一些由振动数据获得的参数图形，如时域、频域图、轴心轨迹图及其趋势图等. 近年来兴起的利用图形识别方法进行故障诊断的技术引起了人们的广泛兴趣，如利用振动三维谱图诊断发电设备中的各种常见故障[2-3]. 史东锋等[4]利用二维全息谱重构低频和倍频轴心轨迹的方法对旋转机械进行故障诊断；李智等[5]深入研究了图形处理技术在旋转机械振动故障诊断中的应用.

对于旋转机械故障的数值特征的获取，一般的做法是计算采样信号的故障敏感特征参数值，如用延迟时间、嵌入维数、关联维数、复杂度、最大李亚普诺夫指数、近似熵等参数值进行故障类型或故障程度的识别[6-10].

偏心故障是一种在旋转机械中常见的故障，对偏心故障的深入研究，准确获得故障图形特征和数值特征信息，继而对故障特征信息加以分析、诊断，并最终对偏心故障发展趋势进行预测，这对旋转设备的故障诊断与趋势预测具有重要意义.

1 偏心故障的数值特征获取方法探索

1.1 对于不同偏心故障程度时域信息的思考

假设某旋转设备上先后存在两种不同程度的偏心故障，并且两种故障状态下的转速与采样频率一致，通过信号采集仪采集这两个故障的振动数据.

如果旋转设备上只存在偏心故障而不存在任何其他故障，并且在数据采集的环境中也不存在任何干扰，单从对故障较为敏感的通道获得的时域波形图上来比较两个不同程度的偏心故障，相对于较轻微故障而言，较严重故障的时域波形必然会发生变化，并且这种变化不是瞬时或局部的，而是贯穿于整个采样时间段内的. 对于旋转机械来说，它的运动是周期性的，在实验中，转子每转一圈就是一个周期，这种周期特性又反映到了时域波形中，因此时域波形的周期与转子的旋转周期又是一致的.

综上分析，可以得出这样的结论：在理想条件下，对于每一种偏心故障程度的时域波形而言，下一个周期的波形应是前一个周期波形的复制. 进一步得出：不同偏心故障程度体现在时域波形上的变化可以通过一个或多个周期的变化来观察.

1.2 偏心故障数值特征获取方法探索

通常，偏心故障程度越严重，时域波形波动越剧烈，所以，在1.1中所述结论基础上，试想通过研究一个或多个旋转周期内采样点的波动稳定性来判断故障的程度，其具体方法如下.

由转速b(r/s)和采样频率fd(Hz)计算出每一个周期内的采样点数为

(1)

对式(1)约分，得到最简分数，即

(2)

式中：Tmin即为所能取的最小周期数；p为能取的最小采样点数，在截取数据时，所截取的周期数或采样点数必须为Tmin或p的整数倍.

假设信号采集仪的故障敏感通道个数为q，则可获得q列故障敏感数据，从这q列数据中的某一行开始算起截取p行，获得信号矩阵Wp×q，即

(3)

为了减小噪声对特征信息的影响，拟应用Matlab小波工具箱对矩阵W的列向量进行小波阈值去噪.

小波函数系选择db，系数选择10，同时分解层数选择2，这样可以在一定程度上抑制了噪声的影响，同时还基本完整地保留了原信号的特征信息. 将被降噪过的数据导出，构成新的信号矩阵Zp×q，

(4)

做常数矩阵Aa×p

(5)

取常数矩阵Bq×a

(6)

(7)

由方阵Z″的特征值λ1，λ2，…，λa构造特征向量：N=[λ1λ2… λa]，计算特征值λ的方差DN，

(8)

(9)

最后，对由不同数据分别计算得到的DN值进行归一化处理，处理后得到的数值即为所要获取的偏心故障特征数值. 归一化步骤为：① 对所获得的一组DN值进行从小到大排列；② 对DN值用科学计数法表达；③ 去数量级，对剩余部分数值保留到小数点后第4位.

需要注意的是，在算法中一旦确定了某一个参数，在以后的计算中就需持续使用，否则会产生错误结果.

1.3 相位差对计算结果的影响

当对下一组采样点进行计算时，假设在上一组计算中截取了3个周期的采样点(如图1所示实线之间“X”点)，那么在不连续数据(若数据连续则不会发生相位差影响)上截取下一组3个周期的采样点(如图1所示虚线之间“O”点)时会有相位差的影响，但这一影响不是由A、B两点之间的相位差造成的，由于在截取虚线部分之间的采样点时，A、B两点之间的采样点相当于被移到了C、D之间，这样不会改变计算结果对时域波形波动稳定性的定性描述(这也是连续数据不存在相位差影响的根本原因)，相位差的真实影响是由所截取的后一组采样点无法与前一组采样点在相位上重合，两者发生了交错(如图1所示X点和O点的交错)产生的，如无法对相位进行校准，那么只能通过设置较高的采样频率，缩小相邻采样点之间的间隔，使图1中的O点变成X点的近似点来尽可能减小因相位偏移带来的误差.

1.4 干扰因素对计算结果的影响

上述方法是建立在理想的偏心故障数据获取环境基础上的，但是在实际情况中，复杂的干扰因素是无法避免的，由此对1.2中计算结果产生的影响也是难以控制的，但是通过对计算方法和实际操作方法两方面的改进是可以最大限度避免干扰因素对诊断精度产生负面影响的.

一般情况下，干扰因素大体上可以分为3类：

① 持续干扰：这类干扰是贯穿于采样时间始终的，即只要采集仪在采集数据，这种干扰就无可避免的对数据产生影响，典型的有电磁干扰等.

② 长时间干扰：这类干扰并不是在采集仪采集数据时就一定发生，但是一旦发生，持续的时间通常是接近或大于采样时间的，比如风速、风向的连续变化引起的风机风轮转速持续变动等.

③ 瞬时干扰：这类干扰特点是干扰时间短暂，一般远小于采样时间，并且偶发性强，比如无意中对实验台的敲击等.

在实验室环境中常常会发生第①、③类干扰，为尽量降低干扰对计算结果产生的负面影响，在实际操作中要尽量使操作环境相对简单，减少意外情况出现的可能性，同时在计算上考虑在采样时间段内均匀、多次截取(一般考虑截取5～10次)数据，分别计算DN值，对于获得的每组DN值中明显偏大或偏小的数值，用“从众”的办法，将其视为受瞬时干扰影响值予以去除，其余的视为未被干扰影响值，并取平均值，作为这组数据最终的DN值.

1.5 故障区间-故障程度评价标准的建立

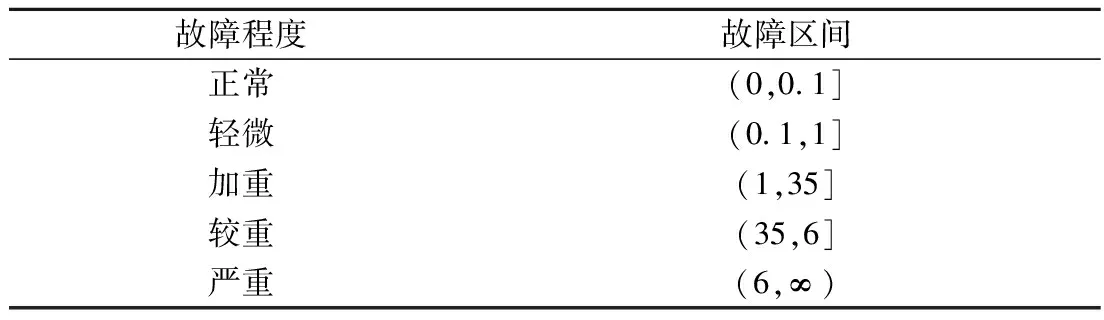
通过前面的分析可知：数据采集环境稳定、被检测对象转速不变的情况下所获得的DN值越大，意味着故障程度越严重，由此设想用不同的DN取值区间来描述不同的故障程度，例如(0，a1]表示无故障，(a1，a2]表示轻微故障，(a2，a3]表示中等故障，(a3，∞)表示严重故障(其中0

2 方法验证

2.1 实验验证

应用本特利转子实验平台验证前述方法的有效性. 由该实验平台获得了4组故障程度从无到有、逐渐劣化的偏心故障数据，其实验条件为：转速600 r/min，采样频率为10.24 kHz，每次采样时间为5 s，与采集卡1～4通道连接的传感器分别布置在了基座、轴向、水平径向、竖直径向上，那么故障敏感通道为3、4通道.

由式(2)确定截取的采样点数为1 024，令式(5)中的a=15，对这4组数据按照1.2节所述方法进行处理后获得表1.

表1DN值随故障程度劣化变化表

Tab.1DNchanges with the degree of deterioration of the fault table

故障程度数据维数l截取部位n1～n2DN值/105特征数值Q正常5120020000～21024003520122226247600352轻微5120020000～21024041133576755801904113加重5120020000～21024196573428420544219657较重5120020000～21024447508342557296744751严重5120020000～21024903080350043539990308

2.2 故障区间的建立

按照第1节中所述方法对大量的不同偏心故障程度的实验数据进行计算、分析发现，在每一种故障程度下获得的故障特征数值是有波动的，但基本上处于一个比较稳定的范围内，而且随着故障的劣化，波动范围也是单向变化的，那么可以判定故障程度与DN值波动范围具有一一对应关系，而在通常情况下，偏心故障的劣化又是一个连续的变化过程，那么故障特征数值也应该是连续变化的，因此，结合表1中的特征数值，可以构造一个连续变化的故障区间表，如表2所示.

表2 偏心故障区间表

当获得了新的故障特征数值之后，即可根据其所在故障区间判定被检测对象所处故障状态.

3 偏心故障的图形特征获取方法研究

3.1 轴心轨迹分析法

当转轴旋转时，它会绕转轴中心点振动，运动的轨迹就是轴心轨迹. 不同的故障类型或程度，其轴心轨迹也是不同的，因而轴心轨迹分析方法是一种较好的旋转机械故障类型和故障程度识别方法.

在转子转速分别为600 r/m和1 200 r/m条件下，对转子配重盘逐渐加配质量完全一致的螺钉0、2、4个，其轴心轨迹变化如图2～图3所示.

从理论上说，转子在转轴水平放置且无故障旋转的情况下，其轴心轨迹一般呈现为长短轴相差不大的椭圆，但是在不添加故障时所获得的图2(a)和图3(a)两幅轴心轨迹图，其形状略成曲线不光滑的环，原因在于实验中受噪声的影响，在转子无偏心情况下，特征信息较为微弱，受噪声影响较严重，致轴心轨迹曲线不够光滑. 而图2、图3中的第二幅轴心轨迹图与第一幅相比，显然在形状上前者更加接近第三幅轴心轨迹图，说明特征信息逐渐加强，噪声影响相对减弱. 图2(a)、2(b)图虽然存在故障从无到有的差别，但轨迹的光滑程度变化并不十分明显，表明噪声的影响依然较强烈. 如果再纵向比较图2(b)、图3(b)两图，两者故障程度相同，但轨迹曲线光滑程度差别较大，说明轴心轨迹曲线光滑与否并不是偏心故障有无的标志. 图2与图3之间存在的单环和双环以及线段的差别是由所分析的数据长短及部位影响造成的.

由位移传感器检测出来的轴心轨迹直接反映了轴心位置随时间的变化，而轴心位置变化的根本原因是外力作用的结果. 当转轴水平放置、转子旋转时，轴心受到重力和离心力作用，若转速恒定，偏心故障越严重，即配重螺钉质量越大时，离心力越大，变大的离心力拉动轴心向外扩张，致使图2、图3中出现了轴心轨迹范围逐渐扩大的结果.

而轴心轨迹之所以会呈现出一个椭圆的形状，是由轴心受到配重盘向下的重力作用造成的，换句话说，如果转轴是竖直放置，轴心轨迹所在平面是水平的，轴心所受配重盘重力方向沿转轴向下，那么随着偏心故障程度的劣化，轴心轨迹应该表现为半径逐渐变大的圆.

3.2 小波分析法

应用Matlab小波工具箱对一组长度均为2 048的4种偏心故障程度的振动数据进行二层db小波分解，截取低频a2部分对比，构成如下时域波形对比图.

已知图4中从上到下，偏心故障从无到有，程度逐渐加深. 通过仔细观察可以发现，4幅经小波阈值降噪的时域波形图中，随着故障程度的逐渐加深，幅值达到或超过4的波峰个数和幅值达到或低于-2的波谷个数有逐渐增加的趋势，但是图4中这一趋势不够明显. 一般情况下，采样点的波动稳定性变化趋势明显与否是由故障的绝对能量决定兼受采样传感器灵敏度和外界干扰的影响. 在采样传感器灵敏度和采样环境均固定的前提下，故障的绝对能量越大，采样点的波动势必会越剧烈，由实验平台模拟的偏心故障，其绝对能量(由螺钉质量、偏心距、转速共同决定)是有限的，因此，在实验环境相对纯净、噪声干扰有限的条件下，出现了随着偏心故障逐渐劣化，采样点波动稳定性单向变化趋势不够明显却仍然可辨的结果.

4 结 论

稳态下获得的逐渐劣化偏心故障的时域信号，其变化可以通过分次截取一个或几个周期然后对比来观察，此结论对于获取旋转机械稳态振动特征具有普遍意义.

在实验中应用1.2中所述算法获取偏心故障数值特征时，经过大量的运算表明，所获特征数值越大，则偏心故障程度越严重. 这一算法的思想基础为时域波形(或采样点)的波动稳定性是随故障程度的劣化而单向变化的，因而该方法在实际应用中具有一定的推广价值.

1.2与1.5节中所述算法的局限性主要有以下两点.

① 转速需恒定. 采样中转速变化越大该方法准确程度下降越明显.

② 被检测对象需固定. 每一个被检测对象最好都建立一套属于自己的评价标准，用一个被检测对象的评价标准去衡量另外一个同种类(或不同种类)设备的故障程度将会出现误差(或错误).

偏心故障的劣化体现在轴心轨迹上的本质变化是形状近似于圆或椭圆的轨迹的范围逐渐扩大，轨迹的具体形状由转轴竖直或水平放置决定.

偏心故障的劣化体现在小波分析低频信号图形上的本质变化为波形振动逐渐加剧，这也间接的证明了1.2中所述算法的思想基础是可靠的.

[1] 徐小力，王红军.大型旋转机械运行状态趋势预测[M].北京：科学出版社，2011.

Xu Xiaoli， Wang Hongjun. Large rotating machinery running trend forecasting[M]. Beijing: Science Press， 2011. (in Chinese)

[2] 褚福磊，李贵三，张正松.旋转机械常见故障的振动三维谱特征及其识别[J].清华大学学报，1996，36(7):86-91.

Chu Fulei， Li Guisan， Zhang Zhengsong. Vibration features in waterfall diagrams and identification of common faults in rotating machinery[J]. Journal of Tsinghua University， 1996，36(7):86-91. (in Chinese)

[3] 吴峰崎，孟光，荆建平.基于声信号三维谱分析的转子复合碰摩故障特征提取[J].振动与冲击，2005，24(6):79-140.

Wu Fengqi， Meng Guang， Jing Jianping. Feature extraction based on 3-D spectrum analysis of acoustic signal in rotor malfunctions[J]. Journal of Vibration and Shock， 2005，24(6):79-140. (in Chinese)

[4] 史东锋，屈梁生.轴心轨迹定量特征提取技术在回转机械诊断中的应用[J].化工机械，1999，26(1)：25-62.

Shi Dongfeng， Qu Liangsheng. Diagnostic analysis of rotating machinery using quantitative feature extraction of axis orbit[J]. Journal of Chemical Machinery， 1999，26(1)：25-62. (in Chinese)

[5] 李智，陈祥初，张振仁，等.图像处理方法在柴油机振动故障诊断中的应用[J].振动、测试与诊断，2002，22(4):300-324.

Li Zhi， Chen Xiangchu， Zhang Zhenren， et al. Application of image processing to diesel fault vibration diagnosis[J]. Journal of Vibration Measurement & Diagnosis， 2002，22(4):300-324. (in Chinese)

[6] 王炳成，任朝晖，闻邦椿.基于非线性多参数的旋转机械故障诊断方法[J].机械工程学报，2012，48(5):63-69.

Wang Bingcheng， Ren Zhaohui， Wen Bangchun. Fault diagnoses method of rotating machines based on nonlinearmulti-parameters[J]. Journal of Mechanical Engineering， 2012，48(5):63-69. (in Chinese)

[7] Fraster A M， Winney H. Independent coordinates forstrange attractors from mutual information[J]. Reviews of Modern Physics， 1993，33(2):1134-1140.

[8] Fraster A M. Information and entropy in strange attractors[J]. IEEE Transactions on Information Theory， 1989，35(2):245-262.

[9] Cao Liangyue. Practical method for determining the minimum embedding dimension of a scalar time series[J]. Physica D Nonlinear Phenomena， 1997，110(1):43-50.

[10] 王福来，达庆利.复杂性度量方法的改进及其在证券市场的应用[J].系统工程学报，2007，22(5):455-460.

Wang Fulai， Da Qingli. Improvement of complexitymeasure method and its application to the stock exchangemarket[J]. Journal of Systems Engineering， 2007，22(5):455-460. (in Chinese)

(责任编辑：孙竹凤)

Extraction Methods for Numerical and Graphical Features of Long Course Eccentric Fault of Rotating Machinery

ZHAO Xi-wei1，XU Xiao-li1，2，ZHAO Wen-xiang1，JIANG Zhang-lei2

(1.School of Mechanical Engineering， Beijing Institute of Technology， Beijing 100081， China; 2.Key Laboratory of Modern Measurement & Control Technology of Ministry of Education， Beijing Information Science and Technology University， Beijing 100192， China)

The eccentric fault is one of the typical faults of rotating machinery and it is important to accurately extract the numerical features and graphical features of eccentric fault in fault study. For this reason, some extraction methods were presented, including the fluctuation stability of sampling points was taken to describe the degree of eccentric fault; the information fusion, wavelet threshold de-noise, data compression, constructing features matrix, calculating the variance and so on were used to deal with the long course of eccentric faults data to describe the degree of eccentric fault; the low-frequency time-domain signal obtained by wavelet decomposition and two-dimensional axis trajectory were employed to explore the essence change in the fault deterioration process. The numerical features and graphical features of long course eccentric fault obtained with the three methods were simulated by a rotor experiment platform. Results show that the numerical features and graphical features change unidirectionally with fault deterioration. Therefore, the three methods can accurately track on the process and degree of eccentric fault, and all of them have a high stability robustness.

rotating machinery; eccentric fault； numerical features； graphical features； two-dimensional axis trajectory

2015-07-09

国家自然科学基金资助项目(51275052)；北京市自然科学基金资助项目(3131002)；北京市教育委员会科技计划面上项目(KM201411232020)；北京市教育委员会科研计划重点项目(KZ201311232036)

赵西伟(1985—)，男，博士生，E-mail:zhaoxiwei2010@163.com.

徐小力(1951—)，男，教授，博士生导师，E-mail:xuxiaoli@bistu.edu.cn.

TH 17

A

1001-0645(2016)09-0893-06

10.15918/j.tbit1001-0645.2016.09.003