基于圆形采样和稀疏表示模型的鲁棒目标跟踪

王保宪，唐林波，陈聪葱，赵保军，王水根，王洪友

(1.北京理工大学 信息与电子学院，北京 100081； 2.石家庄铁道大学大型结构健康诊断与控制研究所，河北，石家庄 050043； 3.白城兵器试验中心，吉林，白城 137001)



基于圆形采样和稀疏表示模型的鲁棒目标跟踪

王保宪1，2，唐林波1，陈聪葱1，赵保军1，王水根1，王洪友3

(1.北京理工大学 信息与电子学院，北京 100081； 2.石家庄铁道大学大型结构健康诊断与控制研究所，河北，石家庄 050043； 3.白城兵器试验中心，吉林，白城 137001)

为解决基于稀疏表示的跟踪算法在小样本空间中出现模板漂移而在大样本空间中实时性差的问题，提出了一种基于圆形采样的双重稀疏表示目标跟踪算法. 该算法对跟踪矩形窗数据进行圆形采样，这不仅保证了目标的灰度和结构信息，而且减少了背景信息干扰. 同时对稀疏表示得到的小模板系数引入距离权重判断函数，判断目标样本变化情况，提高模板更新效率. 最后引入HOG(histogram of oriented gradient)特征，对稀疏表示得到的多个次优解进行二次稀疏表示，有效解决小样本数量少带来的估计误差. 实验结果表明，该算法能够提高小样本空间中目标跟踪的鲁棒性和实时性.

稀疏表示；目标跟踪；模板漂移

目标跟踪是视频分析的热点问题，也是后续视频处理的关键. 近年来，目标跟踪技术应用到越来越多的视觉系统中，如车辆导航、视频监控等. 一种鲁棒的目标跟踪算法需要能很好地处理背景噪声、部分遮挡、光照变化以及目标运动不连续等问题. 文献[1]对当前目标跟踪的研究现状做了详细的分析. 其中，粒子滤波是一种基于贝叶斯估计理论的目标跟踪框架[2]. 该算法基于蒙特卡洛模型，通过利用粒子集来表示概率，可以用在任何形式的状态空间模型上.

近几年，信号稀疏表示[3]在目标跟踪[4-6]领域得到了很好的推广应用. 在粒子滤波框架下，这些方法认为目标样本可以近似由模板空间中的几个模板线性表示，从而将目标跟踪问题看作为一个在目标模板空间稀疏重构目标候选区域的L1范数优化问题(L1跟踪算法). 目标场景中出现的各种复杂变化，可以用小模板(单位矩阵)表示. 虽然L1跟踪算法取得了良好的实验效果，但是跟踪进程需要求解上百个L1优化问题. 粒子样本越多，需要求解的L1优化问题越多，算法的实时性就越差. 后续有学者对L1跟踪算法进行了一系列的优化，有效控制了算法的计算量[7]. 图1是文献[7]中的L1跟踪算法在实时性和粒子样本个数之间的对应关系图，不难看出算法的整体计算量仍与粒子样本个数成正相关关系. 然而基于粒子滤波框架的跟踪算法，往往需要通过产生来自目标分布的大量样本，才能很好地描述目标的非线性运动. 在小样本空间中，少量的粒子样本会带来目标估计误差. 跟踪误差不断累积，可能会出现模板漂移，最终导致跟踪失败. 针对上述问题，本文提出了一种基于圆形采样的双重稀疏表示目标跟踪算法. 旨在利用有限的粒子样本，实现目标在小样本空间的鲁棒跟踪.

1 基于圆形采样的表面模型

当前大部分目标跟踪算法主要采用矩形窗的方式获取图像目标信息. 这种获取跟踪目标信息的方式虽然简单有效，但是大部分跟踪目标的外观不一定符合矩形状，所以会引入一定程度的背景信息. 由背景信息干扰带来的误差会随着跟踪进程累积，在后续的跟踪进程中容易出现模板漂移，最后导致跟踪失败. 本文不再通过矩形窗的方式获取目标信息，而是通过对矩形窗的数据进行圆形采样. 一方面保证了目标的灰度和结构信息，另一方面减少背景信息干扰，大大提高了粒子样本对目标特征的描述能力.

1.1 圆形采样模型的建立

圆形采样是提取目标旋转不变特征的一种常用方式. 文献[8]提出了一种同心离散圆簇(CCDC)模型，并成功应用到了图形分类中. 本文将其改进并应用到任意矩形窗的数据采样中，从而可以极大地减少背景像素干扰，确保跟踪的稳定性. 为了使采样点均匀分布，增加一个约束条件：离散点间距与圆环间距相等，均用Δ表示. 对于每个圆环以0°位置为起始点，沿圆周方向每隔弧长建立一个采样点，由此得到图2所示的均匀圆形采样模型.

假设第1个圆环的半径为Δ，根据约束条件，第i个圆环上的离散点数为2πri/Δ. 这里·表示向下取整运算. 那么具有m环的均匀圆形采样模型总点数Nm为

(1)

由此可见，采样模型的离散点数只与圆环个数m有关，与间距Δ无关. 由于采样模型的总点数m直接决定了矩形窗粒子样本参与L1范数优化问题的数据维度，综合考虑文献[8]推荐的参数和目标跟踪的实时性，本文的m值取6，间距Δ值取25.

1.2 目标跟踪表面模型

在粒子滤波框架，常见的表面模型[9]有颜色直方图、Harr模型以及HOG模型等. 虽然这些模型以比较高的数据维度，描述了矩形窗的目标特性，但其应用到L1跟踪算法中会显著增加L1优化求解的复杂度. 本文的表面模型依然建立在像素域，但与文献[4，7]中不同的是本文根据目标跟踪矩形窗的比例情况，建立了一种自适应均匀圆形采样模型(adaptative uniform circle sampling，AUCS).

设跟踪矩形窗的尺寸为(r,c)，根据1.1节设定的参数值计算出均匀圆形采样的标准矩阵为Pd=(xd,yd)，则通过式(2)计算出对应矩形窗的圆形采样矩阵P=(x,y).

(2)

图3是自适应均匀圆形采样模型的示意图.

1.3 表面模型的稳定性分析

一个好的表面模型不仅需要对跟踪目标的内在变化具有自适应性，而且需要对跟踪场景出现的干扰具有鲁棒性. 本节主要分析AUCS表面模型的稳定性. 图4是原始跟踪目标的矩形窗图，图5是模拟跟踪目标背景出现了干扰. 图中的红色点代表AUCS模型的采样点.

本文利用余弦相似度对比背景干扰前后AUCS表面模型和原始像素模型[4,7]的稳定性. 余弦相似度量函数如下：

(3)

式中：A表示原始图像；B表示增加背景干扰后的图像. 表1为背景干扰后样本对比变化.

表1 背景干扰后样本对比变化

从对比结果看出在背景出现干扰时，AUCS模型受到的干扰小于原始像素模型[4，7]. 因此应用AUCS模型可以提高跟踪系统的稳定性.

2 目标跟踪中的模板更新

本文在AUCS表面模型基础上，对稀疏表示得到的小模板系数引入距离权重判断函数，判断目标样本发生的变化，有效控制模板进行更新，避免由此引起的模板漂移. 为了方便后续描述，这里先回顾下稀疏表示目标跟踪框架.

2.1 基于稀疏表示的目标跟踪

不同光照和视角下的目标外观，可以在一个低维子空间进行线性描述[4]. 在跟踪进程中，这些子空间由一些目标模板构成：T=[t1t2…tm]∈Rd×n(d≫n). 目标跟踪结果y∈Rd在模板空间T中的线性描述如下：

(4)

式中aT=[a1a2…an]T∈Rn代表了模板空间中每个模板的线性表达系数.

为描述背景噪声和可能发生的目标遮挡，将小模板矩阵I=[i1i2…… id]T∈Rd×d引入到式(4)中，即有

(5)

式中：aI=[e1e2… ed]T∈Rd是小模板的表达系数;A是由目标模板和小模板构成的字典;a是字典单元所有模板的表达系数.

由于目标在小模板空间上的表达是稀疏的，因而可通过求解式(6)中的L1优化问题估计出真实的目标样本.

(6)

(7)

这里c是个参数，用于调整高斯核函数.

2.2 模板更新准则

L1跟踪框架是通过判断小模板系数进行模板更新的，文献[4,7]中的算法对小模板系数处理比较简单，导致在出现背景变化或目标边界发生轻微遮挡时均会认为发生遮挡，并在后续几帧中不进行模板更新. 如果目标外观发生较大改变，但目标模板未及时更新的话，很容易导致后续跟踪失败. 对此，本文在AUCS模型(对背景像素不敏感)基础上，对小模板系数引入距离权重判断函数. 判断粒子样本的变化情况，提高模板更新的效率. 这里先探讨一下小模板系数与样本数据变化之间的对应关系. 假设目标模板仅有1个，即有t=[l1l2…ld]T∈Rd. 若目标样本y中有n个数据出现变化且都分布在样本前端，即有

现在将y代入到式(5)中，并展开如下：

对上式进行L1优化求解，得到稀疏表达系数a=[aTaI]T. 实验结果发现小模板系数aI中的非零值几乎全部分布在前n个系数中. 这与样本中数据发生变化的位置是相互对应的. 由此可得知，通过观察小模板系数中非零值的分布情况，可估计出目标样本中的哪些位置的数据出现变化. 图6～图8通过具体的实验，也证明了这一点.

实验对发生遮挡的lena图进行AUCS采样并记录发生遮挡的像素标号. 然后求解采样数据在原始图库上的稀疏表示系数. 对比实验数据，发现小模板中较大的系数值所在位置就是记录发生遮挡的像素标号.

在实际目标跟踪中，样本数据出现变化的原因主要有：背景出现噪声、部分遮挡、局部光照变化以及目标自身出现形变等. 其中背景噪声只会随机影响个别数据；局部光照变化和部分遮挡会影响样本的局部连续数据. 只有目标出现大片遮挡或形状骤变时，才会影响样本的大部分数据. 根据上述分析，为了去除背景随机噪声的干扰，需要剔除小模板系数中不连续的非零点. 同时考虑到采样数据的空间相关性，将小模板系数映射到圆环上并按照一种距离权重函数累加角度α到角度β上的系数值.

(8)

式中g(x)=c/r(x)为距离相关函数，其中r(x)是每个数据点所在的圆环半径，c是一个常量参数.f(x,θ)为每个采样点在角度θ上的小模板系数量化值.

(9)

这里v(x)是每个采样点对应的小模板系数值. 下面假设lena图受到4种不同程度的遮挡(图9)，分别计算4个角度方向([0 90°]、(90° 180°]、(180° 270°]和(270°，360°])上的遮挡置信度值，结果如图10.

实验发现，当遮挡物越靠近目标中心时，其遮挡置信度越高. 至此，本文在AUCS模型基础上，提出了一种新的控制模板更新准则. 该准则通过分析小模板系数，判断目标样本发生的变化并引入距离权重判断函数有效控制模板进行更新. 在这种判断准则下，跟踪算法对目标边界的轻微遮挡不敏感，鲁棒性更好. 图11是本文提出的模板更新准则.

3 二次稀疏表示

基于粒子滤波框架[2]的跟踪算法，需要通过产生大量关于目标分布的样本去描述目标的非线性运动. 在小样本空间中，由于粒子样本少导致目标跟踪的收敛性很差. 所以L1跟踪算法在小样本空间的最优解未必就是最好的目标状态估计值，相反存在的次优解值可能更贴近目标的真实状态. 图12和图13展示了文献[7]的跟踪算法在小样本(粒子样本为50个)空间中的部分跟踪结果.

从图12可以看到样本3的概率权重值小于样本50. 图13是对应样本的跟踪结果框图，其中红色框对应样本3，绿色框对应样本50. 很明显看出样本3更贴近目标真实状态.

为了避免跟踪算法在小样本空间中出现样本贫化现象，本文引入HOG特征[9]在稀疏表示存在次优解时，将次优样本和最优样本进行二次稀疏表示. HOG模型以较高的数据维度描述了矩形窗的目标特性，从而能在二次筛选中确定出更加贴近目标真实状态的样本. 由于参与二次稀疏表示的样本数很少，所以不会带来太大的计算量.

4 目标跟踪框架

经过上述分析和讨论，得出本文最终的目标跟踪框架，如图14.

5 实验结果与分析

本文跟踪算法在Matlab7.0平台上编写，算法选取的粒子样本个数均为50个. 所有代码在Intel B960(CPU2.2 GHz，内存2 GB)的笔记本电脑上运行. 实验采用了6组公开视频[11]来对比衡量算法的好坏. 这些视频包含了目标被遮挡、光照变化、运动抖动以及背景出现噪声等情况. 公平起见，与本文对比的跟踪算法代码均在作者提供的网站上获得，且所有跟踪算法在初始帧对跟踪目标的定位是相同的. 实验从定量和定性2个角度对比衡量APGL1算法[7]，MTTL1算法[10]和本文算法.

5.1 定量分析

本节将从两方面来对比衡量3种跟踪算法的性能：中心定位平均误差和每秒处理帧数.

表2描述了3种跟踪算法在6组视频上的中心定位平均误差. 实验表明本文跟踪算法在小样本空间上的跟踪精度好于APGL1算法[7]和MTTL1算法[10].

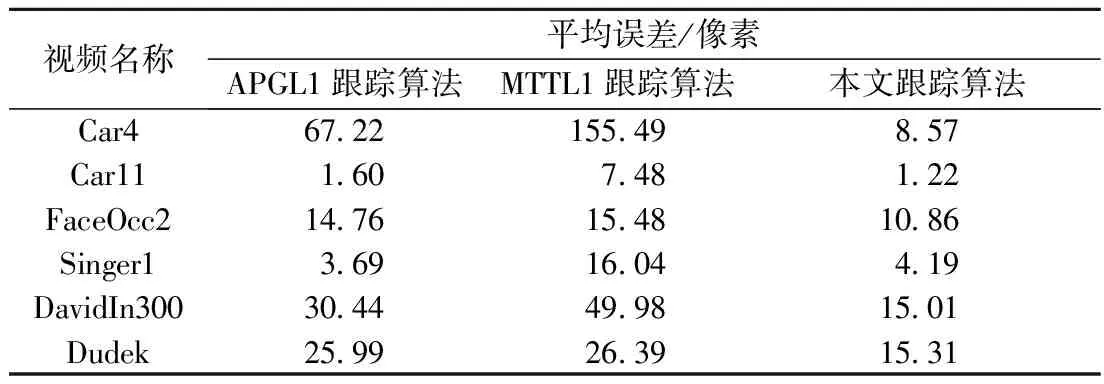
表2 3种跟踪算法的中心定位平均误差

由于本文采用了AUCS表面模型，所以每个样本的数据维度要少于原始像素模型的数据维度dorg. 而L1问题求解的复杂度与O(d)成正比关系，所以本文算法在处理效率应该高于另外两种算法. 从表3描述的3种算法的每秒处理帧数，也可看出本文算法的跟踪效率确实好于另外两种算法.

表3 3种跟踪算法的每秒处理帧数

5.2 定性分析

本节将从背景干扰、光照变化、目标被遮挡等方面定性分析3种跟踪算法的跟踪效果. 其中本文算法、APGL1算法和MTTL1算法的处理结果分别以红色框、绿色框和蓝色框进行展示.

5.2.1 背景干扰

图15和图16分别展示了Car11和DavidIn视频在出现背景信息干扰时，3种跟踪算法的处理结果. 在Car11视频中，当跟踪背景出现强干扰时，APGL1和MTTL1的跟踪窗均出现了漂移现象. 由于本文采用了AUCS表面模型，对背景信息产生的干扰不灵敏因而可以稳定地跟踪目标. 在DavidIn视频中，当跟踪目标附近出现类似干扰物时，由于本文采用了双重稀疏表示模型，在小样本空间中的估计误差明显低于另外2种跟踪算法，所以很好地抑制了模板漂移.

5.2.2 光照变化

图17和图18分别展示了3种跟踪算法在Car4和Singer1视频中出现光照变化时的跟踪效果. 从对比结果来看，本文算法的跟踪效果优于另外两种算法. 这与本文采用了二次稀疏表示机制有关. 在稀疏表示存在次优解时，本文引入了HOG模型重新描述粒子样本. 而HOG模型对目标的光照变化能保持很好的不变性，所以在小样本空间跟踪时本文算法的抗光照能力优于另外两种算法.

5.2.3 目标被遮挡

目标物被遮挡是引发模板漂移的一个重要原因，图19和图20分别展示了3种跟踪算法在处理Dudek视频中目标物出现不同程度遮挡时的跟踪效果. 相比于其他两种算法，由于本文通过分析小模板系数控制模板进行更新，因而可以较好地处理目标物发生遮挡. 其中在Dudek视频的211帧，本文算法能够有效地判断目标出现大范围遮挡，停止模板更新，避免引入手部遮挡部位. 在Dudek视频的365帧，在目标物出现小范围遮挡时其外观出现新的变化(摘掉眼镜)，本文算法能够及时地进行模板更新，避免后续跟踪发生漂移现象.

6 结 论

本文从表面模型建模出发，采用一种自适应均匀圆形采样模型，在不增加样本数据维度的前提下，提高了粒子样本对背景噪声的抗干扰能力. 同时在分析小模板系数结构的基础上，提出了一种新的模板更新准则，有效地控制目标模板更新. 最后，在稀疏表示存在次优样本时，引入HOG特征进行二次稀疏表示，大大提高跟踪算法在小样本空间上的稳定性. 实验数据分析表明，该算法在小样本空间跟踪时具有良好的鲁棒性和实时性.

[1] Yilmaz A， Javed O， Shah M. Object tracking: a survey[J]. Acm Computing Surveys， 2006，38(4):13.

[2] Isard M， Blake A. Condensation-conditional density propagation for visual tracking[J]. International Journal of Computer Vision， 1998，29(1):5-28.

[3] Donoho D. Compressed sensing[J]. IEEE Transactions on Information Theory， 2006，52(4):1289-1306.

[4] Mei X， Ling H， Wu Y， et al. Efficient minimum error bounded particle resampling L1 tracker with occlusion detection[J]. IEEE Transactions on Image Processing， 2013，22(7):2661-2675.

[5] Jia X， Lu H， Yang M. Visual tracking via adaptive structural local sparse appearance model[C]∥Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Providence: IEEE， 2012：1822-1829.

[6] Wang D， Lu H， Yang M. Online object tracking with sparse prototypes[J]. IEEE Transactions Image Processing， 2013，22(1):314-325.

[7] Bao C， Wu Y， Ling H， et al. Real time robust L1 tracker using accelerated proximal gradient approach[C]∥Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Providence: IEEE， 2012:1830-1837.

[8] 孙景乐，赵保军.用同心离散圆簇实现目标形状特征提取[J].系统工程与电子技术，2011，33(10):2317-2321.

Sun Jingle， Zhao Baojun. Shape feature extraction using a cluster of concentric discrete circles[J]. Systems Engineering and Electronics， 2011，33(10):2317-2321. (in Chinese)

[9] Li Xi， Hu W， Shen C， et al. A survey of appearance models in visual object tracking[J]. ACM Transactions on Intelligent Systems and Technology， 2013，4(4):58.

[10] Zhang T， Ghanem B， Liu S， et al. Robust visual tracking via multi-task sparse learning[C]∥Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Providence: IEEE， 2012:2042-2049.

[11] Wu Yi， Lim J， Yang M. Online object tracking: a benchmark[C]∥Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Portland: IEEE， 2013:2411-2418.

(责任编辑：刘芳)

Robust Object Tracking Based on Circle Sampling and Sparse Representation

WANG Bao-xian1，2，TANG Lin-bo1，CHEN Cong-cong1，ZHAO Bao-jun1，WANG Shui-gen1，WANG Hong-you3

(1.School of Information and Electronics， Beijing Institute of Technology， Beijing 100081， China; 2.Structure Health Monitoring and Control Institute, Shijiazhuang Tiedao University, Shijiazhuang, Hebei 050043, China;3.Baicheng Weapen Test Center， Baicheng， Jilin 137001， China)

In order to deal with the drawbacks of template drifting in small sample space and the bad real-time performance in large sample space with the tracking algorithm based on sparse representation model, a tracking approach based on double sparse representation and circle shape sampling was proposed. The image data obtained from tracking rectangular frame were sampled with circle shape sampling model, not only preserving grayscale and structure information of tracking object, but also cutting down the disturbance from background pixels. Meanwhile, the trivial template coefficients gotten from sparse representation were analyzed with a distance weighting function to be used for obtaining target sample changing condition and improving efficiency of template updating. Finally, HOG(histogram of oriented gradient)feature was introduced for once more sparse representation to the second-best sparse solutions, which can cut down estimation error in small sample space. Experimental results show that the proposed algorithm can improve the robustness and efficiency of object tracking in small sample space.

sparse representation; object tracking; template drifting

2014-03-10

国家“八六三”计划项目(2012AA8012011C)

王保宪(1987—)，男，博士，E-mail:wbx1025@163.com.

唐林波(1978—)，男，博士，讲师，E-mail:tanglinbo@bit.edu.cn.

TP 273.2

A

1001-0645(2016)09-0983-08

10.15918/j.tbit1001-0645.2016.09.019