从一道课本例题谈分式的化简求值问题
2016-11-23赵密密
赵密密
从一道课本例题谈分式的化简求值问题
赵密密
分式的化简求值是中考常考的类型,在2015年江苏省13个市的中考数学试卷中,9个市考查了化简或化简求值.而在全国的近两百份考试试卷中,出现化简求值题非常多.我们将从苏科版《数学》教材八年级下册第110页例3进行研究,希望大家获得解决此类问题的技巧与方法.
八年级下册110页例3

求分式的值,若分式的分子、分母是多项式时,应先将它们分解因式,然后将除法运算统一为乘法运算,约分后再代入数值计算.
例1如果实数x满足x2+2x-3=0,那么代数式的值为_______.
【分析】先将代数式化简,再对已知条件进行等式变形,可求出x2+2x的值,再整体代入所求代数式即可.
=x2+2x+2,
∵x2+2x-3=0,∴x2+2x=3,
∴原式=3+2=5.
【点评】求分式运算中代数式的值时,要通过化简,确定已知条件和化简结果的关系,最后观察分析求解.
(1)化简A;
【分析】(1)根据分式四则混合运算的运算法则,把A式进行化简即可.
(2)首先求出不等式组的解集,然后根据x为整数求出x的值,再把求出的x的值代入化简后的A式进行计算即可.
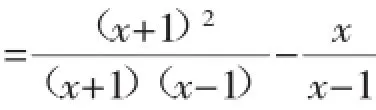
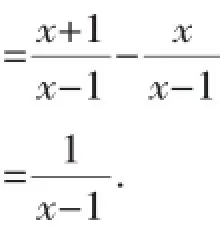
∴1≤x<3,
∵x为整数,
∴x=1或x=2,
①当x=1时,
∴x-1=0,
∵A式中分母为x2-1,x-1,
∴当x=1时,A无意义.
【点评】(1)此题主要考查了分式的化简求值,注意化简时不能跨度太大而缺少必要的步骤.
(2)此题还考查了求一元一次不等式组的整数解问题,要熟练掌握,解决此类问题的关键在于正确解得不等式组或不等式的解集,然后再根据题目中对于解集的限制得到下一步所需要的条件,再根据得到的条件求得不等式组的整数解即可.
【分析】原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,三个数中任选一个代入计算即可求出值(这里我们选3,注意:不能选1和2).
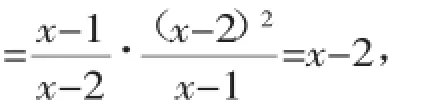
当x=3时,原式=3-2=1.
【点评】此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.
例4(2014·东营)如果实数x,y满足
【分析】原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,求出方程组的解得到x与y的值,代入计算即可求出值.
当x=3,y=-1时,原式=1.
故答案为:1.
【点评】此题考查了分式的化简求值及解二元一次方程组,熟练掌握运算法则是解本题的关键.
【分析】原式括号中两项通分并利用同分母分式的减法法则变形,同时利用除法法则变形,约分得到最简结果,求出已知方程的解得到m的值,代入计算即可求出值.
由m(m+1)=13m,解得m1=0,m2=12.
【点评】此题考查的是分式的化简求值及解一元二次方程,熟知分式混合运算的法则是解答问题的关键.
(作者单位:江苏省淮安外国语学校)
