运用数学思想方法巧解函数题
2016-11-23张俭衣
张俭衣
运用数学思想方法巧解函数题
张俭衣
函数相关的问题复杂多变,计算量大,若能在解题中灵活运用一些技巧,可大大减少计算量,提高解题速度,这对培养同学们解决问题的灵活性也大有帮助.下面就一些常用的技巧举例加以说明.
一、巧取特殊值
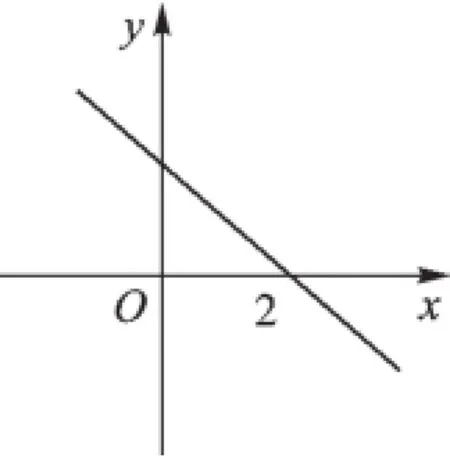
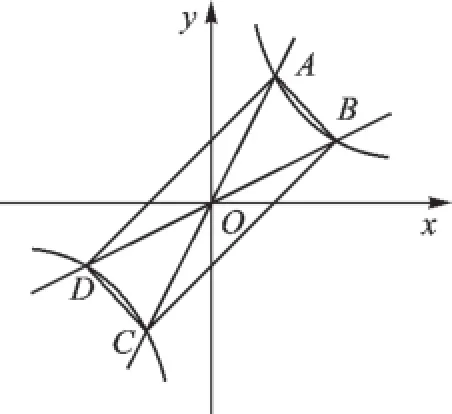
A.y1 C.y2 【分析】若直接利用反比例函数的性质去比较大小,由于图像上的三点不在同一个分支,容易出现错误.这里可以通过取特殊值转化为简单的计算进行比较. 【点评】在一些函数问题中,若对函数的自变量中所有值进行全面考虑,问题比较复杂.但若能取一些有代表性的特殊值,进行简化思考、计算,就能使解题快捷.但需要注意的是,所取的特殊值必须满足题目的条件. 例2已知y+m与x+n(其中m,n是常数)成正比例关系,且当x=-1时,y=-15;当x=7时,y=1,求y与x之间的函数关系式. 【分析】根据正比例函数定义可设出函数关系式,将条件代入后把多元的方程组问题通过添加括号成为二元一次方程组,使不便求解的问题得到解答. 解:设y+m=k(x+n)(其中m,n是常数,k≠0),∴y=kx+(kn-m). ∵x=-1时,y=-15;x=7时,y=1, ∴所求的函数关系式为y=2x-13. 【点评】当问题中出现若干个相同的部分或问题中关系式的个数少于未知数的个数时,可把一些有关系的量看作一个整体来处理. A.-6B.-9C.0D.9 【分析】利用正比例函数与反比例函数图像关于原点对称的特性,把两点坐标转换成一点的坐标再解答. 解:由函数图像的对称性知点A与点B关于原点对称, ∴x2=-x1,y2=-y1, 从而x1y2+x2y1=-x1y1-x1y1=-2x1y1. 故x1y2+x2y1=-6. 应选A. 【点评】利用对称性解题是指利用正比例函数图像、反比例函数图像关于原点对称的特性进行解题的一种技巧.当函数图像关于某直线对称时,也可用对称性进行巧妙解答. 例4已知一次函数y=(m+2)x+(1-m),y随x的增大而减小,且它的图像与x轴的交点在原点的右侧,则m的取值范围是____________. 【分析】因为y随x的增大而减小,直线从左向右呈下降趋势,它的图像又与x轴的交点在原点的右侧,根据题意画出相应一次函数图像,由图像列出不等式组并解之可求得m的范围. 解:由题意画出函数的示意图(如图1), 图1 解得m<-2. 【点评】数形结合是指利用图形来帮助解答一些代数问题的一种方法.在函数相关的问题中若涉及的内容较难或较繁可考虑利用图像的直观性来帮助思考;反之,一些图像问题也可用代数的办法加以解决. 小试身手 1.点P(x-1,x+1)不可能在(). A.第一象限B.第二象限 C.第三象限D.第四象限 2.不论数a取什么值,直线y=ax-2a+1总通过一个定点,这个定点的坐标为_______. 3.已知抛物线y=x2-x-1与x轴的一个交点为(m,0),则代数式-m2+m+2016的值为(). A.2014B.2015 C.2016D.2017 4.(2015·徐州)若函数y=kx-b的图像如图2所示,则关于x的不等式k(x-3)-b>0的解集为(). A.x<2B.x>2 C.x<5D.x>5 5.如图3,过原点的直线y=k1x和y=k2x与反比例函数的图像分别交于两点A,C和B,D,连接AB,BC,CD,DA.四边形ABCD的形状一定是_______. 图2 图3 7.已知x满足0≤x≤5,y1=x+2,y2=-2x+ 5,对任意一个x,y1,y2中的较大值用m表示,则m的最小值是_______. 参考答案 1.D2.(2,1)3.B4.C5.平行四边形6.37.3. (作者单位:江苏省宿迁市钟吾国际学校)二、巧用整体思想
三、巧用对称性
四、巧用数形结合