利用函数知识巧解规律探索题
2016-11-23王维松
王维松
利用函数知识巧解规律探索题
王维松

规律探索问题是中考常考题型,类型比较多,此类题型解法也多种多样,有一些规律探索问题根据数字规律,巧用函数知识可以很快解决.其关键是把变量和序号放在一起加以比较,就容易发现其中的奥秘.
一、巧用一次函数解题
例1有一列数:8,14,20,26,32,……,则第20个数是_______.
【解析】第一个数是8,由序号和对应的数值构成的点设为A,则A(1,8);
第二个数是14,由序号和对应的数值构成的点设为B,则B(2,14);
第三个数是20,由序号和对应的数值构成的点设为C,则C(3,20).
设第n个数为y=kn+b,
把A(1,8),B(2,14)分别代入y=kn+b中得:解得:k=6,b=2,用C点检验,符合题意,正确.
所以规律为y=6n+2.取n=20,则y=122.
【点评】我们发现相邻之间的数据差相等,便可运用一次函数求解规律探索问题,只要把序号作为自变量,每个变量作为函数值,用待定系数法就可以解决.
例2用边长为1 cm的小正方形搭成如下的塔状图形,则第n次所搭图形的周长是_______cm(用含n的代数式表示).
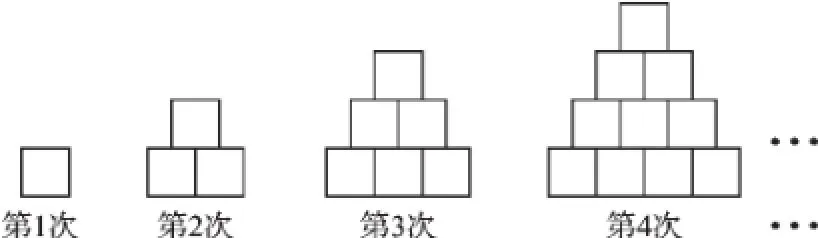
【解析】第一个图周长是4 cm,由序号和对应的数值构成的点设为A,则A(1,4);
第二个图周长是8 cm,由序号和对应的数值构成的点设为B,则B(2,8);
第三个图周长是12 cm,由序号和对应的数值构成的点设为C,则C(3,12).
设第n个图形的周长为y=kn+b,
把A(1,4),C(3,12)分别代入y=kn+b中得:解得:k=4,b=0,
用B点检验,符合题意,正确.
所以规律为y=4n.
即第n次所搭图形的周长是4n cm.
【点评】对于此类型的题目,我们应该先观察图形排列顺序的规律,然后把它们转化为相应的数据,并根据规律用函数模型表示图形的数量关系、变化规律加以解答.
二、巧用二次函数解题
例3有一列数1,3,6,10,15,21,……,第50个数是_______.
【解析】本题中数列的数字,不容易发现其变化的规律,我们不妨利用函数的思想去试一试.
当序号为1时,对应的值是1,由序号和对应的数值构成的点设为A,则A(1,1);
当序号为2时,对应的值是3,由序号和对应的数值构成的点设为B,则B(2,3);
当序号为3时,对应的值是6,由序号和对应的数值构成的点设为C,则C(3,6).
对应的数值y是序号n的二次函数,因此,我们不妨设y=an2+bn+c.
把A(1,1),B(2,3),C(3,6)分别代入y=an2+bn+c中,得:

检验:当x=4时,y=10,正确.
∴第50个数是1275.
【点评】一组数据,每相邻两个数据作差得到的新数据等差,如果是4组以上的数据,就可以任取三个数据,用函数关系y= ax2+bx+c列出方程组,分别求出a、b、c的值,再将第四组数据代入验证,如果不正确,说明不能用函数找规律.
例4下图中的实心点个数分别为1,5,12,22,……被称为五角形数,若按此规律继续下去,则第n个五角形数m是_______.
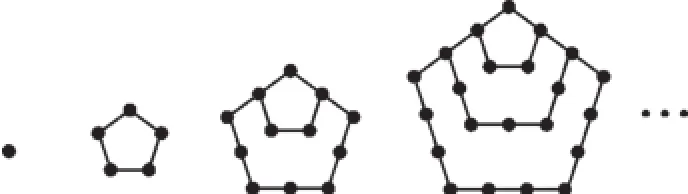
【解析】观察图形的序号与点数有下列关系:
序号:1234……
点总数:151222……
设m与n的函数解析式是m=an2+bn+c
【点评】解题时,如果题中隐去了序列号,要加上序列号,以便列出方程组求解.
三、运用其他类型函数解题
例5观察下列图形(每幅图中最小的三角形都是全等的),请写出第n个图中最小的三角形的个数有()个.

A.4nB.3n-2
C.n4D.4n-1
【解析】观察本图形,会发现序号与三角形个数关系十分复杂,但根据所给选项知道结果是幂的形式,且呈现以下规律:
序号:1234……
点总数:1222426……
设三角形的个数为y=2an+b,代入上述两组数据,得
解这个方程组得:a=2,b=-2,
检验:当x=3时,y=16,正确.
∴第n个图中最小的三角形的个数为y=22n-2=4n-1,选D.
【点评】一般地运用an类型函数求解的“找规律”题,我们发现相邻之间的数据商相等.
(作者单位:江苏省宿迁市钟吾国际学校)
