利用对称性,巧解函数题
2016-11-23袁彩辉
袁彩辉
利用对称性,巧解函数题
袁彩辉
在初中数学中,函数的对称性主要指的是函数图像的对称性,一般指中心对称性和轴对称性.初中阶段学习的正比例函数、反比例函数、二次函数都具有对称性.许多中考函数题,特别是一些选择题或填空题,如果利用对称性,可化繁为简,从而获得巧妙的解法,有的甚至能直接得出结果,回避常规解法的大计算量与繁杂过程.下面举例说明,供同学们参考.
一、巧用正比例函数与反比例函数的对称性
1.求特殊关系点的坐标
A.(1,3)B.(-1,-3)
C.(-3,-1)D.(-2,-3)
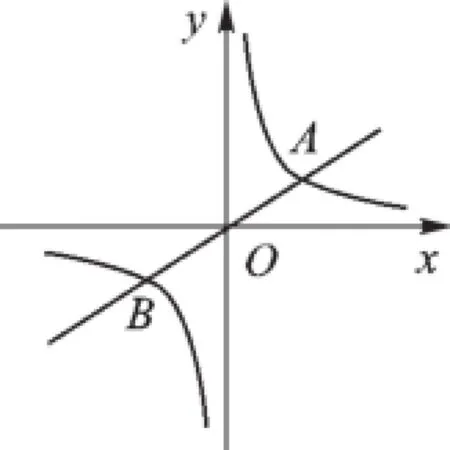
图1
【解析】本题一般可以采用待定系数法求出正比例函数和反比例函数的解析式,然后再求出两函数图像的交点.但如果能够利用反比例函数和正比例函数都是中心对称图形,A、B两点以原点(0,0)为对称中心,那么B点坐标便容易求出.故本题选C.
2.求特殊图形的面积
例2如图2,正比例函数和反比例函数的图像相交于A、B两点.分别以A、B两点为圆心,画出与y轴相切的两个圆.若点A的坐标为(1,2),则图中两个阴影部分面积的和是_______.

图2
【解析】分别求两个阴影部分面积显然不可行.由于正比例函数与反比例函数图像都关于原点对称,可知A、B两点关于原点对称.从而⊙A与⊙B也关于原点对称,故阴影部分面积和等于⊙A(或⊙B)的面积.⊙A与y轴相切,则⊙A的半径为1.故阴影部分的面积和等于π×12=π.
3.求代数式的值
高校档案馆的服务不能停留在传统的服务功能,新时代应该有新气象新作为,站在新的历史起点上,高校档案馆要大力加强阵地建设;构建具有高校人文特色的档案资源体系;从高校档案文化建设的角度拓展档案资源开发利用;把握好高校档案信息化建设的长远性和可操作性;发挥优势为档案事业发展培养更多的专业人才。
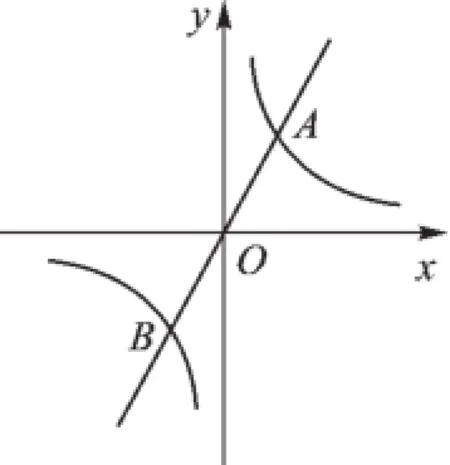
图3
【解析】通过上面例子,大家肯定会发现本题如利用对称性解会更简单.由中心对称性知A、B两点关于原点对称,则x1=-x2,y1=-y2.
∵A、B两点在双曲线上,
∴x1y1=4,x2y2=4,
∴2x1y2-7x2y1=-2x1y1+7x2y2=-2×4+7×4=20.
二、巧用反比例函数?图像的对称性

图4
三、巧用二次函数的对称性
例5小颖在二次函数y=2x2+4x+5的图像上,依横坐标找到三点(-1,y1),(0.5,y2),(-3.5,y3),你认为y1,y2,y3的大小关系应为().
A.y1>y2>y3B.y2>y3>y1
C.y3>y1>y2D.y3>y2>y1
【解析】本题可以把x的值代入函数求出对应的y的值,但这样计算量会很大,如果能够利用二次函数的对称性本题就会省去很多的计算过程了.由题可知该抛物线的对称轴为x=-1,所以x=0.5时的函数值与x=-2.5时的函数值相等,再利用二次函数的增减性可得出y3>y2>y1.故选D.
2.利用抛物线的对称性求抛物线的对称轴和与x轴的交点坐标
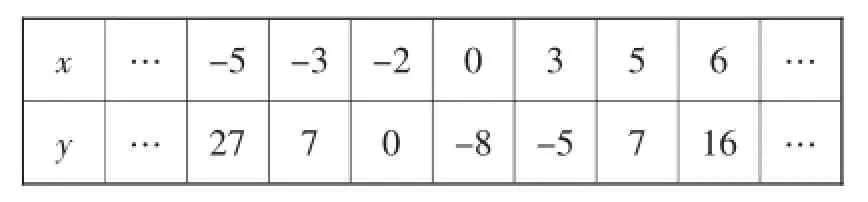
例6下表是二次函数y=ax2+bx+c(a≠0)的函数值y与自变量x的对应值.
x…-5-3-20356…y…2770-8-5716…
(1)找出抛物线上关于对称轴对称的两点_______、_______.
(2)写出抛物线的对称轴_______,抛物线与x轴的交点坐标是_______.
【解析】本题的常规做法是先求出解析式,然后解出抛物线与x轴的交点,并求出其对称轴.但若能掌握抛物线是轴对称图形,由表中当x=-3和x=5时的函数值都是7,可知这两点的连线平行于x轴,故被对称轴垂直平分,所以这两点关于对称轴对称,从而得出抛物线的对称轴为x=1.再由当x= -2时y=0可知抛物线与x轴的另一个交点为(4,0).
3.利用抛物线的对称性求最短距离
例7如图5,抛物线y=0.5x2+bx-2与x轴交于A,B两点,与y轴交于C点,顶点为D,且A(-1,0).若点M是对称轴上的一个动点,当MC+MA的值最小时,求M点的坐标.
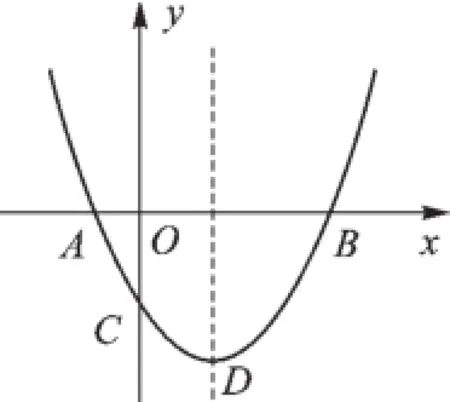
图5
【解析】本题若按题意可先来解出抛物线解析式,并求出其对称轴,然后设出点M的纵坐标,利用勾股定理表示出MC和MA的长,最后利用二次函数求最大(小)值的方法求出对应的M点的坐标.但若利用抛物线的对称性可知,由于点M在对称轴上,所以MA=MB.本题就转化为求MC+MB的最小值了,那么求出直线BC的解析式再代入对称轴的横坐标即可.
函数的对称性是函数本身内在的特性,若能灵活恰当地应用好函数的这一性质,会给解题提供意想不到的帮助.
(作者单位:江苏省宿迁市钟吾国际学校)
