梯形断面消力池扩散型消能计算

黄朝煊

（浙江省水利水电勘测设计院，浙江杭州 310002）

梯形断面消力池扩散型消能计算

黄朝煊

（浙江省水利水电勘测设计院，浙江杭州 310002）

针对目前NB/T35023—2014《水闸设计规范》只涉及矩形断面消力池，未涉及梯形断面消力池消能计算的问题，基于水力学基本理论和数值分析理论对梯形断面消力池消能计算进行研究，推导了梯形断面收缩水深的解析计算式以及梯形断面消力池扩散型消能跃后共轭水深基本方程，并利用高次方程求解理论分别给出棱柱体梯形断面跃后共轭水深的解析计算式和扩散型消能跃后共轭水深的简易迭代求解公式，并根据消能计算方程，给出梯形断面消力池扩散型消力池池深、池长的计算式。工程实例计算结果表明，所提出计算式精度可靠。

消力池；水闸；梯形断面；收缩水深；跃后共轭水深；扩散比

水闸消能计算为消能防冲设计的基础，关系到水闸整体的安全稳定性，随着国家对农田水利发展的重视、“五水共治”以及“海绵城市”理念的提出，水闸消能计算显得尤为重要。目前NB/T 35023—2014《水闸设计规范》［1］只对矩形断面消力池消能计算进行说明，而实际工程有采用梯形翼墙断面的情况，如舟山市六横小郭巨围垦工程挡潮排涝闸［2］。对于梯形翼墙断面消能计算，往往采用面积等效法将其近似为矩形断面，但该近似等效法误差较大，不能保证实际工程的消能防冲安全。已有文献中，主要是针对矩形断面消力池消能计算进行研究，如黄朝煊等［3］对矩形断面消力池池深极值进行了无量纲化数学推导，得出了矩形断面消力池池深极值的直接计算公式；谢景惠等［4］对矩形断面消力池池深计算进行了微分极值初步推演，但不具备实际应用价值。田嘉宁等［5-7］采用智能算法如遗传算法（GA）和粒子群算法（SPO）等对多级消力池总长等参数进行了程序优化，其原理与罗列多工况试算法基本一致，无法寻找本质共性特征。田嘉宁等［8］、刘璐等［9］通过模型试验分别对台阶式消能和联合型消能消力池的水力特性进行了研究，也不能得出共性规律。为弥补目前水闸消能计算仅适用于矩形断面的不足，笔者基于数学分析理论，拟结合Matlab软件对梯形断面消力池扩散型消能计算进行研究，得出消力池池深、池长的解析计算式。

1　消能计算基本理论

如图1所示，消力池消能计算基本公式为

式中：d为消力池池深；σ0为水跃淹没系数，可取1.05～1.10；h2为跃后水深；hs为下游水深；ΔZ为出池落差；T0为以收缩断面底部为基准面的泄水建筑物上游总水头；h1为跃前收缩断面水深；Q为流量；g为重力加速度；φ为流速系数；A1为收缩断面过水面积；As为下游河床过水断面面积；A2为跃后过水断面面积；α为水流动能校正系数，可采用1.0～1.05；Lsj为消力池池长；Ls为消力池斜坡段水平投影长度；Lj为水跃长度；β为水跃长度校正系数，取值0.7～0.8。

图1　水闸消力池消能计算示意图

2　跃前收缩水深计算

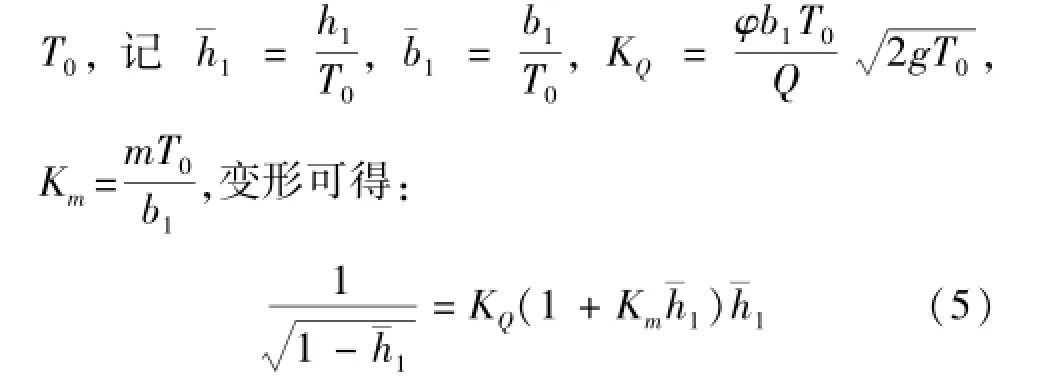
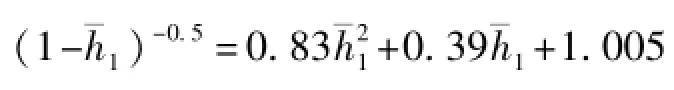
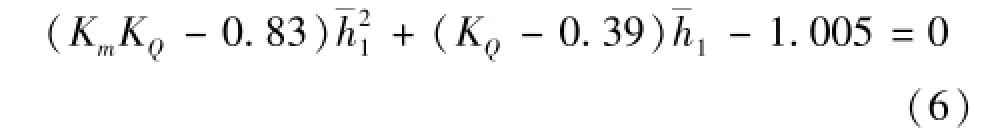
根据无量纲化理论可知KQ≥2.25，0＜Km＜3。公式（6）的判别式Δ=（KQ-0.39）2+4.02（KmKQ-0.83）＞0，求解一元二次方程，得跃前收缩断面无量纲水深的直接计算式为

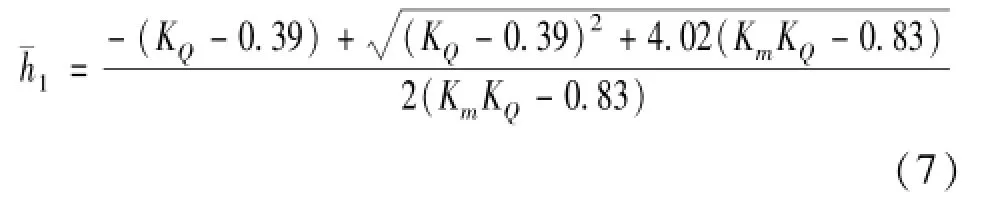
通过数值计算研究，公式（7）的适用范围为0＜h1/T0＜0.5。一般水利工程中总水头远大于收缩断面水深，因此公式（7）在绝大部分情况下是适用的。

采用Matlab软件迭代算法求解非线性方程，得到精确值，可知公式（7）的最大相对误差小于0.57%（图2），精度完全满足工程计算要求。h1/T0与KQ、Km关系曲面见图3。

图2　公式（7）相对误差分布曲线

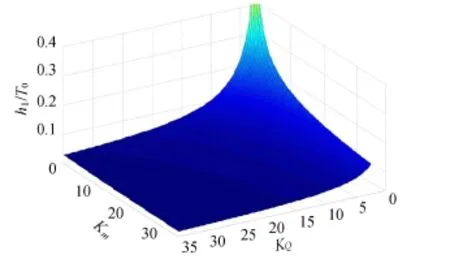
图3　h1/T0与KQ、Km关系曲面

3　跃后共轭水深计算

如图4所示，利用连续方程和动量方程推导得扩散型梯形翼墙断面水跃方程为

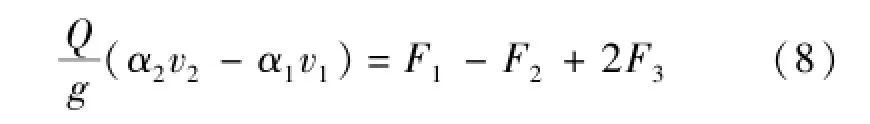
式中：v1、v2分别为跃前断面和跃后断面平均流速；α1、α2分别为跃前断面和跃后断面流速系数；F1、F2分别为跃前断面和跃后断面顺水流轴线方向作用力；F3为扩散段翼墙水压力在顺水流轴线方向的投影分量。

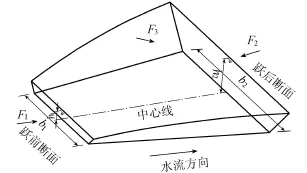
图4　扩散型梯形断面消能示意图

根据水压力计算理论可知：

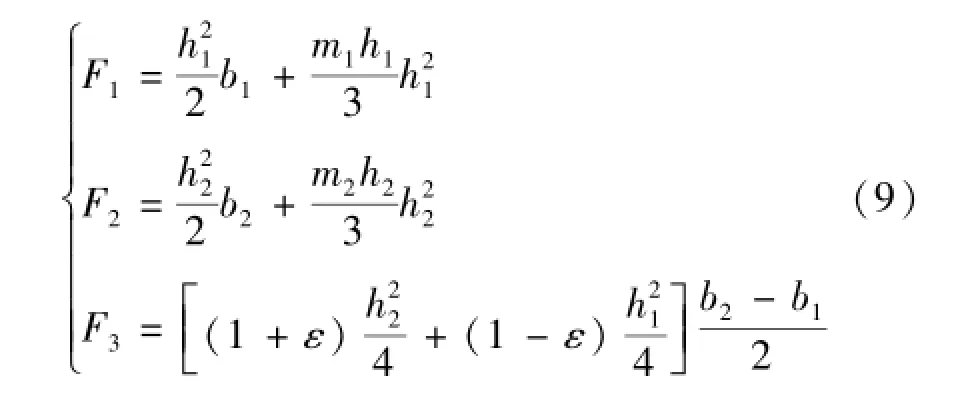
式中：ε为水跃过程中水面线的非线性变化的影响系数，ε≥0，本文取ε=0；m1、m2分别为跃前断面和跃后断面坡比；b1、b2分别为跃前收缩断面和跃后断面的底宽。取m1=m2=m，α1=α2=1，记跃后无量纲相对水深η2=mh2/b2，跃前无量纲相对水深η1= mh1/b1，记扩散比ξ=b1/b2。将公式（9）代入公式（8）化简可得：

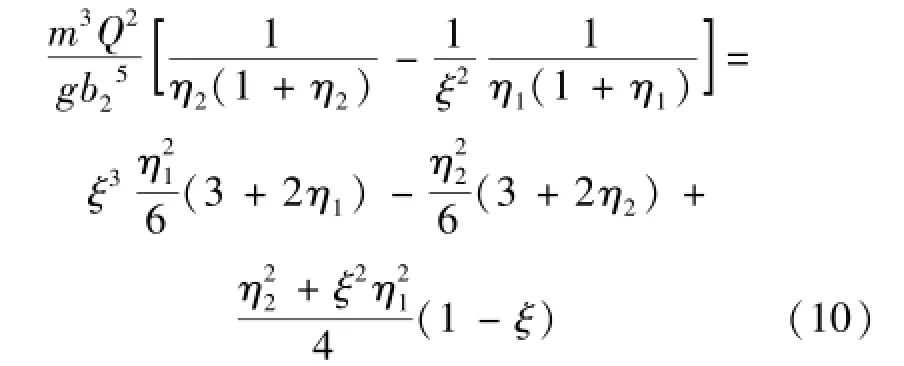
公式（10）即为用η2表征的跃后共轭水深计算方程，该方程也是一元五次方程，一般情况下无法直接求解。

3.1无扩散时（ξ=1）跃后共轭水深计算

对无扩散时梯形断面共轭水深的计算，刘计良等［10］给出了近似计算法，但精度不高，其中最大跃后水深相对误差甚至大于5%。笔者拟根据数学方程理论，给出跃后共轭水深精确解析解。

对于无扩散情形，即b1=b2=b，ξ=1，公式（10）可进一步简化为以下关于无量纲相对水深η1、η2的轮换对称方程：

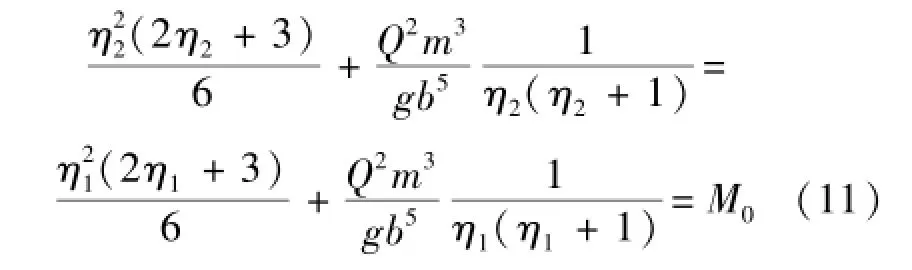
式中M0为中间参数。易知公式（11）是对称方程，η1、η2均是该一元五次对称方程的实根，由跃前收缩水深计算跃后共轭水深时，可将公式（11）除以（η2-η1）进而转化为一元四次方程，根据《特殊函数概论》［14］中推荐的一元四次方程求解方法，求解步骤为：①通过对待求变量x作平移变换，将一般一元四次方程的三次方项系数转换为零；②通过待定系数法和因式分解理论将以上方程降次转换为两个一元二次方程的乘积形式，进而求出原一元四次方程的解析解。

η1、η2为待求量，记K0=Q2m3/（gb5），t=η2-η1，将其代入公式（11），根据轮换对称方程的对称性，显然t=η2-η1=0（即η2=η1）是该方程的一个特解，可知关于t的五次方程常数项为零；方程两边同除以t，可转化为四次方程：

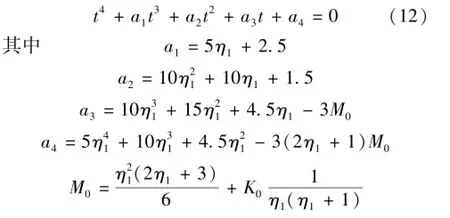
通过变量参数变换，设z=t+a1/4，进行因式分析得：

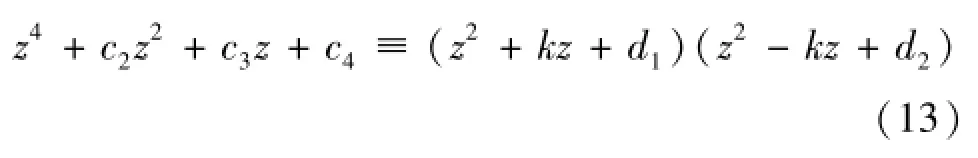
其中

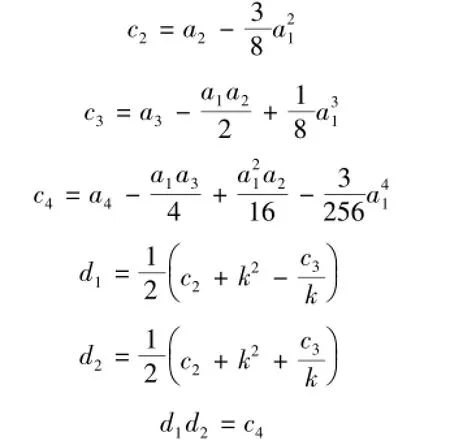
式中k为待求中间参数。

通过恒等关系消元变换得待定系数k2满足以下三次方程：

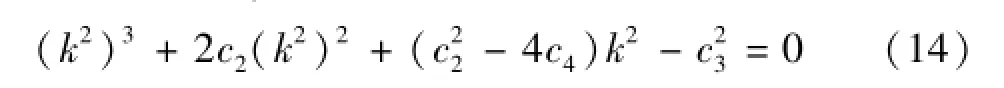
利用卡当公式求解方程（14），可得待定系数k2的正实根为

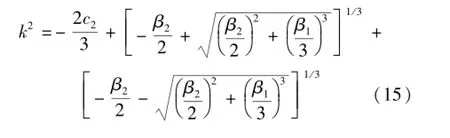
将方程（15）代入方程（13）右边的因式分解项，将方程（13）降次为两个一元二次方程，求解得正根z，并根据上述参数代换z=t+a1/4，t=η2-η1，求解得跃后共轭水深的精确解析计算式为

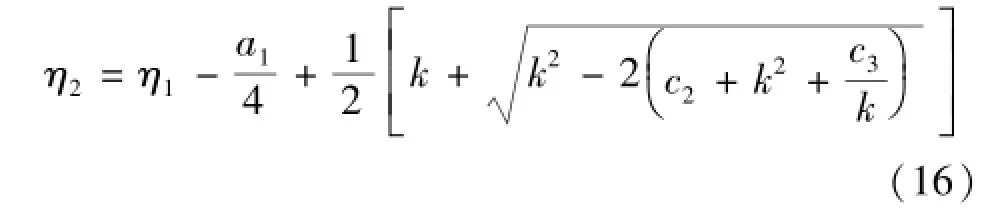
公式（16）适用于棱柱体梯形断面水跃情况。通过公式（16）可直接给出简化后的数值解集，记收缩断面处的临界水深为hk1，则其无量纲量ηk1= mhk1/b1，ηk1的解析式已有较多研究，如文献［11-13］，可采用现有公式计算。记参数x=η1/ηk1，y= η2/ηk1，x=1时为临界情况，此时x=y=1，η1=η2= ηk1；根据水跃强弱知Fr≤9，通过Matlab软件反分析得到0.23≤x≤1，考虑到更广的适用范围，本文分析0.15＜x≤1的范围。

根据以上解析法可求出x、y随K0之间的精确数据关系（表1），通过分析可知，当0.2＜K0＜8时，x、y随K0的影响不敏感（最大相对误差小于0.85%），直接根据跃前水深x求出跃后水深y，进而根据y=η2/ηk1求出跃后无量纲相对水深η2。

通过最佳逼近拟合原理，得出无扩散时（ξ=1）用y表征的跃后共轭水深的近似计算公式：

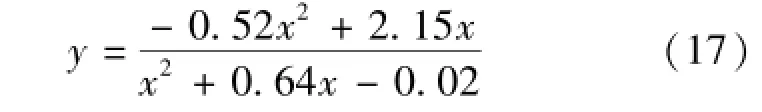
式（17）适用于0.2≤K0≤8时的棱柱体梯形断面水跃计算，当K0＜0.2或K0＞8时，计算误差为3.5%，相对较大。

3.2扩散型消能（0.5＜ξ＜1）跃后共轭水深计算

对于扩散型消能，b1≠b2，记无量纲参数K′0=

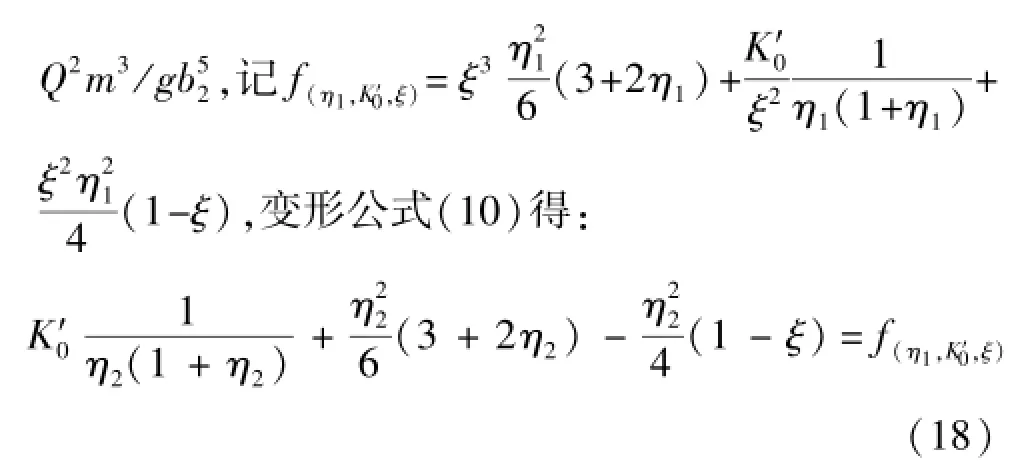
方程（18）为η2的一元五次方程，其中无量纲参数K′0、η1、ξ均为已知参数。由于该方程较复杂，无法直接求解，可采用迭代法将方程（18）变换成如下形式：

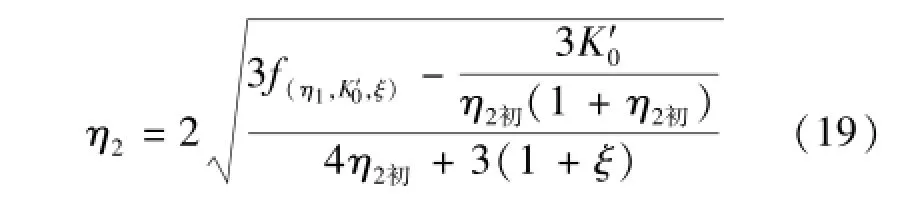
通过对公式（19）右边求导容易证明其导数绝对值小于1，即迭代方程（19）收敛，限于篇幅，本文未给出证明过程。其迭代初值η2初可根据无扩散时（ξ=1）跃后共轭水深计算式（17）的修正值（乘以修正系数ξ）给出，公式如下：

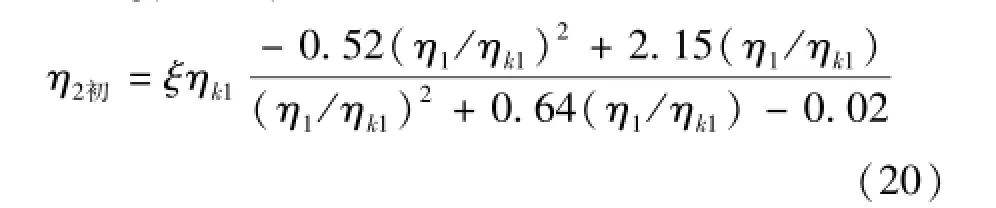
其中收缩断面处的临界水深的无量纲量可采用王正中等［11］的计算公式：

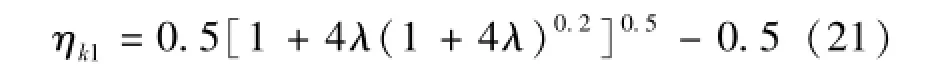
通过Matlab软件大量数值计算分析可知公式（21）的相对误差小于0.5%，甚至接近0.01%，精度很高。η2的迭代初值计算公式（20）精度也较高，公式（20）与精确值的比值函数曲面见图5。通过迭代公式（19）迭代1次后精度基本小于1%，满足实际工程计算要求。

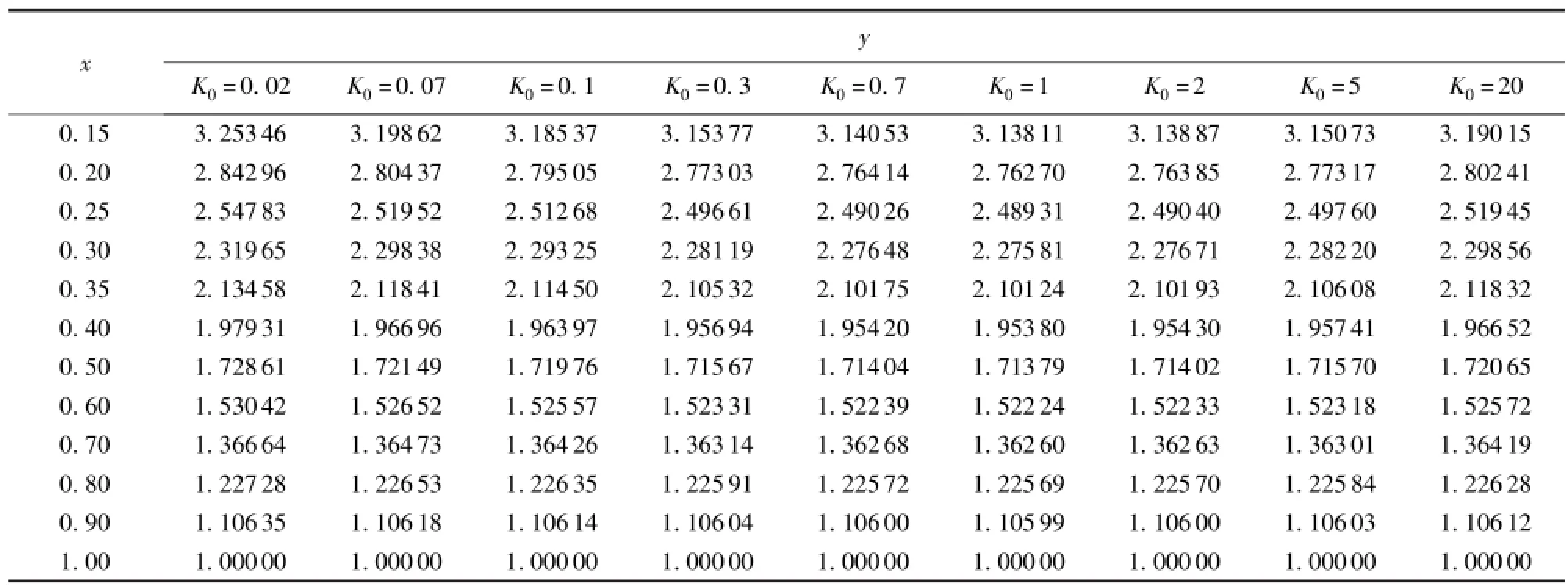
表1　由共轭水深公式（16）求解出的y与x、K0关系

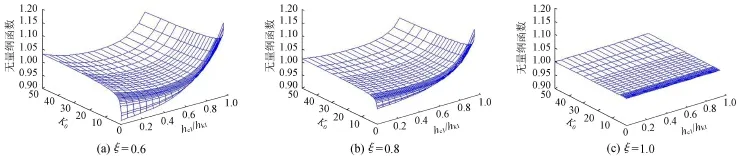
图5　公式（20）与精确值的比值函数曲面

4　算例分析

某闸前断面总水头T0=10.31 m，过闸流量Q= 140 m3/s，下游水深hs=4.0 m。梯形翼墙消力池断面底宽b1=10 m，b2=12.5 m，梯形翼墙边坡系数m=1，流速系数φ=0.95，需求解该工况下闸下消力池池深和池长。

步骤1 求解跃前收缩断面水深h1。根据KQ= 9.9452，Km=1.031，将其代入公式（7）得¯h1=0.09613，进而可得h1=¯h1T0=0.096 13×10.31 m=0.991 1 m，与Matlab软件采用多次迭代法算得的精确值0.9915m基本一致，相对误差为0.043%。

步骤2 求解跃后水深h2。根据h1=0.9911 m，η1=0.099 11，λ=0.2714，由公式（21）可知ηk1= 0.2492，进而得到x=η1/ηk1=0.397 8，根据公式（20）可知η2初=0.391 3，计算得出K′0=0.006 55，f（η1，K′0，ξ）=0.097 0，根据迭代公式（19），由η2初= 0.3913迭代1次后得η2迭1=0.3826，与Matlab软件多次迭代法算得的η2=0.3827基本一致，精度相当高，进而得到h2=η2b2/m=4.782 m。

步骤3 求解消力池池深、池长。根据h1= 0.9911m，h2=4.782 m，hs=4.0 m，由消能计算公式（3）及A=（b+mh）h可知ΔZ=0.1725 m，故可知该工况下消力池池深d=σ0h2-hs-ΔZ=1.05×4.782 m-4.0 m-0.1725 m=0.849 m，进而由公式（4）知该工况下消力池池长Lsj=23.47 m。

另外，若采用面积等效法将梯形断面近似为矩形断面，根据黄朝煊等［3］矩形断面消能研究成果可知，矩形断面翼墙最不利条件下消力池池深极值可采用以下公式计算：

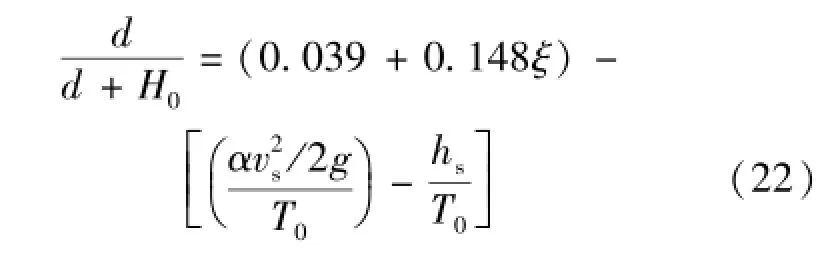
求解该方程可知消力池池深极值dmax=1.688 m，比本文扩散型梯形翼墙消力池特定工况下的消力池池深计算值0.849 m大，因此，笔者认为扩散型梯形断面消力池也同矩形断面消力池一样，存在某种最不利工况使得消力池池深取极大值，同样，消力池池长也存在一个极大值。鉴于问题的复杂性，笔者将进行后续研究。

5　结 语

a.通过水力学基本理论及数值分析理论对梯形断面消力池消能计算进行分析研究，通过降次法推导出了收缩水深解析计算公式，该公式精度满足工程计算要求。

b.根据动量守恒定律推导了梯形断面消力池扩散型水跃共轭水深基本方程，并通过一元四次方程求解理论给出了无扩散（ξ=1）梯形断面跃后水深的解析计算式；同时给出了扩散型（0.5＜ξ＜1）梯形断面跃后水深的快速收敛迭代计算式，并通过算例分析，认为本文计算公式精度可靠，方便快捷。

c.根据本文给出的梯形断面收缩水深、跃后共轭水深解析计算式以及消能基本方程，得到了梯形断面扩散型消能的消力池池深、池长的计算方法，为工程设计提供理论基础。

［1］NB/T 35023—2014 水闸设计规范［S］.

［2］舟山市六横小郭巨围垦工程初步设计［R］.杭州：浙江省水利水电勘测设计院.2010.

［3］黄朝煊，王贺瑶，王正中，等.消力池最不利条件下池深极值探讨［J］.水力发电学报，2015，34（1）：79-84.（HUANG Chaoxuan，WANG Heyao，WANG Zhengzhong，et al.The investigate for extremum depth of sluice stilling basin under the most unfavorable conditions［J］.Journal of Hydroelectric Engineering，2015，34（1）：79-84.（in Chinese））

［4］谢景惠，陈菊清.消力池最不利设计条件的分析与计算［J］.水利水电技术，1995（12）：7-11.（XIE Jinghui，CHEN Juqing.Analysis and caleulation of the most unfavourable design conditions for stilling basin［J］.Water Conservancy and Hydropower Engineering，1995（12）：7-11.（in Chinese））

［5］田嘉宁，安田阳一，李建中.台阶式泄水建筑物的消能分析［J］.水力发电学报，2009（2）：96-100.（TIAN Jianing，YASUDAYouichi，LIJianzhong.Energy dissipation on stepped sluicing structure［J］.Journal ofHydroelectricEngineering，2009（2）：96-100.（in Chinese））

［6］BAKHTYAR R，BARRY D A.Optimization of cascade stilling basins using GA and PSO approaches［J］.Journal of Hydroinformatics，2009（11）：119-132.

［7］BAKHTYAR R，MOUSAVI S J，AFSHAR A.Dynamicprogramming approach to optimal design of cascade stilling basins［J］.Journal of Hydraulic Engineering，2007，133（8）：949-954.

［8］田嘉宁，赵庆，范留明.台阶式溢流坝后消力池压强特性［J］.水力发电学报，2012，31（4）：114-124.（TIAN Jianing，ZHAOQing，FANLiuming.Pressure characteristics in stilling basin of stepped spillways［J］. Journal of Hydroelectric Engineering，2012，31（4）：114-124.（in Chinese））

［9］刘璐，张建民，余飞，等.重力坝下游宽尾墩和消力池联合消能工水力特性试验研究［J］.水力发电学报，2012，31（2）：49-55.（LIU Lu，ZHANG Jianmin，YU Fei，et al. Experimental study of hydraulic characters of the flaring gate pier&ling basin united energy dissipator with high water head and large discharge［J］.Journal of Hydroelectric Engineering，2012，31（2）：49-55.（in Chinese））

［10］刘计良，王正中，杨晓松，等.梯形渠道水跃共轭水深理论计算方法初探［J］.水力发电学报，2010，29（5）：216-219.（LIUJiliang，WANGZhengzhong，YANG Xiaosong，et al.Preliminary study on the theoretical method for calculating conjugate depth of trapezoidal channel［J］.Journal of Hydroelectric Engineering，2010，29（5）：216-219.（in Chinese））

［11］王正中，袁驷，武成烈.再论梯形明渠临界水深计算法［J］.水利学报，1999，30（4）：14-17.（WANG Zhengzhong，YUAN Si，WU Chenglie.A final inquiry on a formula for calculating critical depth of open channel with trapezoidal crosssection［J］.JournalofHydraulic Engineering，1999，30（4）：14-17.（in Chinese））

［12］黄朝煊.梯形明渠水力学特征水深的解析计算式研究［J］.灌溉排水学报，2016，35（3）：73-78.（HUANG Chaoxuan.Analytic formula of characteristic depths for trapezoidal open channel［J］.Journal of Irrigation and Drainage，2016，35（3）：73-78.（in Chinese））

［13］黄朝煊.梯形渠道恒定渐变流水面线计算的新解析法［J］.长江科学院学报，2012，29（11）：46-49.（HUANG Chaoxuan.A new analytical method of computing water surface curve of constant and gradually varied flow in trapezoidal channel［J］.JournalofYangtzeRiver Scientific Research Institute，2012，29（11）：46-49.（in Chinese））

［14］王竹溪，郭敦仁.特殊函数概论［M］.北京：北京大学出版社，2010：480-483.

Energy dissipation calculation for diffused stilling basin with trapezoidal cross section

HUANG Chaoxuan
（Zhejiang Design Institute of Water Conservancy and Hydro-Electric Power，Hangzhou 310002，China）

As the current standard NB/T 35023—2014“sluice design specification”involves stilling basin with rectangular cross section，excluding stilling basin with trapezoid section，energy dissipation calculation for stilling basin with trapezoidal cross section were studied on the basis of the classical hydraulics theory and numerical analysis.The analytical formula of shrinking depth and the equation of conjugate depth after hydraulic jump of stilling basin with trapezoidal cross section were derived.Using theory of high-order equation，simple iterative formulas for conjugate depth after hydraulic jump of stilling basin with prismatic trapezoidal cross section and diffused trapezoidal cross section were given，respectively.Finally，the calculation formulas for depth and length of the stilling basin with trapezoidal cross section were obtained according to the energy dissipation equation.Calculation results of a practical project validate the proposed formula has high accuracy.

stilling basin；sluice；trapezoidal cross section；shrinking depth；conjugate depth after hydraulic jump；diffusion ratio

TV131.4

A

10067647（2016）05003406

10.3880/j.issn.10067647.2016.05.006

水利部公益性行业科研专项（201401010）；浙水院科标业项目（B1608，B1609）

黄朝煊（1983—），男，硕士，主要从事水工结构及岩土工程研究。E-mail：516227811@qq.com

（20150723 编辑：骆超）