基于梯形模糊数联系数的评价方法及其应用

潘争伟，金菊良，周戎星

（1.安徽新华学院土木与环境工程学院，安徽合肥 230088；2.安徽新华学院安全与环境评价研究所，安徽合肥 230088；3.合肥工业大学土木与水利工程学院，安徽合肥 230009；4.合肥工业大学水资源与环境系统工程研究所，安徽合肥 230009）

基于梯形模糊数联系数的评价方法及其应用

潘争伟1，2，金菊良3，4，周戎星1

（1.安徽新华学院土木与环境工程学院，安徽合肥 230088；2.安徽新华学院安全与环境评价研究所，安徽合肥 230088；3.合肥工业大学土木与水利工程学院，安徽合肥 230009；4.合肥工业大学水资源与环境系统工程研究所，安徽合肥 230009）

针对当联系分量系数取值具有峰值较宽的分布特征时，利用三角模糊数表示差异度系数可能存在误差较大的问题，通过分析差异度系数取值与等级标准阈值的对应关系，确定了差异度系数的最优取值区间，构造了以梯形模糊数表示的差异度系数，提出了基于梯形模糊数联系数的评价方法。将该评价方法应用于巢湖流域水资源系统脆弱性评价，结果表明：置信水平75%条件下巢湖流域水资源系统脆弱性等级置信区间为［2.89，3.44］；所提出的方法不仅能得出评价等级的置信区间，有效避免差异度系数峰值较宽时产生的误差，还可以采用“期望方差排序法”对不同子区域的脆弱性等级进行优劣排序。

联系数；梯形模糊数；水资源系统；脆弱性评价；巢湖流域

集对分析方法利用联系数刻画研究问题，联系数的差异度系数在区间［-1，1］连续取值过程中具有明显的模糊性特征，与正态分布近似的三角模糊数能有效处理这种模糊性信息［1-2］。根据差异度系数取值的连续性，笔者曾构造了差异度系数的三角模糊数~A，建立了基于三角模糊数的联系数评价模型［3-4］。在水资源与水环境、水利工程等应用方面，汪哲荪等［2］建立了三角模糊数随机模拟的防洪工程联系数风险评价模型，并将其应用于防洪工程系统风险评价；潘争伟等［4］建立了基于三角模糊联系数的系统综合决策模型，并将其应用于安徽省水环境系统脆弱性评价；杨淇翔等［5］针对受多种不确定性因素影响的地下水环境质量评价问题，建立了集对分析与三角模糊数耦合的地下水环境质量评价模型；彭涛等［6］采用基于集对分析与三角模糊数耦合的方法对滨海湿地生态系统健康进行了评价。然而，进一步对联系分量系数取值与等级标准阈值对应关系的分析表明，等级标准g的联系分量系数存在最优取值区间，而当联系分量系数取值具有峰值较宽的分布特征时，可能导致基于三角模糊数的联系数存在较大误差［1，7］，为此，本文构造梯形模糊数表示差异度系数，提出了基于梯形模糊数联系数的评价方法。

1　基于梯形模糊数联系数的评价方法

1.1方法基础

1.1.1联系数

集对分析方法的基础是确定联系数，联系数的基本表达式［8］为

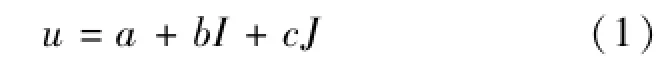
式中：a、b、c分别为集对的同一度、差异度和对立度，取值区间为［0，1］，且a+b+c=1；I为差异度系数，取值区间为［-1，1］，有时仅起差异标记作用；J为对立度系数，取值规定为-1，有时仅起对立标记作用。

式（1）建立在对描述对象作“同、异、反”划分的基础上，称为同异反联系数或三元联系数［8］。实际应用中，仅对描述对象所处的状态空间做一次“同、异、反”的划分尚不够细化，往往需要对联系数基本表达式作更深层次的扩展［9-10］，形成一种多元联系数：

1.1.2梯形模糊数

如图1所示，实数域R上的梯形模糊数［1］~A=（a，b，c，d），当a＜b=c＜d时，~A为三角模糊数，当a= b=c=d时，~A为一实数。

1.1.3置信水平区间

设梯形模糊数~A=（a，b，c，d），取置信水平α∈［0，1］，可以得置信水平区间［1］（图1）：

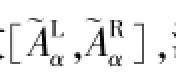
图1　梯形模糊数及其α截集

1.2方法的分析步骤

根据同异反分析的基本步骤［10］和系统评价方法分析的一般步骤［13］，基于梯形模糊数联系数的评价方法的分析步骤如下：

步骤1：分析所论评价问题，结合实际确定评价对象的指标体系。评价对象的样本i子系统j指标k的样本数据为xijk（i=1，2，…，n；j=1，2，…，m；k= 1，2，…，Nj），等级评价标准为sgjk（g=1，2，…，G；j= 1，2，…，m；k=1，2，…，Nj）；各指标的样本值xijk组成集合Ak，该指标等级g的标准阀值sgjk组成集合Bk，则由集合Ak与Bk构造一个集对H（Ak，Bk）。其中n、m、Nj和G分别为评价样本数目、子系统数目、子系统j的评价指标数目和评价等级标准的等级数目。

步骤2：采用集对分析的“同、异、反”思想构造评价对象的样本i子系统j指标k的单指标联系数uijk。在具体计算单指标联系数uijk时，可采用“同异反层次法”联系数表达式计算［14-15］，取G=5，单指标联系数uijk的表达式为

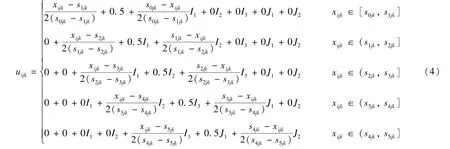
式中s0jk、s5jk分别为子系统j指标k的标准值的左极值和右极值。

步骤3：构造差异度系数的梯形模糊数。当差异度系数取值具有峰值较宽的分布特征时，可能导致基于三角模糊数的联系数存在较大误差［1，7］。陈南祥等［16］在三角模糊数的基础上，约定了相对最可能值区间［a2，a3］，其长度δ=a3-a2=0.1，构造梯形模糊数=（Imin，Iopt1，Iopt2，Imax）表示差异度系数。这种主观约定尚缺乏依据，为此，对差异度系数取值与等级标准阈值的对应关系作进一步分析。

取G=5，评价对象的子系统j指标k的等级标准阈值为一组序列数：s0jk、s1jk、s2jk、s3jk、s4jk、s5jk，采用分析取值法的特殊值法［8］确定联系分量系数取值，并建立与等级标准阈值的对应关系，如图2所示。

图2　联系分量系数取值与等级标准阈值的对应关系

由图2可见，与等级标准阈值s0jk、s1jk、s2jk、s3jk、s4jk、s5jk对应的联系分量系数为一组序列数：1、0.7、0.2、-0.2、-0.7、-1，且在［-1，1］上是连续的。此种情况下，符合2、3、4级标准的联系分量系数取值为宽值域，即存在最优取值区间［Iopt1，Iopt2］，以相邻等级标准阈值对应的联系分量系数作为该等级标准联系分量系数最小值Imin和最大值Imax，由此，可构成梯形模糊数~AI=（Imin，Iopt1，Iopt2，Imax）。如：符合2级标准的联系分量系数存在最小值Imin=-0.2，最优值区间［Iopt1，Iopt2］=［0.2，0.7］，最大值Imax=1，构造偏同差异度系数的梯形模糊数~AI1=（-0.2，0.2，0.7，1）；同理可构造中差异度系数的梯形模糊数~AI2=（-0.7，-0.2，0.2，0.7），偏反差异度系数的梯形模糊数~AI3=（-1，-0.7，-0.2，0.2）。

步骤4：确定评价指标权重，采用综合评价指标函数方法［13］计算子系统联系数uij和样本联系数ui。目前，加法加权综合方法是应用比较广泛的系统评价方法，可采用下式计算子系统联系数uij和样本联系数ui：

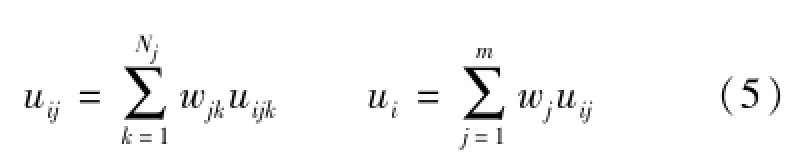
式中：wjk为子系统j指标k的指标权重；wj为子系统j的权重。

步骤5：确定置信水平α，计算联系数置信区间。根据步骤3所构造的差异度系数的梯形模糊数，由式（3）可得置信水平α下的差异度系数置信区间：

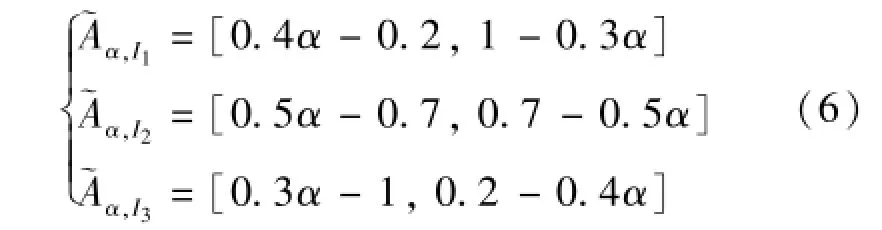
若给定置信水平α，由式（6）得差异度系数置信区间值，对立度系数取值规定为-1，由联系数表达式（式（4））计算联系数置信区间。

步骤6：根据联系数和评价等级映射关系，建立评价等级与联系数的函数计算式［14］，计算样本i子系统j指标k的单指标评价等级hijk、子系统评价等级hij和样本评价等级hi：

步骤7：综合分析。式（7）计算结果为评价等级置信区间，可采用“期望方差排序法”［4，17］对不同子区域评价等级进行优劣排序。

2　巢湖流域水资源系统脆弱性评价

巢湖流域位于安徽省中部，介于长江与淮河之间，流域总面积1.35万km2。近年来随着流域人口增长和社会经济发展，对水资源的开发利用率不断增大，污染物排放随意性较大，导致水环境污染严重，环境承载力脆弱等问题凸显。以下采用前述基于梯形模糊数联系数的评价方法对巢湖流域水资源系统脆弱性进行评价分析。

2.1巢湖流域水资源系统脆弱性评价指标体系

水资源系统脆弱性是水资源系统状态受到系统压力引起的敏感性和系统状态对系统压力的适应性的函数［4］。水资源“系统压力”往往由水资源短缺、水资源开发利用等产生，“系统状态”通常指生态环境所处的状况，而“适应性响应”可理解为系统状态在系统压力下表现出的承载能力，包括社会、经济和环境承载能力。由此，根据科学性、代表性、可操作性和动态性原则，从水资源脆弱性、生态环境脆弱性和承载能力脆弱性等三方面选择评价指标，建立巢湖流域水资源系统脆弱性评价指标体系［15］如表1所示。

2.2巢湖流域水资源系统脆弱性评价分析

根据流域水资源系统脆弱性评价指标体系，收集巢湖流域9个县市及流域指标数据，应用基于梯形模糊数联系数的评价方法对巢湖流域水资源系统脆弱性进行评价分析。

步骤1：借鉴现有水资源系统脆弱性研究成果，结合研究区域实际情况，确定巢湖流域水资源系统脆弱性评价标准，见表2。

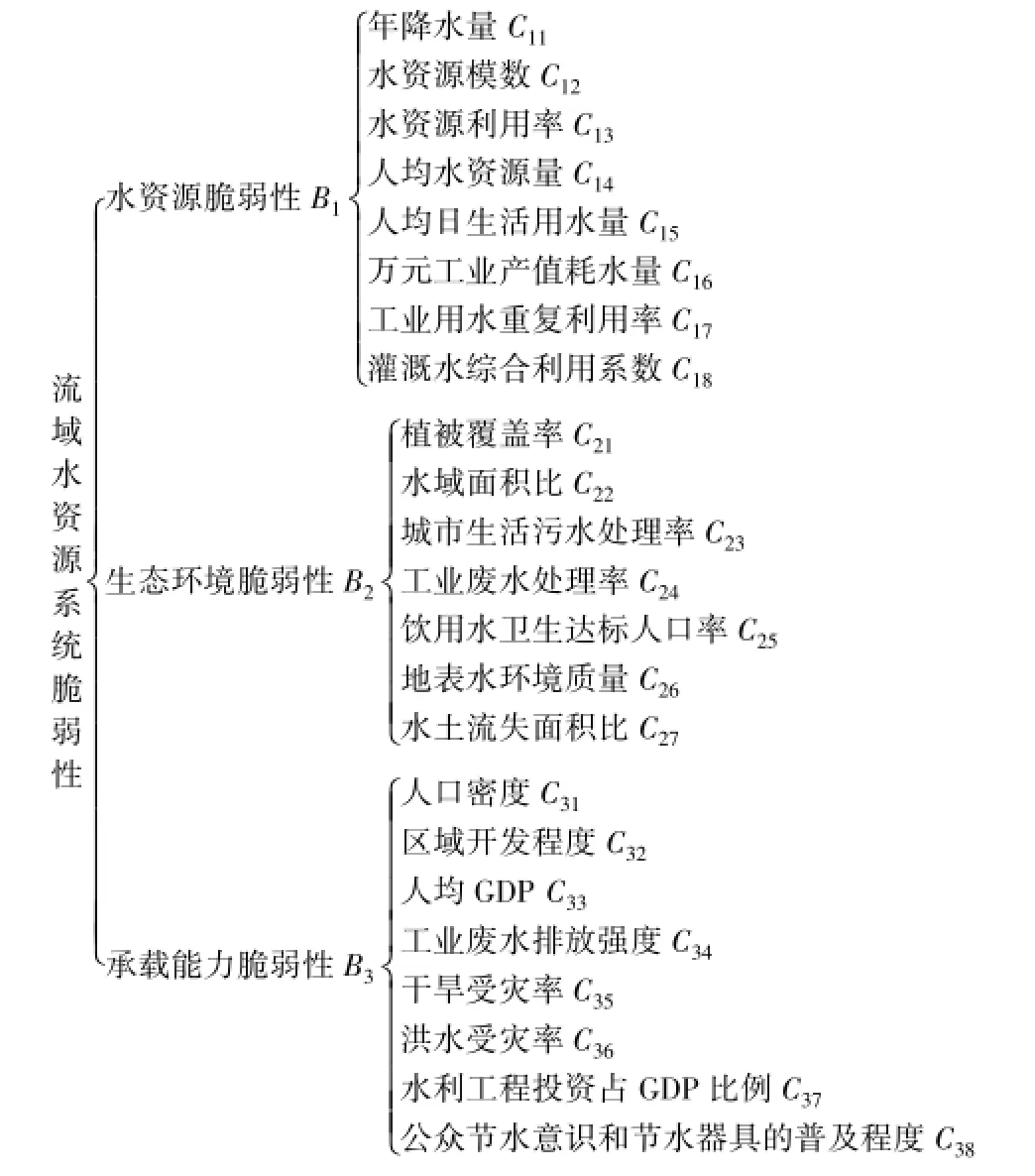
表1　巢湖流域水资源系统脆弱性评价指标体系

步骤2：采用“同异反层次法”联系数计算公式（式（4））计算巢湖流域水资源系统脆弱性评价样本i子系统j指标k的单指标联系数uijk。

步骤3：采用模糊层次分析法确定巢湖流域水资源系统脆弱性评价子系统指标权重［15］（表3），由式（5）计算得子系统联系数uij。同时分析确定3个子系统的权重为0.4、0.3和0.3，由式（5）计算得样本联系数ui，结果见表4。

步骤4：取置信水平α=75%，由式（6）可得置信水平75%条件下的差异度系数置信区间为

步骤5：由式（7）计算得巢湖流域水资源系统脆弱性等级置信区间如表4所示，表4同时给出了模糊集对分析评价方法［15］和模糊综合评价方法［18］的计算结果。

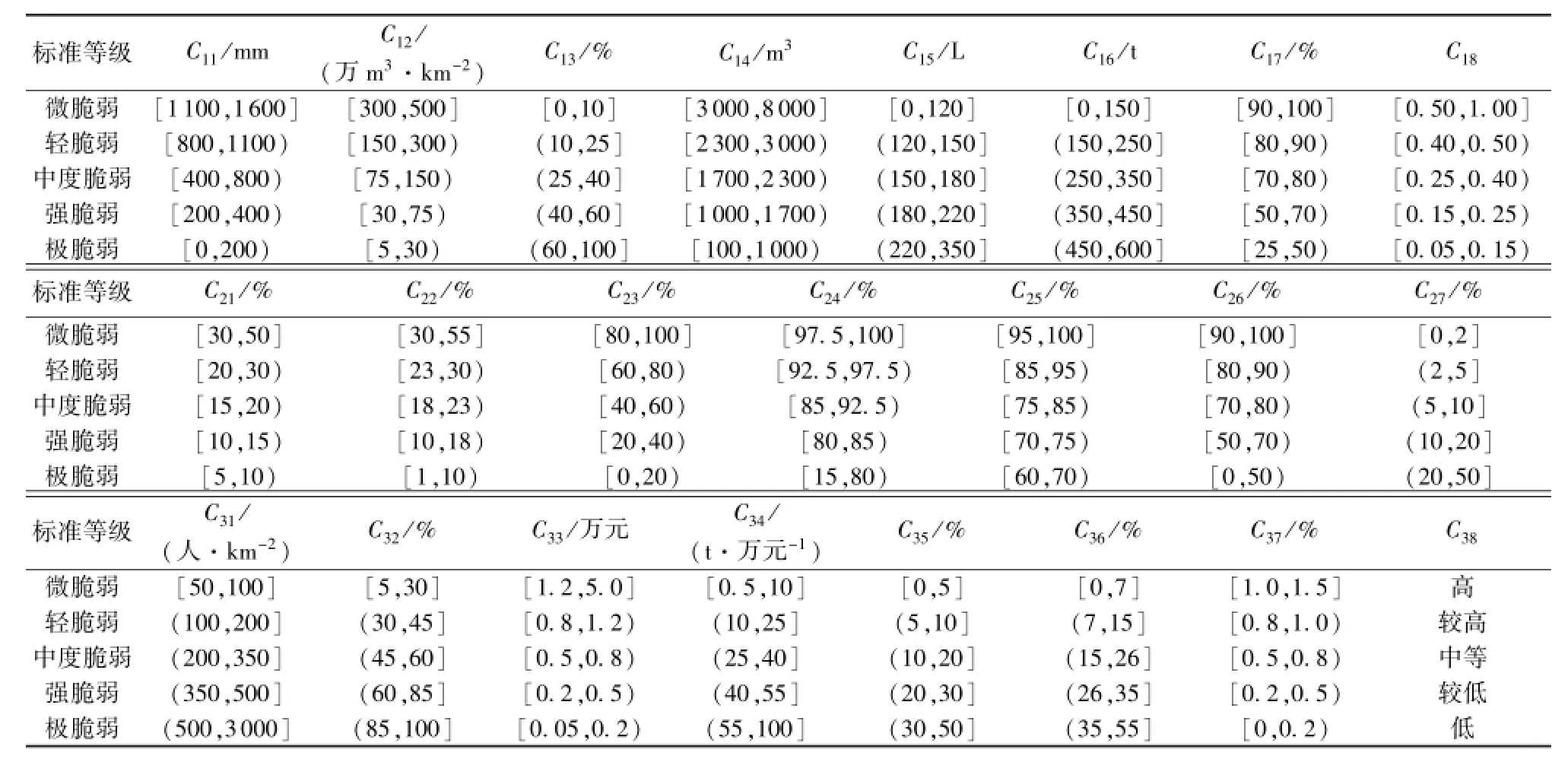
表2　巢湖流域水资源系统脆弱性评价标准

表3　巢湖流域水资源系统脆弱性评价指标权重

2.3结果分析

由表4可知，置信水平75%条件下巢湖流域水资源系统脆弱性等级区间为［2.89，3.44］，与模糊集对分析评价方法和模糊综合评价方法结果基本一致。流域不同区域的脆弱性等级优劣排序依次为肥东、和县、庐江、居巢、无为、含山、合肥、肥西和舒城。

为进一步分析巢湖流域水资源系统脆弱性的主要影响因素，表5给出了合肥、舒城和全流域的各子系统脆弱性评价结果。表5结果表明：①从子系统分析，巢湖流域水资源系统脆弱性的主要影响因素为承载能力脆弱性。随着流域人口不断增加、城镇化加快，以及水资源开发利用率的增大，造成流域范围内人口密度、区域开发程度、工业废水排放强度等指标的脆弱性状况变差，承载能力脆弱性对水资源系统脆弱性的影响逐渐增大。②合肥、舒城的生态环境脆弱性也较差，反映了随着社会经济的发展、城镇化的加快，生态环境压力逐渐加大，应加强生态环境综合治理，改善生态环境质量，降低生态环境脆弱程度。

表4　综合评价结果

表5　子系统脆弱性评价结果

3　结 语

根据差异度系数峰值取值的特征，通过分析联系分量系数取值与等级标准阈值的对应关系，确定等级标准g的联系分量系数的最优取值区间［Iopt1，Iopt2］，以相邻等级标准阈值对应的联系分量系数作为该等级标准联系分量系数最小值Imin和最大值Imax，构造了以梯形模糊数表示的差异度系数，提出了基于梯形模糊数联系数的评价方法。实例应用结果表明：基于梯形模糊数联系数的评价方法所得评价结果为置信区间，避免了当差异度系数取值峰值较宽时可能产生的误差；其中置信水平α取值采用了主观取值，如何确定置信水平的取值尚需进一步研究；对脆弱性评价等级置信区间还可采用“期望-方差排序法”对不同子区域的综合评价等级进行优劣排序，能有针对性地对脆弱性排序靠后的子区域进行综合治理，改善流域的水资源系统脆弱性状况。

［1］RONALD E G，ROBERT E Y.Analysis of the error in the standardapproximationusedformultiplicationof triangularandtrapezoidalfuzzynumbersandthe development of a new approximation［J］.Fuzzy Sets and Systems，1997，91（1）：1-13.

［2］汪哲荪，金菊良，魏一鸣，等.三角模糊数随机模拟的防洪工程联系数风险评价模型［J］.水利学报，2010，41（10）：1173-1178.（WANG Zhesun，JIN Juliang，WEI Yiming，et al.Connection number based risk evaluation method for watershed flood control engineering system using stochastic simulation and triangular fuzzy numbers［J］.Journal of Hydraulic Engineering，2010，41（10）：1173-1178.（in Chinese））

［3］潘争伟，吴开亚，金菊良，等.三角模糊数的联系数在环境质量评价中的应用［J］.安阳工学院学报，2009（2）：39-43.（PAN Zhengwei，WU Kaiya，JIN Juliang，et al.The connection number based on the triangular fuzzy number and its application to urban evaluation of environmental quality［J］.Journal of Anyang Institute of Technology，2009（2）：39-43.（in Chinese））

［4］潘争伟，金菊良，吴开亚，等.区域水环境系统脆弱性指标体系及综合决策模型研究［J］.长江流域资源与环境，2014，23（4）：518-525.（PAN Zhengwei，JIN Juliang，WU Kaiya，et al.Research on the indexes and decision methodofregionalwaterenvironmentalsystem vulnerability［J］.Resources and Environment in the Yangtze Basin，2014，23（4）：518-525.（in Chinese））

［5］杨淇翔，陈南祥.基于集对分析与三角模糊数耦合的地下水环境质量评价［J］.中国农村水利水电，2012（8）：38-42.（YANG Qixiang，CHEN Nanxiang.A coupling model of set pair analysis and triangular fuzzy numbers for evaluation of groundwater environmental quality［J］.China Rural Water and Hydropower，2012（8）：38-42.（in Chinese））

［6］彭涛，陈晓宏，王高旭，等.基于集对分析与三角模糊数的滨海湿地生态系统健康评价［J］.生态环境学报，2014，23（6）：917-922.（PENG Tao，CHEN Xiaohong，WANG Gaoxu，et al.Assessment of coastal wetland ecosystem health based on set pair analysis and triangular fuzzy numbers［J］.Ecology and Environmental Sciences，2014，23（6）：917-922.（in Chinese））

［7］李如忠，童芳，周爱佳，等.基于梯形模糊数的地表灰尘重金属污染健康风险评价模型［J］.环境科学学报，2011，31（8）：1790-1798.（LI Ruzhong，TONG Fang，ZHOU Aijia，et al.Fuzzy assessment model for the health risk of heavy metals in urban dusts based on trapezoidal fuzzy numbers［J］.Acta Scientiae Circumstantiae，2011，31（8）：1790-1798.（in Chinese））

［8］赵克勤.集对分析及其初步应用［M］.杭州：浙江科学技术出版社，2000：9-43.

［9］刘颖，于冬梅，程显毅.联系数学中的几个问题［J］.数学的实践与认识，2004，34（10）：77-82.（LIU Ying，YU Dongmei，CHENG Xianyi.Several questions in connection mathematics［J］.Mathematics in Practice and Theory，2004，34（10）：77-82.（in Chinese））

［10］赵克勤.SPA的同异反系统理论在人工智能研究中的应用［J］.智能系统学报，2007，2（5）：20-35.（ZHAO Keqin.TheapplicationofSPA-basedidenticaldiscrepancy-contrary system theory in artificial intelligence research［J］.CAAI Transactions on Intelligent Systems，2007，2（5）：20-35.（in Chinese））

［11］杨纶标，高英仪，凌卫新.模糊数学原理及应用［M］.广州：华南理工大学出版社，2011：1-30.

［12］曾文艺，罗承忠，肉孜阿吉.区间数的综合决策模型［J］.系统工程理论与实践，1997（11）：48-50.（ZENG Wenyi，LUOChengzhong，ROZIHaji.Comprehensive decisionmodelofintervalnumber［J］.Systems Engineering Theory&Practice，1997（11）：48-50.（in Chinese））

［13］金菊良，魏一鸣.复杂系统广义智能评价方法与应用［M］.北京：科学出版社，2008：26-29.

［14］吴开亚，金菊良，潘争伟.基于三角模糊数截集的联系数模型在城市涝灾影响等级评价中的应用［J］.水利学报，2010，41（6）：711-719.（WU Kaiya，JIN Juliang，PAN Zhengwei.Set pair analysis model based on triangle fuzzy intervals and its application to impact rating evaluation of urban flood［J］.Journal of Hydraulic Engineering，2010，41（6）：711-719.（in Chinese））

［15］胡蓓琳，潘争伟，金菊良，等.基于集对分析模型的巢湖流域水资源系统脆弱性评价［J］.水电能源科学，2013，31（10）：21-24.（HU Beilin，PAN Zhengwei，JIN Juliang，et al.Vulnerability evaluation of Chaohu Basin water resources system based on set pair analysis method［J］. Water Resources and Power，2013，31（10）：21-24.（in Chinese））

［16］陈南祥，杨淇翔.基于博弈论组合赋权的流域水资源承载力集对分析［J］.灌溉排水学报，2013，32（2）：81-85.（CHEN Nanxiang，YANG Qixiang.Set pair analysis of watershed water resources carrying capacity based on game theory combination weighting［J］.Journal of Irrigation and Drainage，2013，32（2）：81-85.（in Chinese））

［17］吴超，胡昆.区间数多属性决策中权重灵敏度分析［J］.系统工程与电子技术，2004，26（9）：1217-1218.（WU Chao，HU Kun.Sensitivity analysis to weight of priorities in multiple attribute decision making with intervals［J］. Systems Engineering and Electronics，2004，26（9）：1217-1218.（in Chinese））

［18］王文圣，张翔，金菊良，等.水文学不确定性分析方法［M］.北京：科学出版社，2011：188-202.

Assessment method using connection number based on trapezoidal fuzzy numbers and its application

PAN Zhengwei1，2，JIN Juliang3，4，ZHOU Rongxing1
（1.School of Civil Engineering and Environmental Engineering，Anhui Xinhua University，Hefei 230088，China；2.Institute of Safety and Environmental Assessment，Anhui Xinhua University，Hefei 230088，China；3.School of Civil Engineering，Hefei University of Technology，Hefei 230009，China；4.Institute of Water Resources and Environmental Systems Engineering，Hefei University of Technology，Hefei 230009，China）

Using a triangular fuzzy number to express the difference degree coefficient might lead to a large error when the connection components show a broad peak distribution characteristic.The optimal interval of the difference degree coefficient was determined，the difference degree coefficient was formulated with the trapezoidal fuzzy numbers，and an assessment method using the connection number based on trapezoidal fuzzy numbers was developed through analysis of the relationship between the difference degree coefficient and grade standard threshold.The method was applied to vulnerability assessment of the water resources system in the Chaohu Basin.The results show that the confidence interval of the vulnerability grade in the water resources system in the Chaohu Basin is［2.89，3.44］with a 75%confidence level.This method can not only obtain the confidence interval of the evaluation grade and effectively avoid the error induced by the broad peak of the difference degree coefficient，but also determine the priorities of vulnerability grades in different subregions using the expectation-variance method

connection number；trapezoidal fuzzy number；water resources system；vulnerability assessment；Chaohu Basin

TV213.4；P964

A

10067647（2016）05006906

10.3880/j.issn.10067647.2016.05.013

国家自然科学基金（51309004，71273081）；安徽高校自然科学研究重点项目（KJ2016A302）

潘争伟（1980—），男，副教授，硕士，主要从事环境与资源系统工程研究。E-mail：pzhwei1023@163.com

（20150811 编辑：熊水斌）