天然产物的绝对构型研究（Ⅱ）通过比较旋光和碳氢谱的实验值与计算值确定生物碱类化合物的绝对构型

胡栋宝，周北斗2

（1.玉溪师范学院资源环境学院，玉溪653100；2.莆田学院药学与医学技术学院，莆田351100）

天然产物的绝对构型研究（Ⅱ）通过比较旋光和碳氢谱的实验值与计算值确定生物碱类化合物的绝对构型

胡栋宝1，周北斗2

（1.玉溪师范学院资源环境学院，玉溪653100；2.莆田学院药学与医学技术学院，莆田351100）

在研究天然产物绝对构型的过程中，筛选了一些绝对构型未确定的生物碱类化合物，利用密度泛函理论（DFT）在不同的计算水平下得出其旋光和碳氢谱数据.理论值与实测值对比分析结果表明，二者基本符合，从而鉴定出这些化合物的绝对构型.

天然产物；生物碱；密度泛函理论（DFT）；旋光；绝对构型

天然产物绝对构型（AC）的鉴定在有机化学研究中占有十分重要的地位.目前，许多已经报道的天然产物的绝对构型并未被鉴定，系统鉴定这些化合物的绝对构型对于合成这些化合物具有重要意义.近年来，计算化学被广泛应用于鉴定或纠正天然产物手性分子的绝对构型［1～12］，运用密度泛函理论（DFT）计算旋光（OR）、电子圆二色光谱（ECD）、振动圆二色光谱（VCD）数据并与实验数值作对比来确定天然产物绝对构型的研究日益受到科研工作者的重视［13～25］.作为系列的理论研究工作之一，本文通过计算旋光和碳氢谱数据确定了所选择的7个天然产物生物碱的绝对构型，并且初步探讨了不同计算水平对旋光数值的影响.

1 计算方法

首先，运用Spartan06构象搜索软件在MMFF分子力场对所选择的7个生物碱化合物（1～7，结构见图1）［28～33］进行构象搜索；然后，对所有搜索到的构象都在气相条件下采用B3LYP方法进行能量优

化，从而找到能量差在0～10 kJ／mol范围内的稳定构象（与最低能量构象相比）.对于被挑选出来的构象，分别在气相和溶液2种条件下计算其旋光值，为了模拟真实旋光测定条件，在研究溶液条件下的旋光时，采用连续极化模型PCM［26］.在计算旋光值时，采用的基组由具体情况确定.为了证实所研究分子相对构型的正确性，采用DFT／GIAO方法和6⁃311＋G（2d，p）基组，对其进行碳氢谱的计算.为了便于与实验值作比较，以589.3 nm（钠D线）作为旋光计算的波长.所有计算均采用Gaussian 03软件包［27］.

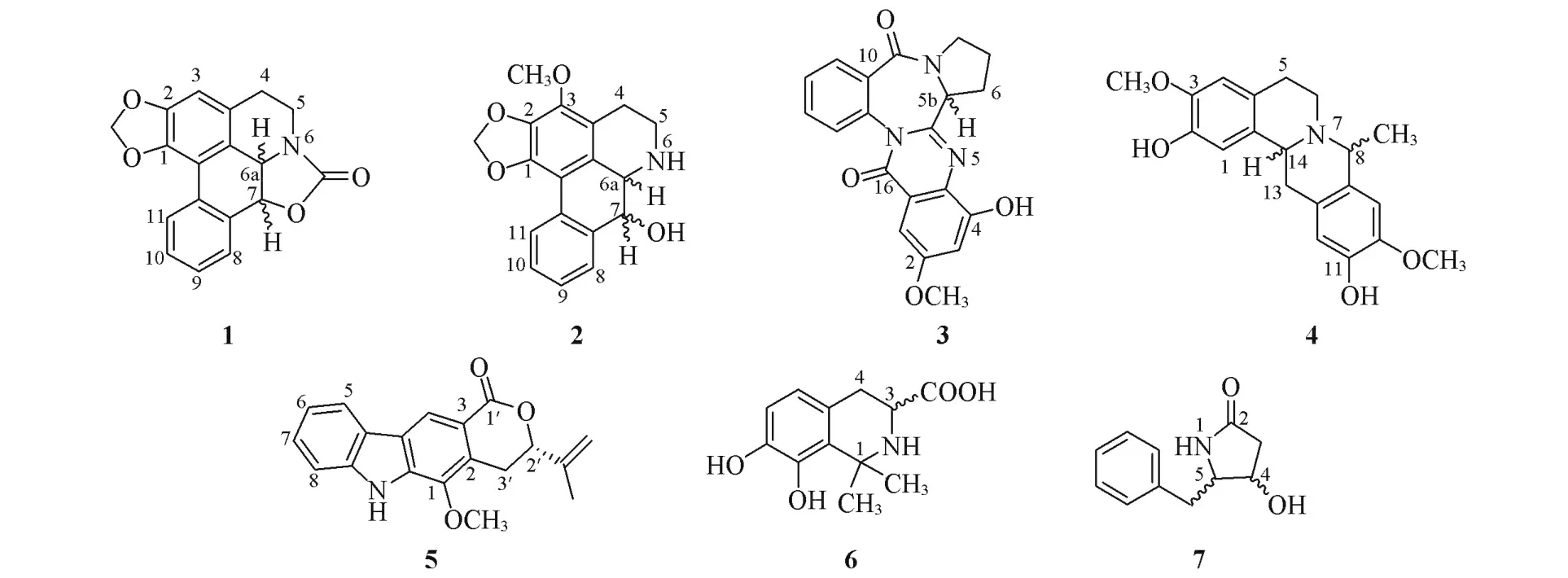
Fig.1 Structures of compounds 1—7

2 结果与讨论

在所选择的化合物1～7中，除化合物5外，其余6个化合物均未通过实验确定绝对构型.化合物5的绝对构型鉴定通过测定其电子圆二色光谱（ECD）并与已知化合物的谱图比较推断得出［31］，为了验证ECD解决此类天然产物绝对构型的可靠性，计算了化合物5的旋光和碳谱数据，以期对其绝对构型进行验证.化合物5因其旋转自由度而形成4个不同能量的构象（图2），对其每个构象的旋光值均进行计算，然后采用Boltzmann统计公式计算该分子的总旋光值，进而与实验值作比较.由表1和图3可知，化合物5在气相中的旋光计算值为＋48.2°［B3LYP／6⁃311＋＋G（2d，p）／／B3LYP／6⁃311＋＋G（2d，p）水平］，而文献值［31］为＋52°（甲醇溶液中测试），可见计算值与实验值基本吻合；当使用PCM甲醇模型进行溶剂条件下的模拟计算时，旋光符号不变，但是数值从＋48.2°减小到＋20.4°，说明对于生物碱5这种具有柔性结构的化合物，连续极化溶剂模型PCM并未有效地提高其计算精度.但是，无论在气相还是溶液条件下计算得到的旋光符号均与实验值一致，从而可确定化合物5的2′位置为S构型，进一步说明实验采用ECD方法来鉴定化合物5的绝对构型是可靠的.Polavarapu［34］曾指出，在鉴定有机化合物绝对构型时，采用不止一种绝对构型的鉴定方法将在很大程度上提高鉴定的准确性.因此，对于生

物碱5从旋光计算的角度进一步验证了其绝对构型的可靠性.另外，Kwit等［35］在对具有多个旋转自由度的柔性分子（构象较多）进行旋光计算时发现，小基组优化后的分子构象采用高水平方法进行旋光计算有时会得出错误的结论，最好使用大基组优化，然后在大基组条件下计算旋光，这样可以显著减少计算的错误率.这在本研究中得到了进一步的证实.生物碱6也是柔性分子，具有3个稳定构象，采用与生物碱5相同的方法对其进行了旋光计算，计算值与实验值（甲醇溶液中测试）差别不大，从而确定其3位手性碳原子为S构型.为了验证化合物5的另外一种异构体（2′R）⁃5旋光计算值与实验值的吻合度，对其在B3LYP／6⁃31G（d）水平下进行了旋光计算，得计算值为－45.5°，与实验值符号相反，基于以上分析，可以得出生物碱5中手性碳原子的绝对构型应为2′S；同样，为了验证化合物6存在的另外可能构型3R，采用与化合物5相同的方法对（3R）⁃6进行旋光计算，得计算值为＋85°，与实验值符号相反，从而说明生物碱6手性碳原子的绝对构型应为3S.

Fig.2 Optim ized structures and themost stable conformers of com pounds 1—7

Table 1 Calculated，experimental optical rotations（ORs）for compounds 1—7 at the different levels

Fig.3 Real configuration of com pounds 1—7

化合物1与2是从中国台湾南部的一种植物A．uncinatus的果实中提取分离到的2个生物碱［28］，其相对构型已经由NMR确定，但是绝对构型还未被确定.在实验中，通过核磁共振谱的藕合常数可判断化合物1中的6a⁃H与7⁃H处于相反的位置关系，而在化合物2中6a⁃H与7⁃H处于同侧的位置关系，因为其相对构型已经确定，可以通过计算旋光值的方法来确定其绝对构型.对于化合物1，对其2个手性中心按6a S，7S构型，分别在4种不同水平计算其旋光值.当采用PCM模型（氯仿作溶剂）进行旋光计算时，计算值为－96.72°，与实验值－102.7°（氯仿中测定）接近，说明对于化合物1这种只有1个稳定构象的刚性分子，PCM模拟真实环境条件能够有效地提高旋光计算的精度，这与前面提到的柔性分子生物碱5和6情况不同，说明PCM溶剂模型对于构象较多的柔性分子极其敏感，当分子旋转

自由度较多时，分子在构象互变时，PCM模型不能有效描述溶质与溶剂之间的相互作用力问题，如分子内氢键作用、分子间氢键、极性溶剂与溶质之间作用力等问题.计算结果表明，PCM溶剂模型对于刚性分子效果较好，但对于柔性分子而言精度较差.对于化合物2，无论是否采用PCM模型（氯仿作溶剂），旋光计算值与实验值均较接近，在气相中约为－230°，采用PCM模型后接近－180°，而实验值为－121.5°（氯仿中测定），理论计算值与实验值较吻合.为了验证化合物1的另外一种异构体（6a R，7R）⁃1与实验值的吻合度，对其在B3LYP／6⁃31G（d）水平下进行了旋光计算，计算值为＋136°，与实验旋光值符号相反；对于可能存在的另外2种异构体（6a R，7S）⁃1和（6a S，7R）⁃1，在同样水平下也进行了旋光计算，计算值分别为＋110°和－60°，2个计算结果均与其实验值存在较大差异.基于以上分析，可以推断生物碱1的2个手性碳原子的绝对构型应为6a S，7S.同样，为了验证化合物2存在的可能构型（6a R，7S）⁃2，采用与化合物1相同的方法进行了旋光计算，计算值为＋230°，与实验值符号也相反；对可能存在的另外2种异构体（6a S，7S）⁃2和（6a R，7R）⁃2，在同样水平下进行了旋光计算，计算值分别为＋190°和－280°，2个计算值均与实验值存在较大差异，所以推断生物碱2的2个手性碳原子的绝对构型应为6a S，7R.

化合物3和4也是从天然产物中得到的生物碱［29，30］，通过NMR已经确定了手性碳上氢原子的相对构型，但其绝对构型未确定.这2个化合物的分子结构中都具有2个旋转自由度—OH和—OCH3，通过构象搜索，发现其都有2个稳定构象，应该属于半刚性分子，采用2种不同的方法对其旋光值进行计算（表1）.对于生物碱3，在气相中的计算旋光值为－135.0°，采用PCM极化模型（甲醇溶剂模型）后的计算旋光值为－94.4°，而其实验值为－90°（甲醇溶液中测试）.此结果表明，对于像化合物3这样只有2个稳定构象的半刚性分子，采用PCM连续极化模型能有效提高旋光的计算准确性.对于生物碱分子4，在气相中的计算旋光值为＋152.5°，而采用PCM模型后计算旋光值为＋98.6°，而实验值为＋198°（甲醇溶液中测试），虽然符号不变，但采用PCM模型后的数值偏离实验值较大，这有可能是由于化合物4形成了分子内氢键所致，因为其—OH与—OCH3处于邻位，易形成分子内氢键，因而增大了计算旋光值与实验旋光值大小的差异.尽管如此，这并不妨碍对其绝对构型的判断.为了验证化合物3可能存在的另外一种异构体（5b R）⁃3与实验值的吻合度，对（5b R）⁃3在B3LYP／6⁃31G（d）水平下进行了旋光计算，计算值为＋125.0°，与实验值符号相反.基于此可以推断生物碱3中手性碳原子的绝对构型应为5b S.同样，为了验证化合物4可能存在的异构体（8R，14S）⁃4，采用与化合物1相同的方法进行了旋光计算，计算值为－132.5°，与实验值符号相反；对可能存在的另外2种异构体（8R，14R）⁃4和（8S，14S）⁃4也采用相同方法进行了旋光计算，计算值分别为＋75°和－160.5°，2个计算值均与实验值存在较大差异.基于以上分析，推断出生物碱3手性中心C5b的绝对构型为S，生物碱4的手性碳原子绝对构型为8S，14R.

生物碱7是从深海生物中提取分离到的具有显著生物活性的化合物［33］，该分子的绝对构型未被确定.在实验上，该化合物的相对构型是通过ROESY谱鉴定的，结果表明C4与C5上面的氢原子处于五元环同侧，但是其绝对构型不能确定.困难的是该生物碱分子的实验旋光值只有－12°（甲醇溶液中测试），而且为柔性分子.研究表明，一个天然产物的旋光数值很大，即使用小基组优化构象分子，通常旋光符号也不会变化，若实验旋光值较小，则需考虑用大基组优化，尤其对于柔性分子（构象多）［19，35］.为了鉴定出该分子的绝对构型，采用6种不同的方法计算其旋光值（表1）.由此可知，无论采用小基组优化高水平旋光计算，或在高水平条件下优化再用高水平方法计算，旋光符号始终与实验值一致，数值的差异可能是实验过程中手性拆分不完全或者实验条件比如温度、溶剂效应和溶液浓度等原因造成的.尽管存在数值差异，但从旋光符号进行定性分析，其2个手性中心的绝对构型应该为4S，5S.为了验证化合物7存在的另外一种异构体（4R，5R）⁃7与实验的吻合度，对其在B3LYP／6⁃31G（d）水平下进行了旋光计算，得计算值为＋30°，与实验值符号相反.基于以上分析，可以推断生物碱7中2个手性碳原子的绝对构型应该是4S，5S.

为了检验上述7个生物碱分子的平面相对构型，参照文献［36～46］方法，采用GIAO法在B3LYP／6⁃311＋G（2d，p）水平进行了以上分子的碳谱或者氢谱的计算，将计算所得结果与实验值进行比较发现，

化合物1～7均具有较小的化学位移相对误差，从而保证了其分子平面相对构型的准确性（表S1～S7，见本文支持信息）.

3 结 论

运用密度泛函理论（DFT）计算确定了7个天然产物生物碱分子的旋光值，并与实验结果进行比较，讨论了不同计算水平下不同计算方法的优缺点：对于构象较少的生物碱分子，溶剂模型PCM可以有效提高其旋光计算结果的精度，而对于构象较多的生物碱分子却不能有效提高其计算精度.该研究结果为今后该类分子立体手性中心的确定提供了方法学上的参考.

支持信息见http：／／www.cjcu.jlu.edu.cn／CN／10.7503／cjcu20160228.

［1］ Ren J.，Zhu H.J.，Chem．J．Chinese Universities，2009，30（10），1907—1918（任洁，朱华结.高等学校化学学报，2009，30（10），1907—1918）

［2］ Shen L.，Zhao S.D.，Zhu H.J.，Chem．J．Chinese Universities，2011，32（11），2568—2573（沈岚，赵声定，朱华结.高等学校化学学报，2011，32（11），2568—2573）

［3］ Zhu H.J.，Liu L.，Yang Q.，Chem．J．Chinese Universities，2015，36（8），1559—1562（朱华结，刘莉，杨芹.高等学校化学学报，2015，36（8），1559—1562）

［4］ Niu Z.G.，Li D.C.，Liu D.，Xia D.，Zou Y.，Sun W.，Li G.N.，Chem．Res．Chinese Universities，2014，30（3），425—430

［5］ Liu T.T.，Lu X.，Zhang M.T.，Chem．Res．Chinese Universities，2014，30（4），656—660

［6］ Liao T.G.，Ren J.，Fan H.F.，Xie M.，Zhu H.J.，Tetrahedron：Asymmetry，2008，19（7），808—815

［7］ Liu D.Z.，Wang F.，Liao T.G.，Tang J.G.，Steglich W.，Zhu H.J.，Liu J.K.，Org．Lett．，2006，8（25），5749—5752

［8］ Crawford T.D.，Owens L.S.，Tam M.C.，Schreiner P.R.，Koch H.，J．Am．Chem．Soc．，2005，127（1），1368—1369

［9］ Giorgio E.，Minichino C.，Viglione R.G.，Zanasi R.，Rosini C.，J．Org．Chem．，2003，68（13），5186—5192

［10］ Mennucci B.，Claps M.，Evidente A.，Rosini C.，J．Org．Chem．，2007，72（18），6680—6691

［11］ Miguel R.N.，Sastre J.A.L.，Galisteo D.，Martin A.D.，Ramos A.G.，J．Mol．Struc．，2000，522（1），219—231

［12］ Stephens P.J.，Pan J.J.，Devlin F.J.，Cheeseman J.R.，J．Nat．Prod.，2008，71（2），285—288

［13］ Crawford T.D.，Theor．Chem．Acc.，2006，115（4），227—245

［14］ Hu D.B.，Zhang S.，He J.B.，Dong Z.J.，Li Z.H.，Liu J.K.，Fitoterapia，2015，104，50—54

［15］ Stephens P.J.，McCann D.M.，Devlin F.J.，Flood T.C.，Butkus E.，Stoncius S.，Cheeseman J.R.，J．Org．Chem．，2005，70（10），3903—3913

［16］ Gomez⁃Hurtado M.A.，Torres⁃Valencia J.M.，Manríquez⁃Torres J.，Río R.E.D.，Motilva V.，García⁃Mauriño S.，Avila J.，Talero E.，Cerda⁃García⁃Rojas C.M.，Joseph⁃Nathan P.，Phytochemistry，2011，72（4），409—414

［17］ Stephens P.J.，Pan J.J.，Devlin F.J.，J．Org．Chem．，2007，72（9），3521—3536

［18］ Devlin F.J.，Stephens P.J.，Scafato P.，Superchi S.，Rosini C.，Tetrahedron：Asymmetry，2001，12（11），1551—1558

［19］ Giorgio E.，Roje M.，Tanaka K.，Hamersak Z.，J．Org．Chem．，2005，70（17），6557—6563

［20］ Tam M.C.，Crawford T.D.，J．Phys．Chem．A，2006，110（6），2290—2298

［21］ Lattanzi A.，Scettri A.，Zanasi R.，J．Org．Chem．，2010，75（7），2179—2188

［22］ Stephens P.J.，Denlin F.J.，Cheeseman J.R.，Frish M.J.，J．Phys．Chem．A，2001，105（22），5356—5357

［23］ Wiberg K.B.，Wang Y.G.，Wilson S.M.，Vaccaro P.H.，Jorgensen W.L.，Crawford T.D.，Abrams M.L.，Cheeseman J.R.，Luderer M.，J．Phys．Chem．A，2008，112（11），2415—2422

［24］ Wiberg K.B.，Wang Y.G.，Wilson S.M.，Vaccaro P.H.，Cheeseman J.R.，J．Phys．Chem．A，2005，109（15），3448—3453

［25］ Ren J.，Jiang J.X.，Li L.B.，Liao T.G.，Tian R.R.，Chen X.L.，Jiang S.P.，Jr.C.U.P.，Zhu H.J.，Eur．J．Org．Chem.，2009，2009（23），3987—3991

［26］ MiertušS.，Scrocco E.，Tomasi J.，Chem．Phys．，1981，55（1），117—129

［27］ Frisch M.J.，Trucks G.W.，Schlegel H.B.，Scuseria G.E.，Robb M.A.，Cheeseman J.R.，Montgomery Jr.J.A.，Vreven T.，Kudin K.N.，Burant J.C.，Millam J.M.，Iyengar S.S.，Tomasi J.，Barone V.，Mennucci B.，CossiM.，ScalmaniG.，Rega N.，Petersson G. A.，Nakatsuji H.，Hada M.，Ehara M.，Toyota K.，Fukuda R.，Hasegawa J.，Ishida M.，Nakajima T.，Honda Y.，Kitao O.，Nakai H.，Klene M.，LiX.，Knox J.E.，Hratchian H.P.，Cross J.B.，Adamo C.，Jaramillo J.，Gomperts R.，Stratemann R.E.，Yazyev O.，Austin A.J.，Cammi R.，Pomelli C.，Ochterski J.W.，Ayala P.Y.，Morokuma K.，Voth G.A.，Salvador P.，Dannenberg J.J.，Zakrzewski V.

G.，Dapprich S.，Daniels A.D.，Strain M.C.，Farkas O.，Malick D.K.，Rabuk A.D.，Raghavachari K.，Foresman J.B.，Ortiz J.V.，Cui Q.，Baboul A.G.，Clifford S.，Cioslowski J.，Stefanov B.B.，Liu G.，Liashenko A.，Piskorz P.，Komaromi I.，Martin R.L.，Fox D. J.，Keith T.，Al⁃Laham M.A.，Peng C.Y.，Nanayakkara A.，Challacombe M.，Gill P.M.W.，Johnson B.，Chen W.，Wong M.W.，Gonzalez C.，Pople J.A.，Gaussian 03 User's Reference，Gaussian Inc.，Carnegie PA，2003

［28］ Hsieh T.J.，Chen C.Y.，Kuo R.Y.，Chang F.R.，Wu Y.C.，J．Nat．Prod．，1999，62（8），1192—1193

［29］ Rahbaek L.，Breinholt J.，J．Nat．Prod．，1999，62（6），904—905

［30］ Amaral A.C.F.，Barnes R.A.，Phytochemistry，1998，47（7），1445—1447

［31］ Shen D.Y.，Chao C.H.，Chan H.H.，Huang G.J.，Hwang T.L.，Lai C.Y.，Lee K.H.，Thang T.D.，Wu T.S.，Phytochemistry，2012，82（1），110—117

［32］ Misra L.，Wagner H.，Phytochemistry，2004，65（18），2565—2567

［33］ Shin H.J.，Kim T.S.，Lee H.S.，Park J.Y.，Choi I.K.，Kwon H.J.，Phytochemistry，2008，69（12），2363—2366

［34］ Polavarapu P.L.，Chirality，2008，20（5），664—672

［35］ Kwit M.，Rozwadowska M.D.，Gawronski J.，Grajewska A.，J．Org．Chem.，2009，74（21），8051—8063

［36］ Barone G.，Gomez⁃Paloma L.，Duca D.，Silvestri A.，Riccio R.，Bifulco G.，Chem．Eur．J．，2002，8（14），3233—3239

［37］ Betz J.，BauerW.，J．Am．Chem．Soc．，2002，124（29），8699—8706

［38］ Bifulco G.，Bassarello C.，Riccio R.，Gomez⁃Paloma L.，Org．Lett．，2004，6（6），1025—1028

［39］ Monica C.D.，Randazzo A.，Bifulco G.，Cimino P.，Aquino M.，Izzo I.，Riccardis F.D.，Gomez⁃Paloma L.，Tetrahedron Lett．，2002，43（33），5707—5710

［40］ Fattorusso C.，Stendardo E.，Appendino G.，Fattorusso E.，Luciano P.，Romano A.，Taglialatela⁃Scafatis O.，Org．Lett.，2007，9（12），2377—2380

［41］ Forsyth D.A.，Tilley L.J.，Prevoir S.J.，J．Chem．Edu．，2002，79（5），593—600

［42］ Helgaker T.，JaszunskiM.，Ruud K.，Chem．Rev．，1999，99（1），293—352

［43］ Rychnovsky S.，Org．Lett．，2006，8（13），2895—2898

［44］ Sebag A.，Forsyth D.A.，Plante M.，J．Org．Chem．，2001，66（24），7967—7973

［45］ Wipf P.，Kerekes A.D.，J．Nat．Prod．，2003，66（5），716—718

［46］ Steven G.S.，Robert S.P.，Jonathan W.B.，Jonathan M.G.，J．Org．Chem．，2008，73（11），4053—4062

Absolute Configuration Determ ination for Natural Products（Ⅱ）†Absolute Configuration Determ ination for Alkaloids by Comparing Computed Optical Rotations，13C NMR and1H NMR with the Experimental Results

HU Dongbao1，ZHOU Beidou2∗
（1．School ofResource and Environment，Yuxi Normal University，Yuxi653100，China；2．School of Pharmacy and Medical Technology，Putian University，Putian 351100，China）

In order to study the absolute configuration of natural product，some compounds of undetermined absolute configuration were screened，the optical rotation（OR），13C NMR and1H NMR data were gotten by density functional theory（DFT）at different computational levels.The computational results matched the experimental resultswell.The results show that the PCM solventmodel could improve the accuracy of compu⁃ted optical rotation for the rigid alkaloid molecules but not be applicable to flexible ones.Therefore，the chira⁃lity centers of these alkaloidswere determined.

Natural product；Alkaloid；Density functional theory；Optical rotation；Absolute configuration

O629.9

A

10.7503／cjcu20160228

（Ed.：P，H，D，K）

†Supported by the Education Scientific Research Project for Middle⁃age and Young Teachers of Fujian Province，China（No.JA15453），the Project of Education Departmentof Yunnan Province，China（No.2016ZZX200），the Science and Technology Planning Projectof Putian City，Chi⁃na［No.2014S02（3）］and the Research Projects of Putian University，China（Nos.2014053，2015076）.

2016⁃04⁃11.

日期：2016⁃10⁃19.

福建省中青年教师教育科研项目（批准号：JA15453）、云南省教育厅项目（批准号：2016ZZX200）、莆田市科技计划项目［批准号：2014S02（3）］和莆田学院科研项目（批准号：2014053，2015076）资助.

联系人简介：周北斗，男，博士，讲师，主要从事天然有机化学与计算化学研究.E⁃mail：zhoubeidou@mail.kib.ac.cn