基于有限质点法的输电导线微风振动研究
2016-11-23谢文平徐宁波罗啸宇李黎
谢文平,徐宁波,罗啸宇,李黎
(1.广东电网有限责任公司电力科学研究院,广东 广州 510080;2.华中科技大学 土木工程与力学学院,湖北 武汉 430074)
基于有限质点法的输电导线微风振动研究
谢文平1,徐宁波2,罗啸宇1,李黎2
(1.广东电网有限责任公司电力科学研究院,广东 广州 510080;2.华中科技大学 土木工程与力学学院,湖北 武汉 430074)
特高压输电线路导线微风振动对线路的破坏日趋明显,基于此,采用有限质点法对导线的微风振动响应进行研究。通过采用构件的点值描述,将构件离散为质点,质点与质点之间通过单元连接,质点的运动遵循牛顿第二定律,并通过中心差分法求解质点的运动来追踪构件的行为。计算发现,有限质点法能考虑输电线质量、几何非线性的影响,计算结果更加真实。最后,采用有限质点法计算了不同风激励条件下导线微风振动的响应,且计算分析结果与能量平衡法的结果基本吻合,表明有限质点法的正确性。
微风振动; 能量平衡法; 有限质点法; 向量式构件力学
特高压输电线路拥有高效率、远距离、大容量等优点,在优化我国电力资源配置上起到举足轻重的作用,同时,在提高国民经济效益以及促进开发清洁能源等方面均具有重要意义。长期以来,输电导线微风振动都是一个比较关心的问题,随着导线运行张力的增大,微风振动发生的更为频繁,由此导致的金具磨损、导线疲劳断线事故屡有发生,因此,研究输电导线微风振动分析具有较强的现实意义[1-8]。
导线的微风振动又称为涡激振动,当风速较小的横向风(一般为0.5~10.0 m/s)吹过导线时,会在其背后产生稳定脱落的卡门漩涡[9],在输电线上引起交替变化的作用力,使其产生垂直振动,振动频率在3~150 Hz之间,振幅一般不超过导线直径的1~2倍。相比于导线的次档距振荡和舞动,其微风振动发生的更为频繁,研究导线微风振动响应成为输电线力学重要的分支。目前,国内外有不少学者都对导线的微风振动响应进行了计算分析。J.Vecchiarelli[10]等采用有限差分法对导线进行了微风振动响应计算,并将结果与能量平衡法进行了对比,李黎[11-12]等分别利用改进的能量平衡法和有限元法计算了导线的微风振动响应,并对其影响因素进行了分析。
以上学者对导线微风振动响应计算都做了较充分的研究,并且也能得到较精确的解,但仍有一些没有解决的问题,能量平衡法基于驻波假设,不能考虑导线的动力特性,计算误差较大,有限差分法常常假定导线微风振动稳定时的振动形态为一正弦曲线,而当存在防振锤时,导线振动曲线形态会存在明显的突变点,且以上方法均不能考虑导线几何非线性对振动过程的影响。
喻莹[13-15]等采用了有限质点法对构件进行了屈曲及倒塌分析,该方法在计算构件的动力非线性问题上有较明显的优势。本文将该方法用于输电导线微风振动响应计算中,先对能量平衡法计算微风振动响应的基本原理进行简单的陈述,再介绍有限质点法的基本计算原理,针对某些工况将两者计算的结果进行对比,以研究导线微风振动防振方案。
1 能量平衡法
能量平衡法的原理是在导线振动时,由风输入给导线系统的振动能量与导线系统内消耗的能量达到平衡,从而确定导线稳定振动的振幅。
用Pw表示单位时间内风输给导线的风能,称为风能功率;Pc表示输电线振动时消耗的功率,也就是导线的自阻尼功率;Pd表示防振装置消耗的功率。Pw、Pc和Pd均为振幅A和频率f的函数,针对某一频率f0,它们只是振幅A的函数,如图1所示,其中曲线1表示风输入功率,曲线2和曲线3分别表示不带防振锤和带防振锤时导线与防振锤消耗的功率之和,Aa和Ab表示在曲线交点a和b时对应的振幅,交点处导线-防振锤消耗的功率与风输入功率相等。本文仅考虑无防振装置的情况。

图1 能量平衡法
1.1 风能功率
研究表明,导线发生微风振动时风输给导线的能量和导线的构件参数以及风速相关。由于目前国内还没有专门的风能试验相关数据,因此还需借鉴国外的研究成果。几十年来,各国的许多学者做了大量的风洞试验和理论研究,其中国内使用较多的是Diana & Falco[16-17]关于风能输入功率的研究成果。其风能功率采用如下表达式:
(1)
式中:D为导线直径,mm;a1=0.052 6,a2=1.407 4,a3=4.032 4为常数;y0为双振幅,mm。
1.2 导线自阻尼功率
输电线的自阻尼功率是指自身在振动过程中消耗的功率,表示其振动时自身消耗或吸收振动能量的能力,也是导线消耗微风振动能量的重要因素之一,其值越大越有利于防振。
国内在导线的自阻尼测试中,多采用如下形式的表达式
(2)
式中:Pc为导线的消耗能量,mW/m;f为振动频率,Hz;K、α、β为与频率有关的试验系数。
2 有限质点法
有限质点法是基于“点值描述”和“路径单元”的基本概念,将构件离散为质点来描述其力学模式,称之为构件的点值描述,同时将质点受力后的运动在时间域上划分为许多微段,由一组离散时间点上的值来描述质点运动的轨迹,称之为途径单元。质点的运动遵循牛顿第二定律,通过虚拟的“逆向运动”求得单元纯的变形,由此求解单元内力。
2.1 点值描述
向量式力学认为构件可看成是由无数多个质点组合成的物理连续体,根据精准度要求和问题的性质,在无限多个点中选择一组有限数目的点,由这些有限个点的位置向量来描述构件的几何形状与空间位置,而这组杆件质点的总数和质点的配置方法可以任意选择。将构件ab划分为若干质点,如图2所示。

图2 构件的点值描述
质点的主要性质为:质点只承受集中力的作用;质点间是通过没有质量的单元连接的;质点的运动决定单元的节点位移;单元与单元之间相互独立,可针对各个单元分别计算其内力和变形,不需要集成整体。
2.2 途径单元描述
构件在外力作用下,质点的位置向量是时间的函数,称为途径或时间轨迹。有限质点法中质点的轨迹是用一组离散时间点上的点值来描述的。设分析的初始及终结的位置向量分别为xa和xb,时间点分别为t0和tf,将整个分析的时间过程用一组时间点t0,t1,t2,…,ta,tb,…,tf分开,并假设分析过程是一组连接的时间段,ta-tb时段表示一个途径单元,如图3所示。

图3 途径单元
假设在一个途径单元之内,内力和变形满足以下条件:以构件的初始形态作为计算其位移、变形和应力的基础构架;构件的变形很小,转动可视为中度大转动;可以忽略几何变化对构件的变形和内力计算的影响;构件的组合和约束及构件的性质不改变。
2.3 单元及单元变形描述
构件离散成质点后,质点间通过单元连接,质点间的相互内力关系通过单元的纯变形来反映。常见的连接单元有梁单元与杆单元,杆单元只可产生轴向变形,梁单元不仅能产生轴向变形,还能产生弯曲和扭转变形。
将导线离散为有限个质点,外荷载直接作用在质点上,利用式(3)所示的牛顿第二定律求解。
(3)
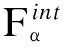
(4)
3 导线微风振动分析
本文采用有限质点法对导线进行微风振动分析,通过建立导线有限质点法的计算模型,选取合适的微风激励力和导线自阻尼力来求解导线微风振动响应。
3.1 导线微风振动计算模型
利用有限质点法对输电导线进行微风振动分析时,可先将长度为L的导线AB划分为有限个质点,再设置途径单元,其计算模型如图4所示。

图4 导线的计算模型
3.2 微风激励力
在稳定的风场中,风在刚性圆柱体背面形成的稳定漩涡脱落,在圆柱体上作用一升力Fy,且认为该升力的幅值是按正弦规律变化的,即Fysinωt。又设导线振动时垂直位移y=-A0cos(ωt-φ),其中A0为单振幅,ω为振动圆频率。在半个周期T/2内,风输入给导线功率的平均值
其中ω=2πf,在共振时cosφ=1,故有
(5)
Fy和A0均为沿输电线方向空间坐标x的函数,则
(6)
将Diana & Falco风能输入功率表达式(1)代入式(6)中,得:
(7)
3.3 导线自阻尼力
与常见的粘滞阻尼系统不同,导线的阻尼机理十分复杂,常将其等效为经典粘滞阻尼。国内导线的自阻尼功率
(8)
又由构件动力学的知识可知,含有粘滞阻尼的单自由度体系在简谐荷载作用下阻尼力在一个周期内消耗的能量

式中:fd为导线阻尼力;c为导线的阻尼系数。
令单自由度体系在一个周期消耗的能量与长度为Δl导线的自阻尼消耗能量相同,即
(10)
可解得
(11)
在有限质点法中,常通过施加虚拟的阻尼力来考虑构件的阻力作用,虚拟阻尼力
(12)
于是有ξ=c/m。
综合以上分析,利用有限质点法计算输电导线微风振动响应的计算流程如图5所示。
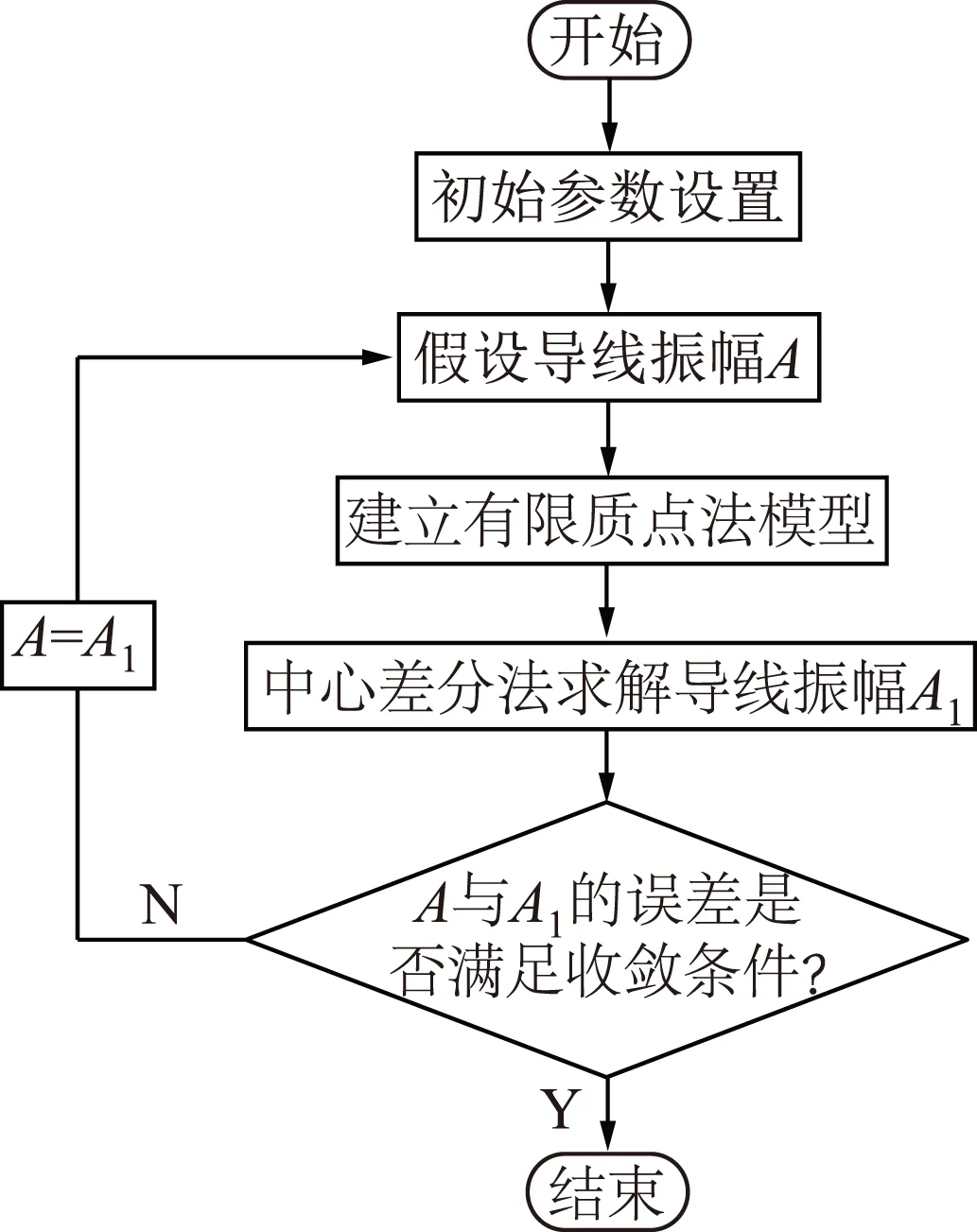
图5 微风振动响应计算流程
4 算例分析
为了验证以上有限质点法求解的正确性,本节利用程序分别计算以下几个算例,并与能量平衡法的结果对比。
4.1 算例1:导线受分布正弦激励振动
以LGJ-500/450型号导线为例,其主要物理参数见表1。

表1 导线特性参数
导线两端受水平张力作用,档距L=300 m,在竖直方向上作用正弦均布荷载qsin(ωt),其中正弦均布力的幅值为100/L(N/m),激励频率f=1 Hz,设导线单位长度阻尼系数c=0.1 Ns/m2。采用有限质点法计算导线在上述正弦均布荷载作用下的振动响应,其中跨中质点的位移与速度时程图如图6、7所示。

图6 导线跨中点位移时程图
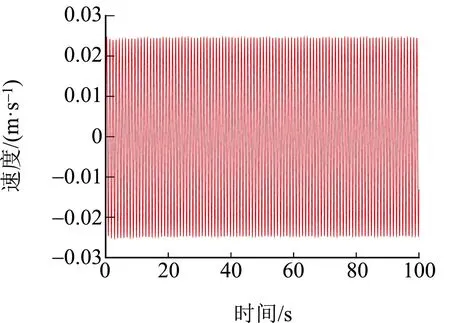
图7 导线跨中点速度时程图
由导线跨中点振动的位移和速度时程曲线可知,在施加均布正弦荷载25 s后导线振动达到稳定,稳定时的双振幅为8.3 mm左右, ANSYS计算得到的稳定双振幅8.9 mm,图8所示。
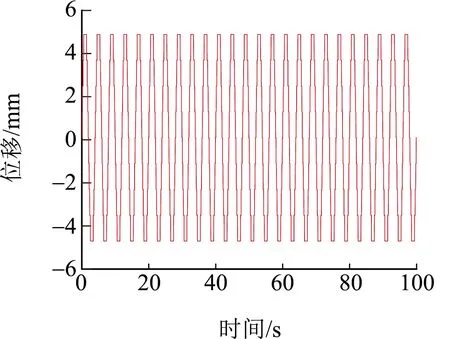
图8 ANSYS计算导线跨中点速度时程图
通过对比,表明有限质点法计算具有较高的精确性,质点稳定后的速度和位移均随时间呈正弦规律振动,且振动频率与荷载激励频率保持一致。
4.2 算例2:导线微风振动响应
为验证有限质点法在导线微风振动响应计算方面的精确性,取档距L=300 m,运行张力为拉断力的18%的导线为例,计算工况见表2。
表2 导线微风振动分析工况

工况编号风速/(m·s-1)频率f/Hz121622.520332443.528543264.536
利用有限质点法,采用MATLAB编程,分别对表2中的6种工况进行微风振动响应计算分析,取导线1 m为一个单元,初步估算得风激励的周期为0.005 s左右,取h=0.000 1 s为一个计算时间步长,绘出风速为2 m/s、3 m/s、4 m/s时导线微风振动的位移时程曲线,由于导线的初速度为零,在风荷载作用下,导线会经历一段不稳定的振动过渡期,最终在阻尼的作用下达到稳定,图9给出了风速为2 m/s时导线微风振动整个时间历程的位移时程曲线,风速为3 m/s、4 m/s时仅给出了导线微风振动接近稳定至稳定振动的位移时程曲线,分别如图10、11所示。
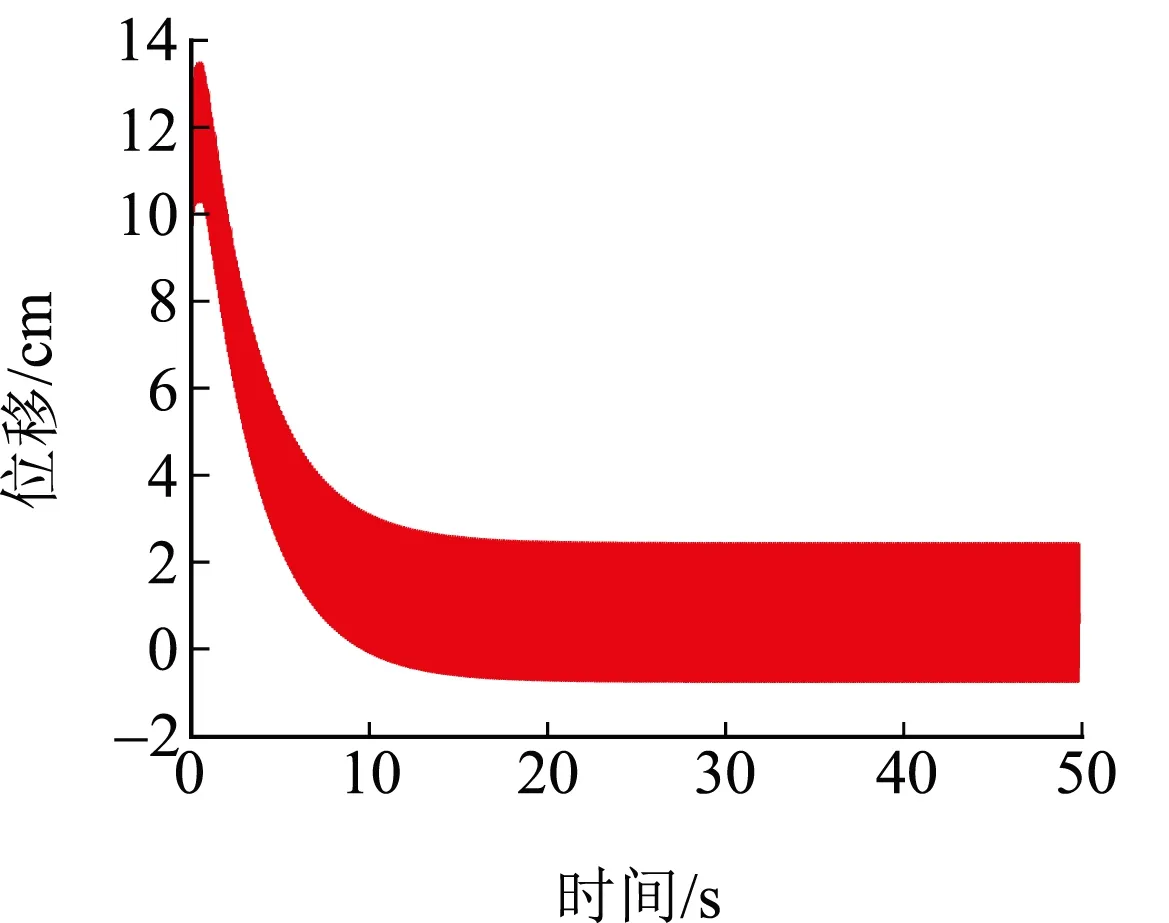
图9 风速为2 m/s时微风振动

图10 风速为3 m/s时微风振动
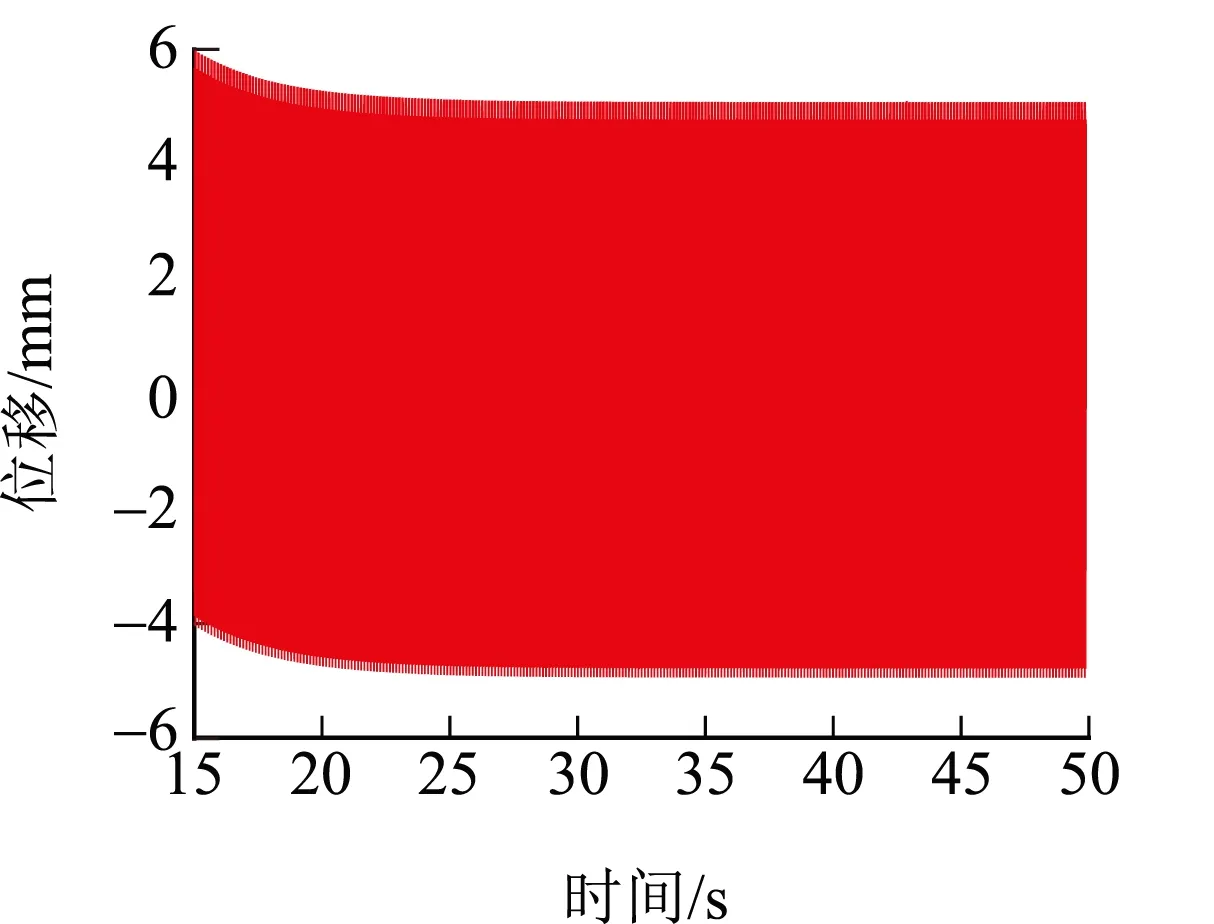
图11 风速为4 m/s时微风振动
表3给出了不同风速下有限质点法和能量平衡法计算得到的导线微风振动位移响应。
表3 导线微风振动响应计算结果

编号风速/(m·s-1)振动响应/mm有限质点法能量平衡法12.00.01720.019322.50.01330.015133.00.01060.012043.50.00810.009554.00.00520.006864.50.00280.0020
由表3可以看出两种方法得到的结果比较接近,证明了有限质点法在导线微风振动响应计算上的正确性,同时由于有限质点法在计算分析时无需形成复杂的非线性刚度矩阵,也不需要进行反复迭代求解,因此其计算速度较有限单元法要快很多。
5 结论
a) 通过将有限质点法运用到导线微风振动计算分析中,考虑了导线的质量及几何非线性,并将计算得到的结果与能量平衡法进行对比,表明有限质点法在导线微风振动计算上的正确性。
b) 与有限单元法相比,利用有限质点法进行导线微风振动计算分析时,既不用形成复杂的非线性单元刚度矩阵,也无需进行反复迭代求解,计算速度较快。
c) 将有限质点法引入到导线微风振动响应计算分析中,为研究输电导线微风振动防振方案打下了基础。
[1] 邵天晓. 架空送电线路的电线力学计算[M]. 北京:中国电力出版社, 2003.
[2] 郑玉琪. 架空输电线微风振动[M]. 北京:水利水电出版社, 1987.
[3] 谢强,张勇,李杰. 华东电网500 kV任上5237线飚风致倒塔事故调查分析[J]. 电网技术,2006,30(10):59-63.
XIE Qiang, ZHANG Yong, LI Jie. Inverstigation on Tower Collapses of 500 kV Renshang 5237 Transmission Lines Caused by Downburst[J]. Power System Technology, 2006, 30(10): 59-63.
[4] 王松平,陈笃. 均匀和风作用下输电线振动分析[J]. 武汉汽车工业大学学报,1997,19(3):70-74.
WANG Songping, CHEN Du. Analysis of Transmission Lines Vibration Under Well-distributed Breeze Loads[J]. Journal of Wuhan Automotive Polytechnic University, 1997, 19(3): 70-74.
[5] 梁政平,王乘,孔德怡,等. 特高压架空输电线微风振动影响因素分析[J]. 水电能源科学,2008,26(3):185-204.
LIANG Zhengping,WANG Cheng,KONG Deyi,et al. Analysis of Aeolian Vibration Influence Factors on UHV Transmission Conductor[J]. Water Resources and Power,2008,26(3):185-204.
[6] 李庆峰,魏杰,殷禹,等. 复合绝缘子耐张串微风振动疲劳特性研究[J]. 电网技术,2012,36(12):269-275.
LI Qingfeng,WEI Jie,YIN Yu,et al. Research on Aeolian Vibration Caused Fatigue Properties of Strain Composite Insulator String[J]. Power System Technology,2012,36(12):269-275.
[7] 吴海洋,包永忠,杨艺. 输电线路钢管塔构件微风振动分析[J]. 电力建设,2009,30(9):42-45.
WU Haiyang,BAO Yongzhong,YANG Yi. Analysis of Aeolian Vibration of Transmission Tower Steel Tube Member[J]. Electric Power Construction,2009,30(9):42-45.
[8] 侯景鹏,吴兴宏,孙自堂. 防振锤-输电线体系微风振动的研究与进展[J]. 合肥工业大学学报(自然科学版),2011,34(5):743-747.
HOU Jingpeng,WU Xinghong,SUN Zitang. Advances in the research on wind oscillation of vibration damper-transmission system[J]. Journal of Hefei University of Technology(Natural Science),2011,34(5):743-747.
[9] 孔德怡. 基于动力学方法的特高压输电线微风振动研究[D]. 武汉:华中科技大学,2009.
[10] VECCHIARELLI J,CURRIE I G,HAVARD D G. Computational Analysis of Aeolian Conductor Vibration with a Stockbridge-type Damper[J]. Journal of Fluids and Structure, 2000(14) :489-509.
[11] 李黎,叶志雄,孔德怡,等. 输电线微风振动分析方法能量平衡法的改进研究[J]. 工程力学,2009,26(S):176-180. LI Li,YE Zhixiong,KONG Deyi,et al. Improvement of Energy Balance Method and Analysis of Aeolian Vibration on UHV Transmission Lines[J]. Engineering Mechanics, 2009, 26(S): 176-180.
[12] 孔德怡,李黎,龙晓鸿,等. 特高压架空输电线微风振动有限元分析[J]. 振动与冲击, 2007,26(8):64-68.
KONG Deyi,LI Li,LONG Xiaohong,et al. Analysis of Aeolian Vibration of UHV Transmission Conductor by Finite Element Method[J]. Engineering Mechanics, 2007, 26(8): 64-68.
[13] 喻莹,许贤,罗尧治. 基于有限质点法的结构动力非线性行为分析[J]. 工程力学,2012,29(6):63-69.
YU Ying, XU Xian, LUO Yaozhi. Dynamic Nonlinear Analysis of Structures Based on the Finite Particle Method[J]. Engineering Mechanics,2012,29(6): 63-69.
[14] 喻莹,罗尧治. 基于有限质点法的结构倒塌破坏研究I:基本方法[J]. 建筑结构学报, 2011,32(11): 17-26.
YU Ying, LUO Yaozhi. Structural Collapse Analysis Based on Finite Particle Method I:Basic Approach[J]. Journal of Building Structures, 2011, 32(11): 17-26.
[15] 喻莹,罗尧治. 基于有限质点法的结构屈曲行为分析[J]. 工程力学,2009,26(10):23-29.
YU Ying, LUO Yaozhi. Buckling Analysis of Structures by the Finite Particle Method[J]. Engineering Mechanics,2009,26(10): 23-29.
[16] DIANA G,CIGADA A,BELLOLI M. Stockbridge-type Damper Effectiveness Evaluation: Part I- Comparison Between Tests on Span and on the Shaker[J]. IEEE Transactions on Power Delivery, 2003, 18(4): 1462-1469.
[17] DIANA G,MANENTI A,PIROTTA C. Stockbridge-type Damper Effectiveness Evaluation: Part II- the Influence of the Impedance Matrix Terms on the Energy Dissipated[J]. IEEE Transactions on Power Delivery,2003,18(4):1470-1477.
(编辑 王朋)
Aeolian Vibration of Power Transmission Conductors Based on Finite Particle Method
XIE Wenping1, XU Ningbo2, LUO Xiaoyu1, LI Li2
(1.Electric Power Research Institute of Guangdong Power Grid Co., Ltd., Guangzhou, Guangdong 510080, China; 2. School of Civil Engineering & Mechanics, Huazhong University of Science & Technology, Wuhan, Hubei 430074, China)
In allusion to the problem of increasingly damage to lines by aeolian vibration of ultrahigh voltage transmission conductors, this paper uses finite particle (FPM) to study aeolian vibration. Point value description is used to disperse structures into particles and particles are linked by elements. Movement of particles should follow Newton’s second law and the central differential method is used for solving movement of particles so as to tracking action of structures. Calculation discovers FPM considers influence of qualities of power transmission lines and geometric nonlinear, which can make calculation results more authentic. Finally, FPM is used to calculate response of aeolian vibration of conductors under different wind excitation conditions and the result is basically identical to that of energy balance method (EBM), which proves validity of FPM.
aeolian vibration; energy balance method (EBM); finite particle method (FPM); vector mechanics of structure
2016-07-05
2016-08-30
中国南方电网有限责任公司科技项目(GDKJ00000014)
10.3969/j.issn.1007-290X.2016.10.022
TU393
A
1007-290X(2016)10-0127-06
谢文平(1986),男,江西抚州人。工程师,工学硕士,主要从事结构抗风研究。
徐宁波(1991),男,湖北荆州人。在读硕士研究生,主要从事结构减振研究。
罗啸宇(1988),男,湖北黄冈人。工程师,工学博士,主要从事结构抗风研究。
