一种基于时变概率权的短期风功率组合预测模型
2016-11-23杨苹叶超
杨苹,叶超
(1. 华南理工大学 电力学院,广东 广州 510640;2. 广东省绿色能源技术重点实验室,广东 广州 511458; 3. 风电控制与并网技术国家地方联合工程实验室,广东 广州 511458)
一种基于时变概率权的短期风功率组合预测模型
杨苹1,2,3,叶超1,2
(1. 华南理工大学 电力学院,广东 广州 510640;2. 广东省绿色能源技术重点实验室,广东 广州 511458; 3. 风电控制与并网技术国家地方联合工程实验室,广东 广州 511458)
高精度的短期风功率预测有利于实现接入大量风机的电力系统优化调度。针对自回归滑动平均(auto-regressive and moving average,ARMA)、反向传播(back propagation,BP)神经网络、最小二乘支持向量机(least squares support vector machine,LS-SVM)等单一模型预测不稳定的问题,以及协方差、概率权组合模型权重固定的不足,结合风功率的日变化特性,提出一种基于时变概率权的组合预测模型。实际算例表明:组合模型能有效提高风功率预测的精度,而时变概率权组合模型能够动态调整各单一模型的权重,进一步提高预测精度。
短期风功率预测;单一模型;组合模型;时变概率权
2014年全球风电新增装机容量51 477 MW,年增长率高达44%[1]。风力发电带来了巨大的经济效益,但由于其输出的波动性,风电并网会对电网造成冲击[2-4]。为了更好地实现电力系统的优化调度,提高风能利用率,研究精度更高的风功率预测模型具有十分重要的现实意义。
根据所采用数学模型的不同,风功率预测模型可分为持续预测模型、物理模型和统计模型[5-6]。持续预测法把最近一点的实测值作为下一时刻的预测值,并认为风速预测值等于最近几个风速值的滑动平均值[7]。物理模型通常结合数值天气预报(numeral weather prediction,NWP)进行预测,其最大的优势在于不需要大量的风电场历史出力数据,因此特别适合新建风电场的功率预测[8]。统计模型则根据风电场历史出力数据分析天气状况与风电功率的关系,然后利用实测的NWP数据对风电场输出功率进行预测,常用的预测方法有人工神经网络方法、蚁群优化和支持向量机等[9-10]。文献[8]提出基于NWP的物理预测模型,但其未考虑风电场的尾流效应,预测误差仍较大。文献[9]建立了基于人工神经网络的风电功率预测模型,但其采用的梯度下降法寻优易陷入到局部最优解。
物理模型和统计模型有着各自的优缺点,若采用组合模型,将二者的优点结合起来,可大大提高风功率预测的准确度[11-12]。考虑到实际风功率分布大多为非正态分布,本文采用概率权确定各子模型的权重,并针对其权重固定的不足,提出一种基于时变概率权的组合预测模型。实际算例计算结果表明:组合模型的整体预测精度高于单一模型,协方差、概率权组合模型均可较好地预测风功率变化趋势,而本文提出的时变概率权组合模型可在风速改变时通过调整各单一模型的权重,进一步地提高预测精度。
1 单一预测模型
1.1 自回归滑动平均预测模型
建立自回归滑动平均(auto-regressive and moving average,ARMA)模型时,需要首先对原始数据序列平稳化处理,将非平稳的数据序列转换为平均值为0的平稳数据序列。
对于长度为N的风速序列{xt},其平均值[7]
(1)
对序列{xt}作平稳化处理,可得新的序列{yt}:
(2)
根据{yt}可建立ARMA模型(p,q):
(3)
式中:φi为自回归参数;at为服从正态分布的白噪声序列;θj为滑动平均参数。
利用AIC(Akaike Information Criterion)准则确定ARMA模型的p、q值,利用最小二乘法估计模型参数φi、θj。
图1为根据某风电场实际的风速-功率点,利用比恩法拟合得到的风电场风速-功率曲线,风电场输出功率
(4)
式中v为当前时刻的风速。

图1 拟合风电场风速-功率曲线
根据ARMA模型预测得到的风速值,将其带入式(4),即可得到当前时刻的预测风功率值。
1.2 反向传播神经网络模型
反向传播(back propagation,BP)神经网络能够以任意精度逼近任何非线性映射,可以学习未知信息,并具备一定的容错性,因此构造出来的系统具有较好的鲁棒性,特别适合处理复杂的问题。图2为BP神经网络的基本结构。

图2 BP神经网络基本结构
BP神经网络采用梯度下降法寻找最优解,但往往会陷入到局部最小值中。为了能够实现全局寻优,可采用遗传算法对BP神经网络的初值进行优化[13]。遗传算法主要包括以下步骤:
a)初始种群。个体为可能解,包括神经网络的权值和阈值,利用实数对个体进行编码,确定输入层、隐含层、输出层的权值和阈值。
b)适应度函数。利用BP神经网络对原始数据进行训练可得到预测输出,预测输出与实际输出差异越小,个体适应度越高。个体适应度
(5)
式中:m为BP输出层节点数;Yj、Oj为第j个节点的实际输出和预测输出。
c)选择、交叉、变异。选择可以保留适应度高的个体,以提高预测结果的准确性;交叉操作可将个体重组,以得到新的个体;变异操作常对个体的某一位进行变异,以增加个体的多样性。
1.3 最小二乘支持向量机模型
最小二乘支持向量机(least squares support vector machine,LS-SVM)具有较强的泛化能力,遵守风险最小化的原则,对于非线性问题,首先将其转化为高维度空间的线性化问题,用核函数替代高维度空间的内积运算,有效地解决了维数灾难和局部极值的问题,并且计算速度比一般的SVM更高[14]。
假设存在样本集合z={(x1,y1),…,(xt,yt)},根据风险最小化原理,样本z的最小二乘向量机问题可转化为约束最优化问题:
(6)
(7)
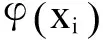
式(6)可用拉格朗日法求解:

式中:L为目标函数;αi为回归系数。
求解式(8)的偏导数,可将其转化为对如下方程组的求解:


(10)
2 基于概率权确定模型权重方法
单一预测模型容易实现,同时也容易出现预测结果不稳定的问题。组合模型通过加权将单一模型结合起来,减少了单一模型的偶然误差,从而提高预测精度,为此提出了一种基于概率权确定模型权重的方法。
2.1 概率权原理
目前,求解组合模型中单一模型权重的方法多假设风功率呈正态分布或近似正态分布。但实际风功率的分布具有不规则性,难以满足此要求。为此,采用概率权的方法确定各子模型的权重。

(11)
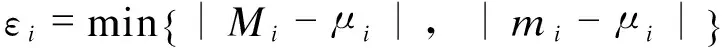

2.2 概率权确定各子模型权重
假设有n个风功率预测单一模型,t时刻模型l的预测风功率值为xlt,则利用概率权确定各子模型权重的步骤如下:

(12)
b)确定预测时段内风功率值xlt的上限Ml和下限ml,ml=min{xlt},Ml=max{xlt}。
c)利用切比雪夫不等式确定pl=P{ml≤Xl≤Ml}的最小值plmin。
d)求取各单一模型的权重
(13)
e)样本点数S值优化。设xlj为j时刻子模型l的风功率预测值,sj为j时刻的风功率真实值,以各个子模型的预测方差最小为目标函数,即:
(14)
当u取最小值时,此时的S即为最优选用的样本个数。
f)根据步骤e)中求取的最优S值,将其代入步骤a)—d),即可得到各个子模型的权重。
3 基于时变概率权的子模型权重优化
利用概率权确定各子模型的权重方法需要利用历史风功率数据分析计算,随着预测时间的推移,使用固定的子模型权重难以有效地反映风电场的状态变化特性。为了进一步提高预测模型的精度,本文提出一种基于时变概率权确定子模型权重的方法,其实现步骤如下:
a)动态更新存储的历史风功率数据,历史风功率数据的最大存储量为96×3,每隔1 h更新一次,每次更新1×4个数据;
b)利用2.2节中的方法求取各子模型的权重;
c)每隔1 h,根据新的历史风功率数据样本重新计算各单一模型的权重。
基于时变概率权确定子模型权重方法的流程如图3所示。

图3 基于时变概率权确定子模型权重方法的流程
4 实例分析
以我国某地含24台双馈异步风力发电机(额定有功功率1.5 MW)的风电场为例,预测未来24 h的风功率值,每隔15 min预测一次,共计96个点。利用相对偏差(relative deviation,RD,其值记为dr)和归一化均方根误差(mean absolute percent error,MAPE,其值记为EMAP)评估各模型的预测误差。
(15)
(16)
式中:pai为风电场实际功率;ppi为模型预测功率;pN为风电场额定功率;M为预测点数,取96。
4.1 单一预测模型
单一预测模型包括ARMA、BP和LS-SVM模型3种。图4为3种单一预测模型的风功率预测值,图5为3种单一预测模型预测值的相对偏差。

图4 单一预测模型的预测结果
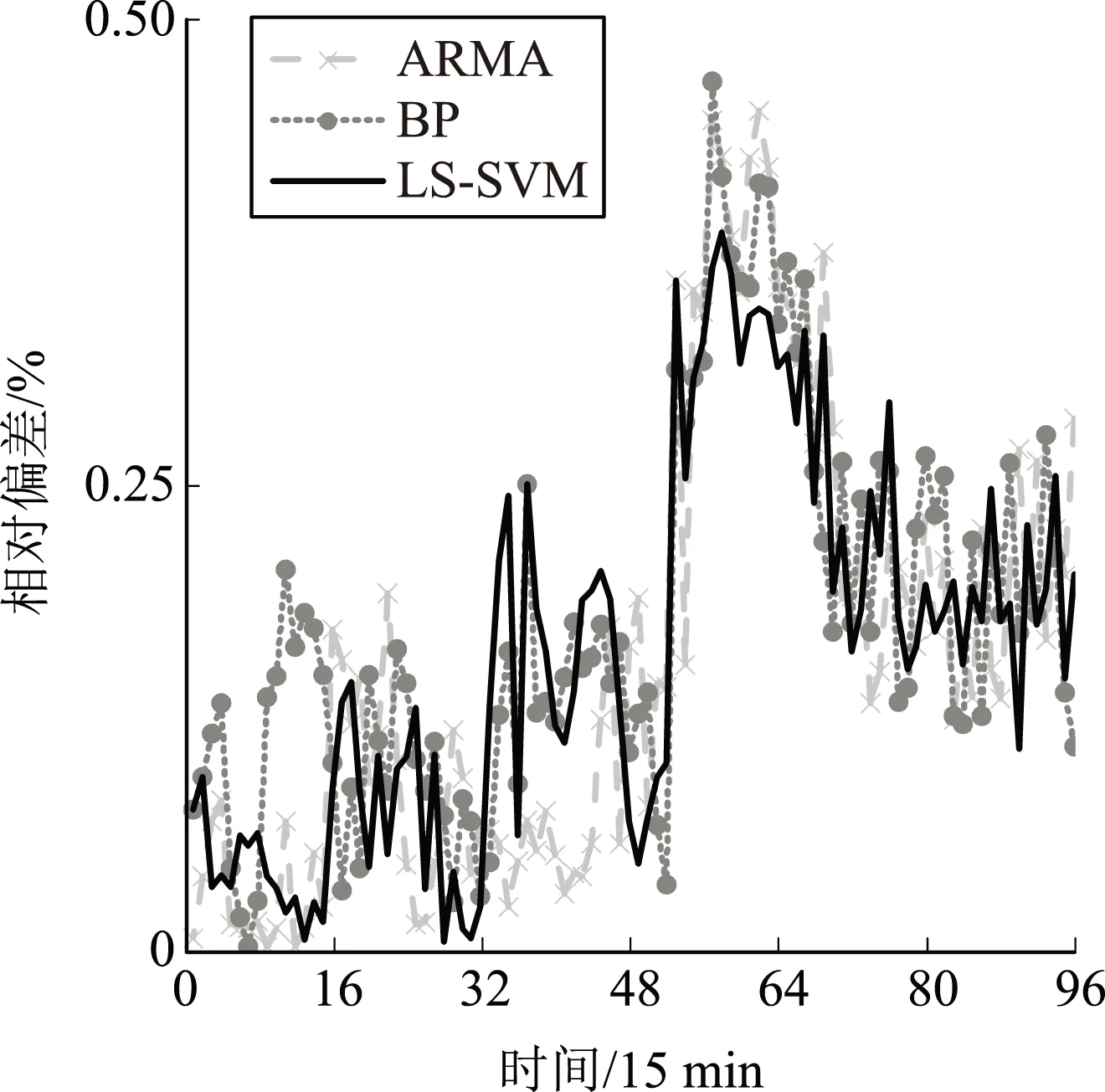
图5 单一预测模型预测值与实际值的相对偏差
从图4和图5可以看出,风电场风速波动较小时,单一预测模型可较好地预测风电场的输出功率;风速阶跃时,预测误差较大,利用式(16)计算得到各模型的MAPE见表1。
表1 单一预测模型的预测误差

模型EMAP/%ARMA18.2BP16.6LS-SVM17.1
可见,单一预测模型只能在某一时间段内保持较高的预测精度,整体预测误差仍较大,因此有必要对其进行改进。
4.2 组合预测模型
考虑到组合模型可减少单一预测模型带来的偶然误差,本文分别建立了协方差、概率权、时变概率权3种组合模型并进行风功率的预测。图6为3种组合模型的风功率预测结果,图7为组合模型的相对偏差。

图6 组合预测模型的预测结果

图7 组合预测模型预测值与实际值的相对偏差
根据式(16)计算得到的3种组合模型的MAPE见表2。
表2 组合预测模型的预测误差
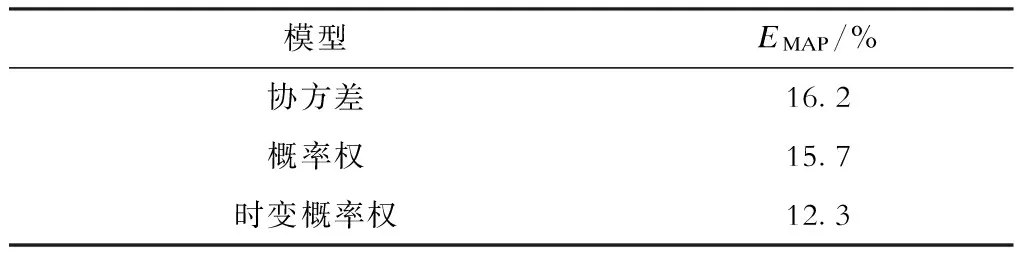
模型EMAP/%协方差16.2概率权15.7时变概率权12.3
对比图4和图6可知,组合预测模型减少了单一预测模型的偶然误差,因而整体预测精度更高,能更好地反映风功率的变化趋势。
相比协方差组合预测模型,本文提出的改进概率权模型不需要历史样本风功率数据严格满足正态分布,可避免因样本数据不规范对子模型权重计算的影响,适用性更强。此外,本文提出的预测模型可在风速阶跃初期,通过动态更新历史存储数据,及时调整各子模型的权重系数,因此预测精度最高。
5 结论
基于对已有单一预测模型及协方差、概率权组合预测模型不足的分析,提出了基于一种时变概率权的短期风功率组合预测模型。通过实例分析得到以下结论:
a)单一预测模型可以预测风功率的变化趋势,但其整体的预测误差较大;
b)组合预测模型能够减少单一预测模型带来的偶然误差,提高了整体的预测精度;
c)时变概率权组合预测模型可在风速大扰动时动态调整各单一子模型的权重,因而预测精度最高。
[1] 全球风能理事会(GWEC). 2014年全球风电装机容量统计[J]. 风能,2015(2):50-53.
Global Wind Energy Council(GWEC). 2014 Global Wind Power Installed Capacity Statistics [J]. Wind Energy,2015 (2):50-53.
[2] 迟永宁,刘燕华,王伟胜,等. 风电接入对电力系统的影响[J]. 电网技术,2007,31(3):77-81.
CHI Yongning,LIU Yanhua,WANG Weisheng,et al. Study on Impact of Wind Power Integration on Power System[J]. Power System Technology,2007,31(3):77-81.
[3] 汤蕾,沈沉,张雪敏. 大规模风电集中接入对电力系统暂态功角稳定性的影响(二):影响因素分析[J]. 中国电机工程学报,2015,35(16):4043-4051.
TANG Lei,SHEN Chen,ZHANG Xuemin. Impact of Large-scale Wind Power Centralized Integration on Transient Angle Stability of Power Systems-Part II:Factors Affecting Transient Angle Stability[J]. Proceedings of the CSEE,2015,35(16):4043-4051.
[4] CHOMPOO-INWAI C,LEE W,FUANGFOO P,et al. System Impact Study for the Interconnection of Wind Generation and Utility System[J]. IEEE Transactions on Industry Applications,2005,41(1):163-168.
[5] 薛禹胜,郁琛,赵俊华,等. 关于短期及超短期风电功率预测的评述[J]. 电力系统自动化,2015(6):141-151.
XUE Yusheng,YU Chen,ZHAO Junhua,et al. A Review on Short-term and Ultra-short-term Wind Power Prediction[J]. Automation of Electric Power Systems,2015(6):141-151.
[6] 谷兴凯,范高锋,王晓蓉,等. 风电功率预测技术综述[J]. 电网技术,2007(S2):335-338.
GU Xingkai,FAN Gaofeng,WANG Xiaorong,et al. Summarization of Wind Power Prediction Technology[J]. Power System Technology,2007(S2):335-338.
[7] WANG C,YAN W. Short-term Wind Speed Prediction of Wind Farms Based on Improved Particle Swarm Optimization Algorithm and Neural Network[C]// 2010 International Conference on Mechanic Automation and Control Engineering(MACE). Wuhan:IEEE,2010.
[8] 王丽婕,冬雷,高爽. 基于多位置NWP与主成分分析的风电功率短期预测[J]. 电工技术学报,2015,30(5):79-84.
WANG Lijie,DONG Lei,GAO Shuang. Wind Power Short-term Prediction Based on Principal Component Analysis of NWP of Multiple Locations[J]. Transactions of China Electrotechnical Society,2015,30(5):79-84.
[9] BARBOUNIS T G,THEOCHARIS J B. Locally Recurrent Neural Networks for Wind Speed Prediction Using Spatial Correlation[J]. Information Sciences,2007,177(24):5775-5797.
[10] SHI J,YANG Y,WANG P,et al. Genetic Algorithm-piecewise Support Vector Machine Model for Short Term Wind Power Prediction[C]//2010 8th World Congress on Intelligent Control and Automation(WCICA).Jinan:IEEE,2010.
[11] 叶林,刘鹏. 基于经验模态分解和支持向量机的短期风电功率组合预测模型[J]. 中国电机工程学报,2011,31(31):102-108.
YE Lin,LIU Peng. Combined Model Based on EMD-SVM for Short-term Wind Power Prediction[J]. Proceedings of the CSEE,2011,31(31):102-108.
[12] 张学清,梁军,张熙,等. 基于样本熵和极端学习机的超短期风电功率组合预测模型[J]. 中国电机工程学报,2013,33(25):33-40.
ZHANG Xueqing,LIANG Jun,ZHANG Xi,et al. Combined Model for Ultra Short-term Wind Power Prediction Based on Sample Entropy and Extreme Learning Machine [J]. Proceedings of the CSEE,2013,33(25):33-40.
[13] 史洁. 风电场功率超短期预测算法优化研究[D]. 保定:华北电力大学,2012.
[14] 刘纯,范高锋,王伟胜,等. 风电场输出功率的组合预测模型[J]. 电网技术,2009(13):74-79.
LIU Chun,FAN Gaofeng,WANG Weisheng,et al. A Combination Forecasting Model for Wind Farm Output Power[J]. Power System Technology,2009(13):74-79.
(编辑 彭艳)
A Combination Forecasting Model for Short-term Wind Power Combination Based on Time Varying Probability Weight
YANG Ping1,2,3, YE Chao1,2
(1.School of Electric Power, South China University of Technology, Guangzhou, Guangdong 510640, China; 2. Guangdong Key Laboratory of Clean Energy Technology, Guangzhou, Guangdong 511458, China; 3. National-local Joint Engineering Laboratory for Wind Power Control and Integration Technology, Guangzhou, Guangdong 511458, China)
High-precision short-term wind power forecasting is useful to realize optimizing dispatching of the power system with a large number of wind turbines. In allusion to the problem of unstable forecasting of some single models such as auto-regressive and moving average (ARMA), back propagation (BP) neutral network, least squares support vector machine (LS-SVM) and so on, as well as shortages of fixed weight of covariance and the probability weight combined model, this paper presents a kind of combined forecasting model based on time varying probability by combining with daily variation characteristic of wind power. Practical examples indicate that the combined model can effectively improve precision of forecasting while the time varying probability weight combined model can dynamically adjust weight of each single model and further improve forecasting precision.
short-term wind power forecasting; single model; combined model; time varying probability weight
2016-07-11
国家科技支撑计划项目(2015BAA06B02);广东省科技计划项目(2012B040303005);南沙区科技计划项目资助(2013P005)
10.3969/j.issn.1007-290X.2016.10.001
TM73
A
1007-290X(2016)10-0001-06
杨苹(1967),女,广西钦州人。教授,博士生导师,工学博士,研究方向为可再生能源的优化运行控制与并网技术、智能微电网关键技术。
叶超(1991),男,河南南阳人。在读硕士研究生,研究方向为新能源发电并网控制、智能微电网关键技术。
