3种主动控制算法的结构振动控制效果研究

樊文华，邹万杰

（广西科技大学土木建筑工程学院，广西柳州545006）

3种主动控制算法的结构振动控制效果研究

樊文华，邹万杰*

（广西科技大学土木建筑工程学院，广西柳州545006）

针对不同类型的结构，由Matlab中的相关函数命令求出相应的控制力状态反馈增益矩阵，继而得出结构振动的位移、加速度和控制力，比较分析了3种主动控制算法的控制效果，并给出了基于Matlab的三层框架结构的算例.分析结果表明：主动控制能够有效地减小结构的地震响应，特别是当结构刚度较大时，3种主动控制算法控制效果均较理想；而当结构刚度较小时，各种控制算法的控制效果差异较大，LQR控制算法和模态控制算法的控制效果较好，而极点配置控制算法控制效果较差，甚至可能放大地震响应，需要优化极点配置得到适宜的状态反馈增益矩阵以改善结构加速度响应的控制效果.

主动控制算法；结构刚度；控制效果；Matlab

0　引言

结构振动控制是振动工程领域重要的研究方向，根据控制原理不同，可分为主动振动控制、半主动振动控制和被动振动控制［1-5］.主动控制能够根据传感元件检测到被控对象的振动信息，采用主动控制算法，通过作动器对被控对象施加控制力，从而减小或抑制被控对象的振动反应［1-2］.目前，主动控制相关技术方法已在航空航天领域、土木工程领域、交通运输领域及机械工程领域的应用中初具规模［6］.与被动振动控制方法相比，主动控制方法具有更好的适应性［7-9］.目前，结构主动控制算法主要有：LQR控制算法、模态控制算法、极点配置控制算法、自适应控制算法、鲁棒控制算法和智能控制算法等.LQR控制算法通过设定控制参数获得一定的控制效果；模态控制算法利用模态坐标变化，将系统的运动方程完全解耦，将整个结构受控系统振动转化为对各阶模态控制，大大降低控制复杂度［10］；极点配置控制算法使系统的闭环极点配置到期望位置上［11-12］；自适应控制算法所采用的控制策略大致有自适应前馈控制、自校正控制和模型参考自适应控制3大类；鲁棒控制算法是选择线性反馈律使得闭环系统的稳定性或性能对于扰动具有一定的抵抗能力；模糊控制作为智能控制的一个重要分支，为解决不易或无法建模的复杂系统控制问题提供了有力手段.文中采用3种工程中最常采用的主动控制算法对不同刚度的结构振动控制效果进行了比较分析，并得出相应的结论.

1　结构振动控制系统模型

已知结构质量矩阵M、刚度矩阵K和阻尼矩阵C，其中，结构阻尼矩阵可按Rayleigh阻尼由前两阶振型阻尼比确定，即C=αM+βK.为元素均为1的列向量.采用结构层相对地面位移坐标空间建立结构运动方程，即：

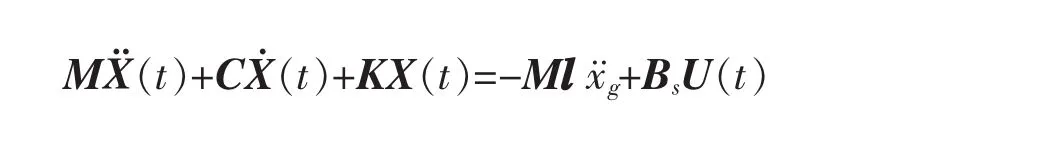
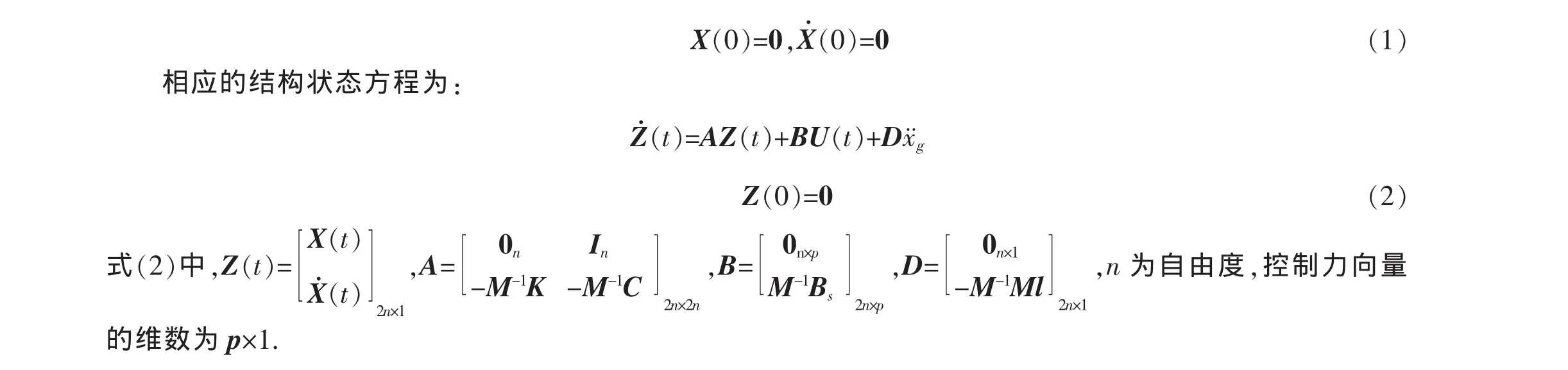
2　LQR控制算法

在采用LQR控制算法时，权矩阵Q和R是2个重要的参数，但根据现有研究成果，只能依据工程经验先确定Q和R，使其达到一定的控制效果.

设Q和R分别为：

式（3）中，α和β是待定系数.

由Matlab函数lqr可得连续状态方程的控制力反馈增益矩阵，即：

则最优控制力：

将式（4）求解得到的状态反馈增益矩阵G代入式（2），得受控结构状态方程：

由Matlab函数lsim可得结构控制系统状态反应：

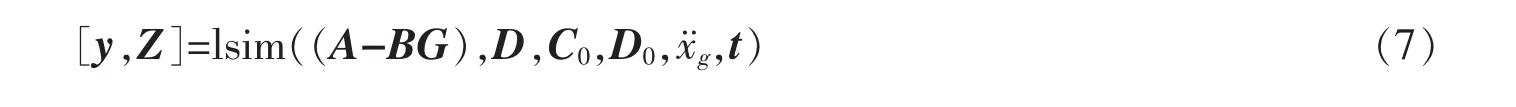
式（7）中，C0为单位矩阵，D0为零矩阵，t为地震作用时间向量，y是输出向量，它与状态向量Z相同.

3　模态控制算法

设结构反应

由于广义质量矩阵、刚度矩阵和阻尼矩阵均是对角矩阵，所以，式（9）可表示成n个独立的运动方程，再将其表示为下述独立的状态方程：

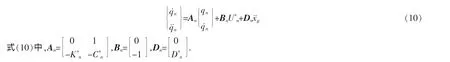
针对每一个模态坐标方程，权矩阵

由Matlab函数lqr得到每一独立广义模态坐标的反馈增益矩阵：

将其组合形成广义模态坐标状态向量反馈增益矩阵Gc=［Gc1Gc2］.则控制力表达式：

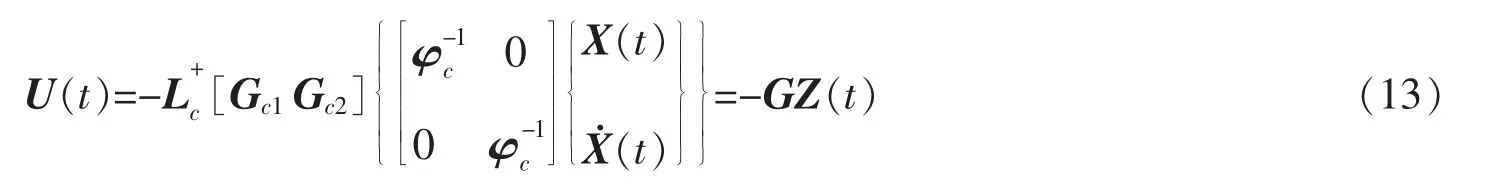
结构控制系统反应仍利用式（7）计算.

4　极点配置控制算法

由Matlab函数eig可得到结构系统矩阵A的特征值向量，即：

期望极点可以根据减振要求的阻尼比确定.

假设G的选择使下式成立：

式（16），式（17）中，Φj（λi）是Φ（λi）的第j列，ej是单位矩阵Ip的第j列，当（λiIn-A）-1存在时，rank［（λiIn-A）-1］=p.

如果λi（i=1，2，…，n）是不同的特征值，则状态反馈增益矩阵可表示为：

式（18）中，Γ=［Φj1（λ1）Φj2（λ2）…Φjn（λn）］∈Rn×n，e=［ej1ej2…ej3］∈Rp×n.

将式（18）得出的状态反馈增益矩阵G代入式（2），由Matlab函数eig得到闭环控制系统的极点为

与设定的极点相同.

结构控制系统反应仍利用式（7）计算.

5　算例

某3层框架结构，设结构层质量为mi=4×105kg，i=1，2，3［5］，假定结构前二阶振型阻尼比ζ1=ζ2=0.05.结构的激励为EI Centro（NS，1940）地震波，地震输入峰值为200 gal.为比较各种不同控制算法在不同类型结构（刚性和柔性结构）中的控制效果，结构的层间抗侧刚度ki分别取不同的值，采用上述3种主动控制算法计算结构控制系统反应及控制力.为衡量结构各种控制算法的减震效率，定义别为无控及施加控制力时的地震反应，δi为第i层减震效率，δi越大，减震效率越高.

对于普通结构，可取ki=p×107N／m，p=2，…，10［5］.结构振动响应见图1～图2（只给出结构抗侧刚度ki=7×107N／m时，第3层的位移、加速度，其他层类似），减震效率见图3～图4.

通过计算分析，从图1～图2中看出，无控时结构的第3层位移和加速度比用3种主动控制算法控制时的第3层位移和加速度都要大（其他层类似）.从图3～图4中可看出，主动控制能够显著地减小结构的地震响应.

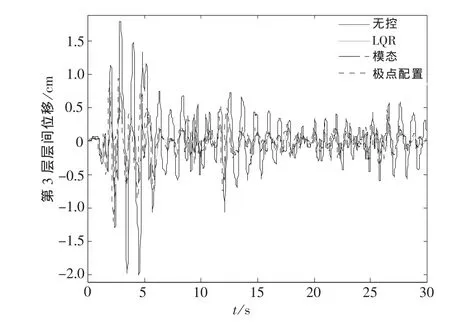
图1　3种主动控制算法和无控时第3层层间位移Fig.1 Three active control algorithms and the third layer displacement without control（ki=7×107N·m-1）

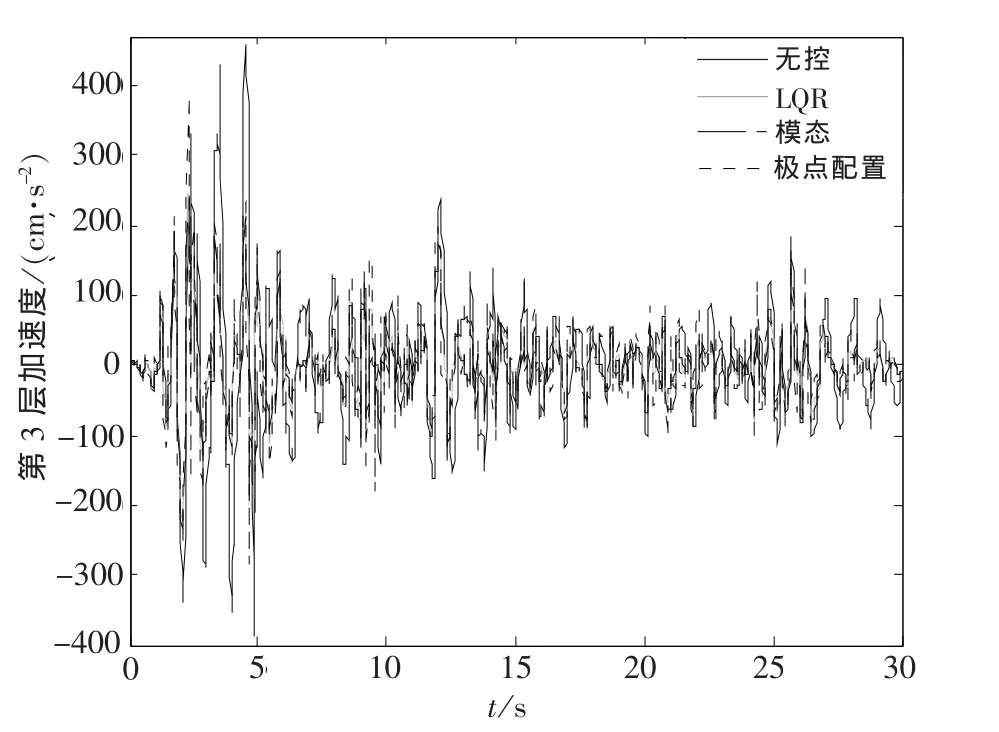
图2　3种主动控制算法和无控时第3层加速度Fig.2 Three active control algorithms and the third layer acceleration without control（ki=7×107N·m-1）

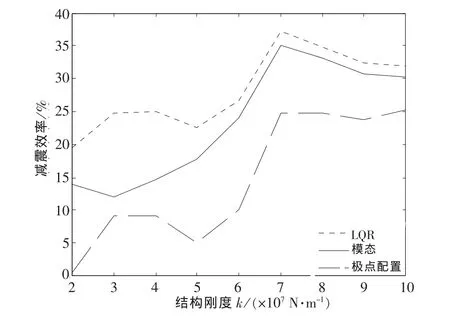
图3　3种主动控制算法对结构总加速度的减震效率Fig.3 Three active control algorithm s on the total acceleration of the structure of the dam ping efficiency

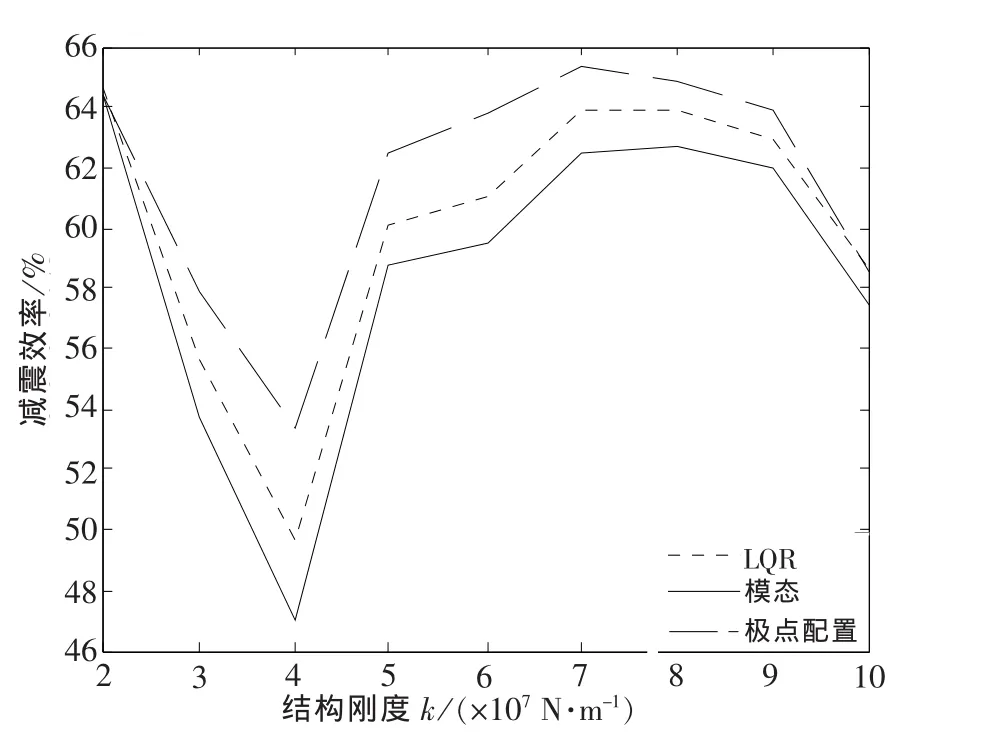
图4　3种主动控制算对结构总位移的减震效率Fig.4 Three active control algorithm s on the total displacement of the structure of the dam ping efficiency

对于刚性结构，可取ki=p×108N／m，p=2，…，10［5］.结构振动响应见图5～图6（只给出结构抗侧刚度ki=7×108N／m时，第3层的位移、加速度，其他层类似），减震效率见图7～图8.从图中可看出，当结构刚度较大时，3种主动控制算法控制效果均较理想，甚至基本一致.

对于柔性结构，可取ki=p×106N／m，p=2，…，10［5］.结构振动响应见图9～图10（只给出结构抗侧刚度ki=7×106N／m时，第3层的位移、加速度，其他层类似），其中极点配置控制算法中极点配置方法按本文式（19）确定，减震效率见图11～图14.

从图9～图14中得出，当结构较柔、刚度较小时，3种控制算法对结构位移响应均具有良好的控制效果，对于加速度响应，LQR控制算法和模态控制算法仍具备一定的控制效果，而极点配置控制算法使结构第3层加速度的减震效率为负值，说明当结构刚度较小时，极点配置控制算法非但不能减小结构地震响应，甚至会放大结构的加速度响应，且总位移减震效率也明显低于其他2种主动控制算法；因此，对柔性结构来说，采用式（19）极点配置方法的极点配置控制算法并不适宜，而对于结构振动控制来说，一般对加速度的控制比对位移的控制更加迫切，此时，极点配置控制算法中采用文献［13］提出的极点优化配置方法，得到适宜的状态反馈增益矩阵，可以显著改善结构加速度响应控制效果，如图15～图16所示.

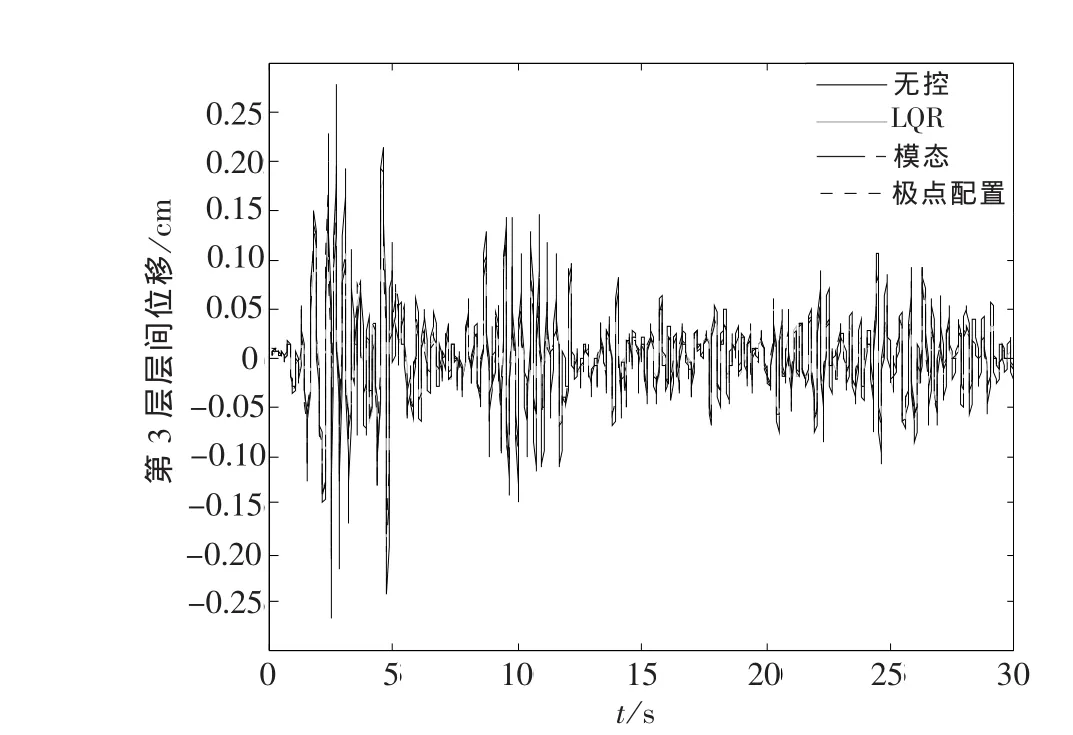
图5　有控和无控时刚性结构第3层层间位移Fig.5 The third layer displacement of rigid structure with control and without control（ki=7×108N·m-1）

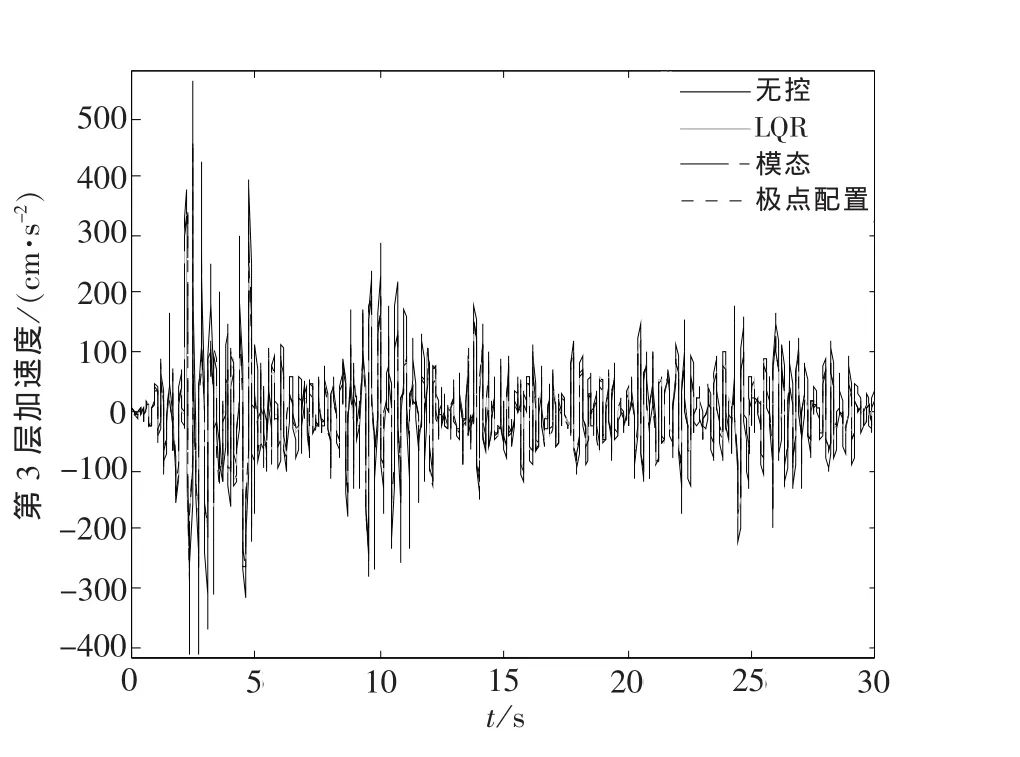
图6　有控和无控时刚性结构第3层加速度Fig.6 The third layer acceleration of rigid structure with control and without control（ki=7×108N·m-1）

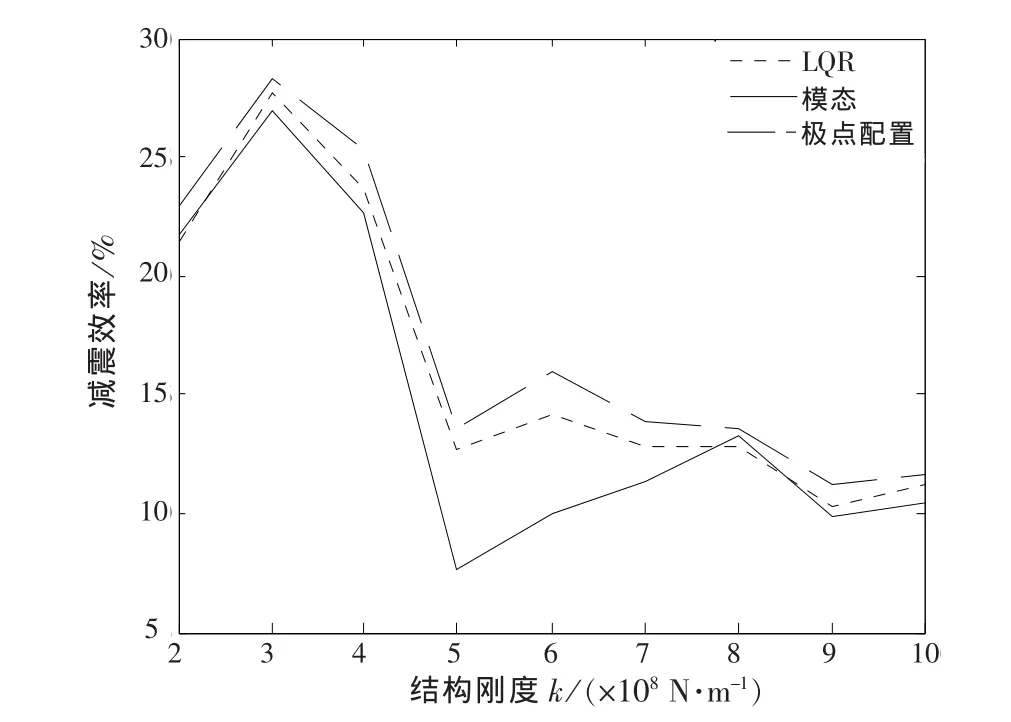
图7　有控时刚性结构总加速度的减震效率Fig.7 Dam ping efficiency of the total acceleration of the rigid structure with control

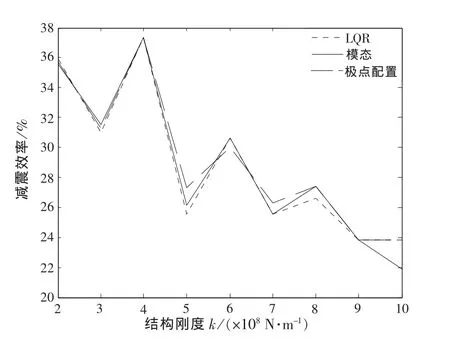
图8　有控时刚性结构总位移的减震效率Fig.8 Dam ping efficiency of the total displacement of the rigid structure with control

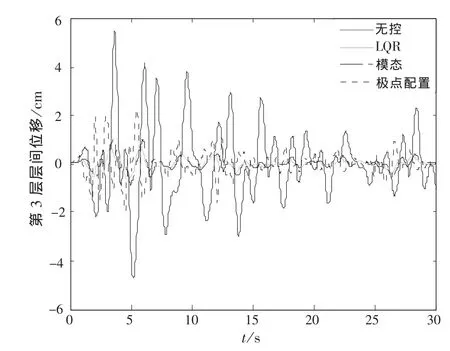
图9　有控和无控时柔性结构第3层层间位移Fig.9 The third layer displacement of flexible structure with control and without control（ki=7×106N·m-1）

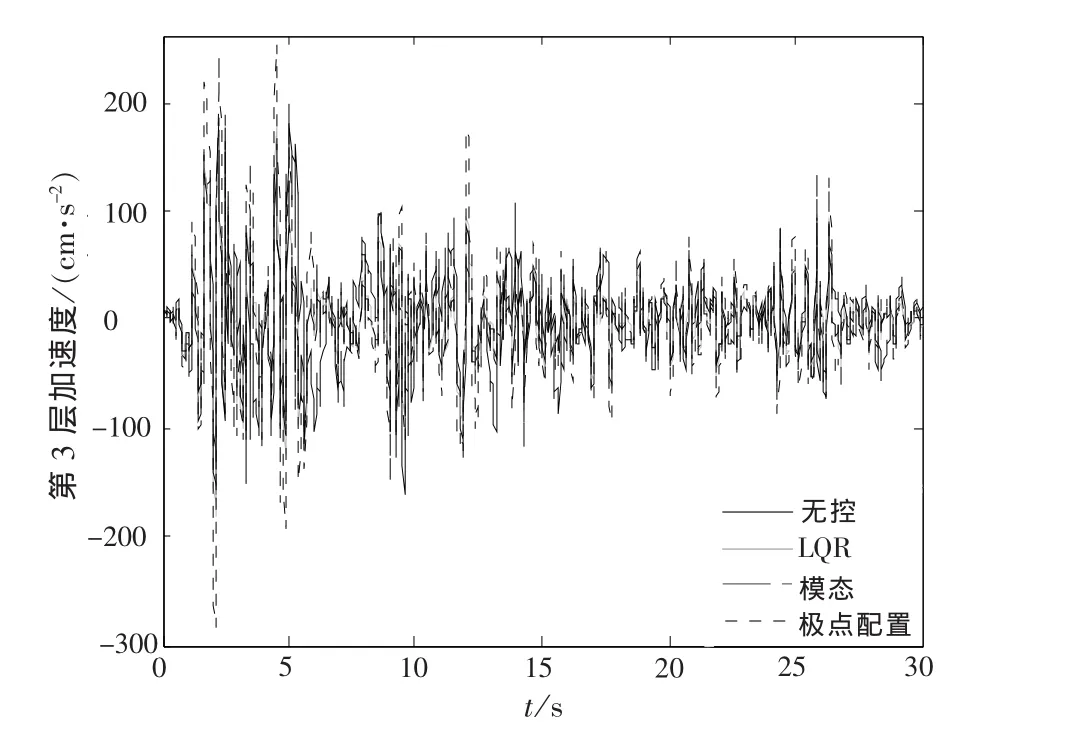
图10　有控和无控时柔性结构第3层加速度Fig.10 The third layer acceleration of rigid structure with control and without control（ki=7×106N·m-1）

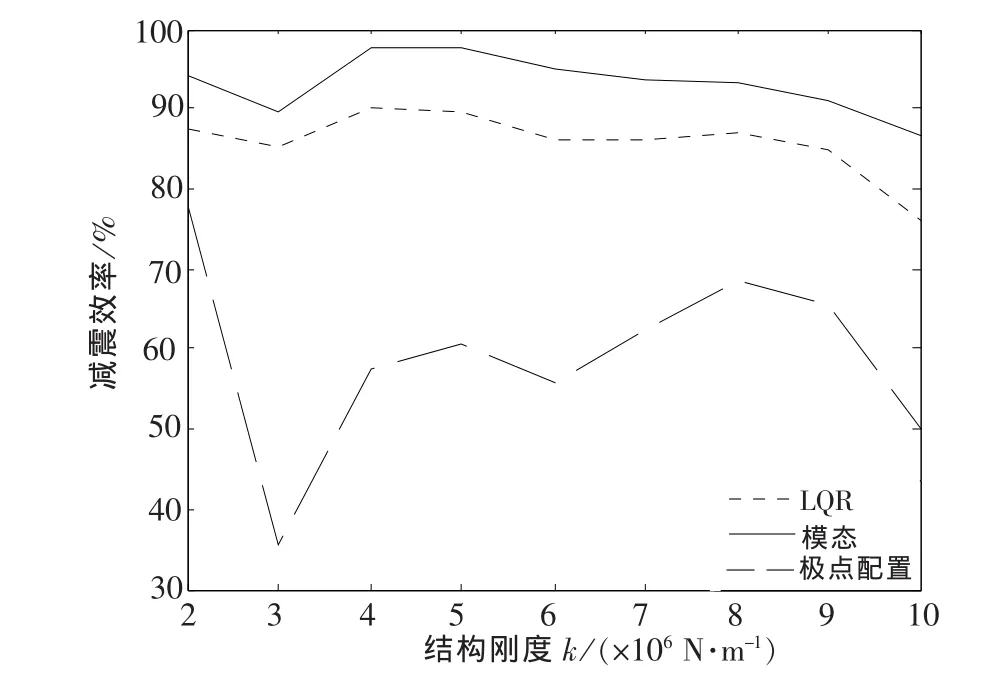
图11　有控时柔性结构第3层层间位移的减震效率Fig.11 Damping efficiency of the third layer displacement of flexible structure with control

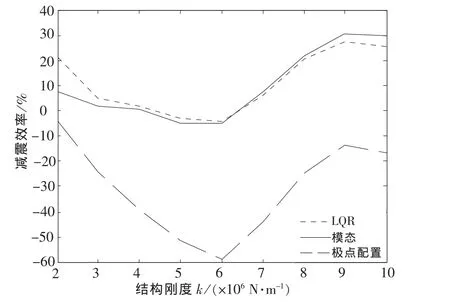
图12　有控时柔性结构第3层加速度的减震效率Fig.12 Damping efficiency of the third layer acceleration of flexible structure with control

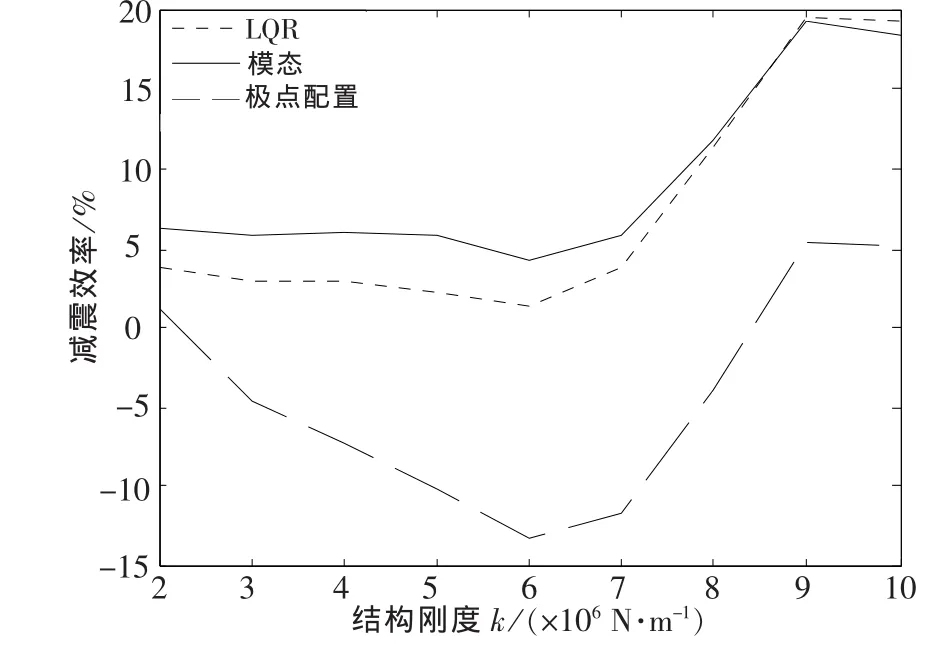
图13　有控时柔性结构总加速度的减震效率Fig.13 Dam ping efficiency of the total acceleration of the flexible structure with control

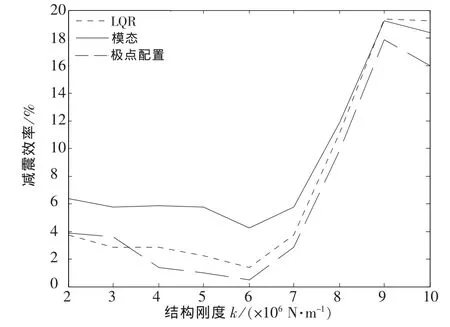
图15　有控时柔性结构总加速度的减震效率Fig.15 Dam ping efficiency of the total acceleration of the flexible structure with control

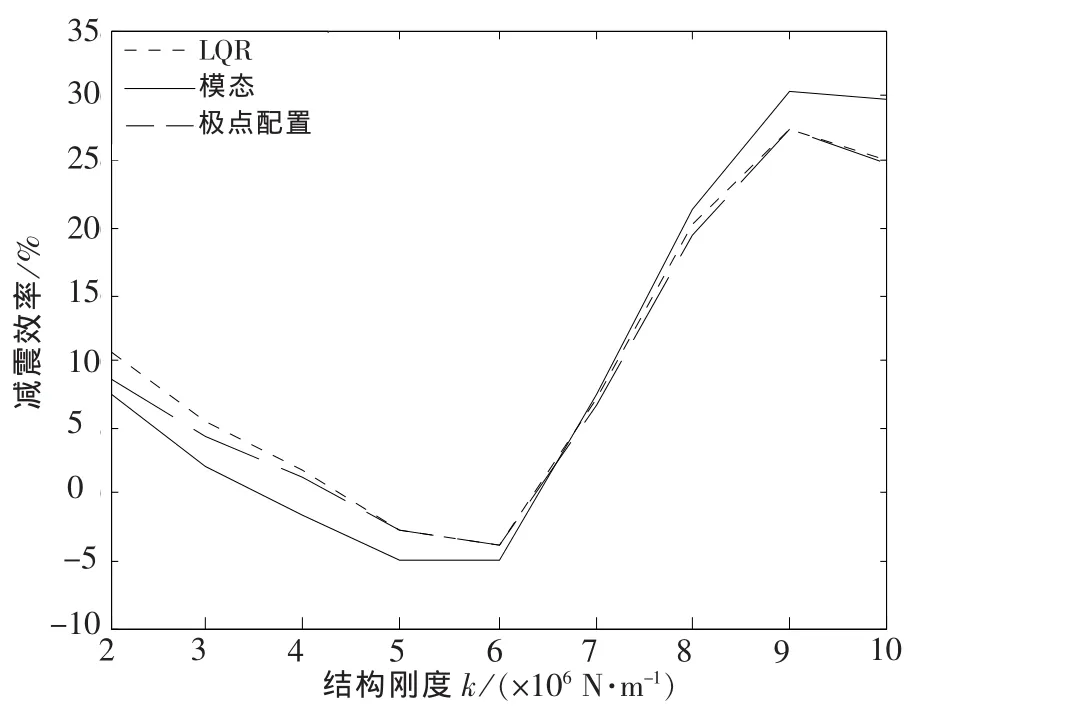
图16　有控时柔性结构第3层加速度的减震效率Fig.16 Damping efficiency of the third layer acceleration of flexible structure with control

6　结论

本文采用3种主动控制算法，计算了结构振动控制系统反应，比较分析了3种主动控制算法的振动控制效果，得到以下结论：

1）主动控制能够有效地减小结构的地震响应，当结构刚度较大时，3种主动控制算法计算的控制效果均较理想，甚至基本一致；

2）当结构刚度较小、为柔性结构时，3种主动控制算法对结构的控制效果并不相同.整体而言，采用LQR控制算法和模态控制算法得到的结构振动响应较小，减震效率较高，控制效果较好，而极点配置控制算法减震效率明显低于其他2种主动控制算法，甚至会放大结构加速度响应，这时需要优化极点配置，以得到适宜的状态反馈增益矩阵，当采用文献［13］所述的极点配置方法时，可以使结构加速度响应控制效果得到显著改善.

［1］PREUMONTA.Vibration Control of Active Structures：A n Introduction［M］.Berlin：Springer Science＆Business Media，2012.

［2］HANSENC，SNYDERS，QIUX，et al.Active Control of Noise and Vibration［M］.Florida：CRC Press，2012.

［3］邱贤波.阻尼器减震结构随机地震响应及等效阻尼比分析［D］.柳州：广西工学院，2012.

［4］葛新广，李创第，陆运军.带悬吊质量摆减振系统的建筑结构随机风振响应的解析解法［J］.广西工学院学报，2009，20（4）：6－10.

［5］欧进萍.结构振动控制——主动、半主动和智能控制［M］.北京：科学出版社，2003.

［6］CASCIATIF，RODELLAR J，YILDIRIM U.Active and Semi－Active Control of Structures-Theory and Applications：A Review of Recent Advances［J］.Journal of Intelligent Material Systems and Structures，2012，23（11）：1181－1195.

［7］张春良.振动主动控制及应用［M］.哈尔滨：哈尔滨工业大学出版社，2011.

［8］KORKMAZS.A Review of Active Structural Control：Challenges for Engineering Informatics［J］.Computers and Structures，2011，89（23）：2113－2132.

［9］EL－KHOURY O，ADELI H.Recent Advances on Vibration Control of Structures under Dynamic Loading［J］.Archives of Computational Methods in Engineering，2013，20（4）：353－360.

［10］侯军芳，李荣利，白鸿柏.主动隔振平台模态区间参数模型的独立模态控制方法［J］.振动工程学报，2011，24（6）：670－675.

［11］MOTTERSHEAD JE，T EHRANI M G，J AMES S，et al.Active Vibration Suppression by Pole－Z ero Placement Using Measured Receptances［J］.Journal of Sound and Vibration，2008，311（3）：1391－1408.

［12］ZHANG J，OUYANG H，YANG J.Partial Eigenstructure Assignment for Undamped Vibration Systems Using Acceleration and Displacement Feedback［J］.Journal of Sound and Vibration，2014，333（1）：1－12.

［13］杜永峰，李春锋，李慧.结构主动控制最优极点配置算法研究［J］.振动与冲击，2012，31（19）：95－98，103.

（学科编辑：黎娅）

Research on the structural vibration control effects of three active control algorithms

FAN Wen-hua,ZOU Wan-jie*
(School of Civil Engineering and Architecture,Guangxi University of Science and Technology, Liuzhou 545006,China)

According to the different types of structure,the corresponding control force state feedback gain matrix is obtained by the correlation function commands in Matlab,then the displacement,acceleration and control force of the structure vibration are obtained,and the control effects of the three active control algorithms are compared.And given a calculation example of three layer frame structure based on Matlab,the results show that the active control can effectively reduce the seismic response of the structure.Especially when the structure stiffness is large,the control effects of the three active control algorithms are ideal.When the structure stiffness is small,the control effects of various control algorithms are relatively large.The control effects of LQR control algorithm and Modal control algorithm are better,and the pole placement algorithm is less effective,and it may even amplify seismic response.In this case,we need to optimize the pole placement to obtain an adequate state feedback gain matrix to improve the structural acceleration control effects.

active control algorithm;structural stiffness;control effect;Matlab

TU31

A

2095-7335（2016）03-0069-07

10.16375/j.cnki.cn45-1395/t.2016.03.013

2015-12-31

广西自然科学基金（2011GXNSFA018032）资助.

＊邹万杰，博士，副教授，研究方向：结构振动控制，E-mail：705450818＠qq.com.