基于听觉模型和极值点概率密度的断齿故障特征提取方法研究
2016-11-23吴文寿李允公李国萌石悦红
吴文寿, 李允公, 王 波, 李国萌, 石悦红
(东北大学 机械工程与自动化学院,沈阳 110819)
基于听觉模型和极值点概率密度的断齿故障特征提取方法研究
吴文寿, 李允公, 王 波, 李国萌, 石悦红
(东北大学 机械工程与自动化学院,沈阳 110819)
齿轮断齿故障的重要特征是啮合过程中在断齿处产生碰撞与冲击。考虑到人耳听觉系统对于突发的瞬态声信号具有本能的反应,为提取断齿故障诱发的瞬态冲击响应成分,提出一种基于听觉模型和信号极值点概率密度的特征提取方法。该方法首先对信号进行GT带通滤波、相位调整及极值点提取,然后计算各极值点的幅值概率密度,通过对其求导判断各滤波通道中是否存在瞬态冲击成分,继而提取与之相关的极值点。同时,由于系统振动时会产生与断齿冲击无关的极值点,为准确提取断齿冲击,根据瞬态信号频带连续性和多频段分布特点,设计了相应的提取方法。经实测信号验证表明,所提方法能准确刻画及提取断齿故障特征,可以在含有多种类型的瞬态冲击响应成分中提取出只由断齿故障所诱发的冲击成分,且提取结果精确度较高。
断齿故障;听觉模型;概率密度;瞬态信号;故障诊断;特征提取
齿轮传动是一种最为常见的传动形式。据统计,在机械设备故障或状态不良的原因中,约60%[1]与齿轮失效有关,而轮齿断裂在齿轮失效形式中所占比例又最高,约为41%[2]。断齿使齿轮副不能正常啮合,并产生周期性冲击响应成分。断齿故障的动力学特性十分丰富[3],但最本质、最能区别于其他齿轮故障特征的在于断齿会诱发出周期性瞬态冲击响应成分[4],且断齿越严重,冲击越明显。因此,如果能提取断齿故障的冲击响应成分,并且能够识别出冲击响应出现的周期,则可对齿轮断齿故障诊断提供有效依据。在瞬态冲击成分提取方面,栗茂林等[5]提出一种对连续小波系数进行非线性化,实现冲击成分特征提取。WANG等[6]提出一种基于Levenberg-Marquardt方法的瞬态模型和参数识别迭代提取方法,并最终应用于轴承和齿轮故障特征提取。严保康等[7]提出一种利用形态提升方法,通过放大微弱冲击成分来实现微冲击特征提取,并成功运用到滚动轴承早期微弱脉冲故障检测中。近年以来,利用谱峭度[8]方法也受到学者深入研究,主要利用谱峭度对瞬态冲击成分较为敏感,依此来发现冲击成分所占据的频段,以便确定滤波器的带宽和中心频率,此方法对于提取瞬态冲击信号表现良好。
人耳听觉系统对突发的瞬态声音信号具有本能的反应[9],基于此,李允公等[10]提出一种基于极值点概率密度和听觉模型的瞬态信号提取方法,该方法从瞬态信号导致的概率密度曲线的长拖尾现象出发,并结合听觉模型提出相应的存在瞬态信号判断方法。此方法提取的瞬态信号起始时间的准确性较高,且当背景信号或干扰噪声较强时也可获得满意效果,但未考虑在对不同类型瞬态信号的区分。
考虑到即使在正常的齿轮系统中也有可能产生瞬态振动成分(如轻载时侧隙过大),为提取只与断齿有关的瞬态冲击成分,本文基于听觉模型和信号极值点幅值概率密度,提出了专门针对由断齿故障所诱发的冲击成分提取方法。经实验验证表明该方法能很好的提取仅与断齿故障相关的冲击响应成分,并且能够识别冲击响应出现的周期。
1 方法概述
1.1 基本原理
本文所提方法的实现过程如图1所示,首先利用Gammatone滤波器组对信号进行带通滤波,为消除滤波时出现的相位不一致,对滤波之后的结果再采用逆序滤波,然后计算各滤波通道内幅值极大值点的概率密度及其导数。根据处理结果判断是否存在瞬态冲击成分,继而筛选有效幅值极值点并进行区分提取,最终提取得到只含有断齿故障的瞬态信号成分。

图1 方法实现过程原理图Fig.1 The principle diagram of the method implementation process
1.2 Gammatone滤波器
Gammatone滤波器组[11]是通过模拟人耳耳蜗基底膜的滤波特性所提出的一种带通滤波方法。设振动信号为x(t),共有N个滤波器,则第i个滤波器的冲击响应表达式为
h(i,t)=Bntn-1exp(-2πBt)cos(2πfit+φi)
(1)
式中:n为滤波器阶数;φi为相位;fi为第i个滤波器的中心频率。
参数B与fi的关系为:
B=1.019×ERB(fi)=1.019(24.7+0.108fi)
(2)
式中:ERB(fi)为Gammatone滤波器的等效矩形带宽。
滤波器的时域波形如图2所示。

图2 滤波器时域波形Fig.2 The filter waveform in time domain
则带通滤波为
y(i,t)=x(t)*h(i,t)
(3)
式中:*代表卷积。
为避免同一频率成分在不同滤波通道中出现相位差异,在基于傅里叶变换进行卷积运算时忽略滤波器h(i,t)的相频特性,实现逆序滤波,即
(4)
式中:F-1表示傅里叶逆变换,X(f)和H(i,f)分别为x(t)和h(i,t)的频域表达。
随后对逆序滤波之后的信号提取所有极大值点,其余幅值均置为零,得到y1(i,t)。
本文选择200个Gammatone滤波器来实现带通滤波,滤波器中心频率通常按照对数均匀分布设置,图3为不同中心频率下滤波器的频谱图(图中只绘出16个滤波器)。
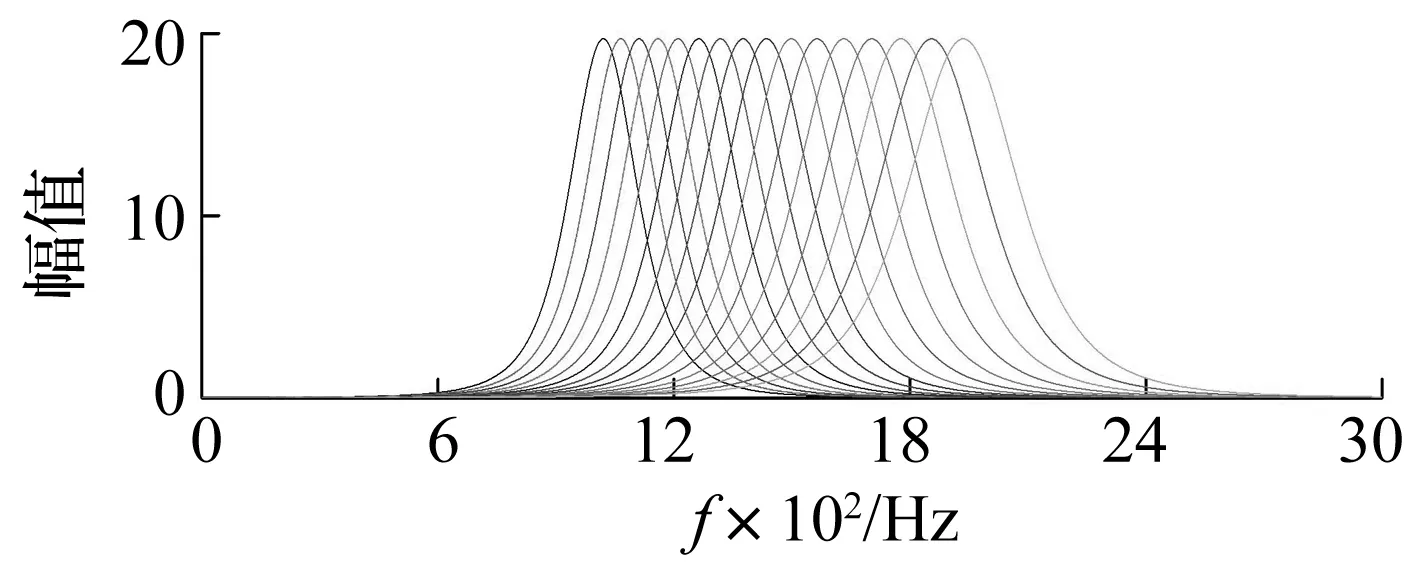
图3 滤波器频谱图Fig.3 The spectrum of filter
1.3 瞬态信号识别方法
若机械系统中存在碰撞与冲击,一般情况下,其振动信号中会存在幅值明显的瞬态冲击响应成分,信号的概率密度曲线也必然会出现如图4所示的长拖尾现象[8]。
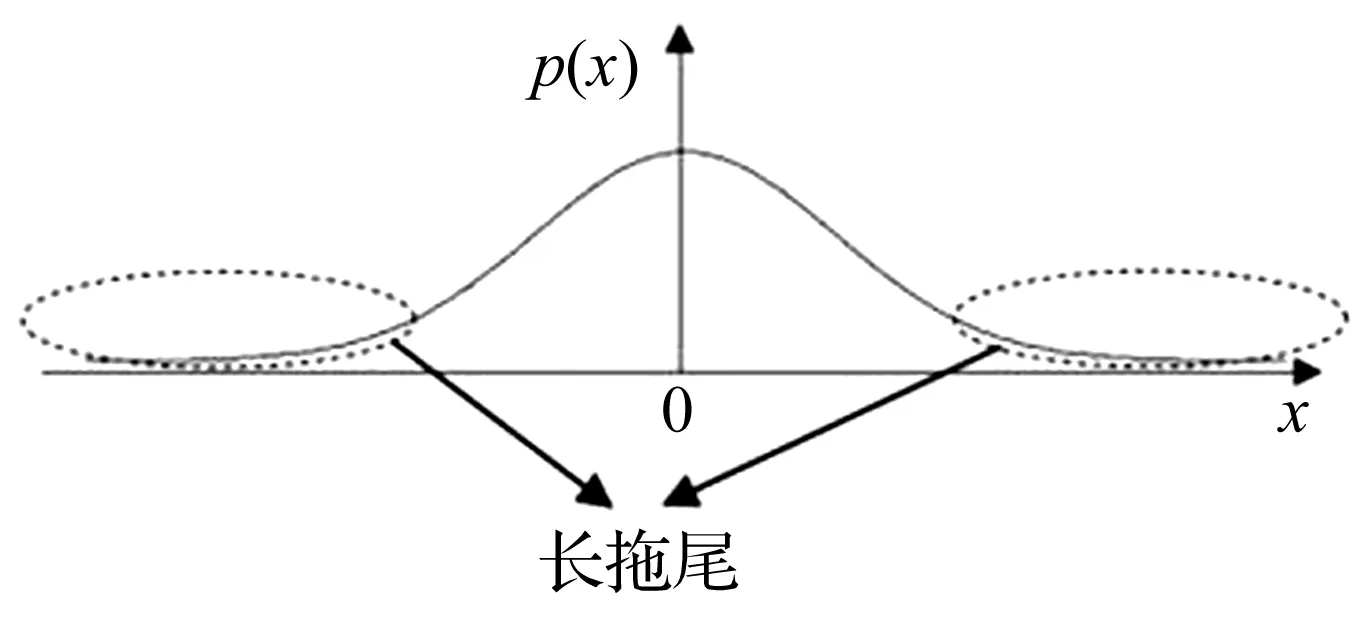
图4 瞬态信号所致概率密度曲线的长拖尾现象Fig.4 Heavy-tailed in probability densitycurve induced by transient signal
但是仅依据长拖尾部分难以判断瞬态信号的幅值范围,因此,可提取信号的极大值点,并计算极大值点的概率密度曲线p(i,g)。由于极值点幅值间往往具有较强的不连续性,所以在极值点的幅值概率密度曲线中的长拖尾部分会出现小幅值波动情况,而且这部分的幅值必然与瞬态冲击成分有关,基于此特点,为实现对瞬态成分的自动识别,计算p(i,g)关于g的导数
(5)
式中:g表示逆序滤波之后信号幅值的极大值点。
利用d(i,g)曲线,按以下准则[10]判断第i通道里是否含有瞬态冲击成分:
① 在d(i,g)曲线经历最小值之后,存在向上过零点,记该点的横坐标为g0。
②ηq为一个小值,且
(6)
式中:θ是预先给定的阈值,本文取θ=0.1。
1.4 瞬态信号筛选提取
依据上述两条判断准则,可初步提取与瞬态冲击成分相关的极值点,若d(i,g)满足以上准则,则令:
(7)
式中:幅值为1的位置很可能为瞬态冲击信号的极值点。
为使初步提取的极值点连续化,并形成波形,可将y2(i,t)和一方波信号做卷积得到y3(i,t),即
y3(i,t)=y2(i,t)*r(t)
(8)
式中:r(t)表示方波信号。
由于信号在经时频分解之后,瞬态冲击成分会占据一定的连续频带,且在某些频率处达到峰值。为使冲击成分辨识更加突出明显,将y3(i,t)沿各通道方向累加求和得到θ1(t),即
(9)
此外,为明确冲击成分的频域分布情况,将y3(i,t)沿着时间方向累加求和得到θ2(i),即
(10)
继而计算Ω(i,t),即
Ω(i,t)=θ1(t)θ2(i)
(11)
可知,若Ω(i,t)非零,则说明在第i通道、t时刻时存在瞬态冲击成分。
为了进一步将y3(i,t)中无关的极值点删除,使其达到简炼的目的,继而计算z(i,t),即
z(i,t)=y3(i,t)Ω(i,t)
(12)
1.5 断齿瞬态信号区分提取
由于轮齿间啮合拍打、存在侧隙或轴承出现小故障,均会引起瞬态冲击成分,但是其往往高频部分能量较小,且占据的频带较窄,这也意味着会出现与断齿故障无关的极值点。
而断齿导致的冲击响应成分往往能量较大,且会占据较宽的频段。因此,为将淹没在其中的断齿冲击响应成分准确提取,对z(i,t)进行分频段统计,平均分为α个频段依次累加分别得到s1(t)、s2(t)、s3(t),…,sα(t),即
(13)
(14)
(15)
⋮
(16)
式中:ν=N/α,N为滤波器个数。
将sk(t)(k=1,2,3,…,α)两两相乘得到alp(t),即
alp(t)=sl(t)sp(t)(l,p=1,2,3,…,αl≠p)
(17)
按图5所示的流程原则比较有值区域和无值区域,通过选取sk(t)和alp(t)来获取提取结果。
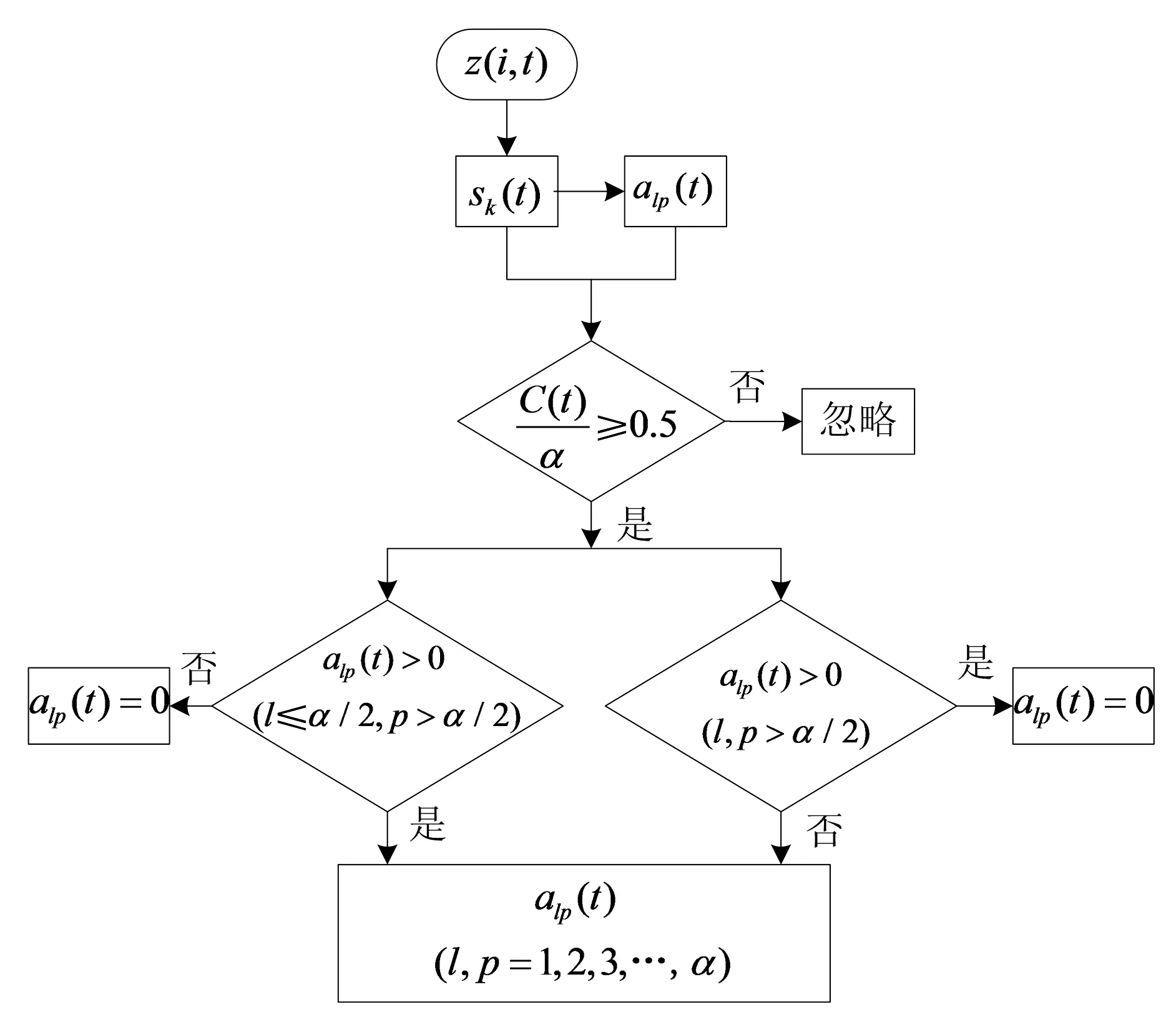
图5 sk(t),alp(t)选择流程图Fig.5 Selection flow chart of sk(t) and alp(t)
图5中
C(t)=count{sk(t)>0,k=1,2,3,…,α}
(18)
表示当在t时刻时,若第k个频段上满足sk(t)>0,则计为1,否则为零,各频段依次将结果累加为C(t)。
继而用alp(t)分别和含有瞬态冲击成分的滤波信号相乘之后再累加求和得到Tq,即
(19)
最终,Tq(t)即为提取出的只含有由断齿所引发的瞬态冲击响应成分。
2 实验验证
为验证本文所提方法在齿轮断齿故障特征提取中的有效性,搭建如图6所示的二级斜齿圆柱齿轮减速器实验台及人为断齿故障,其主要零部件参数为:电动机额定功率750 W,最大转速1 400 r/min;减速器高低速级齿数分别为13,86,14,85;选用压电式加速度传感器拾取振动信号,考虑到冲击成分会激发各阶固有频率,且其固有频率往往较高,为满足采样定理且提高信号的还原度,设置采样频率为10 240 Hz。

图6 减速器实验台和人为齿轮断齿故障Fig.6 Redactor test rig and artificial gear fracture fault
测得减速器高速轴转速为937 r/min,理论计算旋转频率fr=15.62 Hz,啮合频率fm=203.3 Hz,图7为断齿故障的振动加速度信号时域波形图和频谱图。在时域波形图中虽然可以明显看出存在瞬态冲击成分,但难以分辨出断齿故障特征;频谱图中虽然存在旋转频率和啮合频率及其高次倍频,但谱线过于密集,不能准确判断出是何故障。
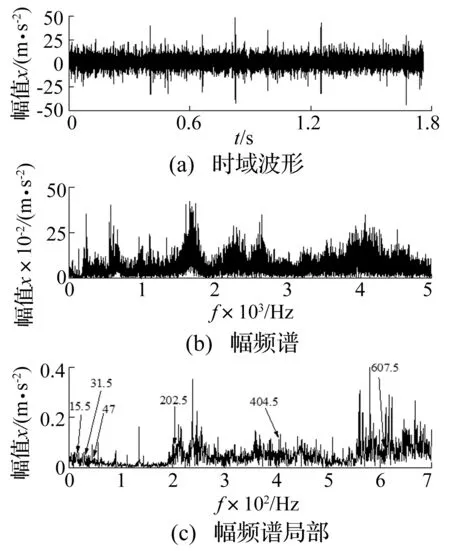
图7 齿轮断齿故障信号时域波形及其频谱Fig.7 Time waveform and frequency spectrum of gear fracture fault
滤波器参数选择如下:滤波器个数N=200;滤波器阶数n=4;相位φi=0;中心频率fi按照对数均匀分布设置。图8是经过逆GT之后的时频图,从此图中也难以辨识瞬态冲击成分。
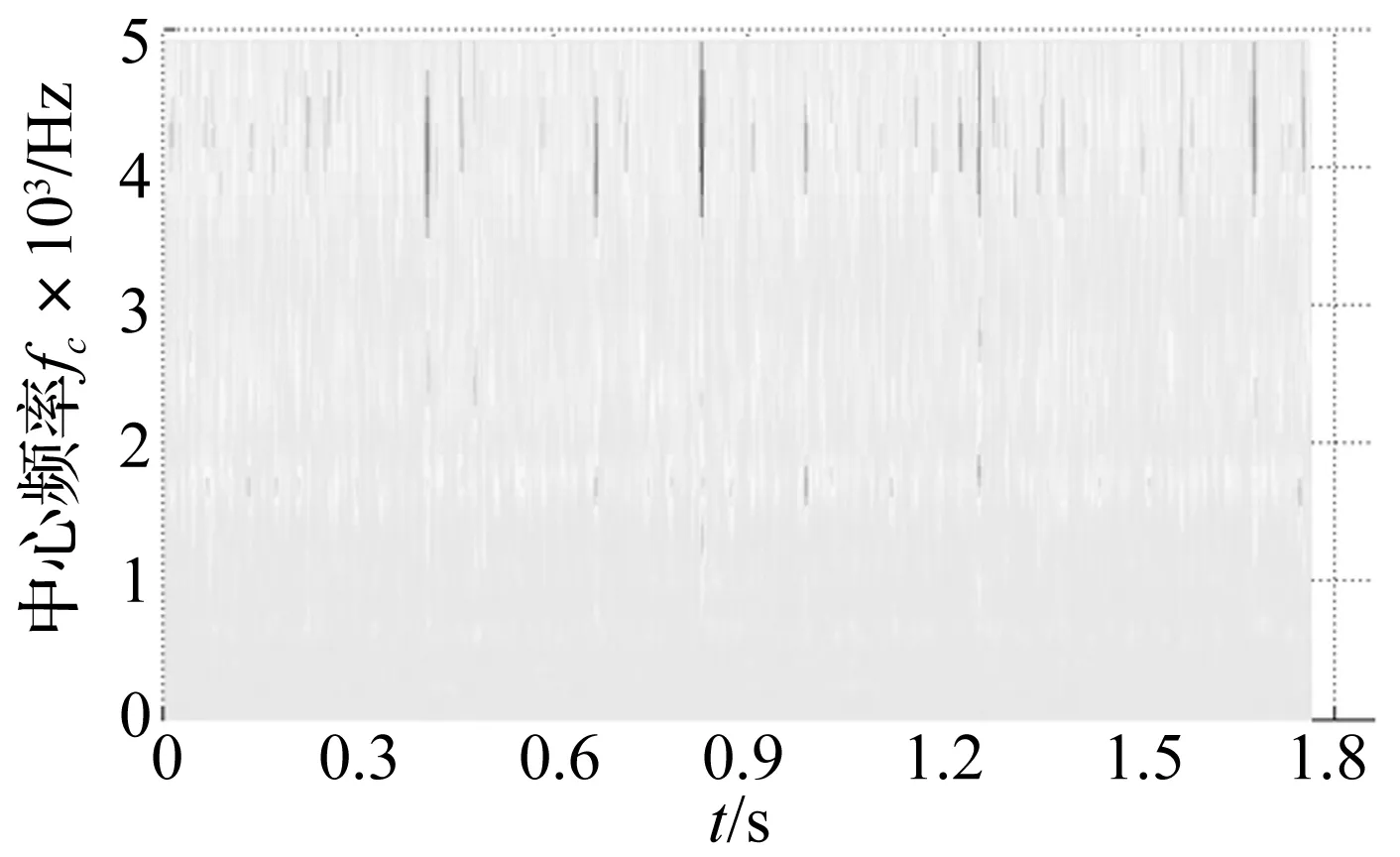
图8 逆GT滤波结果Fig.8 Filtering results of the inverse GT
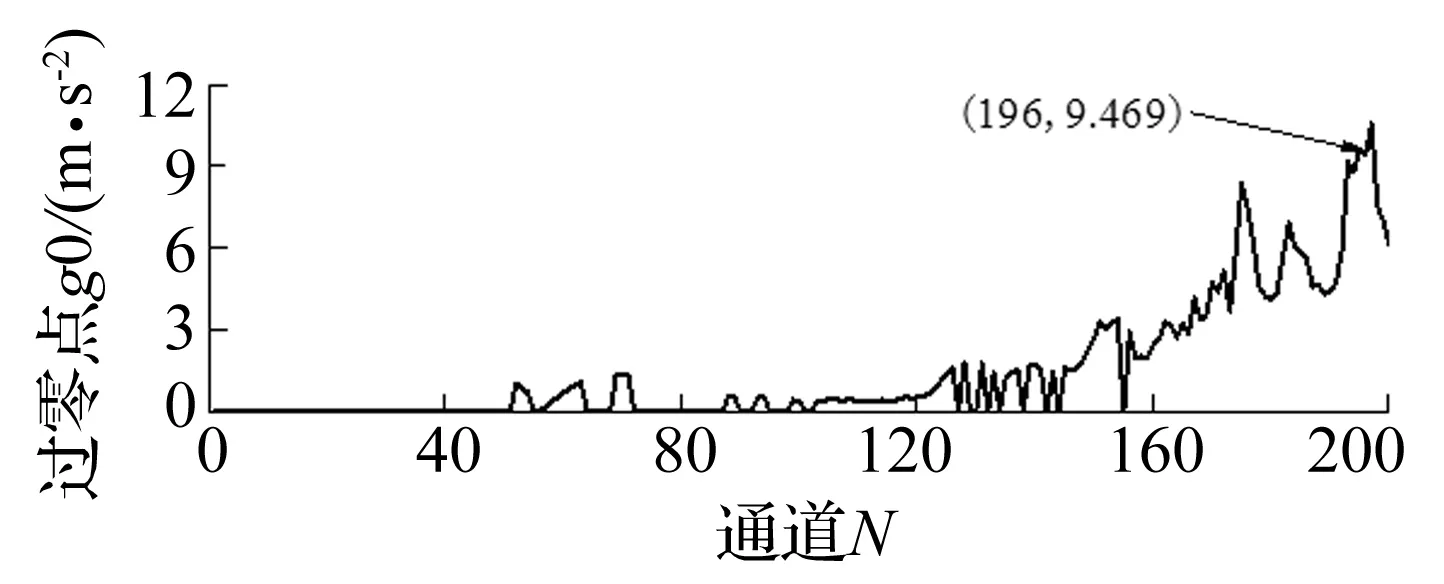
图9 各通道过零点Fig.9 Zero-crossing of each channel
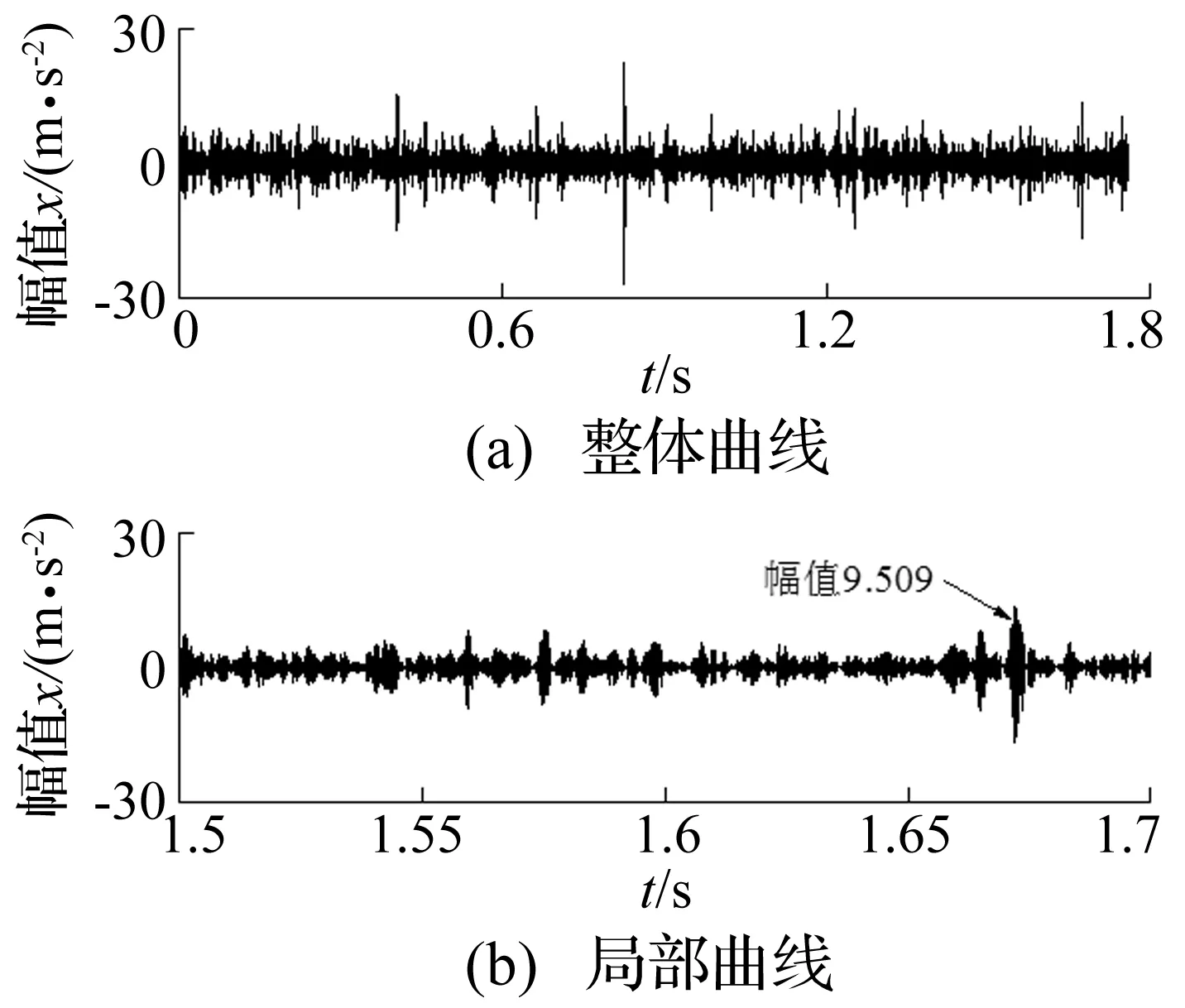
图10 第196通道滤波结果Fig.10 The 196th channel’s filtering results
依据给定的两条判断准则判断筛选后,各通道与其对应的过零点g0对应关系如图9所示,其中幅值为零表示该通道无向上的过零点,即表明无瞬态冲击成分。
以第196通道为例说明。图10是振动信号经逆GT滤波之后的滤波结果及局部放大图,在图10(b)中所指幅值为9.509。
第196通道的概率密度曲线p(g)及其导数d(g)如图11和图12所示,从11(b)中看出p(g)的长拖尾部分出现小幅值波动,且在第三个波峰处幅值为9.469。在12(b)中,g0=9.469是d(196,g)经最小值之后逐渐上升且由负变正的第一个幅值点,并且绝大多数冲击成分的极值点的幅值都会大于g0点,依此便可确定此通道的瞬态冲击信号的幅值范围。
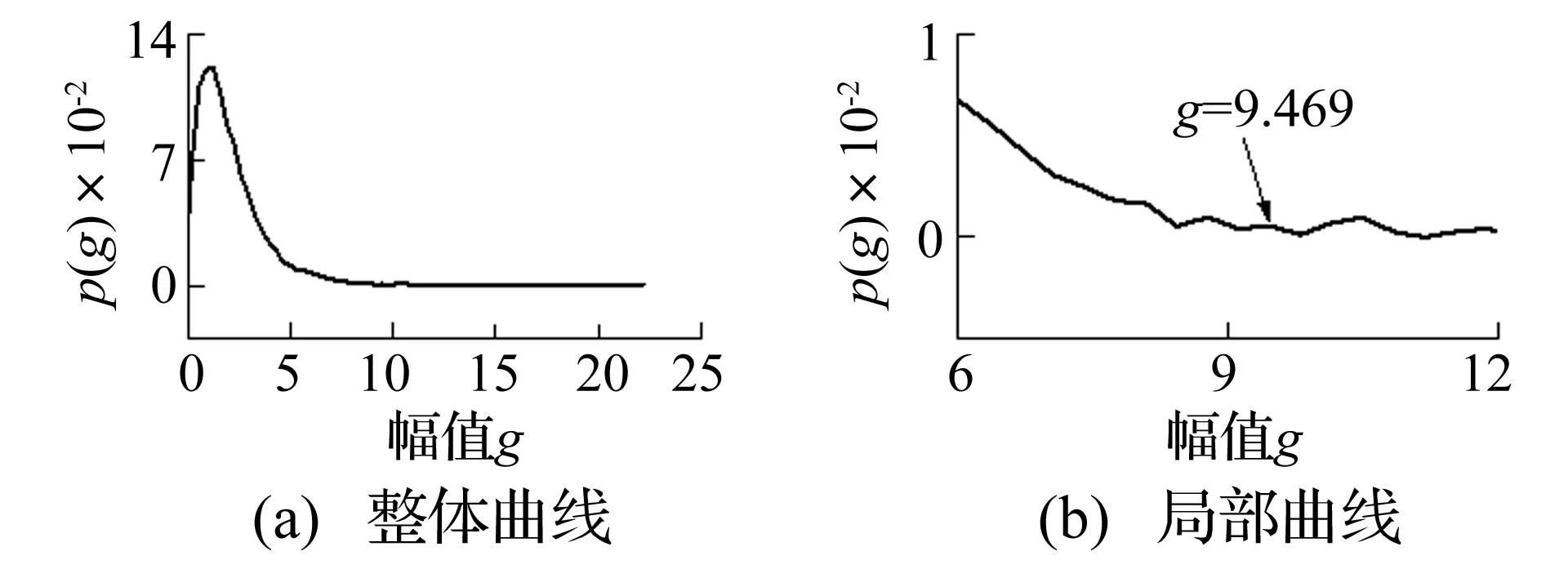
图11 第196通道概率密度曲线Fig.11 The 196th channel’s probability density curve
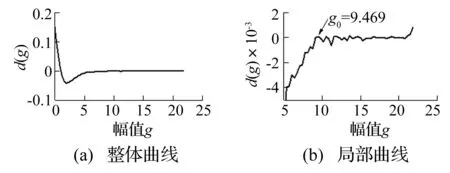
图12 第196通道概率密度曲线的导数Fig.12 The 196th channel’s derivative of probability density
在10 (b)中幅值为9.509的极大值点与图12 (b)的第一个过零点g0点相对应。继而根据上述理论依据,计算θ1(t)、θ2(t)如图13所示,从图13 (a)中已明显的看出周期性瞬态冲击成分,但依然有其他冲击成分。
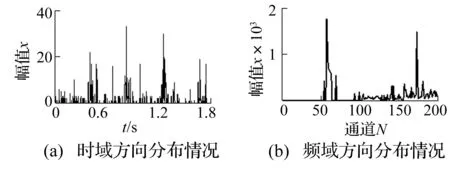
图13 各通道累加结果Fig.13 Accumulative results of each channel
4个不同频段的sk(t)(k=1,2,3,4)分布情况如图14所示。由图可知低频段s1(t)为零,中低频段s2(t)已出现明显的周期性,且有值区域均与高频段s4(t)相对应。为此,经sk(t)两两相乘得到alp(t)如图15所示,因s1(t)为零,图中只给出a23(t)、a24(t)、a34(t)的分布情况。
经流程原则选择筛选后,a24(t)=s2(t)s4(t)即为最终保留的筛选结果,最终提取波形如图16(a)所示,从图中可以看出其周期性非常明显,每两个冲击之间的平均时间间隔为Δt=0.422 4 s,经计算得中间轴转速r=2.360 6 r/s,亦即中间轴大齿轮每转一圈耗时为0.423 6 s,和提取的瞬态冲击时间间隔相一致,从而表明系统发生断齿故障,且发生在中间轴的大齿轮上,与人为制造的断齿位置相匹配。
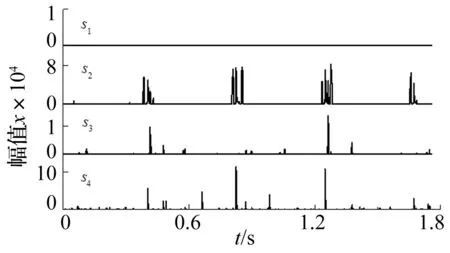
图14 不同频段sk(t)图Fig.14 sk(t) diagram in different frequency bands
图16(b)是提取结果的局部放大图。从图中可以看出,在经一次啮合过程中出现两次冲击(啮入啮出各一次),对于其余三个啮合碰撞也出现同样的结果,并且在图16(c)所示的实测信号的对应位置波形振动趋势和提取结果局部放大图相一致。
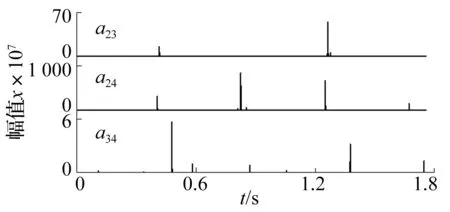
图15 alp(t)图Fig.15 alp(t) diagram
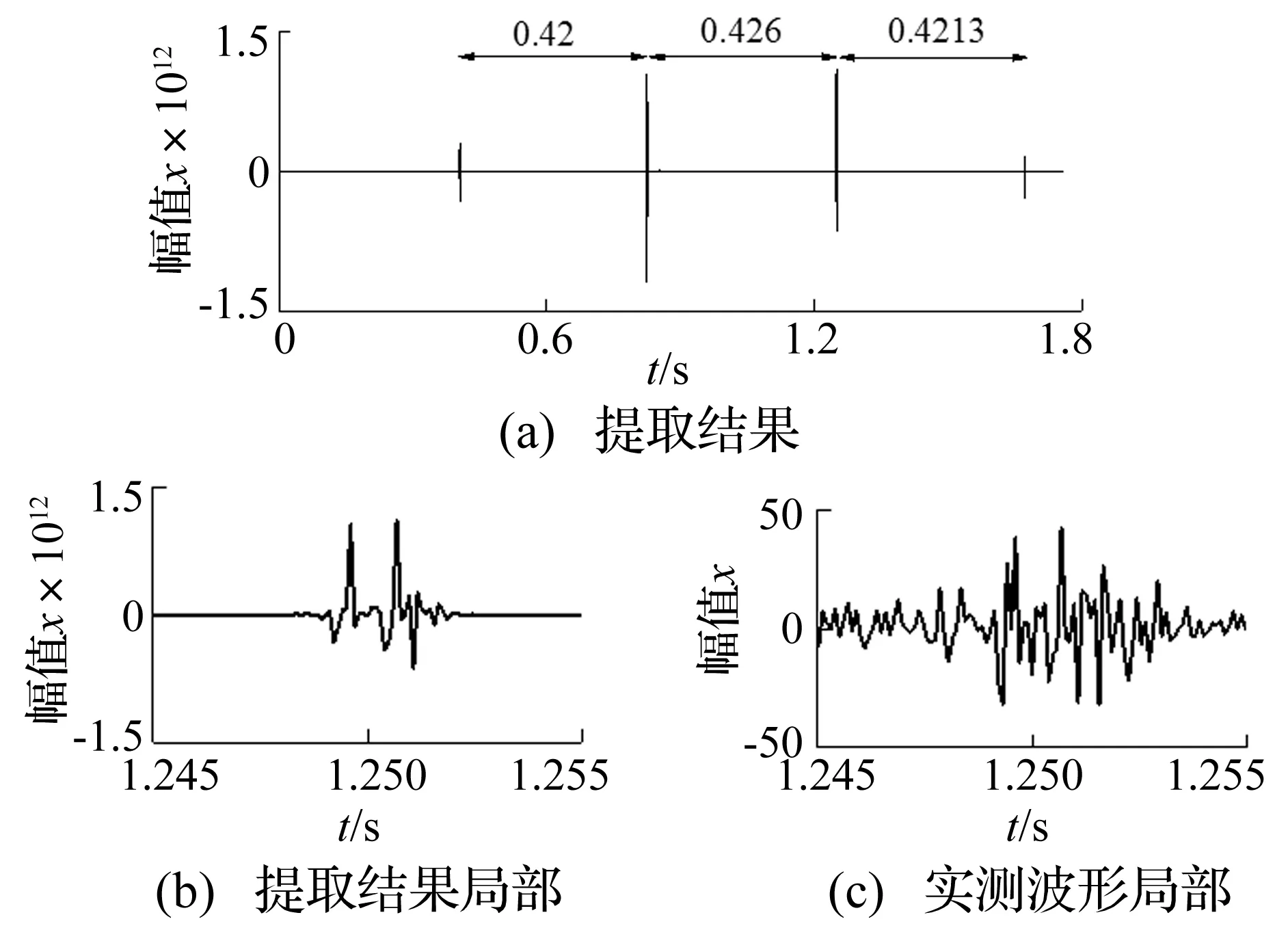
图16 最终信号提取结果Fig.16 Final signal extraction result
3 结 论
本文基于听觉模型和极值点概率密度,提出了一种针对断齿故障特征的提取方法,试验验证结果表明:
(1) 极值点概率密度经求导后,利用其是否存在向上过零点即可自适应的明确各滤波通道中是否存在瞬态成分及其对应的幅值范围。
(2) 该方法能够将断齿故障所诱发的瞬态冲击成分与其他无关冲击相区分,只提取与断齿有关的冲击响应成分,且提取结果便于人和计算机识别,为设备断齿故障检测带来便捷。
(3) 轮齿啮合过程中,在断齿处会产生两次冲击,可作为断齿故障的又一特征。
[1] 唐贵基,庞尔军,王晓龙. 基于EMD的齿轮箱齿轮故诊断的研究[J]. 机床与液压,2013,41(13):188-190.
TANG Guiji,PANG Erjun,WANG Xiaolong. Research on gear fault diagnosis based on EMD[J]. Mchine Tool & Hydraulics,2013,41(13):188-190.
[2] 冯伟. 基于振动分析的齿轮断齿故障研究[J]. 广州航海:高等专科学校学报,2007,15(1):13-16.
FENG Wei. Investigation on gear fracture failure based on vibration analysis[J]. Journal of Guang Zhou Maritime College,2007,15(1):13-16.
[3] 马锐,陈予恕. 齿轮传动系统断齿故障的机理研究[J]. 振动与冲击,2013,32(21):47-51.
MA Rui,CHEN Yushu. Fault mechanism of a gear system with tooth broken[J]. Journal of Vibration and Shock,2013,32(21):47-51.
[4] JENA D P,SAHOO S,PANIGRAHI S N. Gear fault diagnosis using active noise cancellation and adaptive wavelet transform[J]. Measurement,2014,47:356-372.
[5] 栗茂林,梁霖,王孙安,等. 基于连续小波系数非线性流形 学习的冲击特征提取方法[J].振动与冲击,2012,31(1):106-111.
LI Maolin,LIANG Lin,WANG Sunan,et al. Mechanical impact feature extraction method based on nonlinear manifold learning of continuous wavelet coefficients[J]. Journal of Vibration and Shock,2012,31(1):106-111.
[6] WANG Shibin,CAI Gaigai,ZHU Zhongkui,et al. Transient signal analysis based on Levenberg-Marquardt method for fault feature extraction of rotating machines [J]. Mechanical Systems and Signal Processing,2015,54(55):16-40.
[7] 严保康,周凤星. 一种基于形态提升的自适应轴承微冲击提 取方法[J]. 振动与冲击,2013,32(24):198-203.
YAN Baokang,ZHOU Fengxing. Adaptive weak impulse extraction method of rolling bearings based on morphological lifting wavelet[J]. Journal of Vibration and Shock,2013,32(24):198-203.
[8] GUO W,TSE P W,Djordjevich A. Faulty bearing singnal recovery from large noise using a hybrid method based on spectral kurtosis and ensemble empirical mode decomposition [J]. Measurement,2012,45:1308-1322.
[9] KAYA E M,ELHILALI M. A temporal saliency map for modeling auditoryattention [C]//46th Annual Conference on Information Sciences and Systems. Princeton:IEEE,2012:1-6.
[10] 李允公,张金萍,戴丽. 基于极值点概率密度和听觉模型的瞬态信号提取方法研究[J]. 振动与冲击,2015,34(21):37-53.
LI Yungong,ZHANG Jinping,DAI Li. A method extracting transient signals based on probability density of extreme points and on auditory model[J]. Journal of Vibration and Shock,2015,34(21):37-53.
[11] LI Yungong,ZHANG Jinping,DAI Li,et al. Auditory-model-based feature extraction method for mechanical faults diagnosis[J]. Chinese Journal of Mechanical Engineering,2010,21(3):391-397.
A method extracting fault features of gear teeth fractures based on an auditory modeland probability density of extreme points
WU Wenshou, LI Yungong, WANG Bo, LI Guomeng, SHI Yuehong
(School of Mechanical Engineering & Automation,Northeastern University,Shenyang 110819,China)
The collision and impact at gear teeth fractures are the most important features in meshing process of gear pairs. Considering a human auditory system has an instinctive response to sudden transient acoustic signals, in order to extract transient impulse response components induced by gear teeth fracture faults, a method extracting fault features of gear teeth fractures based on an auditory model and signal probability density of extreme points was proposed. Firstly, band-pass filtering with Gammatone filters , phase adjustment and extreme points extraction for signals were conducted, and then the amplitude probability densities of extreme points were calculated, their derivatives were used to judge if there are transient impact components in all filtered signals. Those extreme points with transient impact components were extracted. Meanwhile, the whole system vibration might produce extreme points being irrelevant to gear teeth fracture impacts. In order to accurately extract impacts of gear teeth fractures, according to transient signals’ frequency band continuity and multi-band distribution characteristics, an appropriate extraction method was designed. The real measured signals showed that the proposed method can accurately extract fault features of gear teeth fractures, and can extract impact components only induced by gear teeth fracture faults in a variety of transient impulse response components, and the extraction accuracy is higher.
gear teeth fracture fault; auditory model; probability density; transient signals; fault diagnosis; feature extraction
国家自然科学基金资助项目(51275080)
2015-12-31 修改稿收到日期:2016-03-04
吴文寿 男,硕士生,1991年生
李允公 男,博士,副教授,1976年生
TH17
A
10.13465/j.cnki.jvs.2016.19.017
