海上风电预应力锚杆笼基础结构设计方法研究

王海军，蒋杏雨

(天津大学建筑工程学院，天津300072)



海上风电预应力锚杆笼基础结构设计方法研究

王海军，蒋杏雨

(天津大学建筑工程学院，天津300072)

针对海上风电机组基础承台结构中的锚杆笼新型结构，运用相应的力学方法，提出并改进了对法兰、灌浆层、承台和锚固底板的理论计算方法，并采用有限元仿真模拟计算对理论计算进行了对比验证。结果表明，提出的理论计算方法能够较为准确地计算法兰、灌浆层及承台的应力；对锚固底板，相较于以往经验提出的固结梁和悬臂梁的计算方法，采用弹性地基梁计算方法更接近实际的应力；同时也研究了锚固底板尺寸对底板本身、法兰及灌浆层应力影响，优化了锚固板尺寸，为实际工程提供了参考。

海上风电；预应力锚杆笼基础；设计方法；仿真模拟；锚固底板

海上风电基础形式中，多桩承台和重力式基础是两种常见的基础形式。其中预埋在混凝土结构之中与风机塔筒连接构件的设计对整个基础结构的安全性起到了至关重要的作用。对于连接构件，既要考虑到与上部风机的合理连接，又要考虑到与下部结构结合的安全性[1，2]。在国内外实际工程中，金属基础环结构得到了广泛的应用，而锚杆笼结构相对应用较少。锚杆笼结构与金属基础环结构相比，能够减少混凝土和钢材的用量，锚栓受拉时受力均匀，避免了基础环与混凝土交线处应力集中的不利状况。基于这些优点，这种结构和预应力锚杆笼结构已经被运用到实际工程中[3]。锚杆笼结构源自套管-锚板地脚螺栓型式[4]，在风电基础的使用中是一种较新颖的形式。在先前的研究中，郭敏等[5]提出了一种简便的预应力锚杆笼的理论计算方法，对锚固底板只提出计算思路，并没有明确提出计算公式。而对于风电机组的预应力锚杆，从预紧状态到工作状态，外载荷存在一个载荷分配的过程，并非一成不变[6]。因此在理论计算上还需要进一步研究。另外，有很多尚待优化的结构设计和影响因素也没有考虑到其中，比如锚固底板的宽度、灌浆层的材料性质等，都会对整个结构安全性造成一定的影响。

针对以上存在的问题，本文以材料力学方法推导了预应力锚杆笼基础的法兰、灌浆层、承台、锚固底板的应力计算公式，并结合工程采用ABAQUS软件建立了三维有限元模型进行受力分析，验证了推导公式的合理性。此外，还探究了在固定荷载的条件下，锚固底板尺寸对过渡段等结构的受力影响。

1 预应力锚杆笼结构应力计算

锚杆笼结构主要由T形法兰、预应力锚杆和锚固底板三部分组成，如图1所示。预应力锚杆为风电机组提供固定上部塔筒的预紧力，在上部与T形法兰相连接，下部由锚固底板固定在基础混凝土中，灌浆层的作用则是进行二次灌浆，对锚杆笼起加固作用。与基础环结构不同，锚杆笼结构由多个部分共同构成，因此每个部分受力和传力特性需要保证。在设计中锚杆笼关键的参数为：T形法兰的受力、灌浆层的应力、承台表面压力、锚杆应力和锚固底板的应力[5]。

图1 预应力锚杆笼结构示意

1.1 法兰的最大弯曲应力

风电基础是一个对称结构，与塔筒通过T形法兰连接。在理论计算中假定该过渡段的转动中心在T形法兰的底部中心，如图2(图1的1- 1剖面)所示。由材料力学方法[7]可以推导出弯矩M及塔筒传导自上而下的竖向力Fv作用下，法兰面应力σ1及σ2，即

(1)

式中，D为过渡段壁的中心直径；δ为过渡段壁厚；I为截面贯性矩。

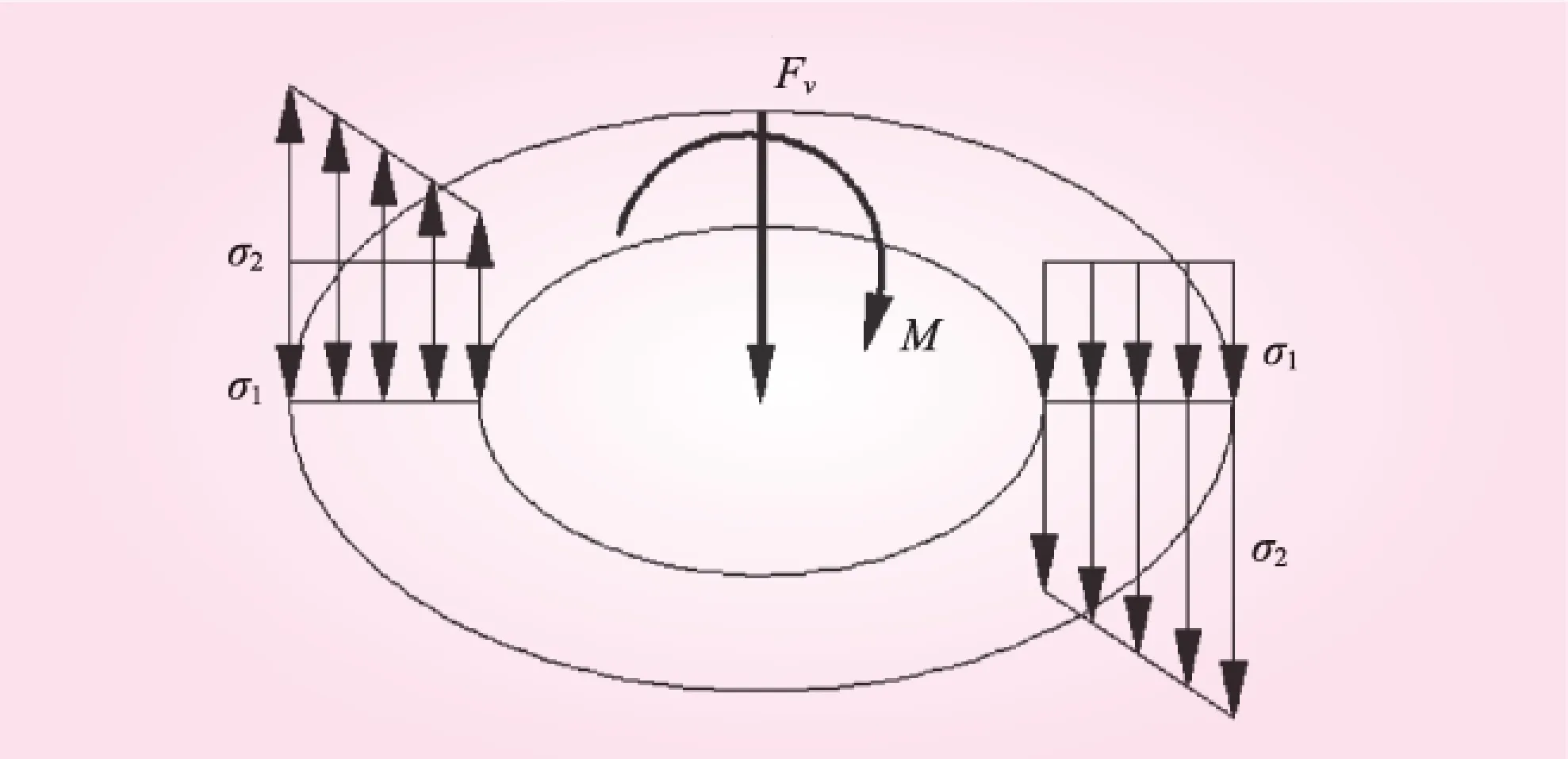
图2 1- 1剖面受力示意

从图1中可知，预应力锚杆一内一外两根为一组。假设为n组，将法兰面也分为n组，则可以求出这n组中法兰的最大压力F1和最大拉力F2。

(2)

对于法兰自身内部最大弯曲应力的计算，选取在法兰面n组中受压端受压力最大的一组隔离，法兰下端与灌浆层紧密接触，简化为弹性地基梁[8]计算，求出隔离体中最大弯矩Mmax，近似按照矩形截面求出抗弯截面系数Wz，从而得到法兰最大弯曲应力，如图3所示，图中Pa为锚杆的预紧力。

图3 法兰受压侧隔离段受力示意

1.2 灌浆层的最大压应力

因为灌浆层与混凝土承台之间不会出现法兰那样可能脱开的情况，因此灌浆层的受力主要考虑受压一侧的压应力是否在材料允许范围内。参考材料的自身属性，按照工程中常用的预紧力公式[9]可初步确定每一根锚杆的预紧力Pa，则灌浆层的最大压应力为

(3)

1.3 承台最大压应力

承台最大压应力与灌浆层的最大压应力在同一侧，受到灌浆层的直接压力，在不考虑上部力传递消散的情况下，承台最大压力Fct=Fgj，仅需要改变受力面积进行计算，即

(4)

式中，D3为灌浆层底面外径；D4为内径；Agj′为每组锚杆所在灌浆层在混凝土承台上的有效面积；σct为承台受压端的最大压应力。

1.4 锚固底板的最大弯曲应力

金属环锚固底板深埋在承台之中，是通过预应力锚杆与上部法兰连接，其主要受到预应力锚杆的拉力。按照以往的经验，在计算锚固底板时，选择相邻锚杆间的部分单独隔离，等效于两端固结梁或悬臂梁进行计算[5]，但实际上受拉端锚固底板下表面与混凝土部分有脱开的趋势，上表面则紧密接触。采用与法兰相同的计算方法，将隔离段等效为反向的弹性地基梁计算更为合理，隔离段材质为钢材，尺寸较小，刚度较大，按照混凝土相应的基床系数判别梁的类型为短梁，基底反力为均布力，可采用力学法进行计算[7]。

2 工程概况及应力计算

以一大型海上风电场风机基础为例进行计算。承台直径14 m，高5.6 m，材料为C50高性能混凝土，下部法兰外径为5.46 m，法兰宽0.48 m、厚0.08 m，法兰内径4.5 m。法兰内外两圈共布置200根锚杆，内圈锚杆中径4.76 m，外圈锚杆中径5.2 m，锚杆长4.1 m，锚杆的屈服强度为940 MPa。该连接方式为了避免法兰与承台直接接触导致承台表面受力过大，法兰与承台之间设置一层灌浆层，灌浆厚70 mm。下锚板尺寸为宽0.45 m、厚0.1 m。

根据式(1)～式(4)分别计算法兰的最大弯曲应力及灌浆层和承台的最大压应力，计算荷载和理论计算结果见表1。锚固底板隔离段，分别采用悬臂梁、固结梁以及连续梁方式进行计算，考察3种计算方式哪种更为合理。求出板中最大弯矩，按照平均截面面积求出抗弯截面系数，从而得到锚固底板最大弯曲应力。

表1 风电机组计算荷载及理论计算结果

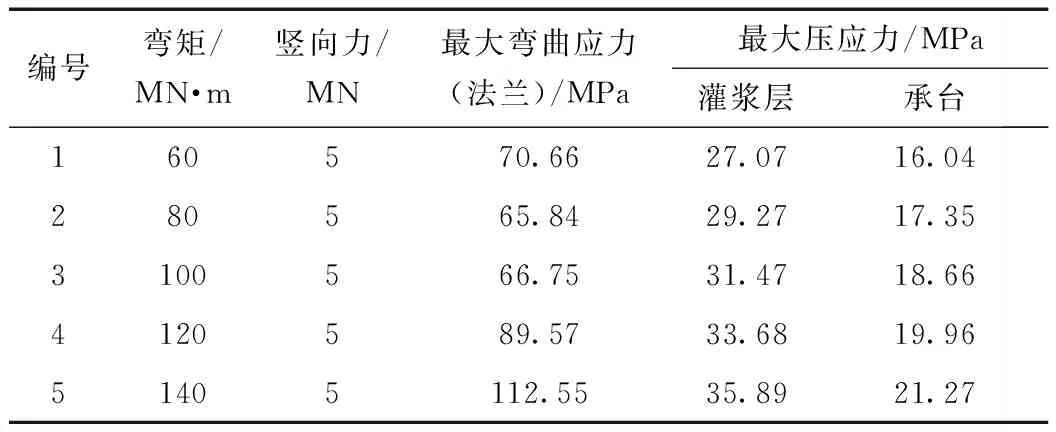
编号弯矩/MN·m竖向力/MN最大弯曲应力(法兰)/MPa最大压应力/MPa灌浆层承台160570.6627.0716.04280565.8429.2717.353100566.7531.4718.664120589.5733.6819.9651405112.5535.8921.27

当锚杆受力不超过预拉力时，传递到锚固底板的力主要由锚杆预拉力控制，受到风机荷载中弯矩变化影响非常小。在不同弯矩下，可认为锚固底板中弯曲应力不变。通过计算，悬臂梁、固结梁、连续梁的最大弯曲应力分别为1 043.0、215.51、72.18 MPa。

3 三维仿真模拟

3.1 有限元模型

为了验证计算公式的合理性，建立相应的三维有限元模型进行计算对比分析。采用大型有限元结构分析软件ABAQUS，锚杆笼模型如图4所示。基础过渡段、螺母、灌浆层、锚固板、混凝土承台采用八节点实体单元(C3D8R)离散，预应力锚杆采用桁架单元(T3D2)离散。锚杆两端通过锚固的方式分别固定在过渡段法兰和锚固板上，中间部分为无粘性连接段。螺母与法兰、灌浆层与承台之间通过软件中捆绑约束方式连接，法兰与灌浆层、锚固板与承台通过面-面接触连接，在锚杆作为桁架单元的条件下，锚杆两端采用嵌入方式与螺母和锚固板连接。

图4 锚杆笼模型

在传统的基础环模型中，法兰T形板的厚度及深度都会对基础环及混凝土承台的受力造成一定的影响[10- 12]，通过考察T形板的各种变量，来得到结构相对较合理的设计方案。为了研究锚杆笼结构中锚固板宽度对混凝土承台和锚杆的影响，模型采用5种锚固板的宽度，从0.45 m到0.65 m，每次间隔0.05 m，取固定弯矩60 MN·m，竖向力5 MN，进行多组模拟。

3.2 材料参数

钢材及混凝土的材料参数如表2所示。

表2 材料参数

材料弹性模量/GPa泊松比密度/kg·m-3钢筋和过渡段2100.37850承台混凝土C5034.50.22500灌浆层500.22400预应力锚杆2000.37850

混凝土材料考虑其非线形特性，C50轴心抗压强度标准值为32.4 MPa，轴心抗拉强度标准值2.64 MPa，其单轴压缩应力应变曲线见图5。灌浆层特征抗压强度为116 MPa。

图5 C50混凝土单轴压缩应力应变曲线

4 结果分析

按照表1的荷载分别计算不同弯矩下的各关键部位的应力状态。表3为不同弯矩荷载下法兰最大弯曲应力的理论值与有限元值，图6则为不同弯矩荷载条件下灌浆层和承台最大压应力变化曲线。

表3 有限元计算结果(法兰)

编号弯矩/MN·m最大弯曲应力/MPa16060.4828070.98310079.29412087.56514095.93

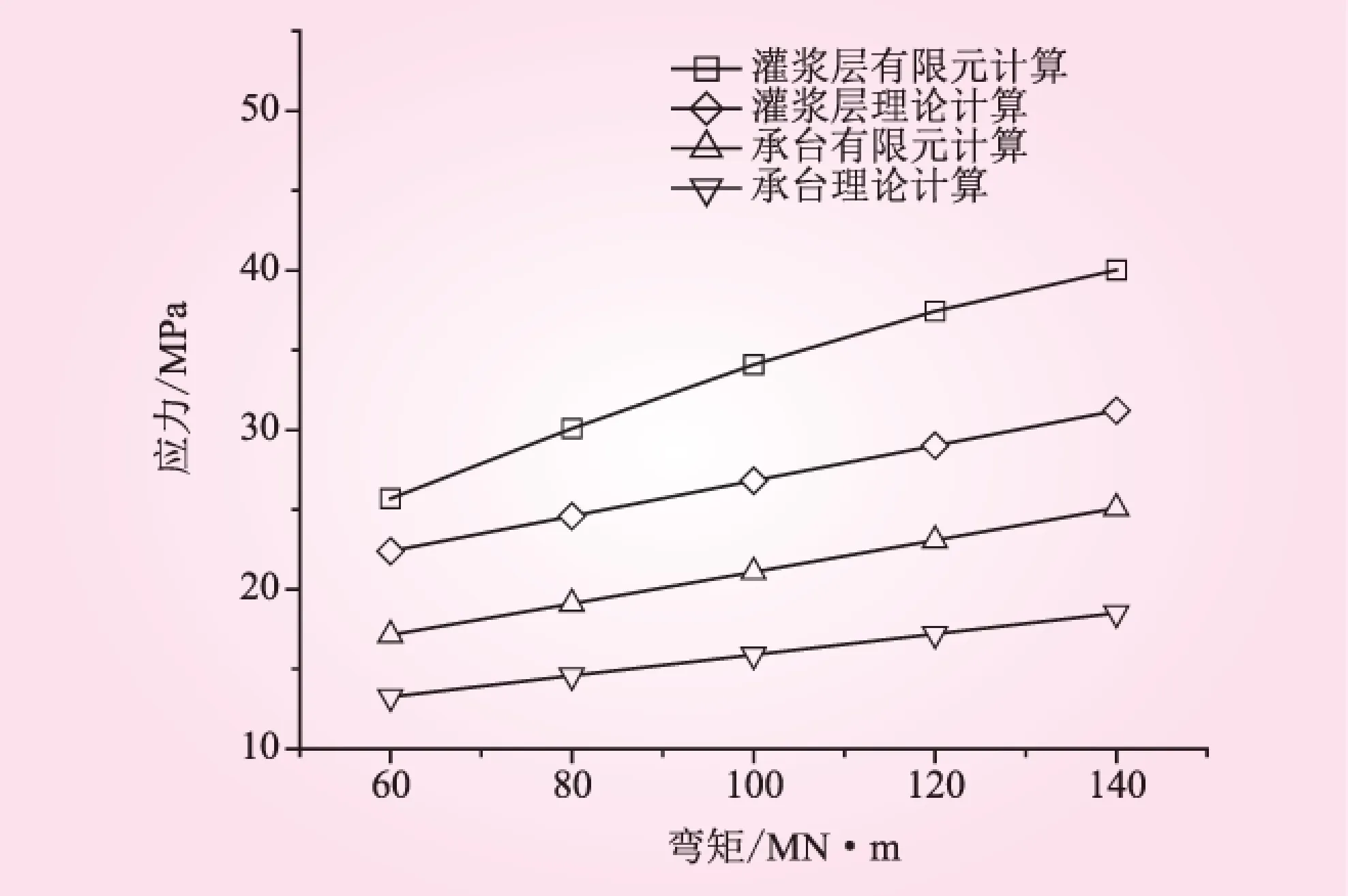
图6 灌浆层和承台受压端最大压应力

4.1 法兰受压端最大应力

从表1和表3中可知，法兰受压端最大弯曲应力理论计算值随着弯矩的增大先减小后增大，有限元计算值则一直增大。造成这个结果的原因是：理论计算中弯矩最大截面出现位置发生了变化，预应力锚杆附近和法兰中部都有可能出现最大弯曲应力。有限元计算中法兰的最大弯矩截面都出现在法兰中部。从数值上看，理论值稍偏大，最大相差为15%。

4.2 灌浆层和承台受压端最大应力

从图6中可知，灌浆层和承台最大应力都出现在受压端，其中有限元计算值大于理论计算值。当弯矩值为140MN·m时，两者的有限元值大于理论值的比例分别为28.2%和35.7%。造成这个结果有两个原因：①理论计算把具有柔性的承台和灌浆层当作刚体来进行计算，且计算出来的为受力面的平均应力，忽略了受力较大的情况下变形而导致的受力不均与应力集中现象。②在理论计算中，不同部件之间所有的连接方式都没有考虑相互之间的摩擦力，而在有限元计算中，法兰与灌浆层之间考虑了接触，存在摩擦力。

4.3 锚固底板的最大弯曲应力

不同弯矩下锚固底板有限元计算弯曲应力值见表4。由表4可知，锚固底板弯曲应力在弯矩增加的情况下几乎保持不变，说明上部的弯矩的变换对锚固底板影响非常小，这与理论计算中不考虑上部传导至锚固板的力而只考虑锚杆的预紧力是相符合的。在只考虑预紧力的情况下，相较于悬臂梁及固结梁，可以看出连续梁计算方式更接近于有限元数值，理论值大于有限元值30%左右。

表4 不同弯矩下的锚固底板弯曲应力

编号弯矩/MN·m弯曲应力/MPa16050.9228051.21310051.53412051.86514052.18

4.4 锚固底板尺寸影响

当其他结构保持一致，仅锚固板尺寸发生改变时，整个结构受力基本相同。分别取锚固板尺寸为45～65 cm，每次增加5 cm，分为5组进行计算。主要考察锚固板应力、锚固底板与承台的接触应力等。结果表明，不同锚固板的宽度时，锚固板的应力最大变幅在2 MPa左右，变化较小；接触应力在16.6 MPa，变化较小。

5 结 语

在实际工程的基础上，通过理论推导和有限元相互验证的方法，对海上风电预应力锚杆笼基础开展研究，主要结论为：①提出的理论计算方法能够较准确地计算法兰、灌浆层及承台的应力。②采用弹性地基梁计算方法分析锚固底板应力更接近实际应力状态。③对于结构局部关键应力分析，建议采用三维有限元方法进行复核，确保结构安全。

[1]WANG Wei， BAI Yong. Investigation on Installation of Offshore Wind Turbines[J]. Journal of Marine Science and Application， 2010， 9(2)： 175- 180．

[2]刘润， 陈广思， 刘禹臣， 等. 海上风电大直径宽浅式筒型基础抗弯特性分析[J]. 天津大学学报： 自然科学与工程技术版， 2013， 46(5)： 393- 400．

[3]张万祥， 刘洪海， 于春来. 新型风力发电机组梁板式预应力锚栓基础应用[J]. 风能， 2014(5)： 84- 86．

[4]傅式尹. 套管—锚板式地脚螺栓[J]. 重型机械， 1995(1)： 64- 65．

[5]郭敏， 谢超， 谢治， 等. 预应力风电机组基础锚杆笼连接计算方法研究[J]. 风能， 2014(5)： 79- 82.

[6]刘胜祥， 宋晓萍， 向继超. 大型风机连接螺栓的疲劳特性分析[J]. 水电能源科学， 2013， 31(7) ： 170- 172．

[7]王世斌， 亢一澜. 材料力学[M]. 北京： 高等教育出版社， 2008．

[8]吴兴序. 基础工程[M]. 成都： 西南交通大学出版社， 2007．

[9]成大先. 机械设计手册[M]. 北京： 化学工业出版社， 2004．

[10]李振作. 中欧预应力重力式风机基础设计方法分析与比较[J]. 山西建筑， 2014， 40(7)： 69- 71．

[11]张立英. 风机基础结构数值模拟及优化设计研究[D]. 天津： 天津大学， 2004．

[12]练继建， 刘喜珠， 张立英， 等. 风机基础钢混组合结构细部损伤分析研究[J]. 水利水电技术， 2011， 42(1)： 48- 53．

(责任编辑 王 琪)

Research on Structural Design Method of Foundation with Pre-stressed Anchor Cage for Offshore Wind Turbine Generator

WANG Haijun, JIANG Xingyu

(School of Civil Engineering, Tianjin University, Tianjin 300072, China)

The foundation with pre-stressed anchor cage for offshore wind turbine generators is a new-style foundation. The theoretical calculation methods of connect flange, grouting layer, platform and anchor plate of this foundation are proposed by the means of mechanical method. In order to verify these methods, the finite element simulation is carried out. The results show that： (a) the new methods can accurately calculate the stresses of connect flange, grouting layer and concrete platform; and (b) for anchor plate stress analysis, the elastic foundation beam method is more reasonable than consolidation beam and cantilever beam methods which are proposed based on existing experiences. The effects of anchor plate sizes on the stresses of flange, grouting layer and anchor plate are also studied, and according to the results, the anchor plate sizes are optimized to provide reference to actual engineering．

offshore wind power; foundation with pre-stressed anchor cage; design method; stimulation; anchor plate

2015- 11- 09

国家创新研究群体科学基金(51321065)；高等学校学科创新引智计划资助(B14012)；国家自然科学基金(51508558)

王海军(1978—)，男，江西萍乡人，副教授，博士，主要从事水工结构静动力特性方面的研究．

TM614；P752

A

0559- 9342(2016)06- 0084- 04