水工隧道动力深、浅埋划分限界研究及试验验证
2016-11-22吕晓春
张 碧,吕晓春
(1.陕西铁路工程职业技术学院,陕西渭南714000;2.华北水利水电大学资源与环境学院,河南郑州450011)
水工隧道动力深、浅埋划分限界研究及试验验证
张 碧1,吕晓春2
(1.陕西铁路工程职业技术学院,陕西渭南714000;2.华北水利水电大学资源与环境学院,河南郑州450011)
隧道动力深、浅埋划分限界属于隧道结构的固有特性,受围岩类别、隧道结构形状、隧道跨度等因素的影响,不受外界因素(如地震波种类等)的影响。计算分析和振动台模型试验验证表明,隧道动力深、浅埋划分限界值受围岩类别的影响较大;矩形隧道对其敏感性较大,圆形隧道的敏感性较小;隧道跨度对其有一定的影响。
隧道;动力划分限界;振动台试验;地震波
0 引 言
截至目前,全球发生过许多次重大地震。在这些地震中,隧道结构都发生了不同程度的破坏。震害统计发现,隧道埋深大于50 m 时破坏程度明显减小,在300 m以下没有严重的破坏,受破坏的地下洞室有35%的埋深小于50 m[1]。在地震作用下,隧道埋深对隧道的受力和变形有很大影响,对深、浅埋隧道需要采用不同的计算方法。目前,公路隧道抗震设计中或者没有区分深、浅埋,或者仍然采用静力分析中深、浅埋划分方法[2],不能反应出地震波作用的动力实质。因此,进行隧道动力深、浅埋划分限界研究是必要的。
隧道埋深是影响地震动力响应的一个重要因素。舒亚俐等[3]对不同埋深构筑物的动力响应进行研究认为,构筑物的振动频率随埋深的增加而增大,总体位移随埋深的增加而减少,地震惯性力随埋深增加而减小;郑永来等[4]对国内外城市地下结构的震害情况进行统计分析后认为,地下管道的破坏随埋深的增加而减小,地下结构埋深越大,由地震面波导致的能量越小,震害应减轻;于翔[5- 6]分析了1995年阪神地震中地下结构的破坏情况发现,上层破坏比下层破坏严重,地下结构上部土层越厚,破坏越轻;李海波等[7]研究了地震荷载作用下地下岩体洞室位移特征的影响因素认为,地下洞室位移响应随埋深的增加而减小,洞室位移响应存在临界埋深;李加林等[8]运用FLAC就珠三角软土地层隧道埋深对地铁运行诱发的相关振动影响规律进行分析表明,埋深越浅则动力响应越强,埋深越大则动力响应越弱;郑颖人等[9]通过模型试验与数值分析方法研究了静力条件下隧道从浅埋到深埋的破坏过程,根据压力拱(普氏压力拱) 确定深、浅埋的分界线。
以上研究表明,隧道埋深对隧道地震响应有很大的影响,但依靠静力条件下的划分标准确定地震作用下隧道的动力深、浅埋是不准确的,有关隧道动力深、浅埋划分方面的研究还未见相关报道。为此,本文通过数值计算和振动台模型试验,划分隧道动力深、浅埋。
1 数值计算原理与方法
计算中将隧道作为平面应变问题处理,隧道衬砌和围岩均采用块体(Plane42 单元,二维实体结构模型用作平面应变单元),围岩的破坏准则采用D-P准则,计算模型的尺寸高h×宽b=300 m×500 m,模型左、右两侧使用粘弹性边界,使用弹簧单元combin14模拟。计算模型见图1。具体的弹性和阻尼参数计算如下
(1)
CBT=ρcS
CBN=ρcP
式中,KBT、KBN分别为切向和法向弹簧的弹性系数;CBT、CBN分别为切向和法向的阻尼系数;ρ为围岩的密度;R为边界点到隧道中心的距离;cS、cP分别为地震横波波和纵波波速;kT、kN为调整系数,在0.5~1.2的范围内取值,通过数值试算确定[10]。
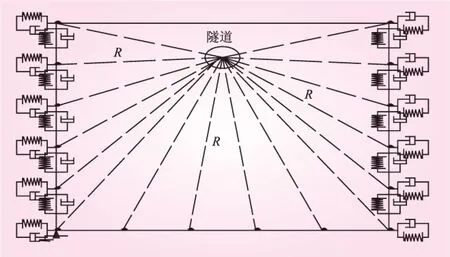
图1 计算模型
为了对比分析,隧道采用矩形、马蹄形和圆形隧道结构。动力阻尼C采用瑞利阻尼,即
C=αM+βK
(2)
式中,M为系统质量矩阵;K为刚度矩阵;α为与质量成比例的阻尼系数;β为与刚度成比例的阻尼系数。
对于多自由度系统,任意系统角频率ωi的临界阻尼比ξi是角频率为ωi的第i阶模态临界阻尼的一部分,可以从下式得到
(3)
模拟计算隧道结构在El_Centro地震波(前8.0s)和2008年汶川地震波作用下的地震响应,两者的频率和峰值分布不同,对比分析可以反应出隧道结构的波动特性。加速度峰值均取0.3g。相关输入地震波时程见图2。
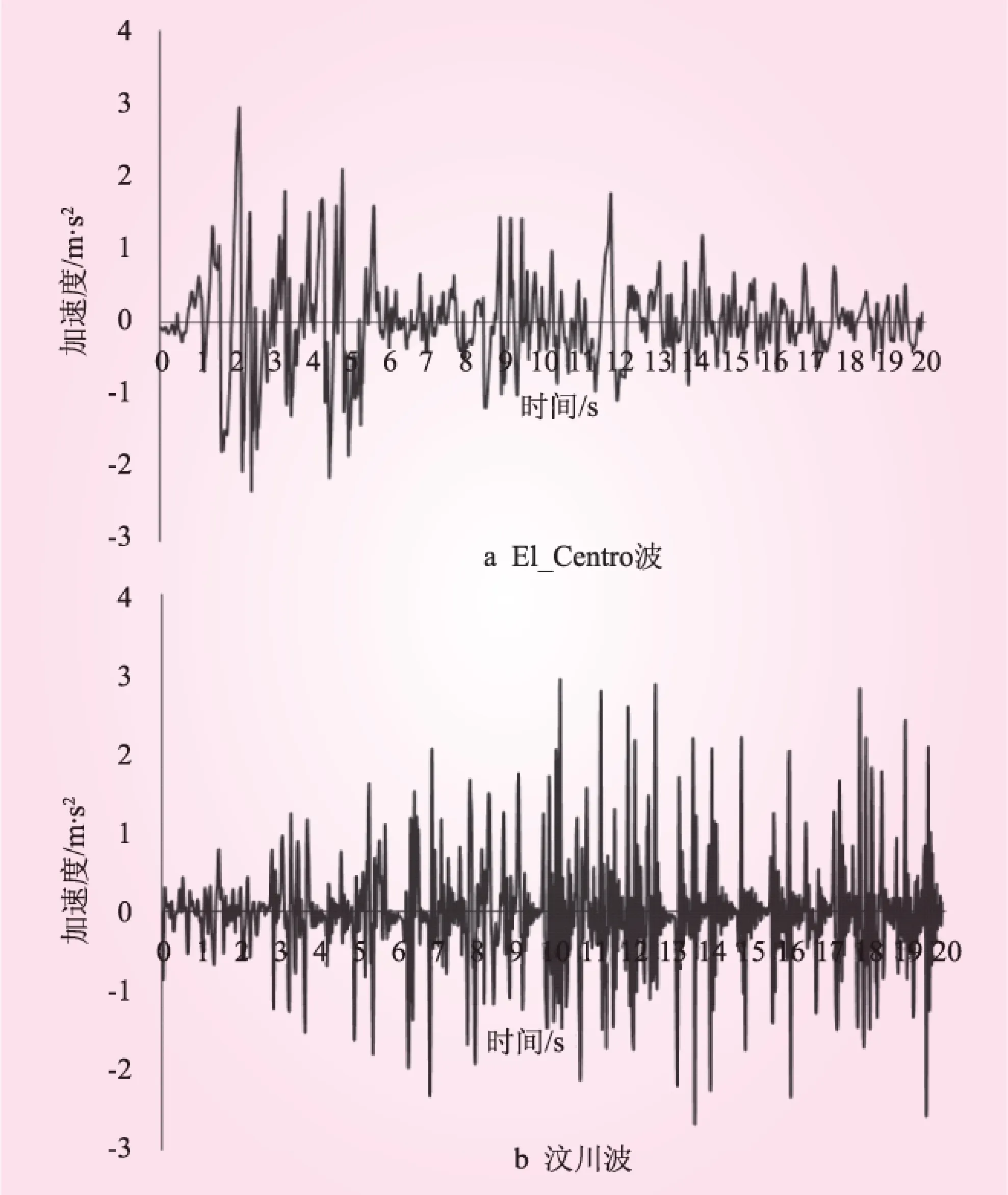
图2 输入地震波时程
2 数值计算结果分析
2.1 不同围岩类别
本节计算时,选取隧道结构为马蹄形,输入El_Centro地震波,提取了衬砌外侧拱顶处的剪切应力τxy。不同围岩类别衬砌应力随隧道埋深变化见图3。图中,B为隧道跨度。
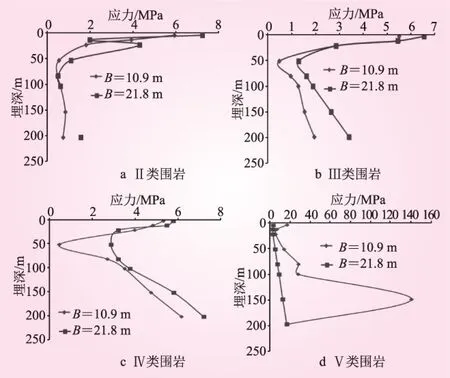
图3 不同围岩类别衬砌应力随隧道埋深变化
从图3可知,在地震波作用下,隧道衬砌的剪应力在随埋深变化中存在拐点,拐点处的隧道埋深可作为隧道动力深、浅埋限界;隧道动力深、浅埋限界受围岩类别影响较大;隧道跨度对隧道动力深、浅埋限界有一定的影响(图3d中,埋深150 m处数值有突变,应是计算误差所致,可忽略)。
2.2 不同隧道结构形状和跨度对比
为了分析影响隧道动力深、浅埋限界的影响因素,本节考虑了隧道结构形状和隧道跨度2种因素进行了对比分析。不同隧道结构形状衬砌应力随隧道埋深变化见图4。
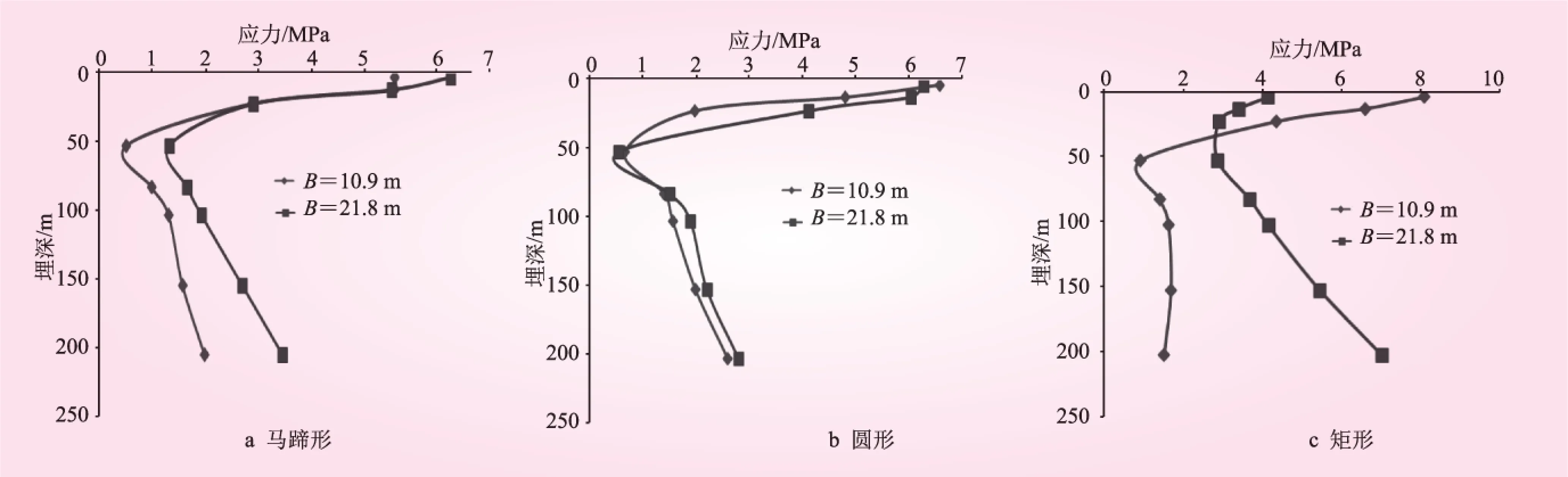
图4 衬砌应力随隧道埋深变化
由图4可知,隧道结构形状对隧道动力深、浅埋限界的影响不大;在不同的隧道结构形状条件下,隧道跨度对隧道衬砌动应力和隧道动力深、浅埋限界的敏感性不同。其中,圆形隧道的敏感性较小,矩形隧道的敏感性最大;隧道跨度对隧道动力深、浅埋限界有一定的影响,但对不同结构形状隧道的影响不同,对矩形隧道影响最大,对圆形隧道影响最小。
2.3 不同地震波对比
由上述分析可知,矩形隧道衬砌动应力对隧道动力深、浅埋限界的敏感性最强。本节计算分析了矩形隧道在El_Centro波和汶川波2种不同地震波(同为0.3g)作用下隧道动力深、浅埋限界的变化(见图5)。
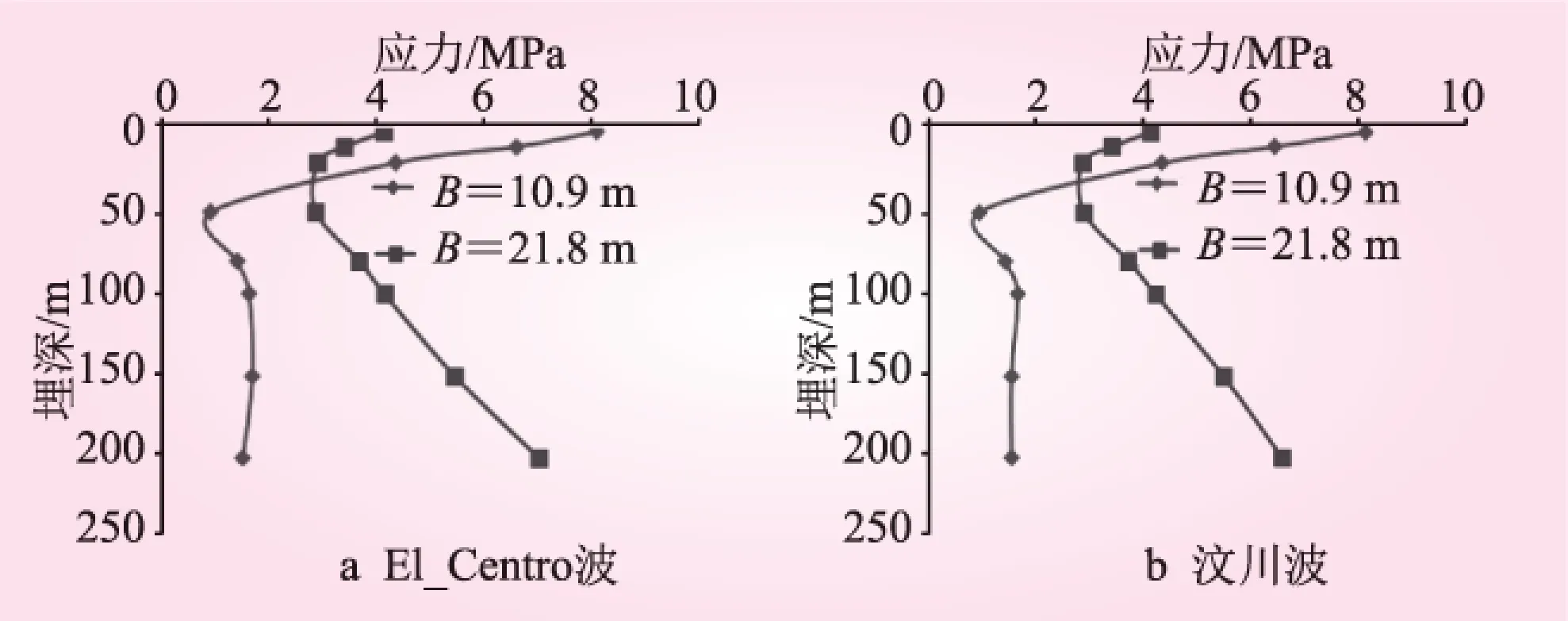
图5 不同地震波作用下衬砌应力随隧道埋深变化
从图5可知,地震波种类的不同对隧道动力深、浅埋限界的影响不明显;隧道动力深、浅埋限界应该是隧道自身的特性,与所受的地震波种类关系不大。
3 振动台模型试验设计
本试验是为了验证地震作用下隧道结构的响应规律,属于动力试验,应该用到动力相似准则。动力学运动方程可用矩阵方程表示如下
[M][a]+[C][v]+[K][u]=[F]
(4)
式中,[M]为质量矩阵;[a]为加速度矩阵;[C]为阻尼矩阵;[v]为速度矩阵;[K]为刚度矩阵;[u]为位移矩阵;[F]为荷载矩阵。
本试验为对比验证性试验,综合考虑振动台承载能力、台面尺寸、具体隧道尺寸和制作工艺等多种因素,对隧道原型进行适当简化,试验用长50 cm、宽50 cm、高80 cm的模型箱作为隧道洞口段模型,几何相似比为1∶40;隧道衬砌采用了圆形衬砌,外径15 cm,衬砌厚度1 cm。试验模型见图6。图中虚线所示的衬砌为在不同深度处埋设衬砌,以模拟不同隧道埋深情况。
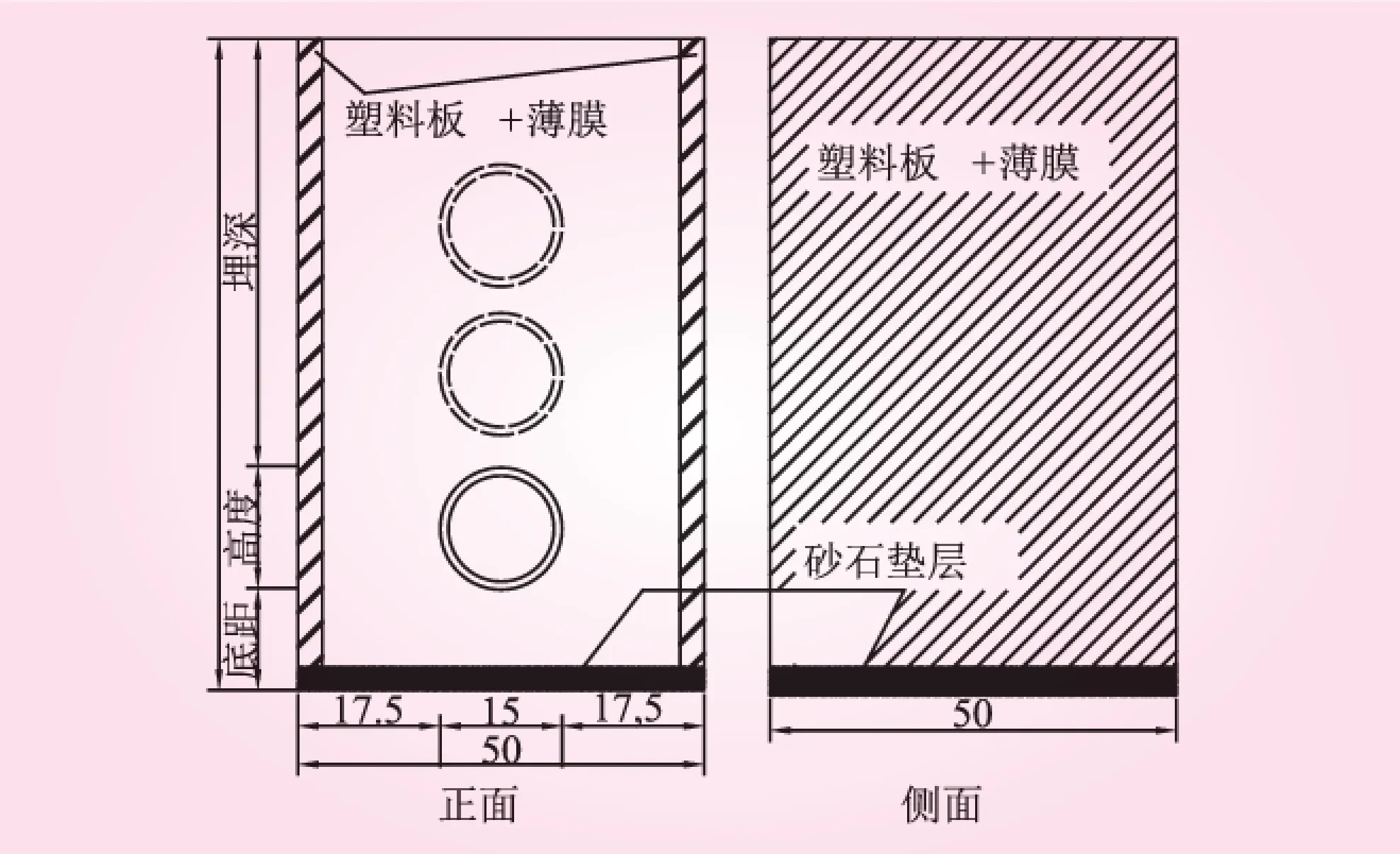
图6 振动台试验模型(单位:cm)
振动台提供水平方向的地震波输入,输入的地震波为El_Centro地震波(前8.0 s)和2008年汶川地震波,地震波的加速度峰值均取0.1g、0.2g、0.3g和0.4g。
用高强石膏模拟衬砌,用粉煤灰、石英砂、石膏、锯末和机油的混合物模拟围岩。石膏和机油主要等效围岩的粘聚力c值[11],粉煤灰和石英砂作为主要的骨料,通过调节其密度使颗粒级配满足试验要求。在确定衬砌材料时,根据水膏比为0.8∶1、0.9∶1、1∶1、1.1∶1和1.2∶1等5种情况分别做成标准圆柱体试件,然后放在万能试验机上进行分级加载压缩试验,确定其弹性模量在0.5~2.9 GPa。实际隧道一般采用C25混凝土作为二衬材料,其弹性模量为17.5~30 GPa。确定衬砌材料的弹性模量相似比为1∶20,据此选用水膏比为1.05∶1。将粉煤灰、石英砂、石膏、锯末和机油等材料按照不同的配合比进行混合[12],参照实际围岩材料的物理性质指标,进行正交试验来确定试验材料的相似比。
将隧道衬砌外侧上(Y1)、下(Y2)、左(Y3)和右(Y4)4个部位(见图7)的剪切应力测试结果统计绘图(见图8)。振动台试验结果与前述的数值计算结果对比分析可知,隧道振动台模型试验进一步验证了隧道动力深、浅埋限界的存在;振动台模型试验的结果与数值计算结果基本一致(限界值均在45~50 m);隧道衬砌不同部位(上、下、左、右)处的动力深、浅埋限界值基本一致。
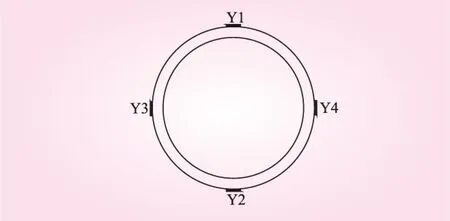
图7 测试点布置
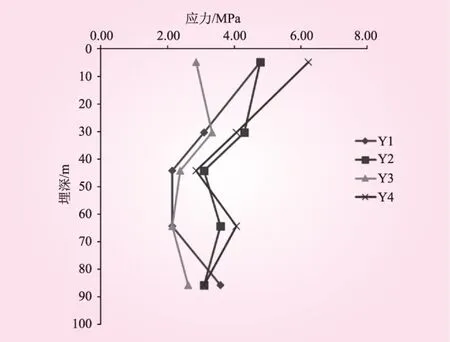
图8 振动台试验结果
4 结 语
通过计算分析和振动台模型试验,证明了隧道动力深、浅埋限界的存在,并分析了其影响因素。得到如下结论:
(1)计算分析发现隧道动力深、浅埋限界是确实存在的,且与隧道的静力深、浅埋限界值有所区别。
(2)隧道动力深、浅埋限界与围岩类别、隧道结构形状、隧道跨度等因素有关,属于隧道结构的内在特性,与所受地震波的种类无关。
(3)隧道动力深、浅埋限界值受围岩类别的影响较大;隧道结构形状影响因素中,圆形隧道的敏感性较小,矩形隧道的敏感性最大;隧道跨度对动力深、浅埋限界值有一定的影响。
(4)隧道振动台模型试验验证了隧道动力深、浅埋限界的存在,并且得到了与数值计算一致的结论。
[1]SHARMA S, JUDD W R. 地震对地下洞室的破坏[J]. 雷谦荣, 译. 地下空间, 1992, 12(4): 335- 344.
[2]JTG/T D70—2010 公路隧道设计细则[S].
[3]舒亚俐. 构筑物不同埋深时地震动反分析探讨[J]. 特种结构, 1997, 14(4): 49- 55.
[4]郑永来, 杨林德. 地下结构震害与抗震对策[J]. 岩石力学与工程学报. 2001, 20(1): 70- 73.
[5]于翔. 地铁建设中应充分考虑抗地震作用—阪神地震破坏的启示[J]. 铁道建筑技术, 2000(6): 32- 35.
[6]于翔. 地下建筑结构应充分考虑抗震问题—1995年阪神地震破坏的启示[J]. 工程抗震, 2002(4): 17- 20.
[7]李海波, 马行东, 李俊如, 等. 地震荷载作用下地下岩体洞室位移特征的影响因素分析[J]. 岩土工程学报, 2006, 28(3): 358- 362.
[8]李加林, 邓飞皇. 隧道埋深对地铁运行诱发振动的影响分析[J]. 科学技术与工程, 2007, 7(15): 3819- 3822.[9]郑颖人, 徐浩, 王成, 等. 隧洞破坏机理及深、浅埋分界标准[J]. 浙江大学学报: 工学版, 2010, 44(10): 1851- 1856.
[10]杜修力, 赵密, 王进廷. 近场波动模拟的人工应力边界条件[J]. 力学学报, 2006, 38(1): 49- 56.
[11]王明年, 林国进, 于丽, 等. 隧道抗震与减震[M]. 北京: 科学出版社, 2012.
[12]蒋树屏, 蒋华, 王晓雯, 等. 高烈度地震区公路隧道洞口段大型振动台模型试验方案设计[J]. 公路, 2009(10): 245- 249.
(责任编辑 杨 健)
Study on the Dynamic Bound of Shallow Buried and Deep Buried Hydraulic Tunnel and Its Experimental Verification
ZHANG Bi1, LÜ Xiaochun2
(1. Shaanxi Railway Institute, Weinan 714000, Shaanxi, China; 2. School of Resources & Environment,North China University of Water Resources and Electric Power, Zhengzhou 450011, Henan, China)
The dynamic bound of shallow buried and deep buried hydraulic tunnel is the intrinsic characteristics of tunnel structure, which is affected by surrounding rock types, tunnel structure shapes, tunnel span and others, and not affected by external factors (such as the type of seismic wave). The calculation and shaking table test show that, the dynamic bound values of shallow buried and deep buried tunnel are strongly influenced by rock type, the rectangular tunnel has big sensitivity and in contrary the circular tunnel has small one, and the tunnel span has a certain influence on dynamic bound values.
tunnel; dynamic bound; shaking table test; seismic wave
2016- 03- 03
国家自然科学基金资助项目(81408222)
张碧(1979—),男,山西沁县人,副教授,硕士,主要从事道路与铁道工程专业的教学和研究工作.
TV312
A
0559- 9342(2016)06- 0026- 04
