具有连续时滞的反馈控制合作系统的持久性

张恩培, 李 星, 吴呈良, 董 魁

(中国地质大学(武汉) 数理学院, 湖北 武汉 430074)



具有连续时滞的反馈控制合作系统的持久性

张恩培, 李 星, 吴呈良, 董 魁

(中国地质大学(武汉) 数理学院, 湖北 武汉 430074)

研究了一类具有连续时滞的反馈控制合作系统.通过利用一种不等式分析方法, 建立了保证系统持久性的充分条件,结果表明反馈控制变量对系统的持久性没有影响.

连续时滞; 反馈控制; 持久性; 合作系统

种群的持久存在性历来是人们关注的焦点.通过在种群模型中引入反馈控制项,可以对生物种群进行调整,维持生物种群的数量稳定性.目前,关于反馈控制合作系统的动力学行为研究已经很多了[1-7].如Chen对一类具连续时滞的反馈控制May合作种群的持久性进行了分析[2];He则讨论了离散时滞的情形[4].本文考虑了如下具有连续时滞和反馈控制的n种群合作系统,

(1)

式中,Ni(t)(i=1,…,n)代表第i个合作种群的密度,ui(t)(i=1,…,n)代表反馈控制变量,系统有如下假设:

(H1)ri(t),Ki(t),αij(t),di(t),ai(t),bi(t),i,j=1,2,…,n.是连续的实值函数,且上下界均为正常数,αij(t)>Ki(t),i,j=1,2,…,n,j≠i.

(H2)Tij,σi,δi,ηi是正常数,Pij(s),Gi(s),Hi(s),Li(s)是非负连续函数且满足

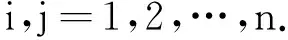
(2)

令τ=max{Tij,δi,σi,ηi,i,j=1,2,…,n.},初始条件为

(3)

由泛函微分方程定理[8]不难看出,当t≥0时,解满足

对于一个定义在R上的有界连续函数g,有如下的定义:

gl=infg(t),gu=supg(t).

1 预备知识

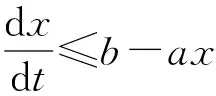
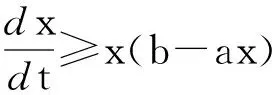
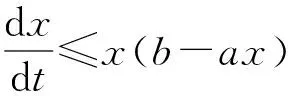
引理5[10]假设a>0,b(t)>0是有界连续函数,x(0)>0,进一步假定

对所有的t≥θ≥0,

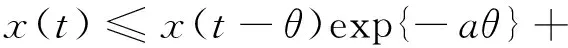
特别地,如果b(t)的上界对应的是M,那么

引理6[10]假设a>0,b(t)>0 是有界连续函数,x(0)>0,进一步假定

对所有的t≥θ≥0,

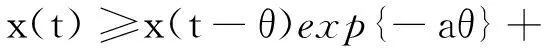
特别地,如果b(t)的上界对应的是m,那么

定理1 假设(H1)和(H2)均成立,则满足初始条件(2)的系统(1)是持久的,即存在两个独立于系统(1)的解的正常数m和M,对于系统(1)的任意正解,有

2 系统的上界分析

引理7 假设(N(t),u(t))=(N1(t),…,Nn(t),u1(t),…,un(t))是系统(1)的任意正解,则存在一个独立于系统(1)解的正数M,使得

证明 假设(N(t),u(t))=(N1(t),…,Nn(t),u1(t),…,un(t))是系统(1)满足初始条件(2)的解.根据系统(1)第i个方程可知,当t≥0时,

(4)

(5)

将式(5)代入系统(1)的第i个方程得

(6)

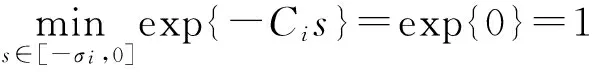
由引理4得:

(7)

因此,存在T1>0,当t>T1时,得Ni(t)≤2M1i,由系统(1)的第n+i式可知

(8)

式(8)由引理2得:

(9)

让M=max{M1i,M2i},i=1,2…,n很显然,M独立于系统的解,引理得证.

3 系统的下界分析

引理8 假设(N(t),u(t))=(N1(t),…,Nn(t),u1(t),…,un(t)) 是系统(1)的任意正解,则存在一个独立于系统(1)解的正数m,使得

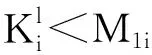
(10)

根据系统(1)的第i个方程可知,当t≥T2+τ,

(11)

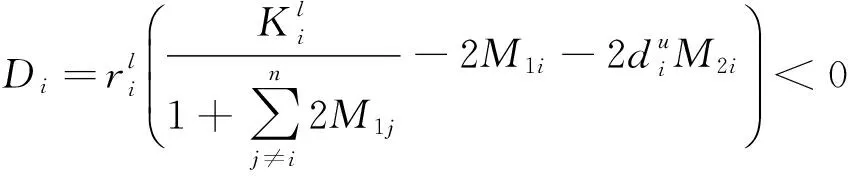
因此,

(12)

将式(12)代入到系统(1)第n+i个方程得:

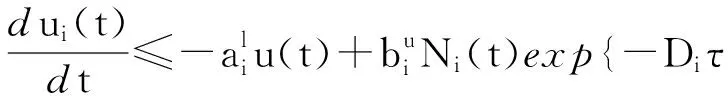
(13)

运用引理5可得,当t≥θ≥T2+τ时,

(14)

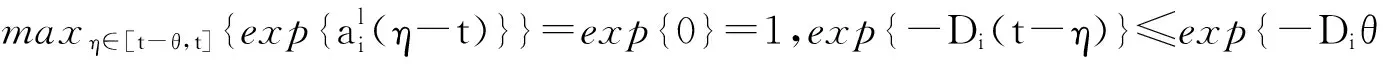
假设存在一个γi>0,使得当|s|≥γi时,

(15)

因此,

(16)

可以选取任意满足上面条件的正常数γi.选定γi,对于所有的t≥T2+τ+γi,得

(17)

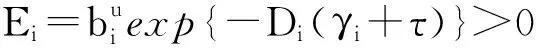
(18)

因此,

(19)

其中maxs∈[-δi,0]exp{-Dis}=exp{0}=1.

将式(19)代入系统(1)第i个式子,当t≥T2+τ+γi时,得

(20)

由引理3可得

(21)

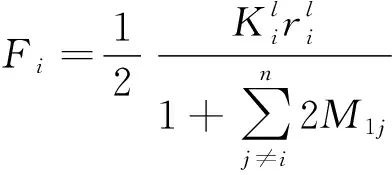
存在一个T3>max{T2+τ+γi},i=1,2,…,n.当t≥T3时,

(22)

将式(22)代入系统(1)的第n+i个方程得

(23)

因此,由引理1可得

(24)

令m=min{m1i,m2i},m独立于系统的解,因此引理8得证.

4 结 论

由引理7和8证明可知,定理1的结论是显然的.针对系统(1)持久性问题,在初始条件下,首先利用不等式放缩方法,讨论了系统(1)的上界有界存在性问题.在此基础上,对系统(1)的下界采用不等式分析方法进行研究,证明了系统(1)下界是有界的,进而建立了系统持久性的充分条件,结果表明了反馈控制变量对系统(1)的持久性没有影响.

[ 1 ]CHENFD,YANGJH,CHENLJ,etal.Onamutualismmodelwithfeedbackcontrols[J].AppliedMathematicsandComputation, 2009,214(2):581-587.

[ 2 ]CHENLJ,XIEXD.PermanenceofanNspeciescooperationsystemwithcontinuoustimedelaysandfeedbackcontrols[J].NonlinearAnalysis:RealWorldApplications, 2011,12(12):34-38.

[ 3 ]CHENFD,LIAOXY,HUANGZK.ThedynamicbehaviorofN-speciescooperationsystemwithcontinuoustimedelayandfeedbackcontrols[J].AppliedMathematicsandComputation, 2006,181(2):803-815.

[ 4 ]HEWL.PermanenceandglobalattractivityofN-speciescooperationsystemwithdiscretetimedelaysandfeedbackcontrols[J].AnnalsofDifferentialEquations, 2007,23(1):3-10.

[ 5 ] 白萍,王治民.具生物控制的非自治多种群互惠系统的全局吸引性[J]. 吉林大学学报(理学版), 2012,50(4):633-637.

(BAIP,WANGZM.Globalattractivityofnonautonomousmultiplespeciescooperativesystemwithbiocontrols[J].JournalofJilinUniversity(ScienceEdition), 2012,50(4):633-637.)

[ 6 ]LIYK,ZHANGTW.Permanenceofadiscreten-speciescooperationsystemwithtime-varyingdelaysandfeedbackcontrols[J].MathematicalandComputerModelling, 2011,53(5/6):1320-1330.

[ 7 ]YANGWS,LIXP.PermanenceofadiscretenonlinearN-speciescooperationsystemwithtimedelaysandfeedbackcontrols[J].AppliedMathematicsandComputation, 2011,218(7):3581-3586.

[ 8 ]HALEJK.Theoryoffunctionaldifferentialequations[M].Heidelberg:Springer-Verlag, 1997.

[ 9 ]CHENFD,LIZ,HUANGYL.Noteonthepermanenceofacompetitivesystemwithinfinitedelayandfeedbackcontrols[J].NonlinearAnalysis:RealWorldApplications, 2007,8(2):680-687.

[10]CHENFD,YANGJH,CHENLJ.Noteonthepersistentpropertyofafeedbackcontrolsystemwithdelays[J].NonlinearAnalysis:RealWorldApplications, 2010,11(2):1061-1066.

【责任编辑: 肖景魁】

Permanence of a Cooperative System with Continuous Time Delays and Feedback Controls

Zhang Enpei, Li Xing, Wu Chengliang, Dong Kui

(SchoolofMathematicsandPhysics,ChinaUniversityofGeosciences,Wuhan430074,China)

Acooperativesystemwithcontinuoustimedelaysandfeedbackcontrolsisstudied.Byapplyinganinequalityanalysismethod,thesufficientconditionswhichensurethepermanenceofthesystemareestablished.Theresultshowsthatthefeedbackcontrolvariableshavenoinfluenceonthepersistentpropertyofthesystem.

continuoustimedelays;feedbackcontrol;permanence;cooperativesystem

2016-05-10

国家重点基础研究发展计划资助项目(2012CB955700).

张恩培(1990-),男,河北三河人,中国地质大学(武汉)硕士研究生; 李 星(1962-),男,天津人,中国地质大学(武汉)教授.

2095-5456(2016)05-0425-04

O 175.14

A