可变模态分解算法及其在天然气管道泄漏检测中的应用

路敬祎 马雯萍 高丙坤 刘 伟 高 薇

(东北石油大学电气信息工程学院,黑龙江 大庆 163318)

可变模态分解算法及其在天然气管道泄漏检测中的应用

路敬祎 马雯萍 高丙坤 刘 伟 高 薇

(东北石油大学电气信息工程学院,黑龙江 大庆 163318)

对可变模态分解算法在天然气管道泄漏信号检测中的应用做了研究。通过对其噪声鲁棒性、过度分解和不饱和分解特性的分析，并与经验模态分解和小波分解进行对比，证明可变模态分解算法在天然气管道泄漏信号检测与分析方面的可行性和有效性，并且可变模态分解具有更好的噪声鲁棒性和泄漏信号检测效果。

管道泄漏 可变模态分解 经验模态分解 小波分解 Matlab

近年来，随着天然气管道运行年限的增加和人为破坏，管道盗气行为逐渐增多、泄漏风险逐年加大，管道一旦发生泄漏，将影响输气系统的正常运行，造成严重的环境污染和经济损失。目前，天然气管道泄漏检测方法有很多，主要有应用统计法、红外热成像法、分布式光纤法及声波法等。其中声波法因其原理简单、维护费用低而得到了应用广泛。文献[1]将声波法与经验模态分解(Empirical Mode Decomposition,EMD)结合，并对该新方法在天然气管道泄漏信号检测中的应用做了详细研究。文献[2]在理论上详细介绍了EMD信号的分析方法。

2013年，Dragomiretskiy K和Zosso D提出了可变模态分解(Variational Mode Decomposition,VMD)[3]，其实质是经典维纳滤波在多个自适应波段的推广，通过迭代搜寻变分模式的最优解获得中心频率与带宽限制，在频域上自适应地分解出各中心频率对应的有效成分，以得到模态函数；通过对管道检测信号做VMD分解提取出所需低频段的模态函数，以进行时域和频域分析，与小波分解对比可知，VMD在特征提取方面具有更好的准确性和稳定性。在此，笔者基于VMD算法对天然气管道泄漏产生的噪声进行检测分析，并将结果与小波分解和EMD算法进行对比。

1 VMD算法①

VMD算法首先假设每个模态函数uk是围绕中心频率的有限带宽[4]，通过变分模型确定并实时估计相应的频段和模态函数。估计每个模型uk的带宽的步骤如下：

a． 通过Hilbert变换[5,6]，计算每个uk的解析函数以获得相应的边际谱；

b． 通过指数混合调制到估算的中心频率，将每个模型uk的频谱转移到基带[7]；

c． 由解调信号的高斯光滑度和梯度平方准则来估计带宽。

由上述步骤得到的约束变分问题为：

其中，uk={u1,u2,…,uk}为各模态函数，wk={w1,w2,…,wk}为各中心频率。

通过引入拉格朗日乘子λ(t)和二次惩罚因子α将约束变分问题转变为非约束变分问题，二次惩罚因子是典型的实现重构信号保真度的方法，拉格朗日乘子则用来实现精确重构。将两者结合得到拓展的拉格朗日表达式如下：

L({uk},{wk},λ):

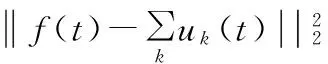
采用乘法算子交替方向法解决上述变分问题，迭代优化uk+1、wk+1、λk+1即可求得扩展拉格朗日表达式的“鞍点”。

2 VMD算法的数值分解

实际上，VMD与维纳滤波紧密的联系表明，VMD算法具有更好的噪声处理效果。为证明它在定量检测和分离方面具有优异的性能，将分解结果与小波分解和EMD对比。小波分解采用Daubechies系列小波db5小波基进行五层分解。

2.1VMD噪声鲁棒性研究

为证明VMD的噪声鲁棒性，选取含噪声的合成输入信号进行分析，其各分量为2、20、300Hz共3个频段的余弦信号：

fn(t)=cos(4πt)+0.2cos(40πt)+0.02cos(600πt)+η

其中，η为加性高斯白噪声，噪声强度为0.01。

对比图1～4的数值模拟结果可知，VMD分解出的低中频部分模态函数能较好地还原原始信号，但高频部分存在一定的噪声干扰。由图5可知，各模态函数的中心频率为12.57、125.70、1 885.00Hz，能与原始信号较好地吻合。由图3(s=a5+d5+d4+d3+d2+d1)可知，当小波分解五层时与原始输入信号低频部分的吻合程度不如VMD，且第三层出现波形畸变，主要原因是调幅受到高频部分幅值的干扰发生畸变。由图4可知，原始4个分量的复合信号经EMD自适应分解为7个IMF分量和残余量，出现过度分解的现象。EMD可以分解出近似300.000Hz的高频分量(IMF1)、15.630Hz的中频部分(IMF2)和1.953Hz的低频部分(IMF4)，但IMF2与IMF3出现模态混叠，且低频部分出现严重的模态混叠。实际应用中，天然气管道泄漏信号为低频信号，用小波提取出所需要的特征频段存在一定难度，且准确性不高。因此从噪声抗干扰性来看，VMD比EMD和小波分解具有更好的噪声鲁棒性。

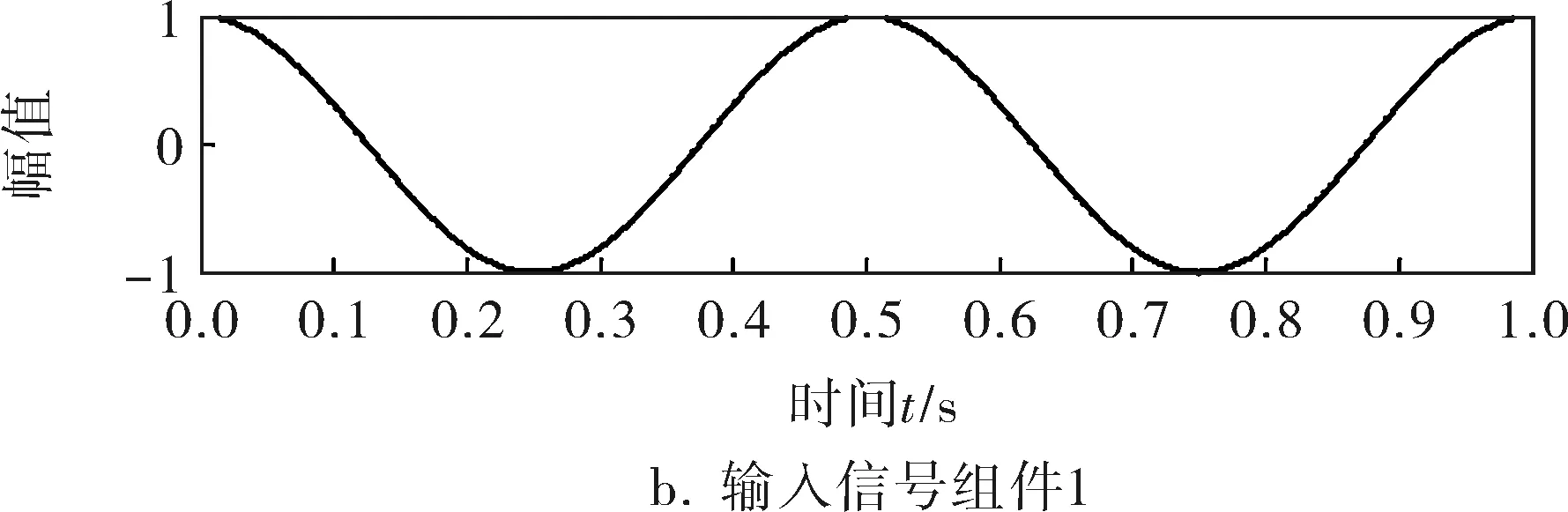
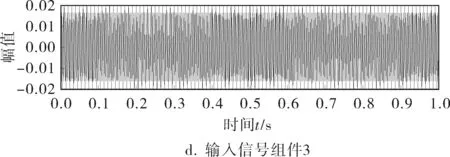
图1 原始输入信号

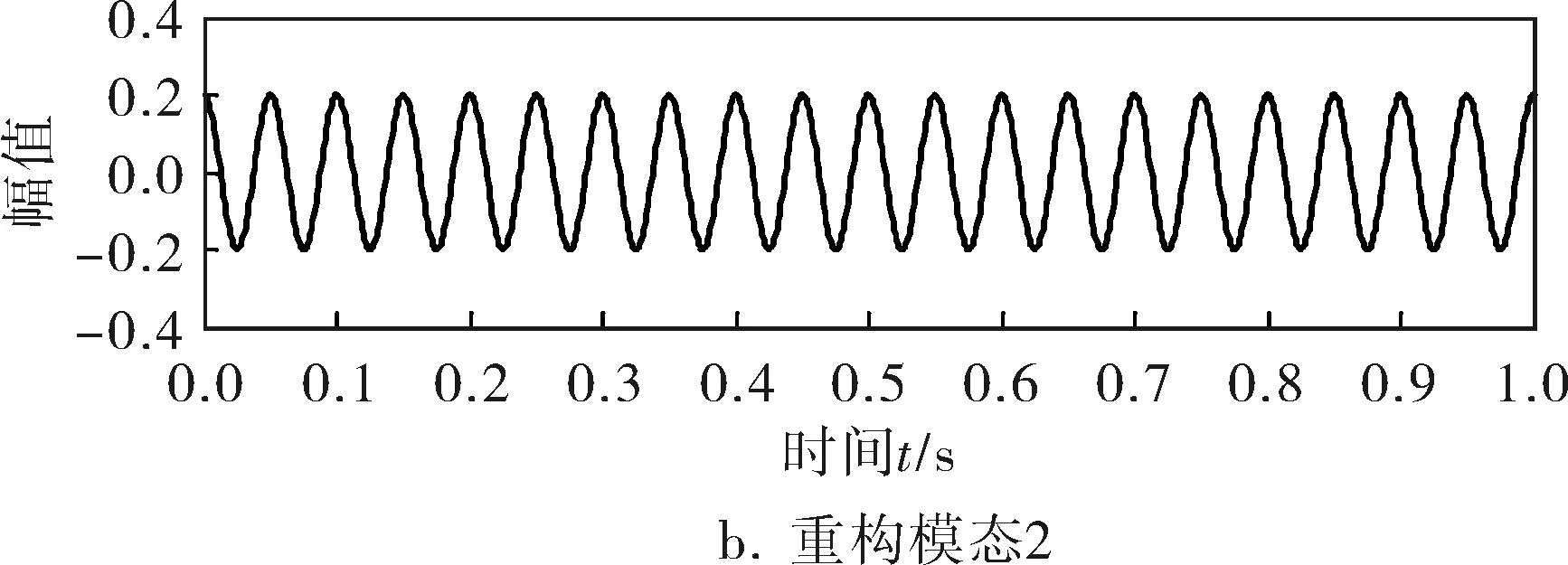
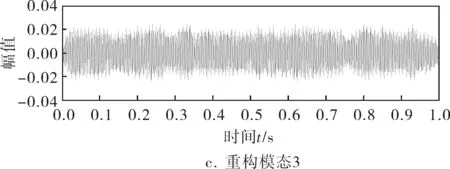
图2 VMD重构模态

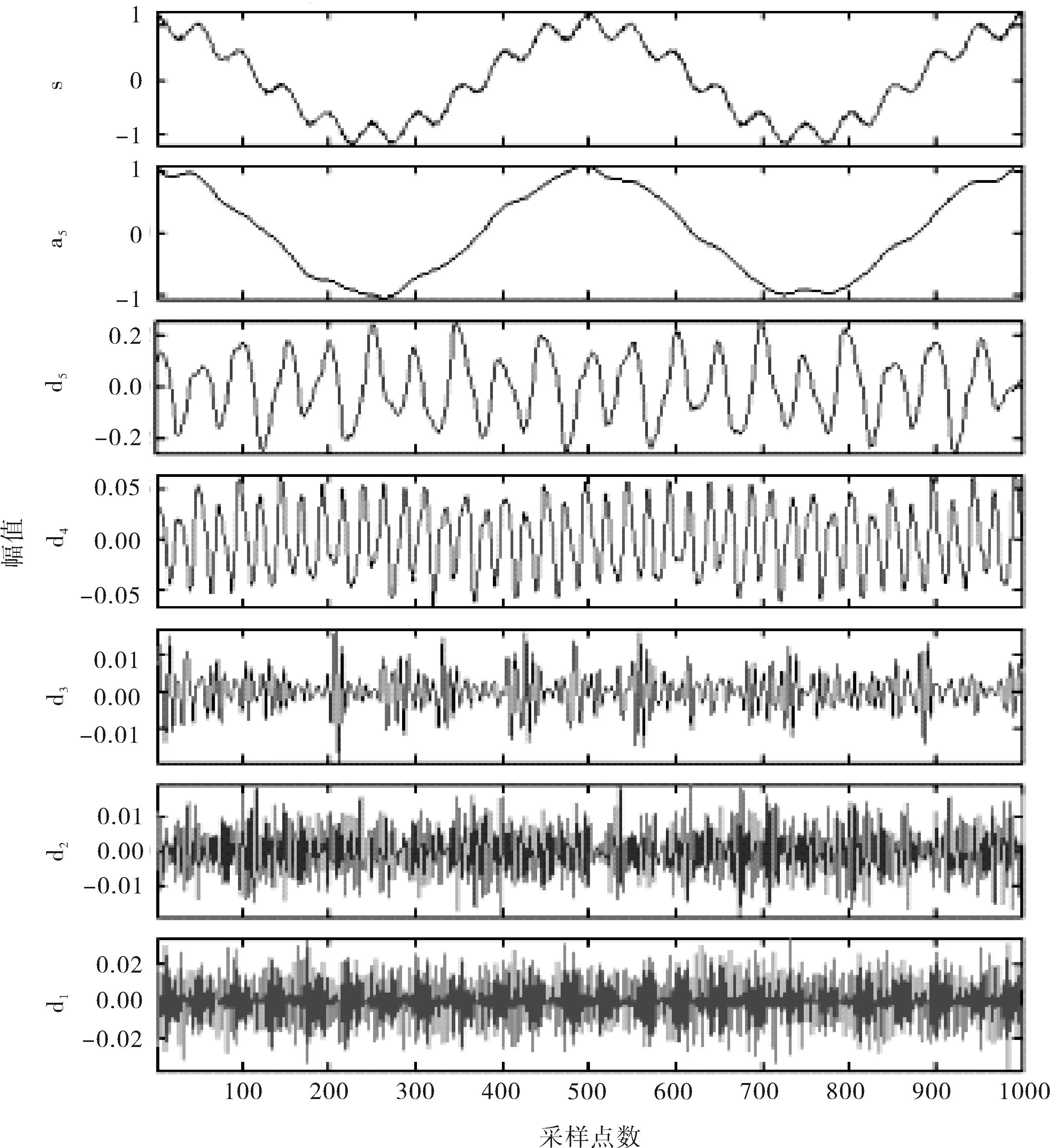
图3 小波分解

2.2VMD分解非平稳多模态信号

通过研究非平稳信号来验证VMD的分解效果，并与EMD和小波分解做比较。选用的输入信号为两个不同频率和幅值的锯齿波复合信号，不加干扰信号，小波分解用Daubechies系列小波db5小波基进行三层分解。复合输入信号fn(t)表达式为：

fn(t)=2×sawtooth(16πt)+0.5×sawtooth(200πt)

选择fn(t)复合输入信号(图6)来验证VMD分解，是因为其本征模态符合Huang的原始定义，但与VMD对IMF的新定义存在冲突。实际上，锯齿波的整个频谱都包含高次谐波，甚至含有模态混叠，而这是违反VMD模态的带宽限制规定的，而图7的分解结果证明，VMD能精确捕捉低频段的中心频率。虽然小波变换是处理非平稳信号的有力工具，但是由图8(s=a3+d3+d2+d1)可知，通过小波分解三层之后，仍然无法提取出需要的低频分量，且高次谐波存在于整个分解模态，各层细节信号出现严重的波形畸变，主要为调幅变化，在信号间断处出现明显的波形幅值跳变。图9的EMD分解将一个原本由两个分量复合的信号分解出7个IMF分量和一个残余量，出现了过度分解，且第一个IMF分量同小波分解一样出现了波形畸变，主要是幅值突变。因此在处理非平稳间断信号时，VMD具有更好的效果。

图8 小波分解

3 天然气管道泄漏信号检测与分析

天然气管道泄漏检测系统由硬件和软件构成，硬件部分通过各种传感器来采集与管道泄漏相关的物理数据，软件部分基于LabVIEW开发。检测系统实施流程为：LabVIEW设置采样频率为1kHz，由声感知设备采集信号，并将信号转送至工控机的采集卡，由Matlab将采集的信号数据进行VMD分解，然后对低频特征模态进行识别，判断是否发生泄漏[8]。由于管道微漏产生的噪声微弱，长距离的管道又使待检测信号衰减，且管道检测现场的环境复杂，因此现场采集的声发射信号有一定的噪声干扰。

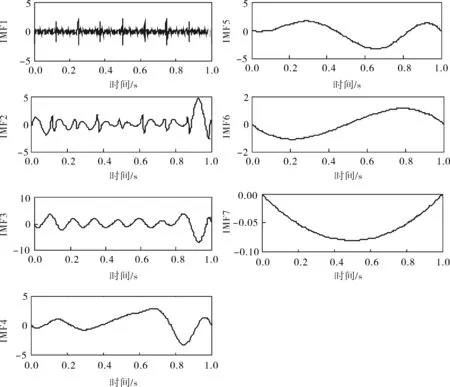
图9 EMD分解

图10为阀门转动两圈时管道的泄漏信号，由频谱分解(图11)可知，该信号为低频信号。对该信号进行预设尺度为3的VMD分解，3个模态的中心频率分别为8.46、424.60、525.10Hz，因管道泄漏信号为低于100Hz的低频信号，故对其他两个模态不做分析。图12的重构模态1明显地检测到了4圈漏气，也检测出了原始输入信号不明显的两次漏气，因此低频段模态重构能够更加明确地分析泄漏问题。图13(s=a8+d8+d7+d6+d5+d4+d3+d2+d1)的小波分解直至分解到八层时才出现所需低频信号的d8分量，其他各层均出现谐波干扰，且信噪比远不如VMD。如图14所示，EMD分解出了15个IMF分量和一个残余量，且出现了严重的模态混叠。

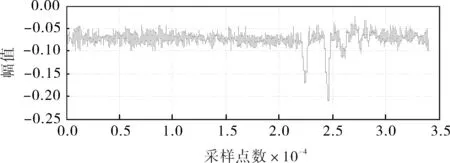
图10 管道泄漏信号

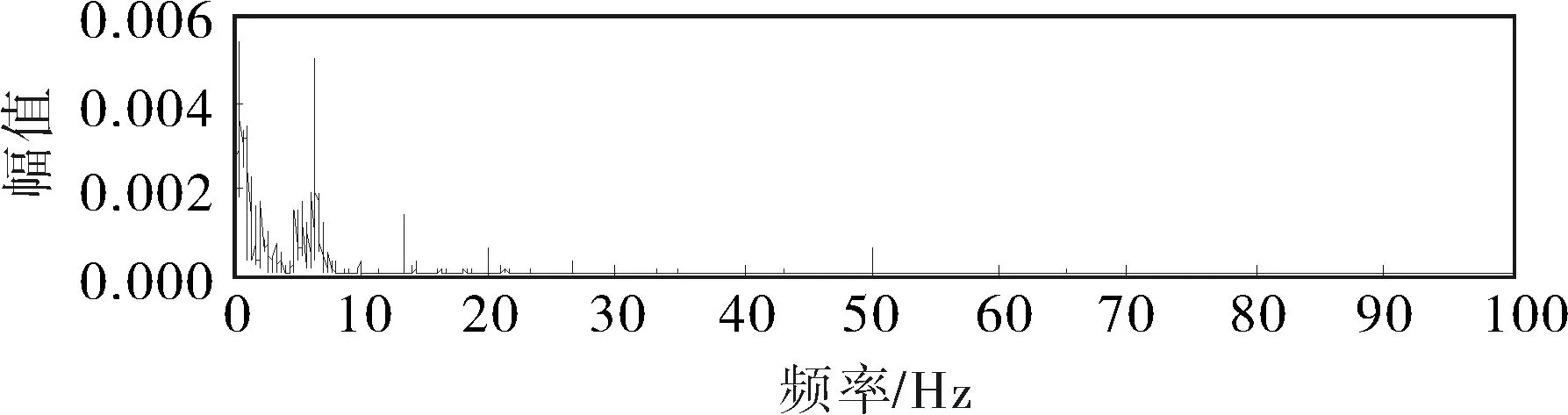
图11 泄漏信号频谱图

图12 VMD重构模态

图13 小波分解

图14 EMD分解

天然气管道泄漏信号为低频信号，将分解出的各低频分量重构后与原始信号的相关度用相关系数表示分别为0.926(VMD)和0.579(EMD)，可知VMD能较好地保留信号的主要组成成分——低频部分，具有更好的信号保真度，为后续的数据分析提供更为准确的数据基础。

从时域上看，VMD在分解3个模态函数时就可以分解出低频分量，而小波分解需要预先选择基函数，基函数的选取直接影响到信号分解结果，由于小波分解的基函数较多，需要对不同信号分别进行基函数讨论，因此对实际应用带来了一定影响。

4 结束语

笔者在介绍VMD算法的基础上，进一步研究了其信噪比与处理非平稳信号的能力，并与小波分解和EMD做了对比，发现VMD表现出了明显的优越性，尤其是抗干扰性和分离低频信号时，有着EMD和小波分解无可比拟的优势。将VMD应用于检测天然气管道泄漏信号时，用VMD分解含噪检测信号，提取低频模态特征，从时域上分析泄漏信号，相对于小波分解和EMD，VMD能够提供更准确的分析信号，验证了该算法在管道泄漏信号检测方面应用的可行性。由于VMD算法采用的是Weiner滤波器，因此在处理低频信号时具有突出的优势。但当输入信号噪声强度较大时，将对VMD的高频分解产生影响，同时其带宽限制、预设尺度及收敛条件等都需要进行更进一步的深入研究。

[1] 高炳坤,贾莹.基于声波的天然气管道泄漏检测与定位[J].化工自动化及仪表,2013,40(3):305～308.

[2] 李宏,申瑞琦.基于EMD和小波变换的热网管道泄漏检测与定位方法[J].化工自动化及仪表,2014,41(6):652～654.

[3] Dragomiretskiy K,Zosso D.Variational Mode Decomposition[J].IEEE Transactions on Signal Processing,2013, 62(3):531～544.

[4] 刘长良,武英杰,甄成刚.基于变分模态分解和模糊C均值聚类的滚动轴承故障诊断[J].中国电机工程学报,2015,35(13):3358～3365.

[5] Hahn S L.Hilbert Transforms in Signal Processing[M].Boston:Artech House Publish,1996.

[6] Huang N E,Shen Z,Long S R,et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Nonstationary Time Series Analysis[J].Proceeding of the Royal Society,1998,454(1971):903～995.

[7] 段家银,段天友,刘豪,等.变模态分解在微地震信号去噪中的应用[J].石化技术,2015,(7):217.

[8] 安连锁,冯强,沈国清,等.可变模式分解在炉膛压力管道微弱泄漏信号检测的应用研究[J].锅炉技术,2015,46(4):1～6.

VMDAlgorithmandItsApplicationinPipelineLeakageDetection

LU Jing-yi, MA Wen-ping, GAO Bing-kun, LIU Wei, GAO Wei

(SchoolofElectricalEngineering&Information,NortheastPetroleumUniversity,Daqing163318,China)

The application of variational mode decomposition (VMD) algorithm in the leakage signal detection of natural gas pipeline was investigated. Analyzing the noise robustness, over-decomposition and the unsaturated decomposition and then comparing the results to that of empirical mode decomposition (EMD) and wavelet decomposition can prove VMD algorithm’s feasibility and effectiveness in detecting and analyzing pipeline leakage signals,and VMD has better noise robustness and better effect in leakage signal detection.

pipeline leakage, VMD, EMD, wavelet decomposition, Matlab

2015-12-28(修改稿)

黑龙江省自然科学基金项目(E201332)

TQ055.8

A

1000-3932(2016)07-0694-08