双时滞线性切换正系统的鲁棒L1控制器设计

李艳辉 袁 帅

(东北石油大学电气信息工程学院，黑龙江 大庆 163318)

双时滞线性切换正系统的鲁棒L1控制器设计

李艳辉 袁 帅

(东北石油大学电气信息工程学院，黑龙江 大庆 163318)

设计了一类正系统在任意切换信号下的鲁棒L1控制器。针对一类带有状态时滞和输入时滞的线性切换正系统，基于线性余正Lyapunov-Krasovskii泛函和平均驻留时间理论，推导出在任意切换信号下使系统指数稳定且具有干扰抑制能力γ的充分条件，进一步设计了鲁棒L1控制器，保证系统不仅是指数稳定且具有干扰抑制能力γ。最后通过数值仿真示例证明了控制器的有效性。

L1控制器 线性切换正系统 平均驻留时间 指数稳定

正系统是一类状态非负的系统，在化工、工业工程、生态学、生物医学、经济学及人口模型等领域中较为常见。目前，正系统的分析和综合成为一个热点课题，吸引了国内外学者的关注[1～3]。然而在工程背景下，时滞普遍存在，使系统性能变差，因此时滞系统的研究就变得具有实际意义。关于时滞系统的分析和综合，众研究者取得了一些成果[4]。张会珍等针对多时滞系统设计了鲁棒容错控制器[5]；Zhu S等研究了时滞正系统的指数稳定性的判据[6]；Aleksandrov A Y和Mason O基于Lyapunov-Krasovskii泛函，研究了时滞离散正系统的稳定性[7]。

切换系统中一般含有多个子系统，若子系统均为正系统，则此类系统称为切换正系统，此类系统在编队飞行、通信系统中具有重要的研究价值。Du H和Liu Y Z基于余正Lyapunov函数与平均驻留时间理论，得到了切换正系统渐近稳定的充分条件[8]；翟世东和杨晓松针对时滞离散分段线性正系统，给出系统渐近稳定的充分条件[9]；Chen X M等分析了离散正系统的渐近稳定性，并通过迭代优化算法设计了满足L1性能的控制器[10]。然而在网络系统、通信系统中时滞可能不唯一，所以研究双时滞正系统就具有了重要意义，而且关于双时滞线性切换正系统方面的研究很少，因此笔者针对该类系统，利用线性余正Lyapunov-Krasovskii泛函和平均驻留时间理论，给出系统指数稳定且具有抑制干扰能力γ的充分条件，并将此条件转化为线性规划问题，然后设计鲁棒L1控制器使系统不仅是指数稳定的且具有抑制干扰能力γ，最后通过仿真实例验证了控制器的有效性。

1 问题描述①

考虑如下双时滞线性切换正系统：

(1)

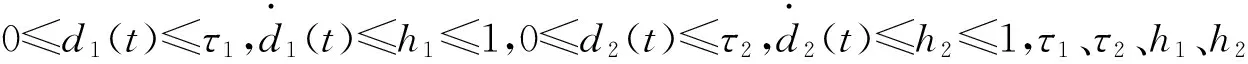
通过状态反馈控制u(t)=Kpx(t)，闭环系统变为：

(2)

笔者的目标是设计一个鲁棒L1控制器，使得系统(2)满足以下两个条件：

a. 系统(1)是指数稳定的；

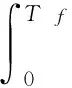
注1：由于系统是切换系统，所以设计模态依赖的控制器，即针对每个切换子系统都对应不同的控制器，这样可以降低控制器的局限性。

定义1 一个实矩阵A，对角线元素是任意的，非对角线元素为非负的，则称该矩阵为Metzler矩阵。

引理1 当且仅当矩阵Ai(i∈N)为Metzler矩阵，且Adi≥0时，该系统为正系统。

定义2 考虑一个切换系统，如果存在切换信号σ=σ(t)，使得系统的轨迹满足‖x(t)‖≤a‖x(t0)‖cle-β(t-t0),其中‖x(t0)‖cl=sup-τ≤θ≤0x(t0+θ),α≥1,β>0,t≥t0，则称该系统是指数稳定的。

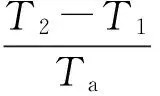
2 系统的指数稳定性和L1性能判据

下面考虑双时滞线性切换正系统，给出L1性能判据。

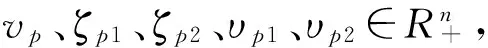
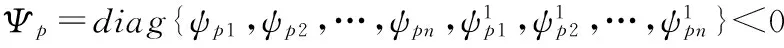
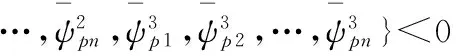
(3)

(4)

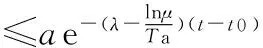
(5)

常数μ≥1满足vi≤μvj,ζ1i≤μζ1j,υ1i≤υ1j,ζ2i≤μζ2j,υ2i≤υ2j,∀i,j∈N

(6)

则对任意切换信号σ(t)，系统(2)是指数稳定的，且具有鲁棒L1抑制干扰能力γ。

证明 当ω=0时，选择如下形式的线性余正Lyapunov-Krasovskii泛函：

Vp(t)=Vp1(t)+Vp2(t)+Vp3(t)+Vp4(t)+Vp5(t)

(7)

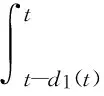
对泛函(7)进行求导并进行整理可得：

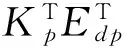
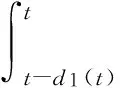
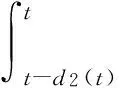
根据条件(3)可得不等式：

又因为-e-λτ1υp1≤0、-e-λτ2υp2≤0,可得到：

Vp(t)+λVp(t)≤0

(8)

假设t0,t1,…,tk为[t0,t)的切换时刻，对式(8)两边同时积分可得：

Vσ(t)≤e-λ(t-ti)Vσ(ti)(ti)，∀t∈[ti,ti+1),i=0,1,…,k-1

(9)

由式(6)和给出的线性余正Lyapunov-Krasovskii泛函(7)可得：

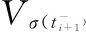
(10)

根据式(4)、(9)、(10)和k≤(t-t0)/Ta，在区间[t0,t)上：

μVσ(tk-1)(tk-1)=e-λ(t-tk-1)μVσ(tk-1)≤…

(11)

由Vσ(t)(t)的定义，可得：

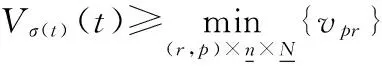
(12)

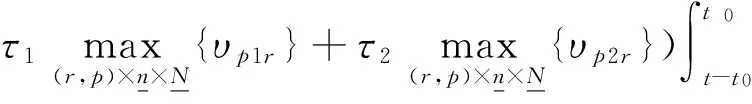
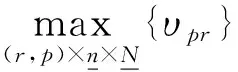
(13)

由于系统状态满足定义(2)，所以系统是指数稳定的。

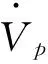
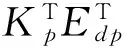
(14)

其中，I=[1,1,…,1]T，根据式(3)可得：

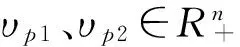
对于∀p∈N，由以上6个不等式可知：

整机面板只有两个操控按键，分为清洗和复位键，使用期间最好每月进行一次清洗作业，更能使净水器保持持续的良好运转。

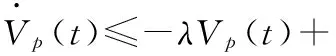
(15)

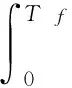
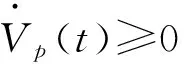
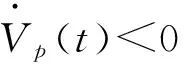
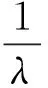
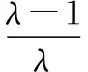
由式(3)知J<0，因此可以进一步推导出：

(16)

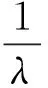
定理1得证。

注2：正系统的状态都是在非负象限内，研究L1性能更能说明系统的特性，系统稳定都需要一定的时间，指数稳定可以加快系统稳定的速率。

3 系统的鲁棒L1状态反馈控制器设计

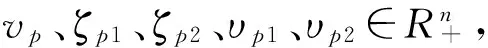
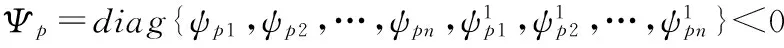
(17)

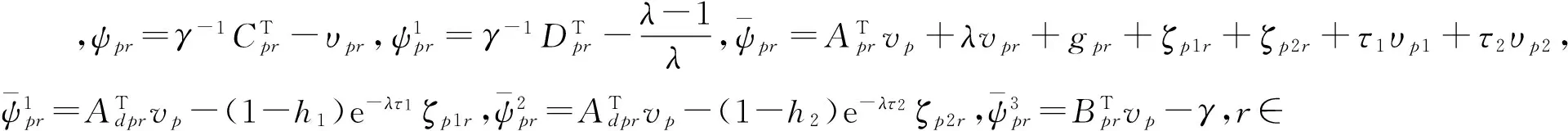
注3：针对本系统，不要求开环系统为正系统，即A矩阵可以不是Metzler矩阵，只需要保证在控制加上之后，闭环系统是正系统，则可保证系统的鲁棒L1性能。

算法步骤如下：

a. 给定常数矩阵Ap、Adp、Ep、Edp、Bp、Cp、Dp，∀p∈N设定初始值；

b. 给一个常数λ，通过解不等式(17)可求得vp、gp、ζp1、ζp2、υp1、υp2、γ；

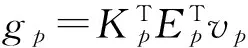
d. 得出最终的控制器增益Kp，并构造反馈控制器u(t)=Kpx(t)。

4 数值例子

考虑式(1)的系统，描述如下：

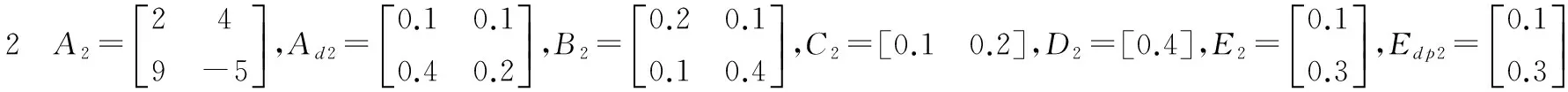
时变时滞d1(t)=0.5|sin(0.2t)|，d2(t)=0.4|sin(0.1t)|

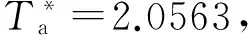
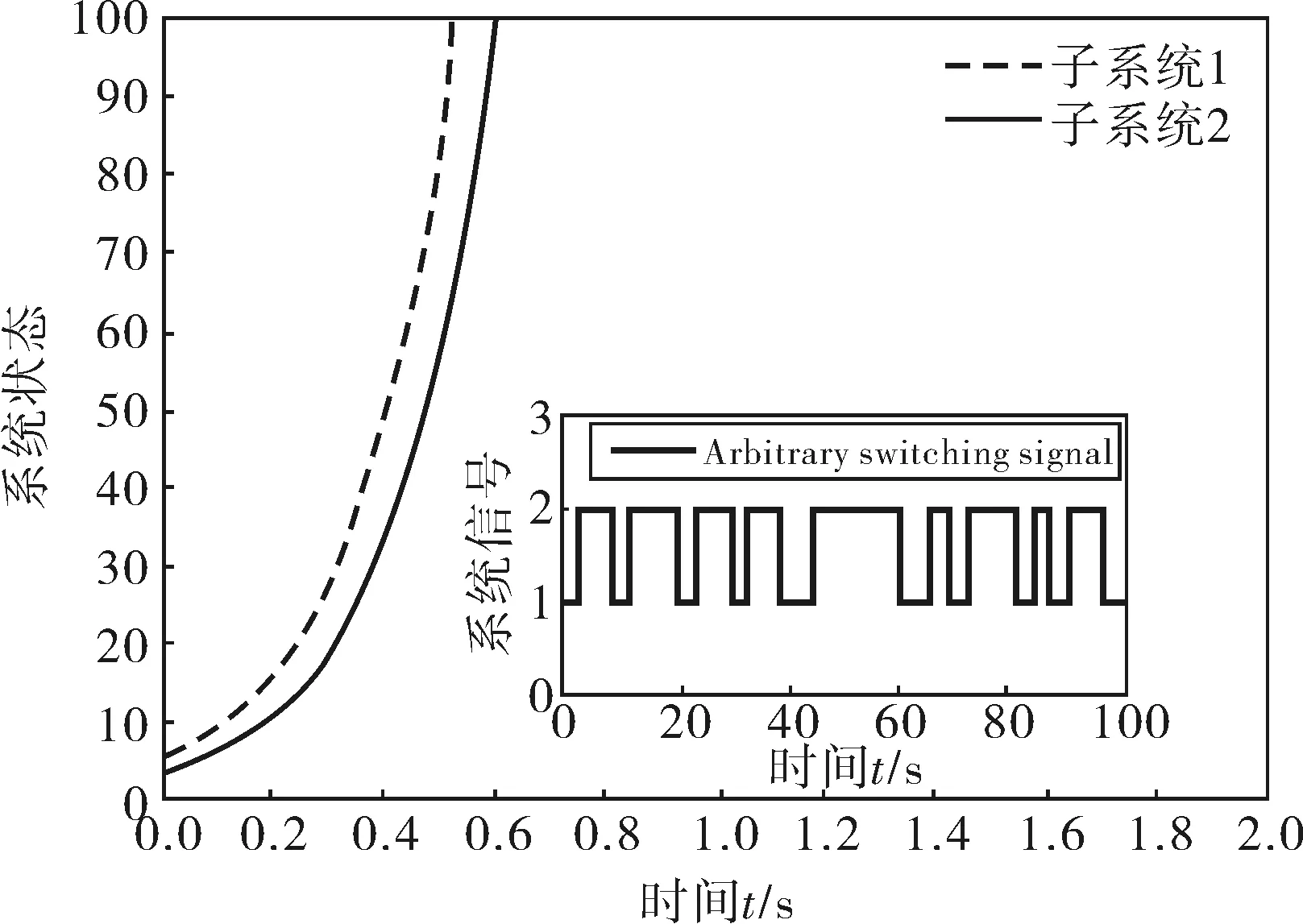
图1 任意切换信号下的开环状态响应曲线

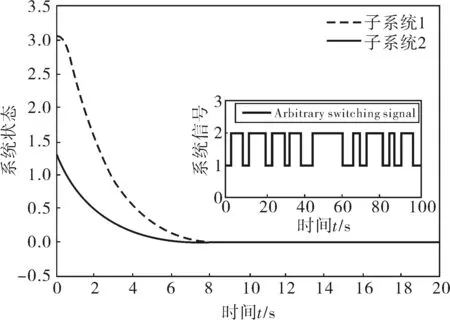
图2 任意切换信号下的闭环状态响应曲线

注4：从图1、2可以看出，信号是满足平均驻留时间的随机信号；从图1可以看出，开环系统以指数形式快速发散，而在加了控制器后，闭环系统在短时间内快速收敛，使系统达到稳定。

5 结束语

笔者针对一类具有状态时滞和输入时滞的线性切换正系统去设计鲁棒L1控制器。基于线性余正Lyapunov-Krasovskii泛函和平均驻留时间理论，先给出使双时滞线性切换正系统指数稳定的充分条件，之后给出该系统的状态反馈控制器设计方法，并使该鲁棒L1控制器有干扰抑制能力γ，最后通过数值仿真实例证明了控制器的有效性。

[1] 段良婧.正系统的H∞降阶滤波器的设计[D].临汾：山西师范大学,2012.

[2] Rami M A.Solvability of Static Output-feedback Stabilization for LTI Positive Systems[J].Systems and Control Letters,2011,60(9):704～708.

[3] 宋世君,冯俊娥，孟敏.受控正系统的弹性静态输出反馈鲁棒H∞控制[J].控制理论与应用,2014,31(5):671～676.

[4] Zhu S Q,Meng M,Zhang C H.Exponential Stability for Positive Systems with Bounded Time-varying Delays and Static Output Feedback Stabilization[J].Journal of the Franklin Institute,2013,350(3):617～636.

[5] 张会珍,王德平,邵克勇,等.一类不确定多时滞系统的鲁棒容错控制研究[J].化工自动化及仪表,2013,40(7):831～833.

[6] Zhu S,Li Z,Zhang C H.Exponential Stability Analysis for Positive Systems with Delays[J].IET Control Theory and Applications,2012,6(6):761～767.

[7] Aleksandrov A Y,Mason O.Diagonal Lyapunov-Krasovskii Functional for Discrete-time Positive Systems with Delay[J].Systems & Control Letters,2014,63(1):63～67.

[8] Du H,Liu Y Z.Stability Analysis for Continuous-time Switched Positive Linear Systems[J].Journal of Shenyang Normal University,2015,33(2):192～196.

[9] 翟世东,杨晓松.离散分段线性时滞正系统的稳定性分析[J].动力学与控制学报,2010,8(4):346～349.

[10] Chen X M, Lam J, Li P,et al.L1-induced Norm and Controller Synthesis of Positive System[J].Automatica,2013,49(5):1377～1385.

RobustL1ControllerDesignforLinearSwitchedPositiveSystemswithDoubleDelays

LI Yan-hui, YUAN Shuai

(SchoolofElectricalEngineeringandInformation,NortheastPetroleumUniversity,Daqing163318,China)

The robustL1controller for a class of positive systems under arbitrary switching signal was designed. Aiming at linear switched positive systems with state delay and input delay, having linear co-positive Lyapunov-Krasovskii functional and average residence time theory based to derive sufficient conditions for the system’s exponential stability and the ability to suppress interferenceγunder arbitrary switching signals was implemented so that robustL1controller designed can guarantee the system’s exponential stability and ability of anti-interferenceγ. Numerical simulation proves effectiveness of this controller.

L1controller,linear switched positive system, average residence time, exponential stability

2015-11-16(修改稿)

空间智能控制技术国家级重点实验室开放基金项目(002008834000)；黑龙江省自然科学基金项目(F201403)；黑龙江省博士后科学研究发展基金项目(LBH-Q13177)；东北石油大学培育基金项目(XN2014112)

TP273

A

1000-3932(2016)07-0671-05