基于排队论的急诊留观系统床位配置优化研究
2016-11-22马秋月
马秋月
·研究与实践·
基于排队论的急诊留观系统床位配置优化研究
马秋月
为了有效解决急诊留观系统中病人等待时间过长的问题,建立了急诊病人转移过程中的排队模型,并在考虑了急诊病人滞留现象对所在阶段服务效率的影响后,提出了更准确的计算病人等待时间的方法,并将其应用于床位资源的再分配中。通过实例分析,表明所提算法可确定床位的最优配置,有效减少急诊病人的等待时间。
排队论;急诊管理;病人滞留;床位配置
我国的医疗资源短缺问题愈发严峻,尤其是负责紧急、危重病人救治工作的急诊科,长期处于高负荷状态,造成急诊病人的等待,从而无法获得及时的诊疗。急诊病人等待时间过长是急诊留观系统面临的一个主要问题。通过实际调查发现,留观室存在较为严重的病人滞留现象,即急诊病人由于转入阶段无可用床位而继续停留在当前阶段的现象[1]。不同科室的负荷强度是存在差异的,有的科室负荷大、床位资源紧缺,而有的科室则长期剩有空闲床位。这种不合理的床位资源分配会加剧病人的滞留现象。针对病人在急诊系统中的流动情况,有研究者[2-3]通过建立排队模型,确定了各住院科室床位数量对病人等待时间的影响。由此可见,住院科室床位资源的优化配置对于缓解急诊病人滞留现象意义重大。目前,已有学者[4-6]利用排队论理论建立病人排队模型,以优化各科室的床位资源配置,进而缓解滞留现象,但其均未考虑病人滞留对所在阶段服务效率的影响。
本文对病人等待进入留观室进而转入住院科室这一流程建立排队模型,考虑病人滞留对所在阶段服务效率的影响,以期更准确地计算病人平均等待时间,并在此基础上,对住院科室的床位数量进行优化配置,以有效缓解滞留现象及减少急诊病人等待时间。
1 系统描述及建模
对留观室至住院科室这一急诊留观系统进行研究,如图1所示。急诊病人会以λ0的速率到达留观室,在留观室接受服务后,会根据自身的病情转入相应的科室、离开医院或是死亡。由于考虑过多的病人流向意义不大,因此,本文选取病人流入比率较大的两个科室为代表,设置概率分别为P1、P2,将所有其他病人流向的概率汇总为P3。而对于住院科室来说,除了来自留观室的急诊病人外,其还会接收普通住院病人,设置两个科室的普通病人到达率分别为λ1和λ2。
2 床位配置优化方案
本文主要研究急诊病人等待时间过长的问题,而导致该问题的一个关键原因在于床位不可用使得急诊病人发生滞留。急诊病人在完成留观室的服务后,由于下游科室的床位不可用, 从而滞留在留观室中,继续占用留观室床位,进而使得其他急诊病人不能及时进入留观室。当然,增设各科室的床位可有效地改善这一现象,但由于医院空间及投入成本等各因素的限制,这种方案的可行性不高。因此,本文从医疗资源配置优化的角度进行研究。在实际调查中发现,急诊留观系统中各科室的负荷强度具有差异,部分科室长期人满为患,而部分科室始终存在空余床位,这种床位资源分配不合理会加剧滞留现象,进而导致急诊病人等待时间过长。因此,本文以病人等待时间为指标来衡量各科室床位资源配置的合理性,建立床位配置优化方案,如图 5 所示。

图5 床位配置优化方案
我们拟定在原有床位资源总量不变的条件下,对各科室的床位进行再分配,以确定病人等待时间最短时最佳的床位配置。由计算公式可知,病人等待时间由到达率、服务效率及床位数量 3 个参数决定,而病人的滞留会导致其所在阶段的服务效率发生变化,因此,提出的公式(10)可更准确地计算病人的等待时间。基于此,保持总床位数量不变,可通过改变各科室的床位配比,计算不同床位配置下病人的等待时间,来确定病人等待时间最短时最优的床位配置,进而实现病人等待时间的有效减少。
3 实例分析
我们以天津某医院的急诊留观系统为研究背景,数据收集通过实际调查、询问医护人员 及采集病人住院记录信息等方式进行。首先对获取的数据进行处理,剔除异常数据,然后统 计分析有效数据,得到模型所需参数,见表 1。

表1 参数汇总
利用公式(3)(4)输入相关参数即可得到急诊病人等待进入科室的时间,而急诊病人等待进入留观室的时间可通过公式(9)(10)计算获得。本文的研究方案是通过改善科室间床位分配比例以降低急诊病人等待时间。在其他输入参数不变的条件下,保持两科室总床位数为60 不变,调整两科室床位配比,计算得到不同床位配置下,急诊病人等待进入留观室与住院科室的时间,见表 2。
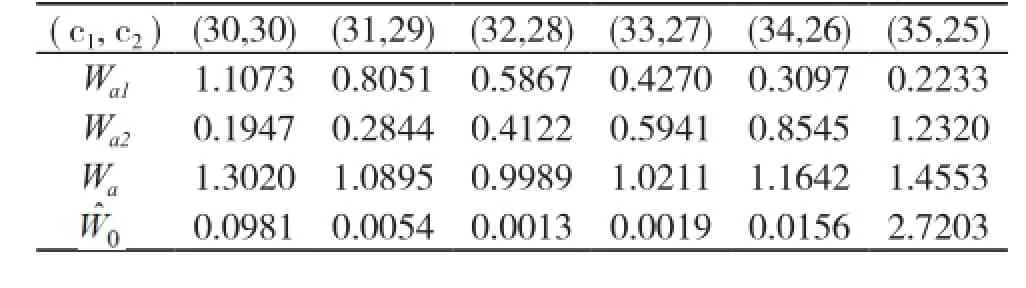
表2 不同床位配置下急诊病人的等待时间(天)
由表2可知,当两科室的床位分别为32, 28时,急诊病人等待进入留观室的时间与等待进入科室的时间均最短,分别为0.0013天、0.9989天。为更好地分析急诊病人等待时间随科室床位配置的变化规律,将上述结果转化成为曲线图,如图6所示。

图6 急诊等待时间随科室床位配置变化情况
由图6可知,急诊病人等待进入留观室与住院科室的时间均呈现先降低后增加的趋势,表明科室的床位配置存在最优值,因此,要对各科室的床位数量进行再分配,确保床位配置处于最优状态,实现急诊病人等待时间的有效减少。
目前两科室的床位数量分别为35, 25,急诊病人等待进入留观室的时间为2.7203天,等待进入科室的时间为1.4554天,而计算不同床位配置下病人的等待时间后,可知当两科室的床位数量分别为32, 28时,急诊病人等待进入留观室与科室的时间分别降为0.0013天、0.9989天,见表3。

表3 改善前后结果对比(天)
对比可知,将两科室的床位配置由(35, 25)变为(32, 28)后,急诊病人进入留观室的等待时间可减少约2.7天,进入科室的等待时间可减少约0.5天,由此可见,其改善效果非常明显。
4 结论
此文研究了留观室前急诊病人等待时间过长的问题,考虑了病人滞留对所在阶段服务效率的影响,提出了更准确的计算病人等待时间的方法,并以此为基础,对住院科室的床位进行再分配,获得以病人等待时间最短为目标的最优床位配置。
将本文的研究方法应用于实际的医疗系统中,结果表明,在不增加医疗资源投入的前提下,改善当前的科室床位资源配比,可使急诊病人等待进入留观室与科室的时间分别降低2.7天、0.5天,具有良好的改善效果。这种不增加投入的前提下,优化相关参数的配置,实现系统运行效率有效提升的研究方法具有较重大的意义。
在后续的研究中,可从下面3个方面对本研究进行扩展:第一,可考虑各科室之间病人的转移;第二,可考虑等待进入留观室的急诊病人优先权问题;第三,可建立更具有一般性的排队模型。
[1] Bretthauer KM, Heese HS, Pun H, et al. Blocking in healthcare operations: a new heuristic and an application[J]. Production and Operations Management, 2011, 20(3) : 375-391.
[2] Seshaiah CV, Thiagaraj HB. A queueing network congestion model in hospitals[J]. European Journal of Scientific Research, 2011, 63(3) : 419-427.
[3] Kusum SM, Elisa F. A conceptual framework for improving critical care patient flow and bed use[J]. Annals of the American Thoracic Society, 2015, 12(6) : 886-894.
[4] Cochran JK, Bharti A. A multi-stage stochastic methodology for whole hospital bed planning under peak loading[J]. International Journal of Industrial and Systems Engineering, 2006, 1(1) : 8-36.
[5] Lin D, Labeau F. Estimating the waiting time of multi-priority emergency patients with downstream blocking[J]. Health Care Management Science, 2014, 17(1) : 88-99.
[6] 周文正.排队论模型在医疗服务系统中的应用研究[D].武汉:华中科技大学,2011.
[7] Gross D, Harris C. Fundamentals of queueing theory[M]. New York: John Wiley & Sons, 1998.
[8] Eman Almehdawe. Queueing network models of ambulance offload delays[D]. Canada: University of Waterloo, 2012.
[9] Koizumi N, Kuno E, Smith TE. Modeling patient flows using a queuing network with blocking[J]. Health Care Management Science, 2005, 8(1) : 49-60.
Study on the optimization of bed allocation in the emergency observation system based on queuing theory
Ma Qiuyue. Hebei University of Technology, Tianjin 300401, China
In order to effectively solve the problem of too long waiting of patients in the emergency observation system, a queuing model in the transfer process of emergency patients is built, and after taking into account the impact of emergency patients' detention phenomenon on the service efficiency in the corresponding stage, a more accurate method for calculating the waiting time of a patient is put forward and applied in the reallocation of bed resource. Example analysis demonstrates that the proposed algorithm is able to determine the optimal allocation of beds and effectively reduce the waiting time of emergency patients.
Queuing theory; Emergency treatment management; Patients' blocking; Bed allocation
10.3969/j.issn.2095-7432.2016.05.008
300401 天津,河北工业大学

图1 急诊留观系统服务流程
为了更详细描述该急诊留观系统,先将其分为留观室子系统与科室子系统,其流程见图2、图3。根据排队论建立病人等待时间与等待队长的算法,再对病人在两子系统间转移的时间交互关系进行说明,并在此基础上建立考虑滞留影响的病人等待时间算法。

图2 留观室子系统流程
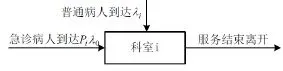
图3 科室子系统流程
1.1留观室子系统
在留观室子系统中,为获得等待进入留观室的急诊病人数量,假定留观室前存在无限等待空间,建立多服务窗等待制排队模型 M/M/n,急诊病人到达率为 λ0,各床位服务率为 μ0,床位数量为 c0。此时等待进入留观室的急诊病人数量 L0为[7]:

其中ω0=λ0μ0,ρ0=ω0c0<1(系统呈现稳态的必要条件)。
根据 Little 公式,急诊病人等待进入留观室的平均时间W0为W0= L0/λ0,即:
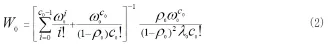
1.2科室子系统
在科室子系统中,住院科室 i 的病人流由急诊病人流和普通病人流两部分组成,急诊病人流的到达率为Piλ0,普通病人流的到达率为λi,一般情况下,急诊病人病情更为紧急,设定急诊病人流的优先权高于普通病人流,并为非强占式优先权。科室的床位数量为 ci,各床位服务率为 μi。仍将该子系统中病人的等待设定为多服务窗等待制排队模型 M/M/n。
急诊病人等待进入科室i 的平均时间Wai为[8]:

其中ωi=piλ0/ciμi,ρi=(piλ0+λi)/ciμi,i=1,2则急诊病人等待进入科室的平均时间Wa为:

普通病人等待进入科室i 的平均时间Wwi为:

其中ωi=piλ0/ ciμi, ρi=(piλ0+λi)/ciμi, i=1,2
根据Little公式,可求得急诊病人等待进入科室i的平均队长Lai为Lai= piλ0Wai,即:

则急诊病人等待进入科室的平均队长 La为:

普通病人等待进入科室i的平均队长Lwi为Lwi=λiWwi即:
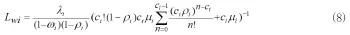
1.3急诊留观系统
病人完成留观室的服务后若转入科室无可用床位,则会被滞留在留观室,占用留观室的床位,而病人的滞留现象则会对留观室的服务效率产生影响。为量化滞留对服务效率的影响, 引入实际服务时间的概念[9],即留观室的服务时间与病人滞留时间之和,如图 4 所示。

图4 留观服务时间表示

其中,Wa可由公式(3)(4)计算。
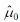
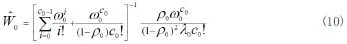

其中ω0=λ0(1/μ0+Wa) ,ρ0=ω0/ c0
(2016-08-01)
