基于Logistic函数的社会化矩阵分解推荐算法

郭云飞， 方耀宁， 扈红超

(国家数字交换系统工程技术研究中心， 河南，郑州 450002)



基于Logistic函数的社会化矩阵分解推荐算法

郭云飞， 方耀宁， 扈红超

(国家数字交换系统工程技术研究中心， 河南，郑州 450002)

持续指数增长的互联网逐渐带来了信息过载问题，使得推荐系统提供的信息过滤服务尤为重要. 协同过滤是推荐系统领域最为成功的技术，但依然存在数据稀疏性等问题. 社会关系信息能够有效提高推荐系统的预测准确性. 为解决数据稀疏性问题，本文提出了一种利用Logistic函数的社会化矩阵分解推荐算法. 在3组真实数据结合上的实验结果表明，本文提出的算法能够提供更准确的推荐结果，特别是在数据稀疏的情况下，显著缓解了数据稀疏性问题.

推荐系统；协同过滤；矩阵分解；社会关系；Logistic 函数

互联网的飞速发展将人类带入了信息爆炸的时代，人们经历了从信息匮乏到泛滥的剧变，发现从海量互联网信息中获取所需内容却成了一件复杂的事情——信息过载(information overload). 传统的搜索引擎只能被动提供无差别的搜索服务，而推荐系统利用数据挖掘、人工智能等技术能够主动帮助人们过滤信息，提供个性化服务[1-2]. 在过去的十多年里，推荐系统在电子商务网站、社交网络中大量涌现，正在引领人类进入一个多元化、个性化的网络新时代. 推荐系统不仅可以提供娱乐、生活方面的服务推荐，如网页、电影、好友等；而且可以提供更加专业化的推荐，如图书、论文、专利技术等[2-3].

协同过滤推荐算法在学术界和工业界都有了长足的发展，新的算法和研究热点不断涌现[2-3]. 其中，基于矩阵分解的推荐算法在预测准确性和稳定性上显示出较大优势，得到最为广泛的认可[4-6]. 矩阵分解推荐算法把评分矩阵看作是低秩矩阵，并分解成用户和项目两个低维特征矩阵的乘积，从而对未知评分进行预测. 虽然，矩阵分解算法的预测准确性较高，但依然面临着数据稀疏性等问题.

社会关系网络连接着人类社会与网络空间，正在逐渐模糊现实与虚拟的界限. 社交网络中以社会关系为纽带自发形成的群组，与现实社会中“物以类聚，人以群分”的原理一致. 社交网络能够详细记录用户历史行为信息，这就为分析用户行为特征，预测用户行为提供了数据基础. 对社会关系进行挖掘，可以估计出用户间的信任程度，有望解决推荐系统中的冷启动、数据稀疏性等问题[5-6].

本文围绕如何利用社会关系来解决数据稀疏性问题进行研究，提出一种基于Logistic函数的社会化矩阵分解推荐算法(logistic social matrix factorization, LSMF). LSMF算法根据社会关系建立简单高效的好友信任度评估机制，保证用户特征因子与好友特征因子相近，并利用Logistic函数对特征因子进行非线性映射. 在3种真实数据集合上的实验表明，LSMF算法能够明显降低预测误差(约5% RMSE)，缓解数据稀疏性问题.

1 LSMF算法

1.1 LSMF模型

LSMF(logistic social matrix factorization)从Logistic函数的使用和信任度计算两个方面对Social MF模型进行了改进[7-8]，如图1所示.

Logistic(g(x)=1/(1+e-x))定义域为(-∞，+∞)，值域为(0，1). Logistic函数在定义域内呈现出先缓慢增长，然后加速增长，最后逐渐稳定的趋势，能够较好反映生物种群发展、神经元非线性感知、人类认知学习过程等.

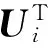
(1)

(2)

(3)

Logistic函数实现对特征因子非线性映射. 与Social MF模型相同， LSMF模型中用户的特征因子与均值为0的高斯分布正相关，保证特征因子的取值接近0以防止过拟合. 同时，用户的特征因子与好友特征因子的加权平均值正相关，即

(4)

于是，已知评分矩阵R和社会关系矩阵T，根据贝叶斯公式可以计算出用户和项目特征因子U，V，P和Q的后验概率为

(5)

对上式取对数，得到

(6)

(7)

为了减少正则化系数的个数，通常设定λU=λV，λP=λQ. β为社会化影响因子，β越大表示好友对目标用户的影响力越大，β=0时，模型退化为利用Logistic函数的矩阵分解推荐算法. 与矩阵分解推荐算法一样[5-6]，可以用随机梯度下降法方便地求解式(7).

1.2 信任度计算

“信任”是一个跨学科的概念，在不同领域的具体阐释会有不同. 信任度将“信任”量化，常用来衡量被信任者对目标用户影响程度的大小. 由于网络环境的复杂性、随机性、不确定性以及应用场景的多样性，社交网络好友间信任度的评估并不是一个简单的课题. 信任度的计算是搜索引擎、推荐系统领域的重要研究内容之一. 基于信任度计算的社会化推荐算法能够缓解协同过滤算法中的数据稀疏性问题，不同应用场景下信任度的计算方法也有很大区别[8].

SocialMF中所有好友具有相同的权值，表示不同好友对目标用户的影响力相同. 这种方法显然是不合理的，因为社会关系中包含了不同的社交圈，不同社交圈的兴趣爱好不同；而且，相同社交圈中的不同用户对于其他用户的影响力也是不同的.

一种直观的假设是，目标用户对好友的信任度与他们共同选择过的项目数量正相关. 因为只要用户i选择了项目j，无论评分是高还是低，都表示用户i对项目j这种类型的事物感兴趣，这是一种含蓄的反馈信息. 与基于评分相似性的信任度计算方法不同，本文采用一种简单高效的方法：

(8)

式中：nik为用户i和用户k共同选择过的项目个数；n0是赋值给所有好友的基础权值.n0=0表示只有共同评分过的好友才对目标用户有影响力，且正相关于共同选择过的项目个数；n0>0表示所有好友都对目标用户有影响力. 进一步对信任度矩阵T进行归一化处理，使得T的行和为1.

1.3 复杂度分析

2 实验设计及结果分析

2.1 数据集合及评价标准

为了测试LSMF算法的有效性，本文采用Epinions、Netflix和MovieLens1M三种推荐系统中最为常用的真实数据作为测试集合.

Epinions数据集合包含了49 290名用户对139 783个项目的664 824条评分和487 181条用户间的信任关系.Netflix数据集合是NetflixPrize比赛中使用的标准测试数据集，本文从中随机抽取了包含8 662名用户对3 000部视频的约30万条评分信息作为测试集合，不包含社会连接信息.MovieLens1M数据集合由GroupLens提供，包含了6 039名用户对3 883部电影的一百多万条评分信息.

Netflix和MovieLens1M数据集合中未提供社会连接信息，可以用于测试LSMF算法β=0的情况，以证明本文提出的Logistic映射方法能够有效提高预测准确性. 采用检验推荐算法最常用的预测误差RMSE作为评价依据，预测误差越小则表示算法性能越好.

(9)

式中：Stest为测试集合；|Stest|为Stest中的元素个数.

2.2 实验设计

本文设计了4组实验从不同方面对LSMF算法进行测试. A组实验较为全面对比MF、Social MF、LSMF三种算法的预测准确性；B组实验测试社会化影响因子β的取值对LSMF算法性能的影响；C组实验在β=0的情况下对比MF和LSMF，验证Logistic非线性映射的有效性；D组实验测试在β=0时参数d对LSMF算法性能的影响. 由于每次得到的RMSE都已是大量数据的平均，所以每组实验只重复10次，取10次平均值作为最终实验结果.

A组实验在Epinions数据集合上随机选取x%(x=20，50，80)的数据作为训练集合，其余作为测试集合. 在不同的特征空间维度d={5，10，20，50}的情况下，对比了MF、Social MF和LSMF算法的预测准确性. MF算法中正则化系数λU=λV=0.02，学习率lr=0.005[12]；Social MF中算法中正则化系数λU=λV=0.1，社会化影响因子β=0.05，学习率lr=0.005[19]；LSMF分别选择n0=0和n0=1，其余参数为：λU=λV=0.1，λP=λQ=0.02，β=0.05，lr=0.005.

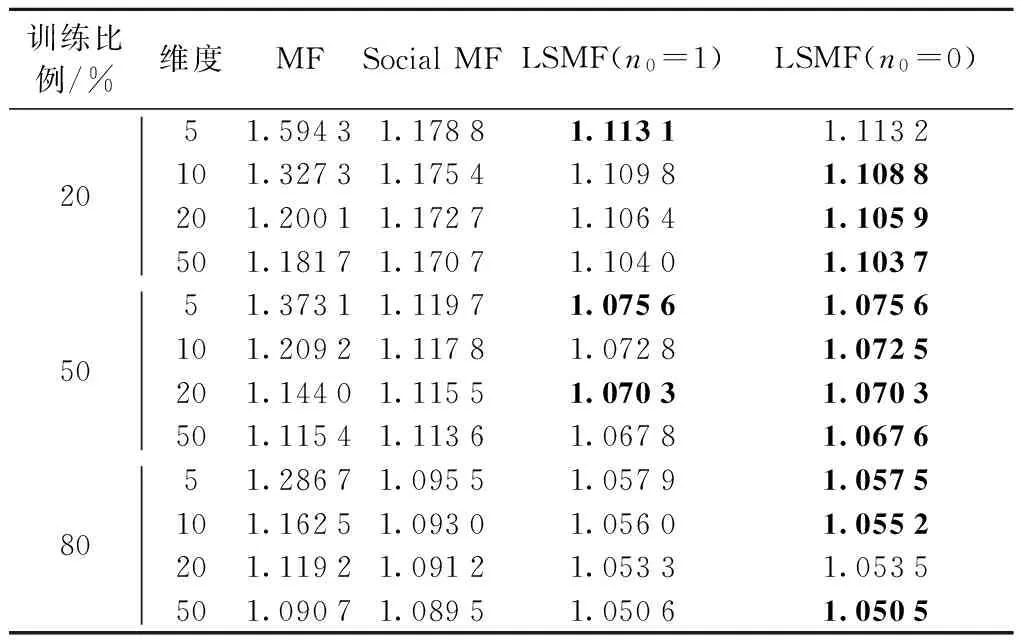
实验结果如表1所示，最小预测误差的结果用黑体标注. 在不同训练比例、不同特征维度情况下，LSMF总能取得最准确的预测结果. 在训练比例为50%、特征维度为20的情况下，LSMF的预测误差RMSE比MF减小约6%，比Social MF减小约4%. 而且，训练比例x%越低、特征维度d越小，LSMF算法的优势越明显，这说明利用社会关系能够明显缓解数据稀疏性问题，LSMF算法比Social MF算法提取潜在特征的能力更强. 随着训练集合密度和特征维度的增大，LSMF预测误差逐渐降低.

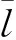
表1 LSMF与Social MF、MF在Epinions上RMSE的对比

Tab.1 Comparison of LSMF， Social MF， and MF on Epinions

训练比例/%维度MFSocialMFLSMF(n0=1)LSMF(n0=0)20508051.59431.17881.11311.1132101.32731.17541.10981.1088201.20011.17271.10641.1059501.18171.17071.10401.103751.37311.11971.07561.0756101.20921.11781.07281.0725201.14401.11551.07031.0703501.11541.11361.06781.067651.28671.09551.05791.0575101.16251.09301.05601.0552201.11921.09121.05331.0535501.09071.08951.05061.0505

B组分别从Epinions数据集中随机选取20%和80%为训练集合，其余作为测试集合. 测试了社会化影响因子β的取值对LSMF算法性能的影响，实验中LSMF的特征维度为5. 实验结果如图2所示，可以看出随着β的逐渐增大，社会关系的影响力逐渐增大，LSMF的预测误差先变小后变大，在β=0.1左右时LSMF算法能够取得较好的性能.

C组实验在MovieLens和Netflix数据集合上选取不同比例的训练集合，对比了LSMF和MF的预测准确性. MF算法的参数为：λU=λV=0.02，lr=0.005，d=20；LSMF的参数为n0=0，d=20，λU=λV=0.02，λP=λQ=0.02，β=0，lr=0.005.

如图3、图4所示，LSMF的预测误差明显低于MF，训练结合越稀疏，优势越明显. 用10%的MovieLens作为训练集合时，LSMF的预测准确性比MF高3%左右；用50%的Netflix作为训练集合时，LSMF能提高约5%预测准确性. 这说明了Logistic函数能够表征潜在因子之间的非线性关系，提高了矩阵分解模型提取潜在特征的能力.

D组实验分别在MovieLens和Netflix数据集合上测试特征维度d的取值对LSMF算法性能的影响. 分别从MovieLens和Netflix数据集合中选择10%、 50%作为训练集合，LSMF算法的其他参数同C组实验. 从图5中可以看出，在两种数据集合上LSMF算法的预测误差随着特征维度的增大而逐渐减小，体现了LSMF算法性能的稳定性.

3 结束语

本文提出了一种利用Logistic函数和社会关系信息，从非线性和社会化两个方面对矩阵分解推荐算法进行了改进. 在3组真实数据集合上的实验表明，本文提出的LSMF算法能够明显提高预测准确性，缓解数据稀疏性问题.

[1] Zhang Z K， Zhou T， Zhang Y C. Tag-aware recommender systems: a state-of-the-art survey[J]. Journal of Computer Science and Technology， 2011，26(5):767-777.

[2] LÜ Linyuan， Medo M， Yeung C H ，et al. Recommender systems[J]. Physics Reports， 2012，1(3):159-172.

[3] 刘建国，周涛，汪秉宏.个性化推荐系统的研究进展[J].自然科学进展，2009，19(1):1-15.

Liu Jianguo， Zhou Tao， Wang Binghong. Advances in personalized recommender system[J]. Progress in Natural Science, 2009，19(1):1-15. (in Chinese)

[4] Cacheda F， Carneiro V， Fernandez D， et al. Comparison of collaborative filtering algorithms: limitations of current techniques and proposals for scalable， high-performance recommender systems[J]. ACM Transactions on the Web (TWEB)， 2011,5(1):2.

[5] Bellogín A， Cantador I， Díez F， et al. An empirical comparison of social， collaborative filtering， and hybrid recommenders[J]. ACM Transactions on Intelligent Systems and Technology (TIST)， 2013， 4(1):14.

[6] Bobadilla J， Ortega F， Hernando A， et al. Recommender systems survey[M]. [S.l.]: Knowledge-Based Systems， 2013.

[7] Jamali M， Ester M. A matrix factorization technique with trust propagation for recommendation in social networks[C]∥Proceedings of the fourth ACM Conference on Recommender Systems. [S.l.]: ACM， 2010:135-142.

[8] Ma H， Zhou D， Liu C， et al. Recommender systems with social regularization[C]∥Proceedings of the Fourth ACM International Conference on Web Search and Data Mining. [S.l.]: ACM， 2011:287-296.

(责任编辑：刘芳)

A Social Matrix Factorization Recommender Algorithm Based on Logistic Function

GUO Yun-fei， FANG Yao-ning， HU Hong-chao

(National Digital Switching System Engineering and Technological R&D Center， Zhengzhou， Henan 450002， China)

The ongoing exponential growth of the Internet brings an information overload, which greatly increases the necessity of effective recommender systems for information filtering. However, collaborative filtering, which is recognized as the most successful technique in designing recommender systems, still encounters the data sparsity problem. Social relations have been found to be effective to improve the prediction accuracy of recommender systems. In order to handle the data sparsity problem, this paper proposed a new social matrix factorization recommender algorithm by leveraging the Logistic function. Experimental results on three real-world datasets illustrate that the proposed method provides more accurate recommendation results, especially under sparse conditions.

recommender system; collaborative filtering; matrix factorization; social links; Logistic function

2013-09-02

国家“九七三”计划项目(2012CB315901);国家“八六三”计划项目(2011AA01A103);国家自然科学基金资助项目(61309020)

郭云飞(1963—)，男，教授，博士生导师，

方耀宁(1987—)，男，硕士，E-mail:fyn07@163.com.

TP 393

A

1001-0645(2016)01-0070-05

10.15918/j.tbit1001-0645.2016.01.013