变式教学法在初中数学概念教学中的应用

2016-11-21王晓楠刘仁云

长春师范大学学报 2016年8期

关键词：本质属性变式图形

王晓楠，刘仁云

(长春师范大学数学学院，吉林长春 130032)

变式教学法在初中数学概念教学中的应用

王晓楠，刘仁云

(长春师范大学数学学院，吉林长春 130032)

本文针对初中数学概念的教学方法，论述了变式教学法的内涵，讨论了变式教学法对学生掌握数学概念、定义和定理，培养他们良好数学思维方法以及提高综合素质的作用，并给出了利用变式教学法的应用实例。

变式教学法；概念教学；初中数学

在初中数学教学中，数学概念教学是难点，也是热点。概念教学的方法比较多，大多数课堂采用直接给出概念，或者结合生活中的事例然后给出概念的定义，此类方法的课堂效果并不理想。如何进行概念教学是值得我们深思的课题，本文从变式的角度对这一问题进行了研究。

1 变式教学法的内涵

许多数学概念是从实际生产和生活中衍生而来，在数学概念教学中可以运用变式的方法来引入其本质属性，以促进学生对概念的理解，对于提高教学效果具有良好的作用。变式是通过变换事物的非本质特征，从不同的角度组织感性材料，在不同的形式中表现事物本质特征的过程和方法。

变式教学法，即在教学过程中引入变式方法，利用知识的非本质特征来突出其本质特征，实现教学目的的一种教学方法。它主要利用构造多种变式的方法，从不同角度向学生展示知识发生和发展的过程，并突出数学问题的结构和数学问题演变的过程，使学生在解决该数学问题时可以依据所给的变式寻求到解决同类问题的思维方法，以及创设思维障碍情境，从而在变式中达到思维训练的目的。

简单地说，如果用文字来表示，那么概念是用简洁的文字将一个复杂的事物表述出来，从而让人类通过这一事物得到认识的抽象文字。但是，无论这些文字如何表述，概念都是抽象的、不易理解的。在初中数学概念教学中，传授数学概念就更加困难了。首先，初中数学中的各个知识点和各个概念都是比较初级的，越初级的知识点解释起来难度就越大。其次，初中学生是一群特殊群体，他们的年龄正处于青少年阶段，他们对新鲜事物接受得比较好、比较快，对枯燥的介绍性的文字不感兴趣。因此，要想在这个群体中讲授枯燥的概念，教师首选变式教学法。变式教学法，可以有效地针对不同学生进行不同的训练，使基础层次不同的学生都有所收获，有利于集中他们的注意力，使学生对学习产生兴趣，发散思维，扩展视野，有效地避免了学生的厌学情绪，达到事半功倍的效果。

在数学概念教学中应用变式教学法，不仅能够让学生多角度地理解和巩固概念，还能培养学生的观察、分析以及概括的能力，开发他们的智力，培养其创新意识。

2 变式教学法在初中数学概念教学中的作用

在初中数学教学过程中，教育者需要应用行之有效的教学手段，将抽象的概念传授给学生。应用变式教学方法，使学生在不同情境中感受同一个数学知识，将枯燥的数学概念转化成学生熟知的知识，让学生在不经意间接触并接受新概念，激发他们学习数学的积极性。

2.1 变式教学有利于学生更好地掌握数学概念、公式及定理

在初中数学的概念教学中引入变式教学方法，一方面，可以使学生在观察数学公式的变化、数学定理的演算以及概念的演示的同时，清楚地认识到数学元素之间的关系，便于他们在以后的学习中自主地进行探索，找到每一个公式、定律之间的联系，培养他们的概括能力；另一方面，初中学生正处于一个特殊的过渡阶段，他们入学前所处的环境和所受的教育都不相同，其基本素养也是参差不齐，变式教学具有的针对性和概括性可以补充学生在入学前的知识缺欠，回顾上一阶段的数学知识点，起到平衡数学水平、全面提高班级数学水平的作用。

2.2 变式教学法有利于学生养成良好的思维方法

将变式教学应用在初中数学概念教学中，有利于学生养成良好的思维方法。变式教学是丰富多样的，它能让一个数学公式有多种转换，从而映射出更多的数学公式和定理。这就相当于一个圆形的辐射教学模式，这种教学模式应用到数学概念教学中，可以使学生通过学习一个知识点辐射出多个知识点，增加了教学效率，降低了学习压力，同时增加了数学学习的趣味，这样耐人寻味的学习感受，可以吸引学生去思考更多知识点之间的联系，培养学生在学习中不拘泥于某一方面，便于学生思考这些知识点背后的根源，开发他们的创造力。

2.3 变式教学有利于提高学生的综合素养

变式教学可以从图形、公式、定理等几个方面进行变式和演化，变式的角度丰富多样，这样的教学方法为学生营造一个非常广袤的想象空间，学生在这种教学模式下能够很自然地形成逆向型思维，从不同角度思考问题，在思考中学习，在学习中思考，通过教师的变式的引导，多方面、多角度地去接受新知识、新概念，理解新概念的实质，轻松愉悦地掌握抽象难懂的数学概念。

3 变式教学法在初中数学概念教学中的应用举例

变式教学法在具体的应用中会分支出许多类别，本文举出其中两种变式方法用以说明变式教学法在数学概念教学中的重要性。

3.1 类比归纳变式教学法

数学概念具有一定的抽象性，并且有很强的概括性，学生很难在书面上完全理解数学概念的实质和内涵，甚至有些概念通过教师的讲解，学生理解得也不是十分透彻，对于这样的问题，教师可以通过应用类比变式，来帮助学生理解数学知识的含义。例如，讲解一元二次方程的概念，教师通过创设情境，分别提出多个问题，让学生列方程，引发学生思考，提高学生探究兴趣。教师在开始讲解一元二次方程的基本概念之前，设置了一系列情境，让学生自己根据情境列方程。

情境1 如图1所示，点C在线段AB上，如果点C是AB的黄金分割点，那么AC/AB=CB/AC。

图1 情境1图示

假设AB=1，AC=x，则有BC=1-x，根据已知有x/1=(1-x)/x，即x2+x-1=0。

情境2 已知一个长方形的面积是40cm2，现将它的一个边长增长5cm，另一个边长增长3cm，此时正好形成一个新的四边形——正方形，那么这个正方形的边长是多少？

假设新正方形的边长是x，则长方形的边长分别是(x-5)和(x-3)，则根据已知有(x-5)(x-3)=40，即x2-3x+30=0。

情境3 学校要组织年度篮球赛，参赛队每两个队要比赛一场，最终得出获胜队，根据场地和时间等条件，比赛将进行5天，每天安排3场比赛，则一共有多少个队参赛？

假设一共有x个队参赛，则全部比赛共有0.5x(x-1)场，根据已知有0.5x(x-1)=3×5，即x2-x+30=0。

教师引导学生观察以上方程的共同点，并归纳总结出一元二次方程的本质特征，从而引出一元二次方程的概念。学生通过类比归纳出新知识的概念，再经过练习变式习题巩固和辨析新知识的概念，对新概念彻底地理解和吸收，并与已有知识进行整合。以上案例展现了类比归纳变式的应用特点，通过对三个问题情境的分析，可以总结出一元二次方程的概念，再通过变式习题中的非概念变式和概念变式，让学生理解辨析了一元二次方程的概念，也掌握了其本质属性。

3.2 图形变式教学法

在初中几何课程的学习过程中，学生习惯于标准图形，容易由习惯形成思维定式，自以为掌握了新概念的本质属性，但在需要动手实践的时候，学生常常混淆新概念的本质属性与其非本质属性，将非本质属性误认为是本质属性了。基于这种情况经常发生，笔者便对概念教学进行了深入研究，发现在几何概念教学中，可利用图形的变式来突出新概念的实质，采用图形变式来变换新概念本质的表现形式，变换人们以往观察事物的角度和方法，从而突出新概念中隐含的本质要素，避免混淆本质属性，达到对新概念的准确理解。

例如，讲解同位角、内错角、同旁内角的概念，清楚这三个角与角的位置关系的概念，对于初学几何知识的学生来说是至关重要的，这些概念是学习平行线的性质和判定的前提，为以后学习三角形和平行四边形打下坚实的基础。初中数学教材中给出了一个标准的几何图形(图2)，并且按照图2给出了同位角、内错角和同旁内角的文字定义。

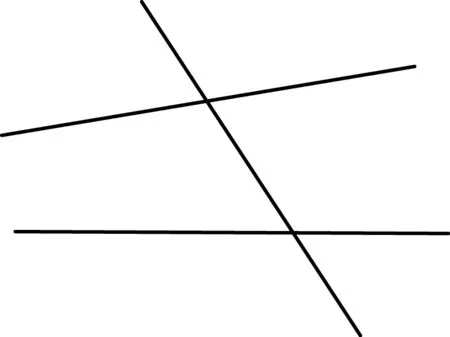
图2 初中数学教材标准几何图形示例

教师在教学过程中，可以不拘泥于教材中的一种图形进行讲解，适当采用图形变式，在变化新概念的非本质属性的同时突出其本质属性，如给出如图3、图4、图5所示图形，让学生从多个角度理解新概念。

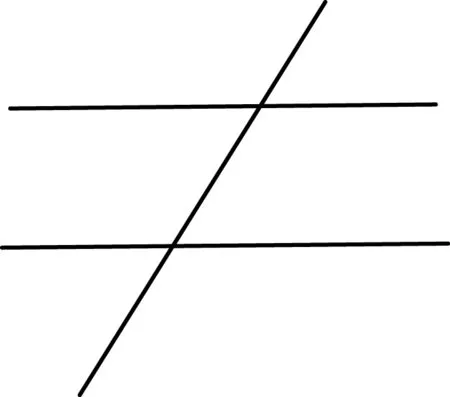
图3 图例1

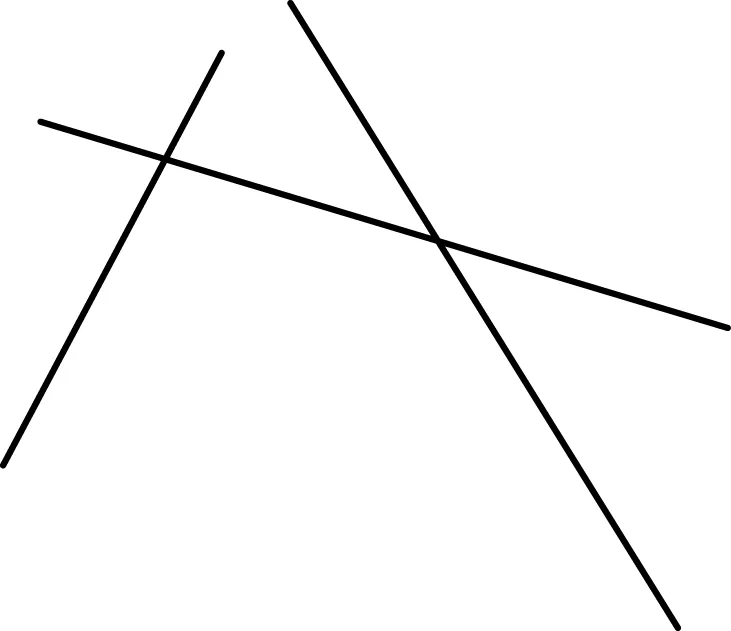
图4 图例2

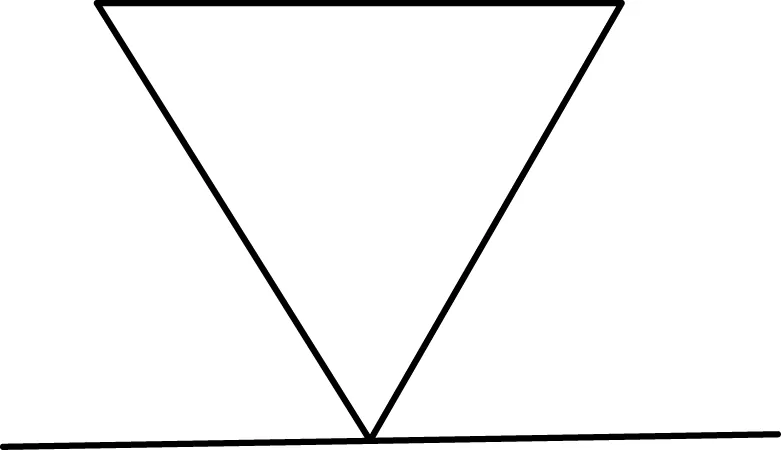
图5 图例3

在学生理解新概念的本质属性后，教师可根据学生的理解程度从新概念的内涵和外延分别作变式练习，使学生通过对这些变式的练习，达到对新概念本质的进一步深化理解的目的。以上案例可以凸显几何概念教学的特点。教师在描述几何概念时可以用三种语言对其描述，即文字语言、符号语言和图形语言。学生在进行几何学习时，对图形语言是比较敏感且易懂的，教师要利用学生的这个特征，从图形入手，对图形进行变式，使学生从多角度理解几何概念，深层次理解概念的实质。这样，概念教学可以达到事半功倍的效果。

4 结语

时代在进步，人们的思想在改变，科学设计数学概念的教学显得尤为重要，将变式教学方法引入到数学概念的教学中是一种科学有效的教学方法。教师运用变式教学，不仅能使学生学到知识，而且时间久了学生从“学会”逐渐转变到了“会学”，提升了学习能力。在变式概念教学的课堂上，学生掌握了学习方法，就能够有效地与教师进行互动，享受变式给他们带来的欢乐，轻松愉悦地进行数学学习，使之前枯燥乏味的数学课堂变得生机勃勃，充满活力。

[1]曹达峰.变式教学法在概念教学中的应用及思考[J].数学教学与研究,2014(7):66-68.

[2]王萍萍.数学概念课的变式教学[J].内蒙古电大学刊,2013(2):111-112.

[3]祖惠泊.变式在初中数学教学中的应用研究[D].北京:首都师范大学,2004.

[4]涂荣豹,宁连华.中学数学经典教学方法[M].福州:福建教育出版社,2013.

[5]涂荣豹.数学教学认识论[M].南京:南京师范大学出版社,2006.

[6]曹一鸣.数学教学模式导论[M].北京:中国文联出版社,2002.

[7]张春莉,王小明.数学学习与教学设计(中学卷)[M].上海:上海教育出版社,2014.

[8]施良方.学习论[M].北京:人民教育出版社,2001.

[9]孔凡哲,孟祥静.新课程理念下的创新教学设计(初中数学)[M].长春:东北师范大学出版社,2005.