有机构成提高导致利润率下降的条件及其背后的矛盾关系

骆　桢

（四川大学经济学院成都610065）

有机构成提高导致利润率下降的条件及其背后的矛盾关系

骆桢

（四川大学经济学院成都610065）

在弗雷等人构建的单部门实物量模型基础上引入劳动价值论，用以分析技术构成提高导致价值构成提高的条件。研究发现，技术构成提高能否表现为价值构成提高，取决于技术进步的类型。而技术进步的类型背后所体现的是生产力能否得到持续发展。分析得出，有机构成提高导致利润率下降是资本主义生产关系不适应生产力发展需要的表现。也就是说，资本主义生产的目的和手段的矛盾应从属于“生产力-生产关系”的矛盾运动。

有机构成；利润率下降；资本主义矛盾

马克思的平均利润率下降规律理论是学界理解其理论体系中争议较大的部分。对利润率下降理论的质疑主要集中于新技术导致劳动生产率提高从而在有机构成提高的同时提高了剩余价值率。而剩余价值率的提高可能会超过有机构成的提高，从而导致利润率不下降甚至反而上升。［1］［2］［3］［4］而“置盐定理”更是在“李嘉图-斯拉法”均衡价格体系下证明了若实际工资不变，在原有价格体系下节省单位成本的新技术必然使得利润率上升。［5］从而，他认为利润率下降的原因不是技术进步，而是实际工资的变动。且不论“置盐定理”假设条件存在的问题，［6］本文认为该定理和其他的基于剩余价值率提高而否定利润率下降理论的观点并未对马克思的利润率下降理论构成真正的挑战。

虽然马克思的平均利润率下降规律是在假定剩余价值率不变的前提下得出的，但是马克思紧接着就在后面说明了“阻碍利润率下降的因素”，其中大部分都是通过提高剩余价值率来发挥作用的。而剩余价值率受到实际工资和单位消费品价值量的共同影响。实际工资和单位消费品价值量之间也并不总是独立运动的，随着生产力的进步和消费品单位价值量的下降，实际工资也有提升的长期趋势。然而，不管这一运动的内部结构怎样，其在总体上体现为新增价值量在劳资之间的分配关系。而分配关系，体现的是劳资之间的权力对比，在资本积累和景气波动过程中，剩余价值率所体现的分配关系也会相应波动。从而，马克思在得出利润率下降趋势这一结论的时候，显然是将体现收入分配关系的剩余价值率的影响抽象掉了，这意味着利润率下降作为一个长期趋势的理论将资本积累的短期动态抽象掉了。

从这个意义上看，剩余价值率变动对利润率下降趋势的影响，并不是马克思所忽略的因素，而是马克思在更高的抽象层次分析利润率长期趋势时所抽象掉的因素。但是，如果技术构成提高必然导致有机构成的提高，则利润率下降似乎变成了一个技术进步的必然结果。一方面，这难以解释历史上技术进步带来的持续资本积累和经济增长。另一方面，生产力（技术）进步导致利润率下降从而激化资本主义矛盾，这貌似印证了资本主义为自身灭亡准备条件的辩证逻辑，但是如果资本主义适应并促进生产力发展，其内在矛盾就不应该在此时激化甚至引致消亡。从生产力和生产关系的辩证逻辑出发，资本主义内在矛盾激化应该是资本主义不再适应生产力发展的表现。

本文认为，解决上述问题的关键在于技术构成的提高导致价值构成提高的条件上。马克思在分析阻碍利润率下降的因素中也提到了生产资料变得便宜这一因素，这意味着技术构成提高并不在逻辑上等同于价值构成提高。因此，即使在分析利润率长期趋势的时候抽象掉资本积累的短期动态和收入分配变化，技术进步带来的生产率的提高仍可以发挥抵消利润率下降的作用。然而现有的文献对有机构成提高的讨论主要集中于经验数据方面。［7］［8］38～150［9］本文的分析将说明，技术变动并不必然意味着生产力的进步，有机构成提高恰恰是生产力发展迟缓的表现。为了对此进行说明，我们首先要引入一个关于技术变动的模型，以区分技术变动的两种类型。

一、技术变动的机制和两种技术变动类型

弗雷（Foley）等人试图通过一个单部门实物量模型绕开劳动价值论来分析技术变化的内在结构。［10］实物量模型通常面临加总难题，但是单部门模型中，投入和产出都是同一种产品，所以回避了价值理论的选择。但也正因为如此，我们发现该模型在厘清技术变动中各参数的影响时，并没有真正反映出马克思关于资本主义矛盾和技术变动之间的关系。

该模型基于一个固定系数生产函数：Q=min［eL，ρK］，其中Q为总产量，L为所投入劳动，K为所投入的资本数量，e=Q/L为劳动生产率，ρ=Q/K为资本产出率。总产出可分为实物量表示的总工资W和总利润Z，于是有Q=W+Z。等式左右两边除以总劳动，写成人均的形式有e=w+z，其中w是人均工资，z是人均利润。令实物量利润率r=Z/K，人均资本量k=K/L=e/ρ，可得：

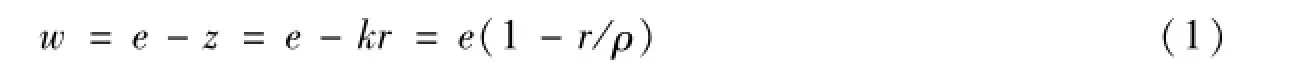
于是，工资和实物量利润率之间存在着负相关的线性关系，其斜率的绝对值就是实物量意义上的人均资本，如下图（1）所示：

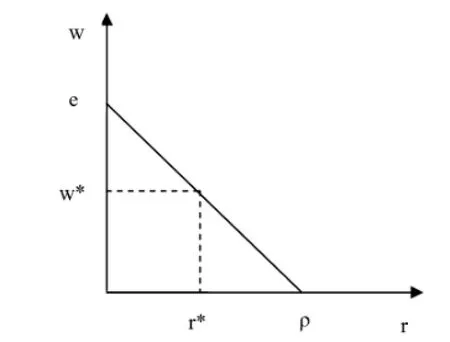
图1

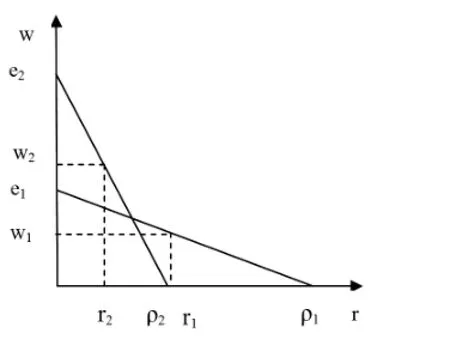
图2

由（2）可见，在剩余价值率或者说劳资分配比例不变的前提下，随着劳动生产率的提高，实际工资必然上升。弗雷认为工资的上涨正是技术变化的原因，因为工资提高之后新技术的利润率相对更高。整个机制如图（2）所示。

图（2）中有两种技术，（e2，ρ2）相对于（e1，ρ1）劳动生产率更高而资本产出率更低，这意味着技术2的技术构成更高。当工资上升到一定程度，新技术利润率更高，从而资本逐利还会导致技术变迁。弗雷等人将劳动生产率提高，同时资本产出率下降的新技术称为“马克思式”的技术变革。从图2中易见，该新技术满足技术构成（人均资本量）提高，同时（实物量）利润率下降。

以上机制不失为对技术变迁微观机制分析的有益尝试，但是如果将该机制作为理解马克思利润率下降趋势理论背后的逻辑过程就未免有失偏颇了。

首先，马克思对技术进步的假设并没有涉及到资本产出率的变动。马克思所提出的技术构成提高并不等同于劳动生产率提高的同时产出-资本率下降。根据定义，劳动生产率的增长只要高于资本产出率的提高，都意味着技术构成提高。其次，他们认为（实物量）利润率的变动由技术进步的特定模式决定，从而忽略了资本主义制度对技术进步的影响，以及利润率变动所体现的资本主义的矛盾。因此，该模型将利润率下降趋势理解为特定技术进步类型的结果，而不是资本主义内在矛盾的体现。最后，在总量（单部门）模型中，实物量利润率的分子和分母同时乘以单位商品价值量就得到了价值量利润率，因此两者的变动趋势应该是一致的。按照该模型的定义，实物量利润率下降的条件仅仅依赖于资本产出率下降，而不是技术构成的提高，更不论有机构成了。我们对此做简单证明，根据（1）式，我们有r=（1-w/e）ρ，再根据（2）式，得：

由（3）式可知，给定剩余价值率不变，利润率的变动仅仅取决于资本产出率。因此，脱离劳动价值论和资本主义内在矛盾的分析，是无法理解利润率下降趋势真正的理论内涵的。为了说明以上问题，我们必须考虑两种技术进步的模式及其对应的函数表达。线性生产技术由劳动生产率（e）和资本产出率（ρ）两个参数决定，按其变化的组合有四种。首先，排除掉e和ρ都减小的变化，该技术会导致利润率在任何工资水平下都下降。其次，考虑到随着经济增长劳动力需求会持续上升，同时经济社会发展必然提高劳动力再生产所需的实际工资，那么e下降且ρ上升（和图（2）相反）的新技术即使在当前工资水平下利润率更高，也会随着实际工资上涨而被淘汰。因此，我们主要分析e上升、ρ下降，以及两者同时上升这两种技术变化及其背后的矛盾因素。

如果我们将该两种技术进步下的单位产出要素投入关系对应起来，就可以得到下图。图（3）描述的是e上升同时ρ下降的技术变化。

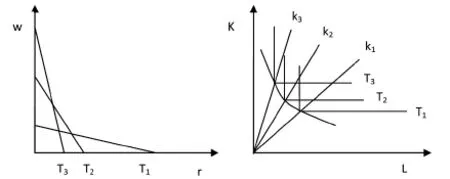
图3

从图（3）可以看到，实际工资上升可以使得技术从T1逐步变化到T3，这个过程中劳动生产率e提高，而资本产出率下降。从右边的的单位产出等产量曲线的变化可以看出，随着技术变化，技术构成（即人均资本数量k）不断提高。因为企业数量众多，当一部分企业采用新技术的时候，另一部分企业还在沿用老技术。从而，行业总体的单位产出要素组合就会沿着不同技术下要素投入组合的“凸组合”向上移动，形成一条近似的凸向原点的“等产量曲线”，该现象也被称为“化石生产函数（fossil production function）”①。［11］该曲线上方的部分，就是能够生产出单位产出及其以上产量的“要素投入集”。

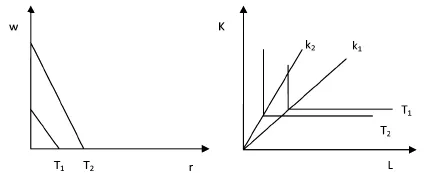
图4

从图（4）可见，我们令该类型的技术变化仍然保持了技术构成的提高，但是技术变动并不依赖于实际工资水平上升这一条件。从单位产出的要素投入情况来看，该型技术进步使得要素投入集向左下方“扩展”。由此，从要素投入的角度看，技术进步的两种类型可以总结为下图（5）中的两个方向：

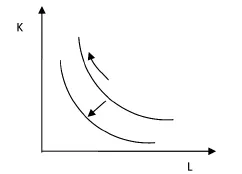
图5

我们用函数Q=F（A，K，L）来描述投入-产出关系的变化。当A不变时，意味着技术变动沿着“化石等产量曲线”变动；而系数A的增大描述的是技术进步带来的当前要素投入集的“扩展”，以至于原有要素投入下产出水平更高，也就是∂F/∂A≥0。同时，因为“化石等产量曲线”是线性技术要素投入的凸组合，所以，一方面，产出是要素的非减函数②，即∂F/∂K≥0，∂F/∂L≥0；另一方面，每一个要素投入组合代表一种线性生产技术，这意味着函数F（A，K，L）关于K和L是一次齐次的，即F（A，αK，αL）=αF（A，K，L）。

基于以上设定，我们可以得到技术变动中劳动生产率e（人均产出）和技术构成k（人均资本量）之间的关系：

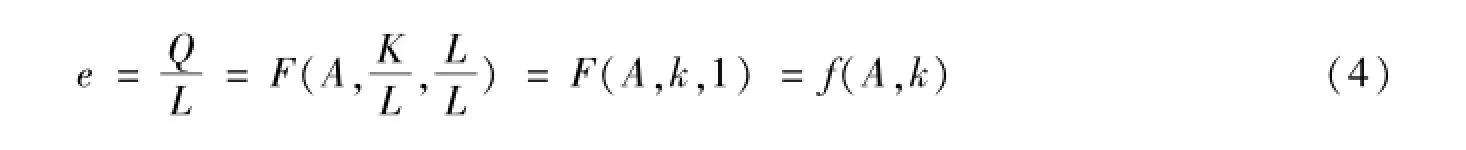
由（4）可知，沿着“化石等产量曲线”进行的技术变化对应的是A不变，依靠k的积累提高劳动生产率e，而A的增大则对应要素投入集的扩展。按照马克思的观点，从历史经验来看，技术进步在现象上体现为采用了更多更新的机器和自动化生产。于是，我们进一步假设A的增长源于技术构成的提高，即A =A（k），且dA（k）/dk≥0。当然，并不是所有技术构成的提高都能带来A的变大和要素投入集的扩展。

二、有机构成提高条件及其与生产力进步的关系

弗雷等人的模型已经对实物量关系的变动进行了说明，为了弥补其模型缺陷，我们考察该模型的价值量变量的关系。考虑到固定资本折旧的问题③，本期总产品价值量为本期投入的总劳动和固定资本折旧的价值之和。因此，单位产品价值量为：

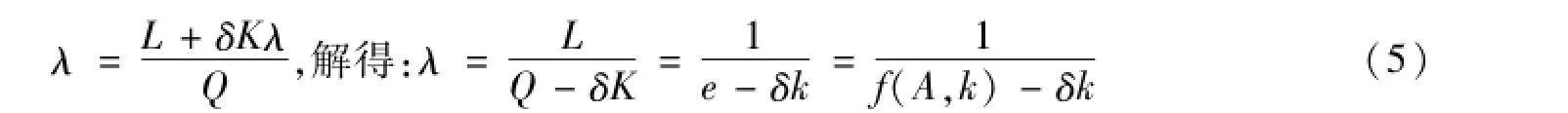
其中，δ为折旧率。因为当期活劳动可分为必要劳动和剩余劳动，所以L=m+v，有机（价值）构成θ可写作：

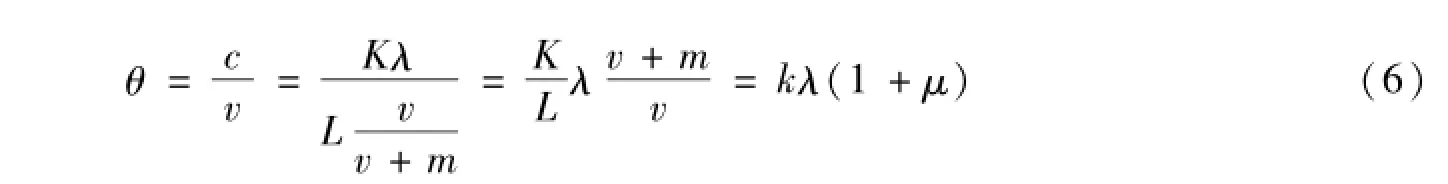
其中，μ为剩余价值率。将单位产品价值量代入上式，得：

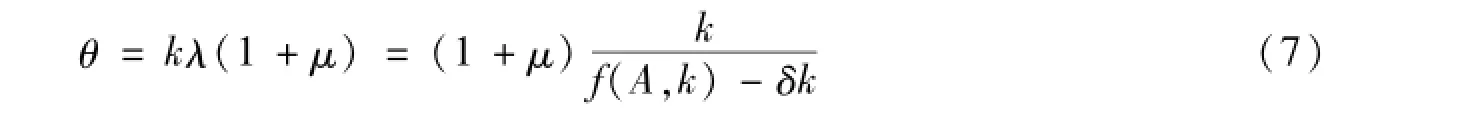
基于以上设定，我们可以得出以下两个命题：

命题1：若没有要素投入集的扩展（即A不变），则技术构成的提高一定会导致价值构成提高，从而体现为有机构成的提高。

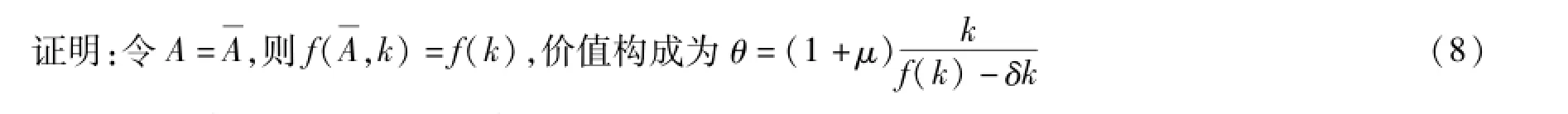
于是，用价值构成对技术构成求导，得

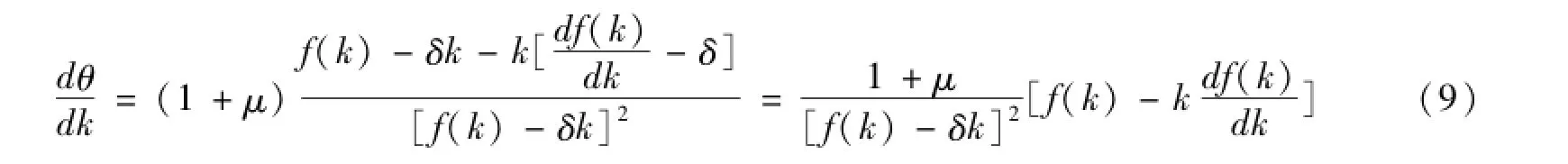
命题2：若技术构成提高带来要素投入集的扩展，即A=A（k），且dA/dk＞0，则资本的平均产出持续增长意味着技术构成提高不会带来价值构成的提高。从而，技术构成提高不会体现为有机构成提高，也不会导致利润率下降。

证明：若技术构成提高不带来价值构成的提高，这意味着：

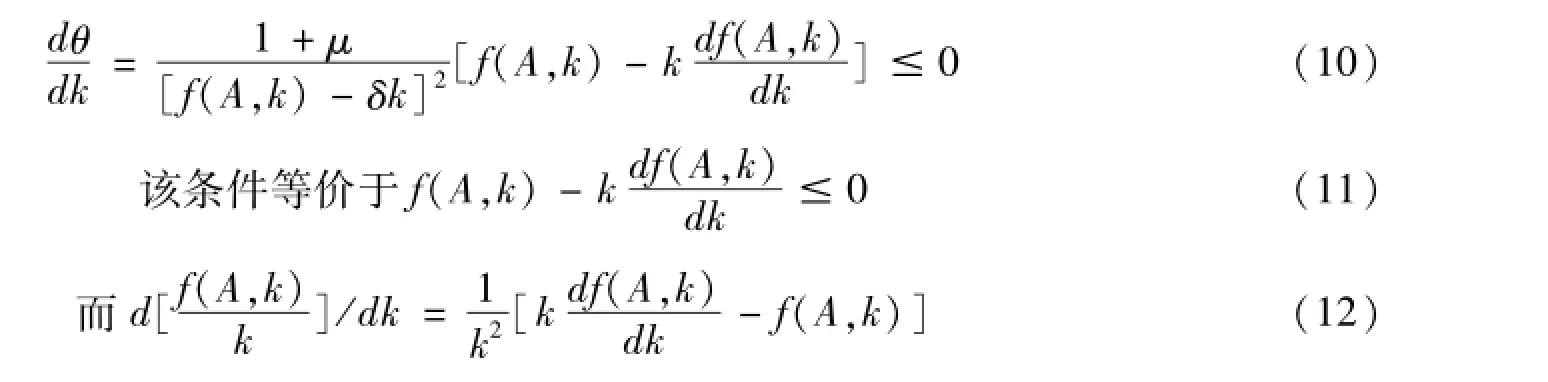
以上结论，也恰恰和弗雷等人的实物量利润率变动条件保持了一致。然而，这似乎意味着，有机构成提高导致利润率下降能否发生取决于技术进步的类型。这又回到了本文对前面实物量模型的批评上，也就是利用技术因素来解释经济规律，而不是资本主义内在矛盾。对此，我们基于劳动价值论可以发现以上两种技术进步类型并不仅仅是技术参数的不同。下文将证明，在要素投入集无法有效扩展的技术进步类型下，生产力的发展是不可持续的。这意味着，两种技术进步类型所体现的生产力与生产关系的关系是不同的。

我们用人均净产出（扣除折旧之后的人均产出）来代表生产力的发展。于是，假设劳动力总量不变，则人均有效产出为

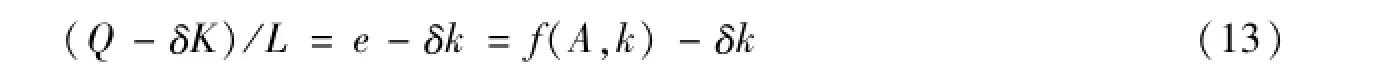
那么，劳动力总量不变时，技术构成提高能否带来人均净产出的持续增长，取决于下式是否大于零：

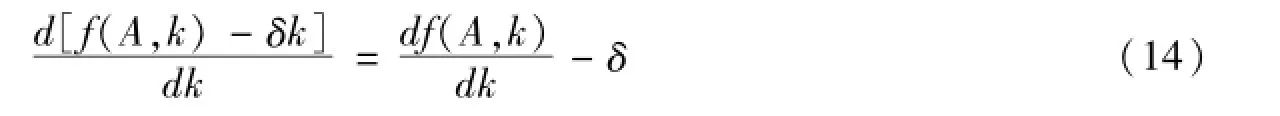
由此可见，人均净产出的持续增长与否取决于技术变动中技术构成的提高能否带来劳动生产率的足够多的提高，至少高过折旧率。如果我们将此作为生产力进步与否的标准，那么可以提出以下命题：

命题3：带来要素投入集扩展且资本平均产出持续提高的技术变化（即技术构成提高不带来价值构成提高）能保证生产力的持续进步，而要素投入集不扩展的技术变动则难以带来持续的生产力的持续进步。

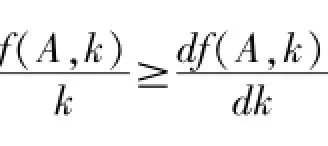
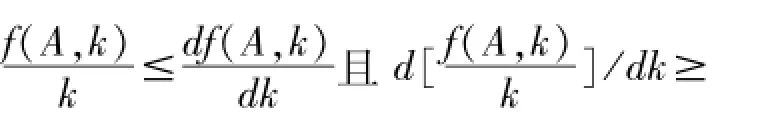
三、有机构成提高的条件与资本主义内在矛盾

以上分析表明，如果技术变动中，技术构成提高并不表现为价值构成的提高，也就是有机构成提高导致利润率下降规律不发挥作用的时候，恰恰意味着人均产出因为技术构成的提高持续增长，即生产力的持续发展。如果技术变动中，技术构成提高体现为价值构成的提高，而且剩余价值率的变动无法抵消该趋势时，则利润率下降。此时即使还能持续积累，随着积累的进行和技术构成提高，劳动生产率的提高会越来越慢，最终甚至在扣除折旧之后所剩无几。这意味着生产力进步的迟缓。因此，我们可以看到技术构成能否体现为价值构成的提高，取决于技术变动本身是否能带来生产力的持续发展。

由此可见，有机构成提高导致利润率下降规律能否发挥作用，取决于生产关系是否适应并推动生产力持续发展。也就是说，并不是生产力越进步，利润率反而越低，而是生产力持续进步的时候利润率下降规律会得到抑制，生产力发展受阻时，则利润率下降作为现实的规律会进一步激化矛盾。

更进一步，我们从图（c）、（d）可以看到，虽然两种技术变动都是利润导向的行为，但正如图（c）所示，导致价值构成上升的技术变动的前提是实际工资的上涨。这背后体现的恰恰是资本主义生产方式下的劳资矛盾。在马克思的理论中，价值构成的提高在资本积累和景气循环中确实发挥着不可忽略的作用。随着资本积累的进行，失业率持续下降会带来工资水平的上升。为了抑制工资上涨，资本家会通过机器替代劳动，生产“相对过剩人口”以相对减少资本积累对劳动力的需要。然而，若技术构成提高无法带来价值构成的提高，则无法减少资本积累中预付可变资本所占比重，从而无法相对减少资本积累对劳动力的需求，也就无法阻碍工资水平的提高。这一过程虽然伴随着生产力的巨大进步和剩余生产效率的持续提高，但是无利于资本权威的维持。从而，当工资上涨到一定程度，就会挤压利润，导致资本积累停滞甚至经济危机。也就是通过资本存量的毁灭来减少生产和资本积累对劳动力的需求。这就是马克思所说的“一种情况是，劳动力价格继续提高，因为它的提高不会妨碍积累的进展；……另一种情况是，积累由于劳动价格的提高而削弱，因为利润的刺激变得迟钝了。积累减少了。但是随着积累的减少，使积累减少的原因，即资本和可供剥削的劳动力之间的不平衡，也就消失了。所以，资本主义生产过程的机制会自行排除它暂时造成的障碍。劳动价格重新降到合适资本增值需要的水平，而不管这个水平现在是低于、高于还是等于工资提高前的正常水平。”［12］

这里，我们可以看到，在资本主义生产方式下，技术构成提高不引起价值构成提高就难以通过制造相对过剩人口来强化资本权力。而且，即使存在生产力的巨大进步，也难以维持在资本强权的生产方式下的持续资本积累。而通过技术构成提高引起价值构成提高，从而相对减少资本积累对劳动力的需求，则可强化资本对劳动的权威，然而这会造成利润率下降。因此，从这个意义上看，资本主义生产方式也是充满矛盾的。

注 释

①弗雷等人将这样的曲线称为“化石生产函数（fossil production function）”，也就是说这只是技术变动的历史记录，而不是当前技术的体现。我们这里也沿用了这一说法。

②线性生产技术条件下，单一要素增加并不能带来产出的增加。但是一旦有两个线性技术做凸组合，则要素增加意味着该要素投入组合可以是两种技术下，更高产量的要素投入的凸组合，从而单一要素增加是可以带来产量的上升的。

③该模型并没有考虑折旧，但是即使将折旧加进模型，其分析仍然成立。因为模型中最重要的工资和（物量）利润率的负相关关系依旧成立，而且依旧是线性关系。

［1］斯威齐.资本主义发展论［M］.北京：商务印书馆，1997：118-224.

［2］霍华德.马克思主义经济学史［M］.北京：中央编译出版社，2003：130-144.

［3］Wolff E N.The Rate of Surplus Value，the Organic Composition，and the General Rate of Profit in the U.S.Economy，1947 -67.［J］.American Economic Review，1979，69（3）：329-41.

［4］沙洛姆·格罗，泽夫·B·奥泽奇，张开译.马克思利润率下降理论中的技术进步和价值：一个注解［J］.北京：政治经济学评论，2012（4）：186-207.

［5］Okishio，N.Technical changes and the rate of profit.［J］.Kobe University Economic Review，1961，7：85-99.

［6］骆桢.对“置盐定理”的批判性考察［J］.北京：经济学动态，2010（6）：120-124.

［7］Moseley F.The Rate of Surplus Value，the Organic Composition，and the General Rate of Profit in the U.S.Economy，1947 -67：A Critique and Update of Wolff's Estimates［J］.American Economic Review，1988，78（1）：298-303.

［8］高峰.资本积累理论与现代资本主义［M］.天津：南开大学出版社，1991：38-150.

［9］Cockshott W P，Cottrell A.A note on the organic composition of capital and profit rates［J］.Cambridge Journal of Economics，2003，27（5）：749-754.

［10］Foley DK，Michl TR.Growth and distribution［M］.Harvard University Press，1999：11-67.

［11］李海明.一个古典-马克思经济增长模型的中国经验［J］.北京：经济研究，2014（11）：159-169.

［12］马克思.资本论：第1卷［M］.北京：人民出版社，2004：715-716.

责任编辑：魏旭

F03

A

1005-2674（2016）08-012-07

2016-06-12

国家社会科学基金青年项目（14CJL038）

骆桢（1983-），男，重庆万州人，经济学博士，四川大学经济学院讲师，主要从事马克思主义经济学研究。