基于相位补偿法和粒子群算法的PSS4B参数优化方法*

沈　鑫，马红升，李仕林，王　昕，刘清蝉

（云南电网有限责任公司电力科学研究院，昆明650217）

基于相位补偿法和粒子群算法的PSS4B参数优化方法*

沈鑫*，马红升，李仕林，王昕，刘清蝉

（云南电网有限责任公司电力科学研究院，昆明650217）

随着电网规模越来越大，电力系统低频振荡问题日益突出。电力系统稳定器是解决低频振荡的有效措施之一，针对目前使用的PSS存在一些不足，对宽频段的电力系统稳定器进行了研究，并采用基于相位补偿法和粒子群优化算法对宽频段电力系统稳定器的模型参数进行优化，通过RTDS仿真和现场实测，说明优化后的PSS4B能够满足不同宽频段的要求，有效抑制低频振荡。

电力系统稳定器；相位补偿法；粒子群算法；宽频段；参数优化

随着高增益快速励磁系统的广泛应用和大系统之间的弱互联，系统对振荡的阻尼作用将会减弱，从而在小扰动作用下容易引发低频振荡，限制了互联系统间的功率传输。励磁系统的附加电力系统稳定器PSS（Power System Stabilizer）控制可以有效抑制低频振荡的发生，改善电力系统运行的安全性和经济性［1］。全国联网工程的研究表明，我国区域电网之间存在0.1 Hz～0.3 Hz的低频振荡模式，在没有配置PSS的情况下，成为负阻尼振荡模式。

目前，PSS仍然是抑制电力系统低频振荡、提高系统稳定性的首选措施，但是新的电网发展形势对于现有的PSS提出了新的要求：需要有更宽的工作频域。现在我国广泛采用的PSS2A/B以合成加速功率作为输入信号，有效克服了“无功反调”现象，但其为单分支结构，增益特性随频率单调递增，高频段和低频段增益差距显著往往难以兼顾，特别是PSS2A/B的两级隔直环节导致0.2 Hz附近的低频段总提供较大的相位领先，限制了稳定器可提供的正阻尼，有时甚至提供负阻尼。

为了满足现代电力系统的需求，一种多频段电力系统稳定器PSS4B应运而生。PSS4B在2000年由加拿大魁北克电力局提出，适合加拿大电网分省管理、跨国送电的复杂的形式，目前国内只有华北电科院联合ABB在现场作了适应性检测，并无实际工程应用。PSS4B模型是在PSS2A/B模型的基础上加以改进形成，其最大特点在于将转速/功率信号分为低频、中频及高频3个频段，分别对应低频振荡范围的各频段，可在更大的频率范围内提供更好的灵活性来实现更优的抑制振荡阻尼性能。现有的对于PSS4B模型［2］及其改进模型［6-10］的理论研究已经较为成熟，但是针对相应参数整定研究并未深入，往往采用典型参数使得众多参数的灵活性并未得到充分利用。本文提出一种基于相位补偿法和粒子群优化算法的PSS4B参数优化方法，根据单机无穷大系统中机组励磁控制系统滞后特性，通过补偿实现了整个宽频段范围内补偿误差最小，并且幅频特性能够同时兼顾高低频段，最后通过RTDS进行了试验仿真验证。

1　相位补偿法优化PSS

1.1基于单机无穷大系统的无补偿频率特性计算

励磁控制系统滞后特性即无补偿频率特性，是指附加力矩对于PSS迭加点的滞后角度，是PSS参数优化的基础。目前对于无补偿频率特性的获取多通过公式计算，即利用发电机数据和发电机出口到无穷大系统的等值电抗值，通过线性化Heffron-Philips模型计算。对于远离负荷中心的发电机，可以将发电机以外的系统等值为一个单机无穷大系统，系统包含系统电抗Xs=XL+XT和无穷大母线Vs，如图1所示。

图1　单机无穷大系统

单机无穷大系统Phillips-Heffron模型的传递函数如图2所示。

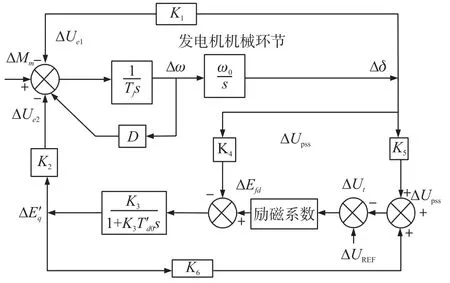
图2　单机无穷大系统线性化Phillips-Heffron模型

由图2可知，无补偿频率特性即为ΔEq′/ΔUpss的频率特性，ΔUpss为PSS输出的控制信号，无补偿频率特性的计算范围按照PSS4B补偿要求设置为0.04 Hz～4.00 Hz。

1.2相位补偿法基本原理

相位补偿法［11］是PSS参数整定的经典方法之一，具有适应范围广、鲁棒性强的优点。图2中发电机机械环节就是发电机转子运动的线性化方程，机械环节以外的部分对电磁转矩贡献记作ΔMe2。由图2可知

式中，Mdelta（s）和Mpss（s）分别为从Δδ和ΔUpss到ΔMe2的前向通道的传递函数。转矩分析就是将ΔMe2在Δω-Δδ坐标上分解为阻尼转矩（与Δω成正比）和同步转矩（与Δδ成正比），即

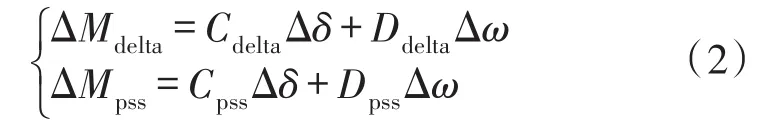
式中，Cdelta和Cpss为同步转矩系数；Ddelta和Dpss为阻尼转矩系数。若PSS的传递函数为Gpss（s），输入信号为Δω，相位补偿设计PSS就是整定PSS参数，使得在整个低频振荡范围内PSS输出的力矩向量对应Δω轴超前不大于10o、滞后不大于45o（即在-80o～-135o有补偿特性），尽可能在不影响同步转矩的情况下提供更大的阻尼转矩［2，19-20］，即

ωs为系统低频振荡角频率，即

不同运行方式下系统振荡模式不同，一般采用智能算法来寻求一组PSS参数，使其同时补偿整个频段上的励磁系统相位滞后，从而为各种运行方式都提供最大的阻尼转矩。本文将采用文献［14］介绍的PSO算法并对其进行适当改进，采用该优化算法可以在限定的参数范围内寻找目标函数的最优解。PSO算法的特点在于收敛速度较快、算法简单、容易编程实现，虽然提供全局搜索的可能，但是并不能保证搜索到全局最优点。综合考虑，为了平衡粒子群算法的全局搜索能力和改良局部能力，自适应地改变惯性权重ω，如式（5）所示。即当各微粒的目标值趋于一致或者趋于局部最优时，将使惯性权重增加；而各微粒的目标值比较分散时，将使惯性权重减小。同时对于目标函数值优于平均目标值的微粒，其对应的惯性权重因子减小，从而保护了该微粒；反之对于目标函数值差于平均目标值的微粒，其对应的惯性权重因子较大，使得该微粒向较好的搜索区域靠拢。

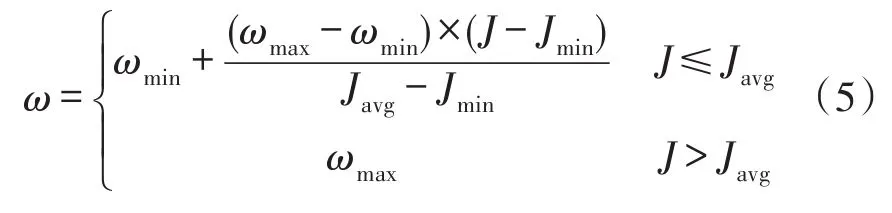
式中，ωmax，ωmin分别为惯性权重的极值，J，Javg，Jmin分别为微粒目标函数，目标函数平均值以及最小值。

2　PSS4B参数优化

2.1PSS4B模型及参数分析

PSS4B的数学模型如图3所示，以发电机转子转速/有功功率为输入信号，通过信号采集传感器作用，将输入信号分离为低频、中频和高频3个频段。每个频段都由正、负两个分支组成，每个分支又由增益模块、中心滤波环节和两个标准的超前滞后模块组成。从结构上看，相对于之前出现的稳定器，PSS4B主要具有以下两个优点［2］：

（1）双偷入之前传统的PSS2A，仅采用了单一输入信号，可能会出现较严重的“反调”现象。而PSS4B则综合了发电机转子转速和有功功率两种输入信号，可以避免有功功率快速变化时而引起的无功功率波动，较好地消除“反调”现象。

（2）多频段PSS4B又称为多频段稳定器，具有3个频段，每个都可以单独调节增益、滤波器、补偿相位、输出限幅等环节参数，可以为不同的振荡模式提供合适的阻尼。其频段按照低频振荡范围划分为低、中、高三段。低频段（0.04 Hz～0.10 Hz）主要针对电力系统的全局模式设计；中频段（0.1 Hz～1.0 Hz）主要针对区域间振荡模式设计；高频段（1 Hz～4 Hz）主要针对局部振荡模式或厂站机组间的低频振荡模式而设计。显然，仅用一台PSS4B就可以对多个振荡模式产生良好的抑制效果。而之前出现的稳定器均只有一个频段，高频段和低频段难以兼顾［7］。

对于PSS4B的参数，虽然表面上看起来很繁琐复杂，但实际上常用一种简便的参数设置方法，即把PSS4B的3个频段设置成对称的带通滤波器形式，各频段滤波器在中心频率处增益最大，且相位为零，便于进行超前滞后计算。实际工程中，还需要根据发电机组及其在系统中的位置进行现场调试设置工作［2-5］。

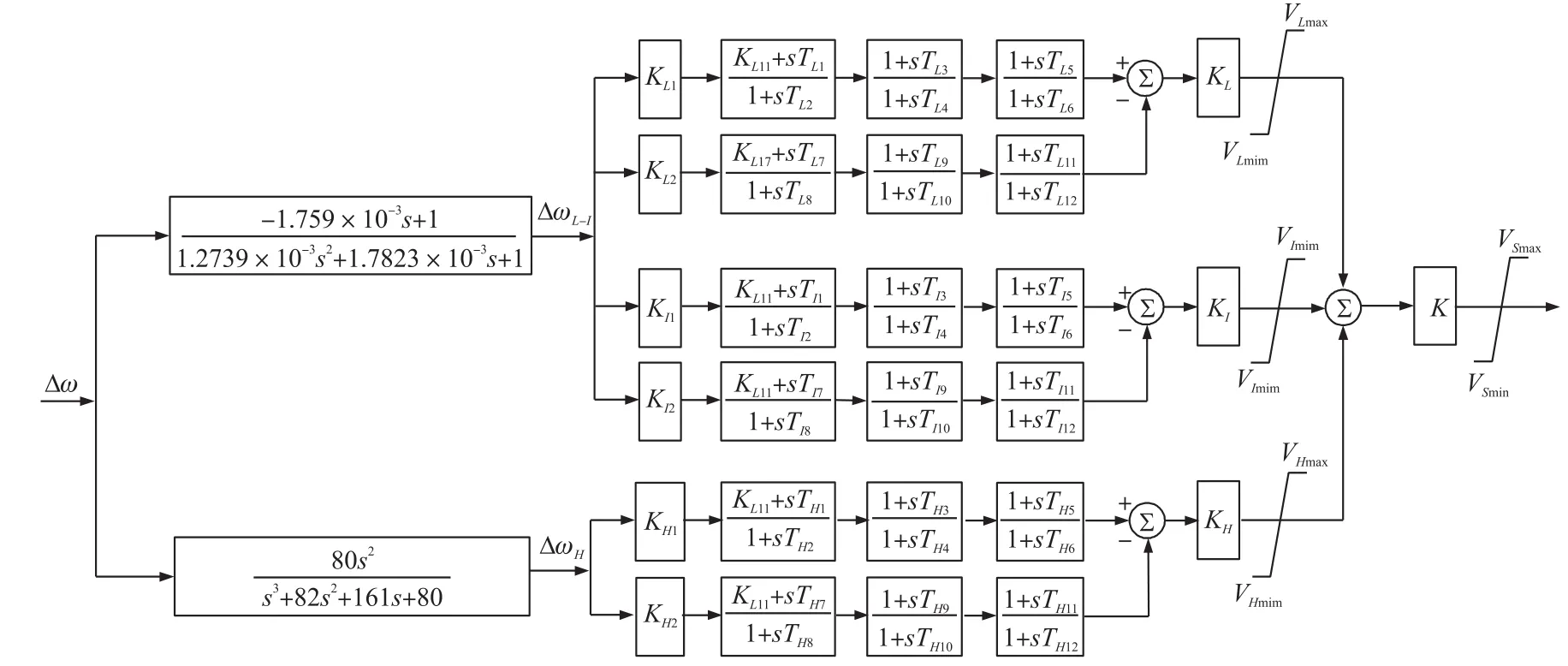
图3PSS4B数学模型

PSS4B各频段中心滤波器参数设置满足在中心频率处增益最大且相位为零，计算公式如下：

式中，FL是中心频率，R是比例常数，IEEE推荐取1.2，此时KL1=KL2=66。

通过以上整定，在中心补偿频率处的放大倍数是1，而整个分支的放大倍数为频段增益KL。各段中心滤波器和频段增益确定后，可以得到一个简单的PSS4B参数设置，但是各频段互相叠加，不能完全解耦，需要考虑其相互影响。

每个频段两级超前滞后环节参数设置将在上述中心滤波环节以及频段增益确定的基础上影响PSS4B最终的频率特性，设置上下分支完全相同，则可将其从两分支中提取出来，如图4所示。因此，需要整定的PSS4B参数归纳为：

低频段：FL、KL、TL1、TL2、TL3、TL4

中频段：FI、KI、TI1、TI2、TI3、TI4

高频段：FH、KH、TH1、TH2、TH3、TH4

总增益：K

图4PSS4B模型变型

对于PSS4B的参数优化仍然基于相位补偿法，采用改进粒子群算法进行优化。通过对PSS4B模型以及参数分析，得知对比传统PSS2A/B，PSS4B的3个频段多出了3个中心滤波环节，且中心频率范围相隔较近，通过各频段增益环节输出后对其他频段相频特性影响最大。为了提高优化效率，减小各频段之间的耦合影响，考虑将参数划分为两个部分，通过两次相位补偿对参数进行优化。首先按照一定的补偿目标优化对频段频率特性影响最大的中心滤波环节以及频段增益，然后在第1次相位补偿的基础上按照最终有补偿频率特性目标范围优化超前/滞后环节时间常数。参数划分如图5所示（以低频段为例），虚线框中部分为首次优化的参数，其他部分为二次优化的参数。

2.2基于粒子群的PSS参数优化［10］

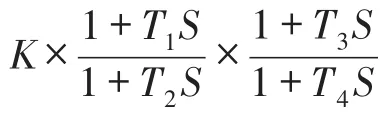
优化目标函数可以描述为式（8）：

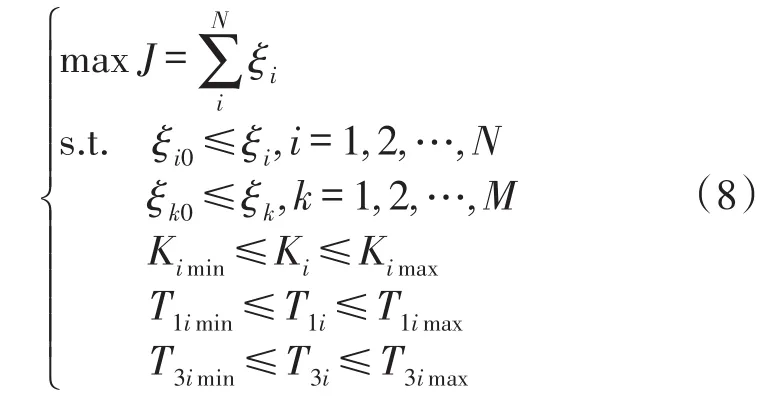
其中ξi是影响小水电群送出的主导低频振荡模式的阻尼比，ξk是其它主导低频振荡模式的阻尼比，ξi0和 ξk0是阻尼比原始值；Ki，T1i和T3i是第i台机组的待优化参数。

（1）参与PSS优化机组的筛选

根据机组参与主导振荡模式的程度进行排序，选择其中影响大的机组进行PSS参数优化。

一般的方法是利用参与因子进行机组的筛选。参与因子可以表示为 pki=φki×ψik，表示模式i中第k个状态变量的相对参与程度。PSS在抑制低频振荡时，主要关注的状态变量是发电机转子角频率ω。可以选择ω对主导振荡模式有较大参与因子的机组参与PSS优化。

由于机组PSS装置的输入是机组的ω和PG，输出量Vpss叠加在机组的励磁系统输入端，从模式的可控性和可观性角度，利用机组ω对模式的可观性以及PSS输出对模式的可控性的留数指标，分析机组对主导振荡模式的参与程度，可以取得更好的效果。

（2）改进的寻优策略

优化目标要求机组PSS参数优化结果要满足主导振荡模式阻尼比大于等于其原始值的约束条件。而在粒子群寻优过程中，由于一些机组可能参与多个主导振荡模式，因此其PSS参数可能会使一些主导振荡模式阻尼比增大，而导致另一些主导振荡模式阻尼比小于其原始值的情况，从而导致大量不可行解出现。

如果在寻优过程中仅利用可行解来寻找全局最优解，而不考虑不可行解在粒子群飞行中的引导作用，可能会降低搜索效率。而且在可行域占搜索空间比例很小或最优解位于边界附近情况下，一些不可行解可能更接近全局最优解，包含更多有用信息，如果利用不可行解的信息来引导粒子群飞行，有利于寻找全局最优解。为此本文提出一种改进的搜索策略。

改进的策略为，粒子群找到的个体或全局极值，虽然不满足约束条件，但只要在容许范围内，即满足g≤ε的条件，仍可以作为个体极值或全局极值的速度和位置更新。

该策略可以使寻优过程在迭代的初期，允许一些满足容忍度阈值的不可行解提供信息给粒子群，随着迭代进行，容忍度阈值不断减小，对可行解的要求越来越高，有利于粒子群在可行解的指引下寻优。

2.3第一次相位补偿

采用PSO算法进行第1次相位补偿，种群中粒子表示为（FL，KL，FI，KI，FH，KH），补偿目标为对无补偿频率特性实现适度预补偿，并且为第2次相位补偿留有一定裕度。目标函数为式（9）：

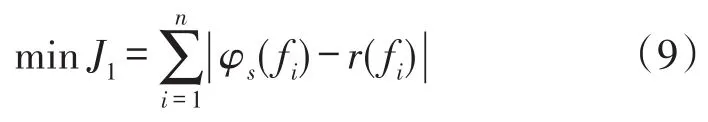
式中，φs为只包含首次优化参数的PSS4B的相频特性，r为各频段目标补偿度，由各频段无补偿频率特性决定。

约束条件为：

（1）当 0.04 Hz＜fi＜0.1 Hz时：r的取值范围为［0°，10°］；

当0.1 Hz＜fi＜1 Hz时：r的取值范围为［10°，15°］；

当1 Hz＜fi＜4 Hz时：r的取值范围为［10°，20°］。

（2）FL的取值范围为［0.01，0.1］；

FI的取值范围为［0.1，1］；

FH的取值范围为［1，10］；

KL，KI，KH的取值范围为［1，10］。

2.4第二次相位补偿

基于第1次相位补偿，整定了3个频段的中心频率以及增益，第2次相位补偿将优化整定3个频段的超前-滞后环节参数。

仍然采用PSO算法，为了提高优化效率采用分频段优化，即按照低频段、中频段、高频段的顺序，通过3次PSO寻优分别整定各频段的超前-滞后环节时间常数T1，T2，T3，T4。

种群中每个微粒代表一组时间常数（T1，T2，T3，T4），优化的目标函数按照顺序分别为：

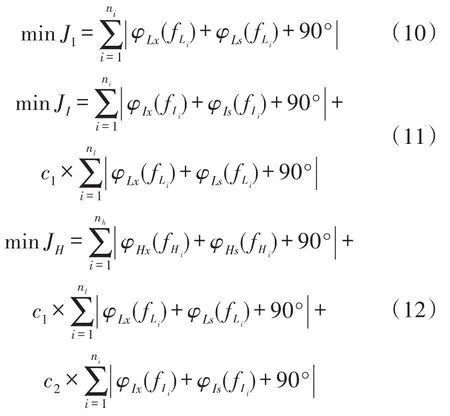
约束条件为：

式中，将无补偿频率特性按照3个频段划分为φLx，φIx，φHx，φLs，φIs，φHs为依次加入 3个频段超前-滞后环节后PSS4B对应频段的相频特性，φL0，φI0，φH0为 3个频段对应的有补偿频率特性，c1，c2为某频段的补偿环节对前面频段频率特性的影响因子。

2.5总增益K整定

相位补偿法是从频率特性上来优化整定PSS4B相关参数，最后总增益的整定为在该基础上确定PSS4B附加阻尼转矩的阻尼系数，并不影响PSS4B的相频特性。目前通用的方法即为临界增益法。临界增益试验的方法如下：在选定的相位补偿参数下，缓慢增大PSS的增益，同时仔细观察励磁系统各可观测量的变化，直到观察到不稳定现象为止，将放大倍数确定为临界增益的1/3～1/2，即认为是最佳增益［9］。

3　算例分析

为了对优化结果有效性进一步检验，图5选取PSS2B典型参数、PSS2B优化参数、PSS4B典型参数、PSS4B优化参数和进行幅相频特性对比，对比其波特图可以明显看到，不同的PSS在0.1 Hz～5.0 Hz有非常相似的相频响应的波形，然而PSS4B优化的增益在关键的区间模型0.1 Hz～1.0 Hz频率上表现更好，鲁棒性强。

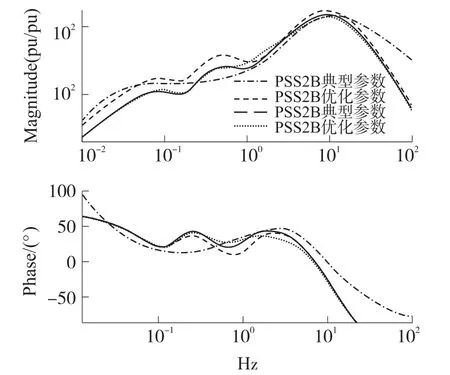
图5　PSS2B和PSS4B幅频相频波特图对比

对ABB公司的UNITROL 6800的励磁调节器的典型PSS4B和优化PSS4B模型利用RTDS进行了仿真测试，被试机组有功功率300 MW，无功功率20 Mvar，分别在1.2 Hz、1.0 Hz、0.8 Hz、0.6 Hz、0.4 Hz、0.2 Hz和0.1 Hz的扰动，进行3%的定子电压扰动，在典型PSS4B和优化PSS4B模型的试验录波数据如表1、表2所示，试验波形如图6、图7所示。

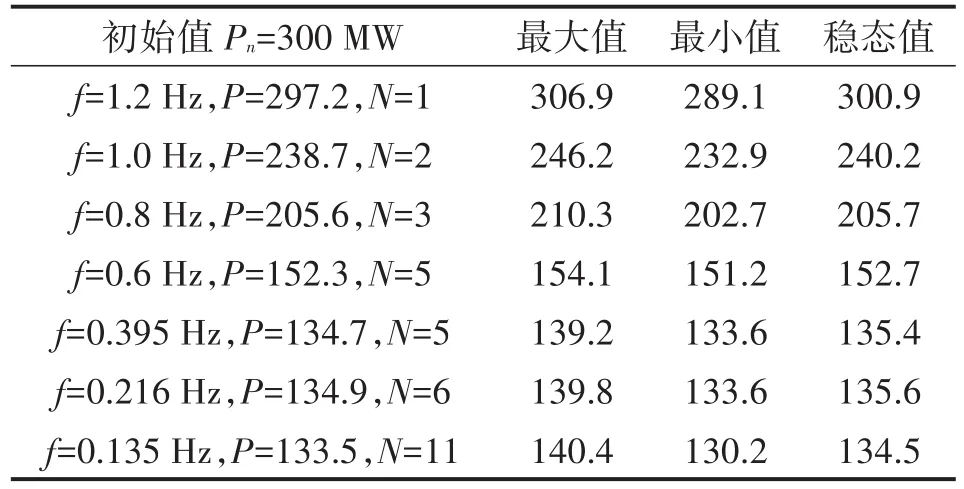
表1　典型PSS4B模型测试数据

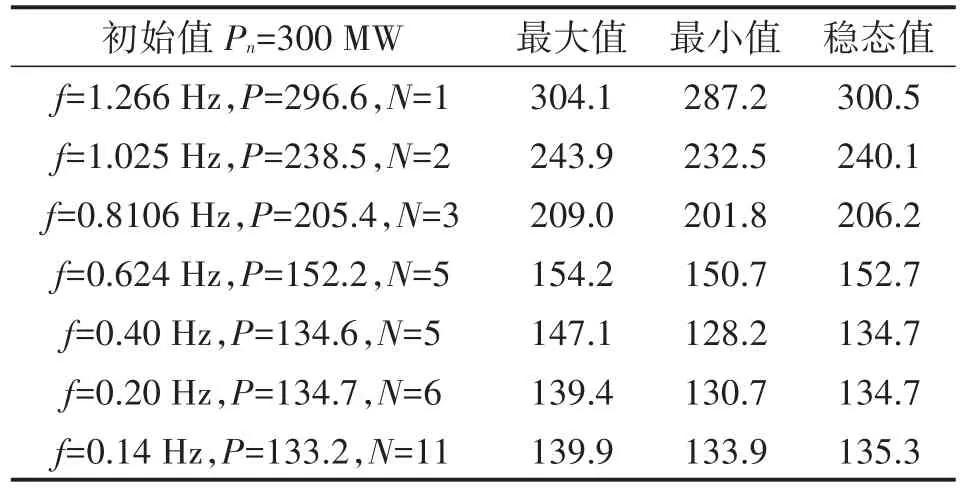
表2　优化PSS4B模型测试数据

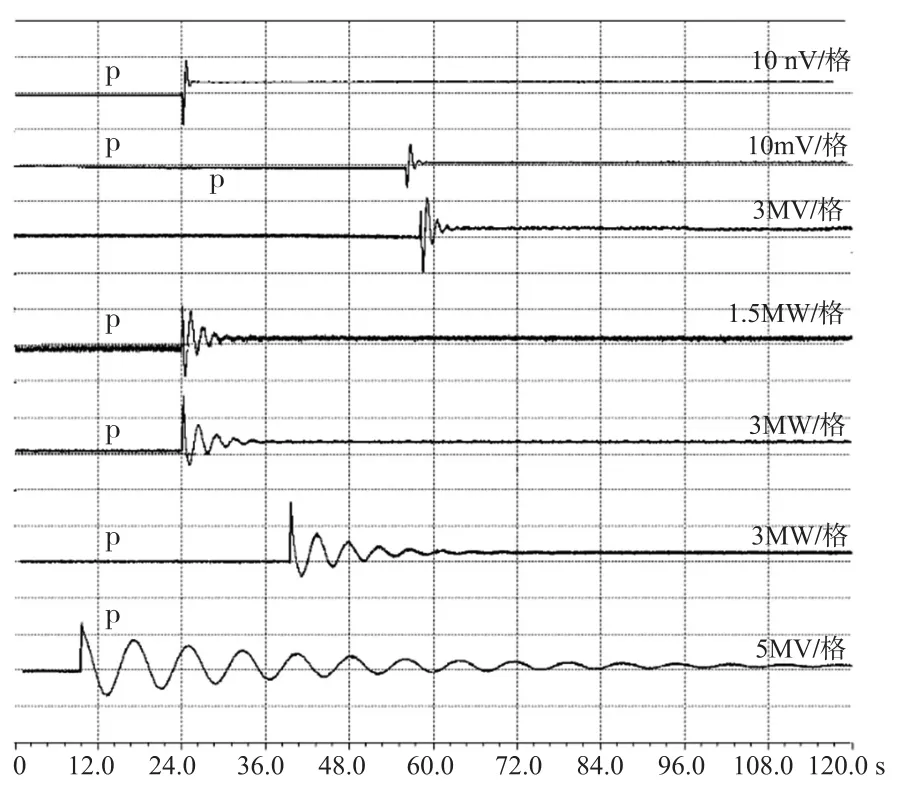
图6　典型PSS4B模型在不同频率扰动下性能检测及抑制效果

图7　PSS4B优化模型在不同频率扰动下性能检测及抑制效果

有仿真试验录波结果来看，PSS4B对于有功振荡的抑制效果，无论在高、中、低频振荡模式下均能提供最佳的阻尼效果，随着频率降低，PSS4B较PSS2B对各振荡模式阻尼效果改善更明显。进一步对上述系统进行试验研究，对无PSS、PSS2A参数、PSS2B参数、PSS4B优化参数进行时域和频域特性对比，如图8和图9所示。

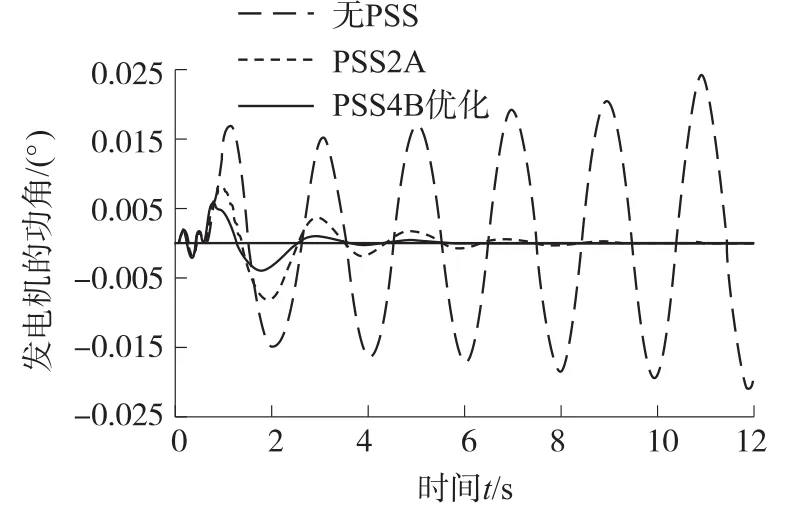
图8　无PSS、PSS2A和PSS4B优化模型对比

图9　无PSS、PSS2B和PSS4B优化模型对比

通过无PSS系统、PSS2A、PSS2B和PSS4B参数优化对比，试验结果表明，PSS2A和PSS2B模型对宽频段范围内调整相位不能很好的适应，PSS4B可以在更大的频率范围内提供更好的灵活性来获得更好的调节性能。采用PSS4B参数优化方法的可以提升系统反应速度，缩小时间，给系统提供更大的阻尼效果。

4　结论

本文采用相位补偿法和粒子群优化算法对PSS4B参数进行协调优化，实现了PSS4B在整个工作频段上良好的补偿效果，解决了目前PSS4B参数整定困难的问题，具有一定工程意义。优化后的PSS4B模型对于有功振荡的抑制效果，无论在高、中、低频振荡模式下均能提供最佳的阻尼效果，随着频率降低，PSS4B较PSS2B对各振荡模式阻尼效果改善更明显。

经过长期的发展，发电机励磁控制已经成熟，从励磁的发展方向看，在控制技术方面有采用非线性及人工智能的、在元器件方面有采用全控型电力电子元件的，但有一个问题受到了忽视，就是励磁系统自身故障的保护问题，目前仍然由分立的机组保护解决，对于此问题，励磁技术科研人员应承担更重要责任与义务。

［1］倪以信，陈寿孙.动态电力系统的理论与分析［M］.北京：清华大学出版社，2002：1-10.

［2］尚超，丁坚勇，马曦.新型电力系统稳定器PSS4B的分析与仿真［J］.华东电力，2013（3）：575-578.

［3］汤伟.基于MATLAB的PSS的参数计算与仿真［D］.哈尔滨：哈尔滨理工人学，2010.

［4］华国辉，赫卫国，赵大伟，等.电力系统稳定器PSS4B模型的研究与实现［C］//2010年中力系统自动化学术会交集.

［5］管秀鹏，程林，孙元章.基于Prony方法的大型互联电网PSS参数优化设计［J］.电力系统自动化，2006，30（25）：7-11.

［6］Kamwa I，Grondin R，Trudel G.IEEE PSS2B Versus PSS4B：The Limits of Performance of Modern Power System Stabilizers.Power Systems，IEEE Transactions on［J］.2005，20（2）：903-915.

［7］Grondin R，Kamwa I，Trudel G.Modeling and Closed-Loop Validation of a New PSS Concept，the Multi-Band PSS［C］//Power Engineering Society General Meeting，2003，IEEE，2003：1803-1809.

［8］Hua Guanghui，He Weiguo，Zhao Dawei.Research and Implementation on Power System Stabilizer PSS4B Model［C］//Electricity Distribution（CICED），2010 China International Conference on，2010：1-4.

［9］朱良合，李文意，毛承雄，等.新型电力系统稳定器模型分析及参数协调优化［J］.水电能源科学，2014，32（6）：171-175.

［10］刘蔚，赵勇，吴琛，等.一种提高多小水电群送出能力的PSS参数协调优化方法［J］.电力系统保护与控制，2015，43（4）：44-50.

［11］牛振勇，杜正春，方万良.基于进化策略的多机系统PSS参数优化［J］.中国电机工程学报，2004，24（2）：22-27.

［12］石辉，张勇军，徐涛.我国智能电网背景下的低频振荡应对研究综述［J］.电力系统保护与控制，2010，38（24）：242-247.

［13］马燕峰，赵书强.基于在线辨识和区域极点配置法的电力系统低频振荡协调阻尼控制［J］.电工技术学报，2012，27（9）：117-123.

［14］夏潮.并行电力系统稳定器的研究［D］.中国电力科学研究院，2007.

［15］邱磊，王克文，李奎奎，等.多频段PSS结构设计和参数协调［J］.电力系统保护与控制，2011（5）：102-107.

［16］夏潮，刘增煌，朱方，等.两分支分段补偿的并行电力系统稳定器［J］.中国电机工程学报，2010（19）：20-25.

［17］王克文，李衍，倪相生.相位补偿法设计双频段PSS［J］.电力系统及其自动化学报，2009（1）：1-7.

［18］杜文娟，王海风，曹军.PSS就地相位补偿法的模型和理论［J］.中国电机工程学报，2012（19）：36-41.

［19］杨立环，徐峰，胡华荣，等.电力系统稳定器PSS2A现场试验及参数整定［J］.电力系统保护与控制，2010（1）：112-114.

［20］祁万春，房鑫炎.基于混合粒子群优化算法的PSS参数优化［J］.继电器，2005（13）：21-24.

［21］崔志华.微粒群优化算法［M］.科学出版社，2011.

［22］刘洲洲，李艳平.基于量子粒子群优化算法的压缩感知数据重构方法［J］.传感技术学报，2015，28（6）：836-841.

［23］吴雅静，马珺.基于提升小波与粒子群相结合的混沌信号降噪［J］.电子器件，2014，37（6）：1093-1097.

［24］王超，李森.变参数QPSO算法优化神经网络的短期电力负荷预测［J］.电子器件，2014，37（4）：782-786.

［25］刘东，田雨波.基于改进粒子群算法的EBG结构优化设计？［J］.电子器件，2015，38（2）：38.

［26］沈鑫，王昕，赵艳峰，等.基于单周控制的并网逆变器在云南电网中的研究应用［J］.电子器件，2013，36（5）：722-727.

［27］沈鑫，曹敏，王昕，等.智能变电站的时钟同步准确性及稳定性研究［J］.电子器件，2015，38（3）：655-660.

［28］王昕，刘清蝉，沈鑫，等.基于电容电流的高准确度CVT谐波测试系统研制及运用［J］.电子器件，2014，37（6）：1221-1227.

沈鑫（1981-），男，云南人，云南电网有限责任公司电力科学研究院，博士研究生，高级工程师，昆明市第十三批学术和技术带头人，主要研究方向为电能计量和智能电网技术，23755803@qq.com；

马红升（1978-），男，云南人，云南电网公司有限责任公司，硕士，高级工程师，主要研究方向为电力系统稳定分析与控制技术。

A Method of PSS4B Parameters Optimization Based on the Phase Compensation Method and Particle Swarm Algorithm*

SHEN Xin*，MAHongsheng，LI Shilin，WANG Xin，LIU Qingchan
（Yunnan Electric Power Research Institute；Kunming 650217，China）

With the development of power grid scale，power system low frequency oscillation is becoming an increasingly outstanding problem.Power system stabilizer is one of the effective measures which can solve the low frequency oscillation.Aiming at some problems existing in using of PSS，optimum research on the model parameters of power system stabilizer，based on the phase compensation method and particle swarm optimization algorithm.The RTDS is used to establish the simulation experiment，after optimized the model parameters of the wild band power system stabilizer.The results show that optimized PSS4B can meet the requirements of multiple frequency bands，and effectively suppress lowfrequency oscillation.

power system stabilizer（PSS）；phase compensation method；particle swarm optimization（PSO）；multiband；parameter optimization

TM712；TM44

A

1005-9490（2016）05-1244-07

项目来源：云南省教育厅重大专项研究项目（2015Z014）

2015-08-31修改日期：2015-10-17

EEACC:811010.3969/j.issn.1005-9490.2016.05.043