一种新的基于扩展星型结构的系统级故障诊断算法

周宁，梁家荣

（广西大学计算机与电子信息学院，广西南宁530004）

一种新的基于扩展星型结构的系统级故障诊断算法

周宁，梁家荣*

（广西大学计算机与电子信息学院，广西南宁530004）

网络系统级故障诊断是一种重要的针对网络节点进行故障诊断的方法.通过对网络系统级故障诊断的PMC模型和MM模型的t可诊断性进行分析，在确定的网络拓扑结构中构造扩展星型结构，利用图论的方法对给定的PMC模型和MM模型下的症状进行分析和论证，判断扩展星型结构根节点的状态.最后基于扩展星型结构判断网络节点状态的证明结果，提出一种新的针对已确定系统诊断度、并能构造出扩展星型结构的多处理器网络系统的系统级诊断算法——扩展星型结构算法.通过理论证明和实验结果表明：这种算法能够简单、快速并且正确地识别出处理器网络系统的故障节点，其时间复杂度为O（N），N表示处理器网络系统的节点个数.

系统级故障诊断；PMC模型；MM模型；扩展星型结构；多处理器网络系统

0　引言

随着超大规模集成电路技术的飞速发展，一个多处理器网络系统可能包含几百个甚至几千个处理器；互连网络高速频数的交换信息及系统硬件规模的不断扩大，使得网络的处理器出现故障是不可避免的.为了确保网络可靠性，在系统投计时应该考虑其有能力区分故障节点和无故障节点，以便用无故障节点替换故障节点.在故障诊断的过程中，虽然诊断的最终目标是要找出结点中发生故障的逻辑门或芯片，对它进行修复或更换，但如果一开始就把诊断范围定位于此，不仅需要大量的诊断信息，难以达成目标，而且可能舍本逐末，无法确定故障；因此，需要提高诊断级别，将故障定位到系统级，即只需要识别出发生故障的结点机或通信链路，这样不仅极大地减少了故障诊断所需要的信息，降低了测试费用和诊断难度，而且完全能够满足解决系统容错性问题和维护问题对诊断功能的要求.

1967年Preparata等［1］首次提出了系统级故障诊断的概念和方法，并提出了系统级诊断模型，即PMC模型.PMC模型认为，让系统中的每一个节点去测试它的邻居节点，这种测试可能是一套微指令，或者是电子信号配合相应的硬件.如果一个节点认为另一个节点是有故障的，那么给出的测试结果为1；反之给出的测试结果为0，并约定一个无故障的节点所作出的评估总是可靠的，而有故障的节点给出的评估是不可靠的；所有测试结果的集合称之为系统的症状.关于PMC模型下相关的故障诊断度问题已有大量成果［2－7］.

考虑到PMC模型在处理一些复杂网络时存在的不足，如对于具有高结点度的网络，利用PMC模型进行诊断，会耗费更多的测试资源，文献［8］提出了另一种系统级的故障诊断模型，称之为MM模型；其后，1992年文献［9］进行了改进，并提出了一种特殊情况的比较模型MM＊故障模型.MM模型假定一个节点将同样的测试任务分配给它的2个邻居节点，并比较这2个邻居节点的输出.如果2个邻居节点的输出结果一致，则认为它们是无故障的；否则它们是有故障的.比较模型不再采用测试的方法来获取测试结果，而是采用一种更实际的比较机制.由于比较2个结点的处理结果比结点间相互测试更容易，因此，MM比较模型与PMC模型相比更易于实现.对比较模型下的网络故障诊断理论的研究也取得了不少成果［10－12］.

在网络的故障诊断理论研究中，故障诊断度和故障诊断算法是2个重要的内容.人们对PMC模型下的故障诊断算法研究已取得了不少成果，如Dahbura等［13］利用最小覆盖集及最大匹配集理论的时间复杂度为O（N2．5）的故障诊断算法；Kameda等［14］提出了一个基于分支限界法的故障诊断算法，该算法能够在O（N3）的时间内确定系统的所有故障结点；另外Sullivan［15］提出了一个时间复杂度为O（t3＋｜E｜）的诊断算法.而在MM模型下的已有算法研究成果中，Sengupta等［9］提出了时间复杂度为O（N5）的算法；Yang等［16］则针对超立方体网络提出了更为有效的、时间复杂度为O（N×Δ3×δ）的诊断算法.

在已有系统级诊断算法的研究成果中，可以发现这类算法或者时间复杂度较高，或者对网络的拓扑结构有限定性的要求，或者算法的诊断过程较为复杂，难以实现.考虑到星型结构在大多数网络中存在，提出一种新的适用于已确定诊断度并且能够构造出扩展星型结构的多处理器网络系统的系统级诊断算法，即扩展星型结构算法.该算法将网络中的所有节点都构造一个扩展星型结构，然后遍历网络的所有节点并利用本文的证明结论判断网络节点的状态，从而获得无故障节点的集合和有故障节点的集合（该算法的流程框架如图1所示）.扩展星型结构算法的特点是：1）基于PMC模型和MM模型；2）适用于能构造出扩展星型结构的t－可诊断系统；3）能够快速、简单、正确地诊断出系统中的所有故障节点.这种方法不需要使用专门的测试设备，在不增加系统额外成本的情况下就可以实现系统的快速自诊断.从这个意义上讲，这样的算法对网络故障诊断理论是一种重要的补充，对网络的故障诊断有重要的理论意义和应用价值.

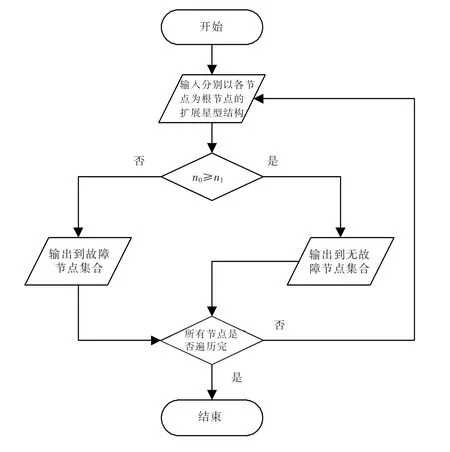
图1　扩展星型结构算法流程图Fig．1 The algorithm of the extended star structure

1　预备知识

文中，用有向图G来表示一个互连网络，其中V（G）和E（G）分别表示图G的顶点集和边集.k（G）表示图G的顶点连通度.

定义1［1］一个系统是t－可诊断的，只要系统中的故障节点数目不超过t个，那么系统中所有故障节点都能够被正确地识别出来.

在PMC模型中，令有向图G＝（V，E）表示一个系统，其中V表示系统中所有节点的集合，E表示系统中所有通信连接的集合.对于一对相邻的节点u，v∈V，有序对（u，v）表示节点u测试节点v.如果节点u是正确的（错误的），那么测试结果为0（1），记为γ（u，v）＝0（γ（u，v）＝1）.正确的节点所做的评估总是可靠的，而错误的节点所做的评估是不可靠的（如图2所示）.

在MM模型中，令有向图G＝（V，E）表示一个系统，其中V表示系统中所有节点的集合，E表示系统中所有通信连接的集合.假定一个节点将同样的测试任务分配给它的2个邻居节点，并比较这2个邻居节点的输出.用（u；v，w）来表示节点u发送相同的任务给邻居节点v和w去执行并观察它们的运行结果.如果节点v和w的运行结果不一致的（一致），那么测试结果为1（0）（如图3所示）.

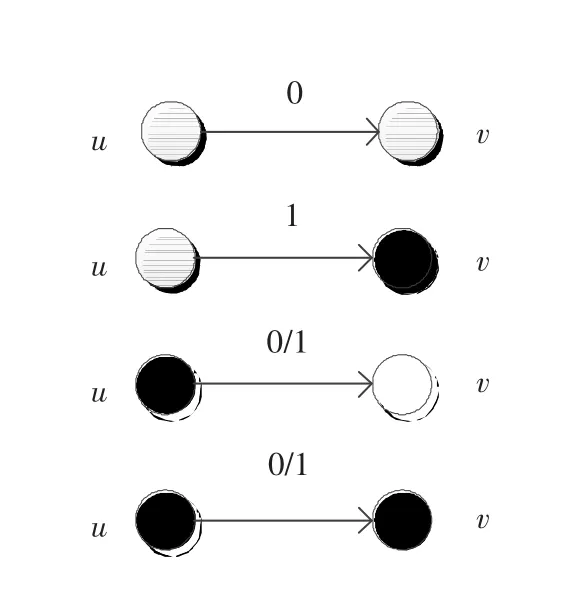
图2　PMC模型Fig．2 The PMC model

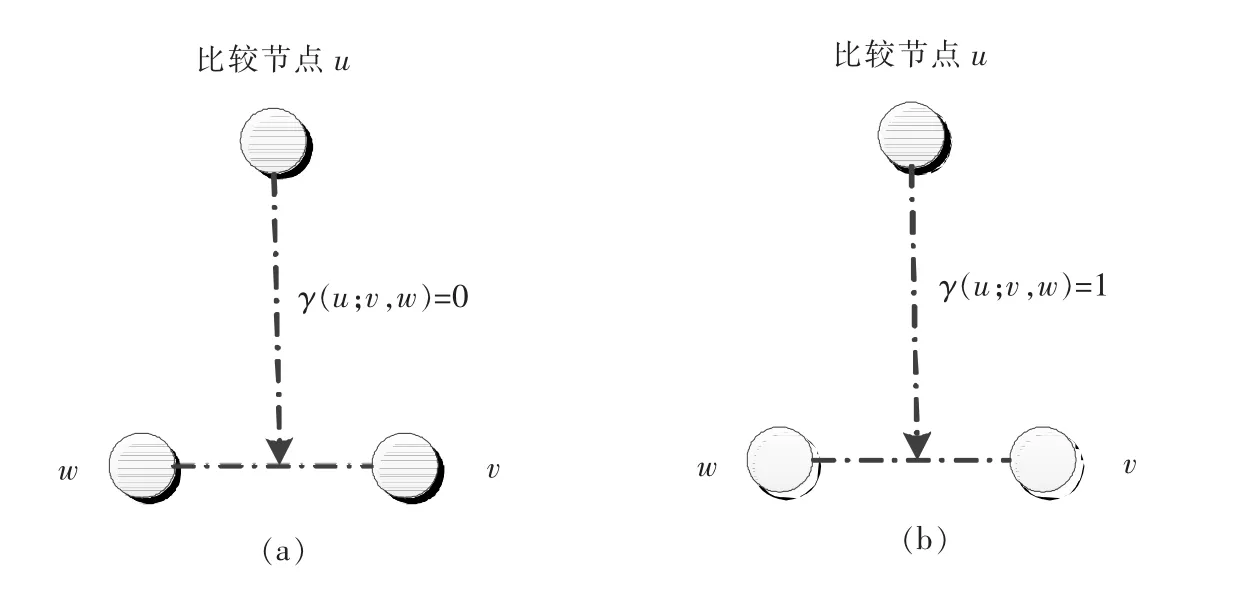
图3　MM模型Fig．3 The MM model

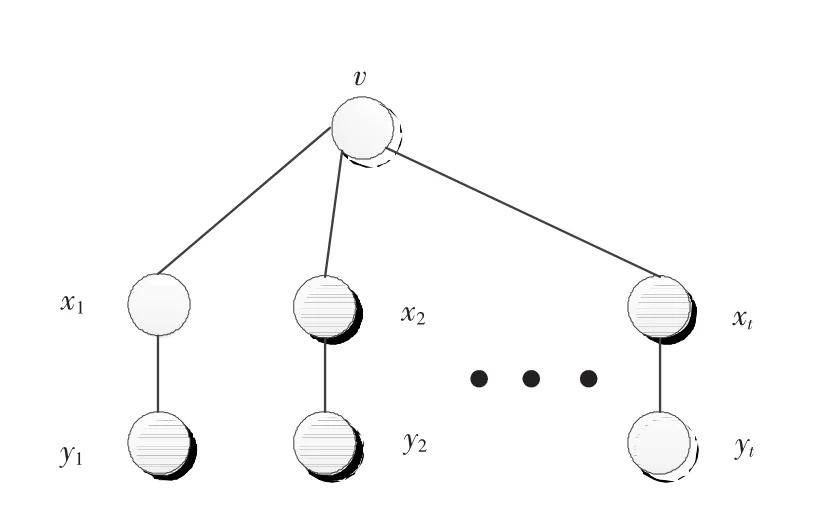
图4　T型扩展星型结构Fig．4 Type T extended star structure

2　在PMC下的扩展星型结构算法

2.1相关定义

定义2令G＝（V，E）表示一个图，v∈V，t是一个≥1的整数.用T（v，t）＝（V（v，t），E（v，t））表示一个图G中以v为根节点按1到t次序扩展的星型结构的子图，其中V（v；t）＝｛v｝∪｛xi，yi，｜1≤i≤t｝以及E（v；t）＝｛｛v，xi｝，｛xi，yi｝｜1≤i≤t｝（如图4所示）.

算法名称：DVUPMC（G，v）

输入：对于图G的任意一个节点v，存在以v为根节点的星型扩展结构的子图T（v，t）.

输出：v的故障状态.算法输出用0表示节点v无故障，用1表示节点v有故障.

算法开始：

1）t≤deg G（v），deg G（v）表示v的度数；

2）构造一个以v为根节点按1到t次序星型扩展结构的子图T（v，t）；

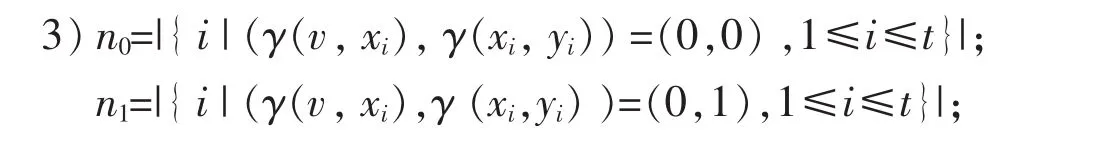
4）如果n0≥n1返回0，否则1.

算法结束.

定理1令G＝（V，E）表示一个图，v∈V（G），t≤deg G（v）.假设图G中存在以v为根节点并且按1到t次序扩展的星型结构的子图，即T（v，t），那么只要子图T（v，t）中故障节点的个数不超过t个，算法DVUPMC（G，v）能够完全正确地判断节点的故障状态.

证明：令：

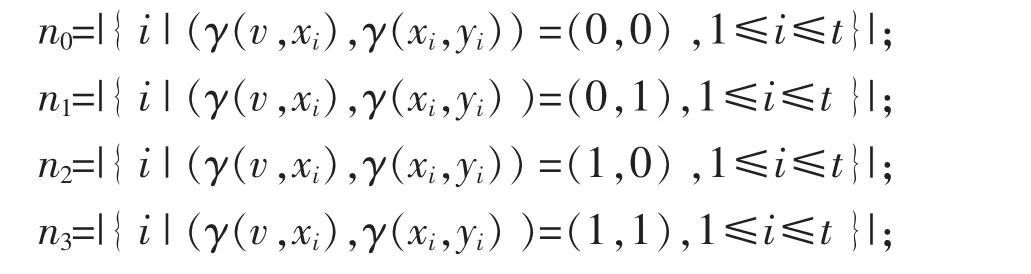
显然，依照假定有：t＝n0＋n1＋n2＋n3.

首先，考虑节点v为故障节点的情况.用反正法证明，有n0≥n1.由此可以得到在T（v，t）中的故障节点个数至少为2n0＋n1＋n2＋n3＋1，而2n0＋n1＋n2＋n3＋1≥n0＋n1＋n2＋n3＋1＝t＋1，这与题设的T（v，t）中故障节点个数不超过t个相矛盾；因此，当节点v为故障节点时，有n0＜n1.

其次，考虑节点v为无故障节点的情况.用反正法证明，有n0＜n1.由此可以得到在T（v，t）中的故障节点个数至少为2n1＋n2＋n3＋1，而2n1＋n2＋n3＋1≥n0＋n1＋n2＋n3＋1＝t＋1，这与题设的T（v，t）中故障节点个数不超过t个相矛盾；因此，当节点v为无故障节点时，有n0≥n1.定理得证.

2.2多处理器网络自诊断算法

算法名称：t－PMC－DIAG

输入：一个在PMC模型下，由故障节点个数不超过t的具体扩展星型结构的多处理器的网络产生的症状γ.

输出：一个序列（H，F），H表示被诊断为无故障的节点的集合，F表示被诊断为有故障的节点的集合.

Step1初始化H和F，即H←φ，F←φ；U＝V（G），其中φ表示空集合；

Step2对于多处理器网络中的每一个节点v，构造一个扩展星型结构，即T（v，t）；然后用算法DVUPMC（G，v）判断节点v的状态，如果输出的状态为0，则将节点v添加到集合H中，即H←H∪｛v｝；

否则将节点v添加到集合F中，即F←F∪｛v｝；

Step3返回序列（H，F）.

定理2在PMC模型下，在具体扩展星型结构的多处理器网络运行t－PMC－DIAG的时间复杂度为O（N），其中N表示多处理器网络的节点个数.

证明：Step1的时间复杂度为O（1），Step2中，因为每个节点都要构造一次扩展星型结构，假设多处理器网络的节点总数为N个，那么该步骤的时间复杂度为O（N），Step3的时间复杂度为O（1）.综合Step1～Step3，整个算法的时间复杂度为O（N）.

3　在MM模型下的扩展星型结构算法

定义3令G＝（V，E）表示一个图，v∈V，t是一个≥1的整数.用Π（v，t）＝（V（v，t），E（v，t））表示一个图G中以v为根节点按1到t次序扩展的星型结构的子图，其中V（v；t）＝｛v｝∪｛xi，yi，zi，wi｜1≤i≤t｝以及E（v；t）＝｛｛v，xi｝，｛xi，yi｝，｛yi，zi｝，｛zi，wi｝｜1≤i≤t｝（如图5所示）.

算法名称：DVUMM（G，v）

输入：对于图G的任意一个节点v，存在以v为根节点的星型扩展结构的子图Π（v，t）.

输出：v的故障状态.算法输出用0表示节点v无故障，用1表示节点v有故障.

算法开始：

1）t≤deg G（v），deg G（v）表示v的度数；

2）构造一个以v为根节点，度为t的星型扩展结构的子图Π（v，t）；

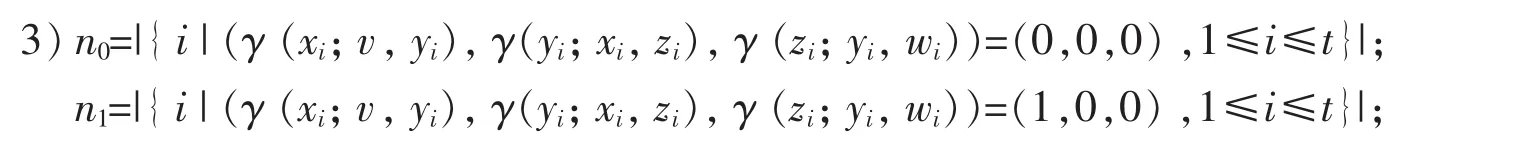
4）如果n0≥n1，返回0；否则1.

算法结束.

定理3令G＝（V，E）表示一个图，v∈V（G），t≤deg G（v）.假设图G中存在以v为根节点并且按1到t次序扩展的星型结构的子图，即Π（v，t），那么只要子图Π（v，t）中故障节点的个数不超过t个，算法DVUMM（G，v）能够完全正确地判断节点的故障状态.

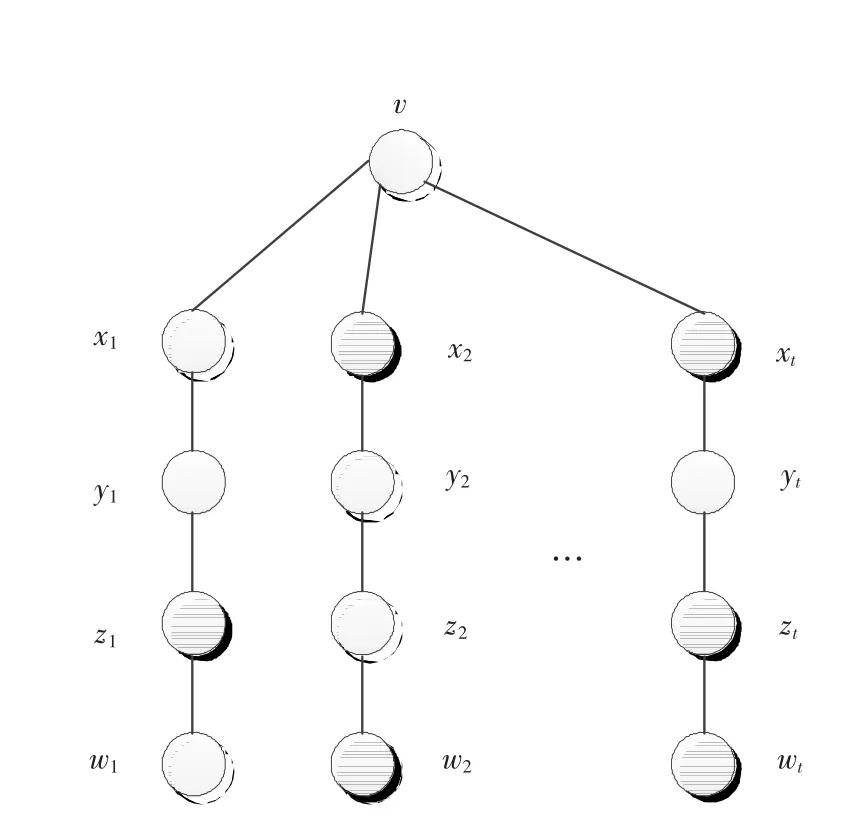
图5　Π型扩展星型结构Fig．5 Type Π extended star structure

证明：令：

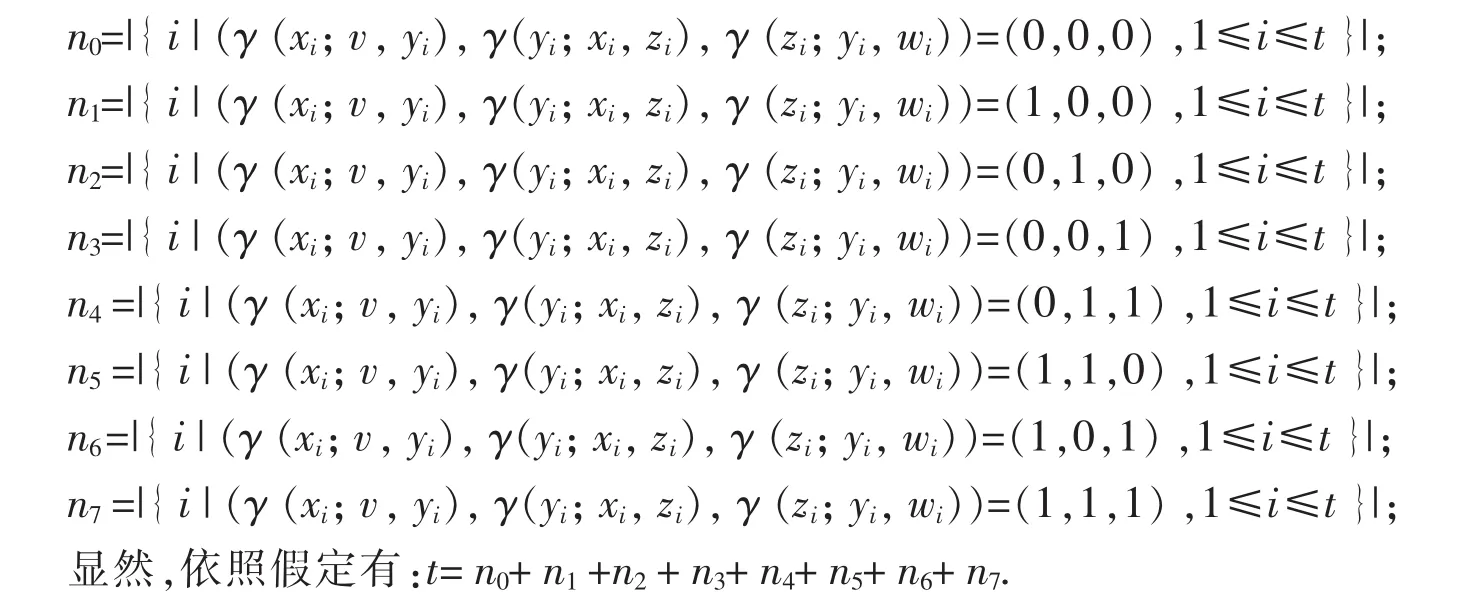
首先，考虑节点v为故障节点的情况.用反正法证明，有n0≥n1.由此可以得到在Π（v，t）中的故障节点个数至少为3n0＋n2＋2n3＋2n4＋n5＋n6＋2n7＋1；而n0＋n2＋2n3＋2n4＋n5＋n6＋2n7＋1≥（n0＋n1＋n2＋n3＋n4＋n5＋n6＋n7）＋2n0＋n3＋n4＋n7＋1≥t＋1．这与题设的Π（v，t）中故障节点个数不超过t个相矛盾；因此，当节点v为故障节点时，有n0＜n1.

其次，考虑节点v为无故障节点的情况.用反正法证明，有n0＜n1.由此可以得到在Π（v，t）中的故障节点个数至少为2n1＋n2＋n3＋n4＋n5＋n6＋n7；而2 n1＋n2＋n3＋n4＋n5＋n6＋n7≥（n0＋n1＋n2＋n3＋n4＋n5＋n6＋n7）＋1≥t＋1，这与题设Π（v，t）中故障节点个数不超过t个相矛盾；因此，当节点v无故障节点时，有n0≥n1.定理得证.

下面是在MM模型下针对具体扩展星型结构的多处理器网络的自诊断算法：

算法名称：t－MM－DIAG

输入：一个在MM模型下，由故障节点个数不超过t的具体扩展星型结构的多处理器网络产生的症状γ.

输出：一个序列（H，F），H表示被诊断为无故障的节点的集合，F表示被诊断为有故障的节点的集合.

Step1初始化H和F，即H←φ，F←φ；U＝V（G），其中φ表示空集合；

Step2对于多处理器网络中的每一个节点v，构造一个扩展星型结构，即Π（v，t）中.然后用算法DVUMM（G，v）判断节点v的状态，如果输出的状态为0，则将节点v添加到集合H中，即H←H∪｛v｝，否则将节点v添加到集合F中，即F←F∪｛v｝；

Step3返回序列（H，F）.

定理4在基于MM模型下，具体扩展星型结构的多处理器网络运行t－MM－DIAG的时间复杂度为O（N），其中N表示多处理器网络的节点个数.

证明：Step1的时间复杂度为O（1），Step2中，因为每个节点都要构造一次扩展星型结构，假设多处理器网络的节点总数为N个，那么该步骤的时间复杂度为O（N），Step3的时间复杂度为O（1）.综合Step1～Step3，整个算法的时间复杂度为O（N）.

4　实验模拟

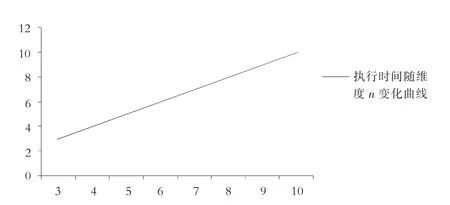
图6　算法的执行时间随维度n的变化情况Fig．6 The execution time of algorithm as dimension n

通过计算机模拟t－MM－DIAG算法和t－MM－DIAG算法的执行，对其正确性和性能进行评估.

首先，选择超立方体作为网络系统结构，已知n维的超立方体的诊断度为n并且能构造出扩展星型结构；接着，搭建运行算法的软硬件环境.选择的硬件为：戴尔Precision T7910系列工作站，软件为：Linux 64位操作系统，hadoop集群框架，VMware11虚拟机.在VMware11虚拟机中安装若干Linux 64位操作系统，并用hadoop框架搭建成一个集群，使它们构成一个超立方体网络；最后，将算法提交到hadoop集群构成的超立方体网络执行.从3维到10维的超立方体执行算法的时间复杂度如图6所示.表1表示从3维超立方体到10维超立方体故障节点被检测出来的个数.从实验结果可以印证t－MM－DIAG算法和t－MM－DIAG算法是完全正确的，并且相较于Dahbura等［13］提出的故障诊断算法有了大幅的提升.

表1　通过算法检测出的故障节点的数量Tab.1 The number of faulty nodes detected by the algorithm

5　结论

系统级诊断就是利用网络系统自身的节点识别出系统中其它节点的状态，进而将故障的节点替换或者从逻辑上删除.本文在PMC模型和MM模型下，分别提出了基于扩展星型结构的新的系统级诊断算法.该算法在系统中的故障节点个数不超过t情况下，为系统中的每个节点在系统范围内构造一个扩展星型结构，然后用DVUPMC算法或DVUMM算法获得节点的状态结构，进而获取整个系统的无故障节点集合和故障节点集合.通过实验模拟也验证了算法的正确性.

系统需要周期性的进入诊断模式，以确保系统能够掌握每一个节点的状态，不会将任务分配给错误的节点.系统级诊断是一个非常重要的研究领域，目前还有许多开放的研究点待研究.

［1］PREPARATA FP，METZE G.CHIEN RT.On the Connection Assignment Problem of Diagnosable Systems［J］．IEEE Transactions on Electronic Computers，1967，16（6）：848－854．

［2］LIANG JR，HUANG Y，YE LC．Diagnosabilities of Exchanged Hypercube Networks under the Pessimistic One－Step Diagnosis Strategy［J］．Journal of Systems Engineering an Electronics，2015，26（2）：415－420．

［3］Y E LC，L IANG JR．Five－Round Adaptive Diagnosis in Hamiltonian Networks［J］．IEEE Trans actions on Parallel and Distributed Systems，2015，26（9）：2459－2464．

［4］ZHU Q，GUO G，WANG D．Relating Diagnosability，Strong Diagnosability and Conditional Diagnosability of Strong Networks［J］．IEEE Transactions on Computers，2014，63（7）：881－885．

［5］HSU HC，WU KS，LIN CK，et al．A Linear Time Pessimistic Diagnosis Algorithm for Hypermesh Multiprocessor Systems under the PMC M odel［J］．IEEE Transactions on Computers，2014，63（12）：2894－2904．

［6］洪月华．基于粗糙k－均值的分布式聚类算法［J］．广西科技大学学报，2013，24（1）：89－93．

［7］陈伟，孔峰，陶金．神经网络在网络检测中的应用［J］．广西科技大学学报，2011，22（1）：78－81．

［8］MAENG J，MALEK M．A Comparison Connection Assignment for Self－Diagnosis of Multiprocessor Systems［J］．Symposium on Fault Tolerant Computing，1981，30：173－175．

［9］SENGUPTA A，DANBURA AT．On Self－Diagnosable Multiprocessor Systems：Diagnosis by the Comparison Approach［J］．IEEE Trans actions on Computers，1992，41（11）：1386－1396．

［10］YELC，LIANG JR，LIN HX．A Fast Pessimistic Diagnosis Algorithm for Hypercube－Like Networks under the Comparison Model［J］．IEEE Transactions on Computers，2016：2884-2888．

［11］CHEN CA，CHANG GY，HSIEH SY．Conditional（t，k）－Diagnosis in Graphs by U sing the Comparison Diagnosis Model［J］．IEEE Trans actions on Computers，2015，64（6）：1622－1632．

［12］YE TL，HSIEH SY．A Scalable Comparison－Based Diagnosis Algorithm for Hypercube－Like Networks［J］．IEEE Trans actions on Reliability，2013，62（4）：789－799．

［13］DAHBURA AT，MASSON GM．An O（N2．5）Fault Identication Algorithm for Diagnosable Systems［J］．IEEE Trans actions on Com-puters，1984，33（6）：486－492．

［14］KAMEDA L，TOIDA S，ALLAN F J．A Diagnosing Algorithm for Networks［J］．Information and Control，1975，29（2）：141－148．

［15］SULLIVAN GF．A O（t3＋｜E｜）Fault Identication Algorithm for Diagnosable Systems［J］．IEEE Transactions on Computers，1988，37（4）：388－397．

［16］YANG X，TANG Y．Efficient Fault Identication of Diagnosable Systems under the Comparison Model［J］．IEEE Trans actions on Computers，2007，56（12）：1612－1618．

（学科编辑：黎娅）

A new algorithm of system level fault diagnosis based on extended star structure

ZHOU Ning，LIANG Jia－rong*
（School of Computer and Electronic Information，Guangxi University，Nanning530004，China）

Abstarct：Level fault diagnosis is a kind of important fault diagnosis in network system.By analyzing the property of t-fault conditional diagnosis of PMC fault model and MM fault model,we structure an extended star structure in a defined network topology and use the graph theory to analyze and demonstrate the symptoms of a given PMC model and MM model,then identify the state of the root node of the extended star structure.In the end,we propose a new system level fault diagnosis called extended star structure algorithm for the multi processor network system with extended star structure and certain diagnosis.The theoretical demonstration and experimental results show that this algorithm can easily,fast and correctly identify all faulty nodes in the multiprocessor network system,whose time complexity of the algorithm is O(N),where N is the number of the all nodes of the network.

system-level diagnosis;PMC model;MM model;extended star structure;multiprocessor network system

TP301

A

2095-7335（2016）04-0038-07

10.16375/j.cnki.cn45-1395/t.2016.04.008

2016－05－20

国家自然科学基金项目（61363002）资助．

梁家荣，教授，博士生导师，研究方向：互连网络的故障诊断理论与应用，E－mail：liangjr＠gxu．edu．cn．