基于闭环P型学习控制的线性分布参数切换系统故障诊断

戴喜生，张建香，袁海英，黄庆南

（1．山东科技大学电气与自动化学院，山东青岛266590；2．广西科技大学电气与信息工程学院，广西柳州545006；3．智能综合自动化高校重点实验室（桂林电子科技大学），广西桂林541004）

基于闭环P型学习控制的线性分布参数切换系统故障诊断

戴喜生1，2，3，张建香2，袁海英2，黄庆南2

（1．山东科技大学电气与自动化学院，山东青岛266590；2．广西科技大学电气与信息工程学院，广西柳州545006；3．智能综合自动化高校重点实验室（桂林电子科技大学），广西桂林541004）

研究了一类具有切换模态的线性分布参数系统的故障诊断问题.在实际运行的动态线性分布参数切换系统的基础上，设计了与之对应的虚拟故障跟踪器，通过引入残差信号，建立了闭环P型迭代学习故障跟踪算法；给出了该算法的收敛性充分条件，并通过严格的理论分析，保证了残差信号和故障偏差的一致收敛性；最后通过数值仿真结果进一步验证了所提算法的有效性.

迭代学习控制；分布参数系统；切换；收敛性；故障诊断

0　引言

高度复杂化、智能化是目前工业过程的发展趋势，与此相适应的，控制系统和生产过程设备也越来越复杂、精细.这使得工业生产过程发生故障的机率也加大，研究如何使得这些复杂系统具有更高的安全性和可靠性具有重要意义.近年来，故障诊断技术已成为控制领域里的研究热点之一，目前已经取得了丰富的研究成果［1－2］.

迭代学习控制（Iterative Learning Control，ILC）是一种模仿人类具有学习能力的先进智能控制方法［3］，它基于系统历史的输入和误差信号来调节当前的输入，通过迭代使得系统的输出完全跟踪期望输出.这使得ILC至少具有两个方面的特点：一是ILC控制器结构简单，对给定的期望输出，仅仅需要存储系统以前的输入信号和误差信号即可设计适当的控制器；二是可实现有限时间区间上的完全跟踪；因此，在一些传统PID控制难以满足要求的场合，如高精度运动控制、机器人控制等场合得到广泛应用［4-6］.

将迭代学习控制与故障诊断相结合是学习控制应用的一个重要方面.文献［7］较早给出了一种基于迭代学习的故障诊断与估计算法，其基本思想是利用虚拟的故障跟踪估计器的输出和系统实际输出比较形成残差信号，将残差信号通过迭代学习算法对引入的虚拟故障逐次修正，使虚拟故障逼近系统中实际发生的故障，从而达到对系统故障诊断的目的.利用这种方法，文献［8］讨论了一类具有任意切换规则的离散切换系统的故障诊断问题，文献［9］从学习律速度考虑，设计了一种带有角度修正的迭代学习控制故障诊断方法，一些其他文献也采用学习控制方法研究故障诊断问题，如文献［10］等.

本文利用闭环迭代学习控制算法对一类含有故障的分布参数切换系统进行研究，设计虚拟故障估计器，构造闭环P型迭代学习控制算法，使得故障偏差和残差信号在选择合适的增益矩阵条件下可一致收敛到0，从而实现故障的精确估计.与其他方法相比，特点在于：1）首次利用学习控制方法对分布参数切换系统的故障进行研究.目前已有的分布参数系统故障诊断或估计方法主要有两种，一是采用有限维逼近无穷维的离散化方法，二是李雅普诺夫方法；2）闭环学习控制律由于利用了当前的残差信号，使得学习过程具有更好的抗干扰性和更快的速度［11］；在仿真中对比了开环学习控制算法，结果表明了这一特点.

1　问题描述

有故障的分布参数切换系统：

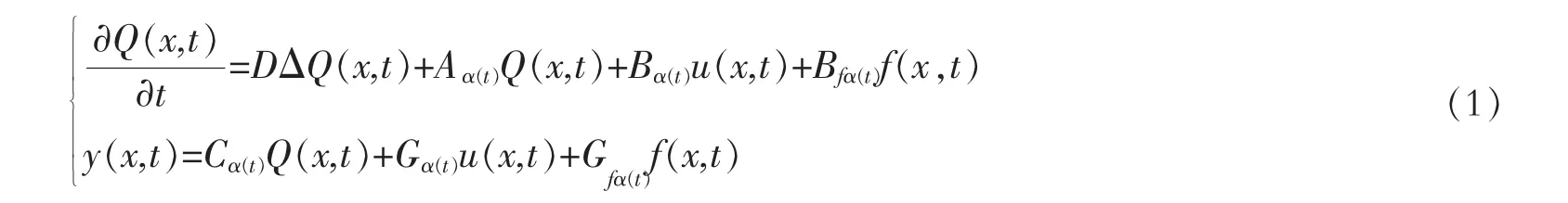
其中，（x,t）∈Ω×［0,T］，Q∈Rn，u∈Rm，y∈Rw分别表示系统状态，输入和输出.矩阵Aα（t）∈Rn×n，Bα（t），Bfα（t）∈Rn×m，Cα（t），Gα（t），Gfα（t）∈Rw×n.D为正的有界对角矩阵，即D=diag［d1,d2,…,dn］，0＜pi≤di＜∞，pi为已知的.Δ是区域Ω上的Laplace算子而Ω是Rq中有光滑边界∂Ω的有界开子集.α（t）是切换规则函数，即α（t）∶［0,T］→I，I=［1,2,…,l］，l为有限正整数.如果切换规则α（t）确定，那么Aα（t），Bα（t），Bfα（t），Cα（t），Gα（t）和Gfα（t）均为确定的相应维数常数矩阵，f（x,t）∈Rm为系统的故障信号.

分布参数切换系统（1）的初边界条件如下，对每一个切换模态都有：

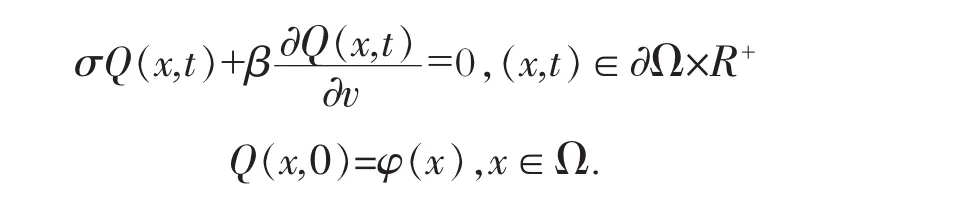
本文的目的是要当系统发生故障时估计故障f（x,t）的大小，为此首先设计如下的虚拟故障跟踪估计器：

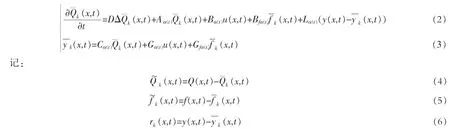
然后，为使得虚拟故障逼近（迭代）实际故障，基于残差信号rk（x,t）给出如下的闭环P型迭代学习控制算法：

式（2）～式（8）中，k为迭代次数；Q¯k（x,t）为系统状态的估计值为系统输出的估计值；rk（x,t）为残差信号；Lα（t）是预先给定的增益矩阵；Γ为学习增益矩阵.

基于文献［10］，本文的估计故障基本思想如下：在选取的优化时域内，利用系统（1）实际输出y（x,t）和故障跟踪估计器输出向量的残差信号rk（x,t），通过迭代学习方法（7）调节引入的虚拟故障，来逐次逼近系统的真实故障，从而达到对故障估计的目的；同时从理论上证明所给算法可以使得虚拟故障逼近实际故障f（x,t），且逼近过程是关于时间一致收敛的.式（8）表示在实际系统输出和估计器输出满足该式时，故障估计器停止对虚拟故障进行修正，ε是给定的性能指标.

假设在学习过程中，系统（2）和系统（3）的初边界条件始终满足：

由文献［12］可知，若是系统（1）具有多个切换子系统，本文后面的证明过程与系统具有2个子系统是类似的.

以下引理将在算法收敛分析中用到.

引理1［3］设非负实序列｛ak｝与｛εk｝满足不等式ak+1≤ρak+εk，其中0＜ρ＜1，则当limεk＝0时，有lim ak＝0.

引理2［13］设f（t）,g（t）在有限时间区间［0，T］上为非负连续函数，而且存在非负常数q,M，使得不等∫t

∫t式f（t）≤q+g（t）+M0f（s）d s成立，则可知不等式f（t）≤q eMt+g（t）+M eMt0g（s）e-Msd s成立.

引理3［13］设常数序列｛b｝收敛到0，序列｛Z（t）｝⊂C［0,T］满足：

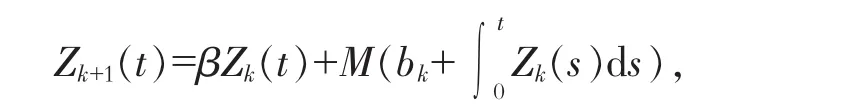
则当k→+∞时，序列Zk（t｛｝）k≥0一致收敛到0.其中，M＞0,0＜β＜1均为常数.

2　闭环P型迭代学习控制算法的收敛性分析

定理1针对满足假设条件的分布参数切换系统，利用所设计的故障估计器，对该系统所发生的故障基于闭环P型迭代学习算法进行估计时，如果学习过程中初边值条件分别为式（9），式（10），且学习增益矩阵满足：

即虚拟故障估计器的故障逼近实际系统故障，达到故障估计目的.

证明：由式（6）和式（7）可得：

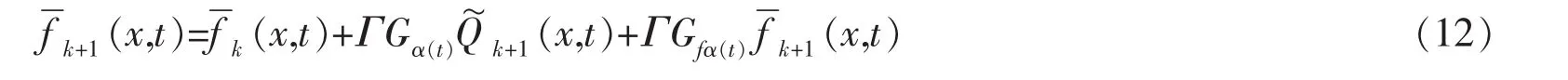
由式（3）和式（5）可得：

即故障估计器的输出逼近实际输出.

证明：由表达式（6），式（19）以及定理1的结论容易得到式（31），详细证明省略.

3　数值仿真

考虑如下具有2个子系统并带有故障的线性分布参数切换系统，其中D=1，切换规则α（t）=1或者2，x×t∈［0，1］×［0，0.8］：

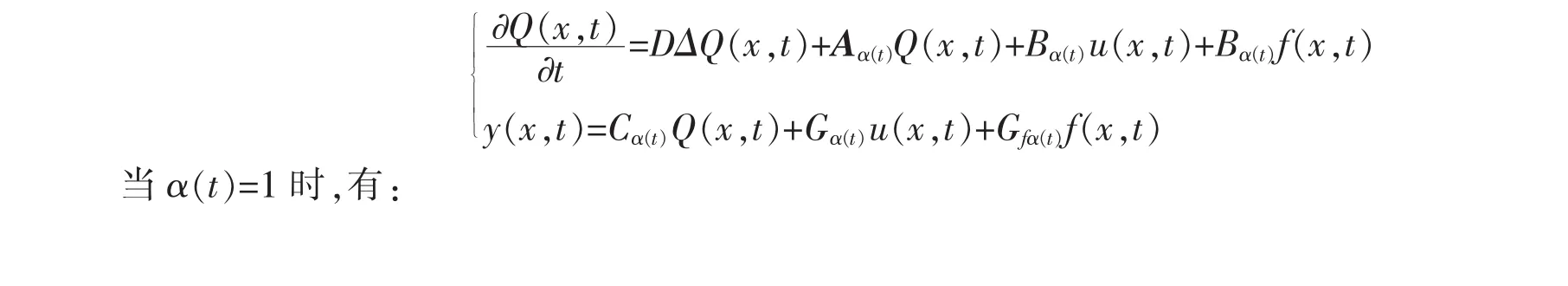
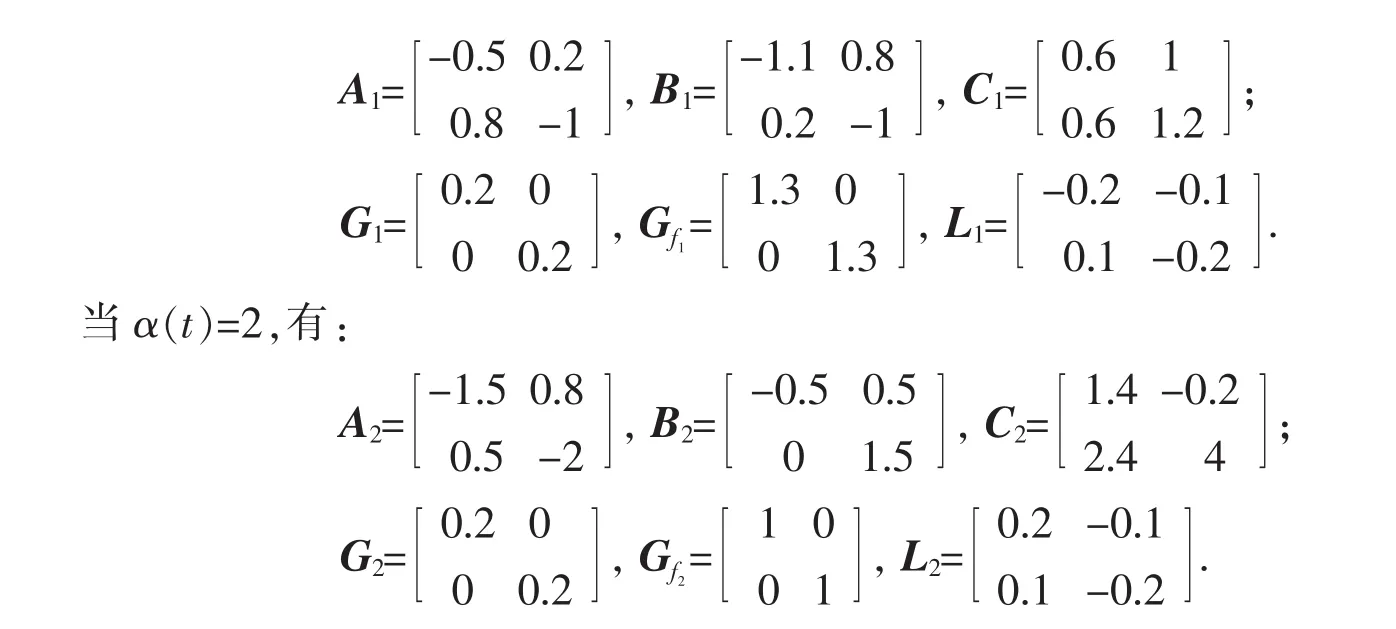
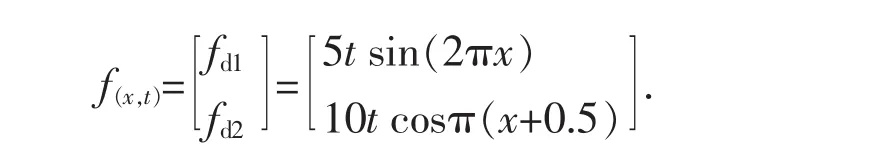
利用偏微分方程的差分计算方法，并结合本文的迭代学习控制算法，仿真结果如图1～图6所示.图1和图2为系统实际发生的故障；图3和图4为迭代15次后故障估计器的故障；图5～图6分别是闭环P型学习律故障误差和输出偏差随迭代次数变化图；为和开环算法比较，图7～图8为当系统采用开环P型迭代学习算法时获得的对应的故障偏差和输出误差随迭代次数变化曲线.

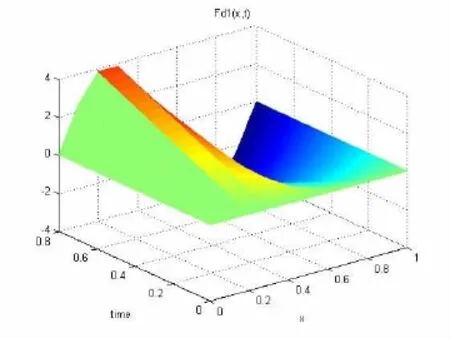
图1　系统实际故障fd1Fig．1 Actual fault of system fd1

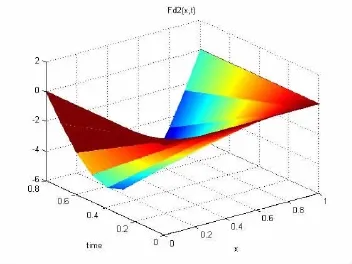
图2　系统实际故障fd2Fig．2 Actual fault of system fd2

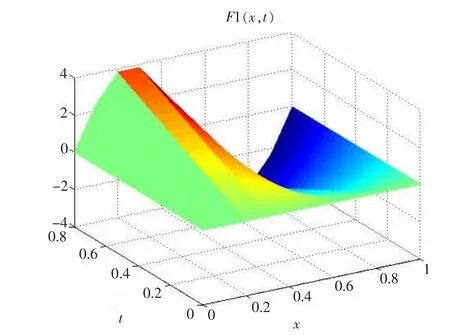
图3　估计器的故障估计f1Fig．3 Fault estimation of the estimator f1

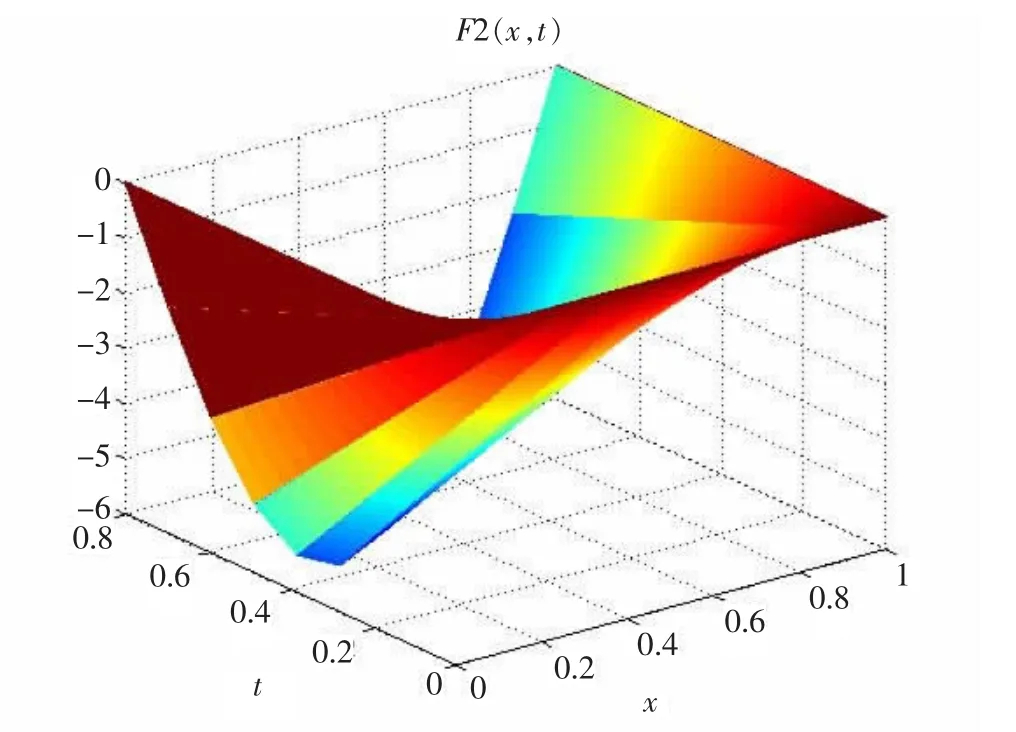
图4　估计器的故障估计f2Fig．4 Fault estimation of the estimator f2

由图3～图4可知，当迭代次数达到15次时，故障估计器的故障趋近于系统的实际故障；从图5和图6可知，随迭代次数增加，故障估计器的故障逐步逼近实际故障，且输出也趋于实际输出；而从图5～图8可知，闭环学习律要稍优于开环学习律，数值上，当迭代10次时，闭环故障偏差为2．592×10－4，3．977 9×10－4，输出误差为1．959×10－4，4．141×10－4，而开环故障偏差为1．854×10－2，2．137×10－2，输出误差为1．351×10－2，2．776×10－2.

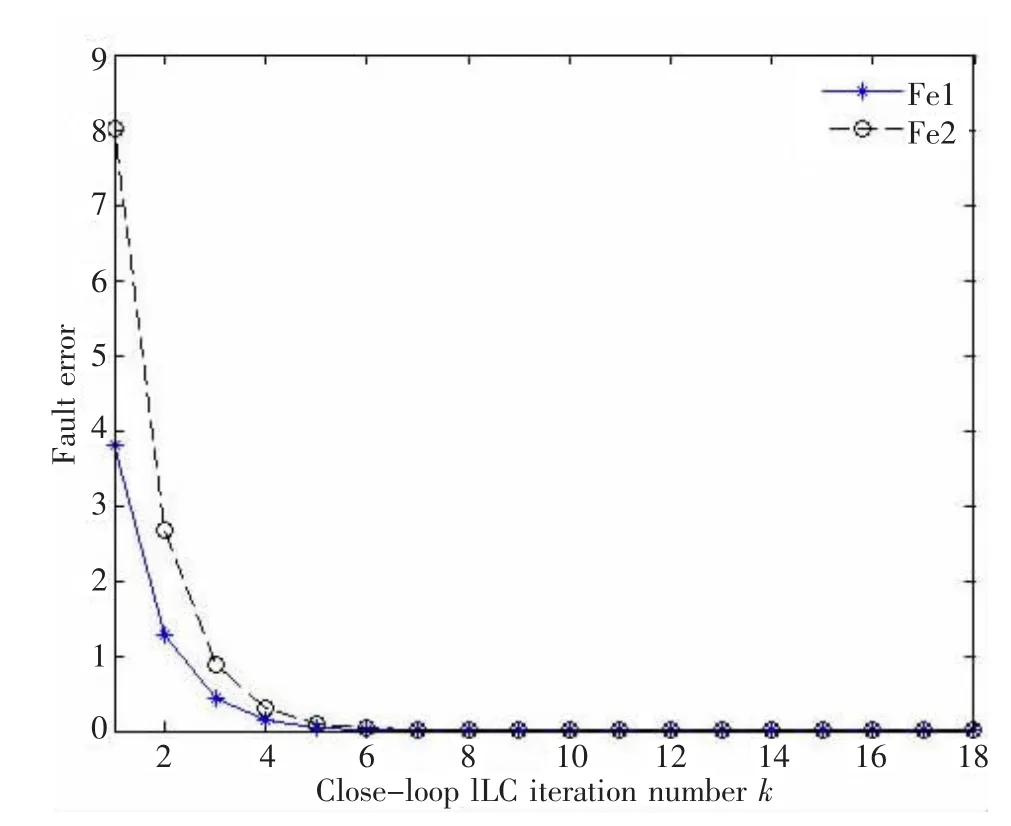
图5　闭环学习故障偏差-迭代次数曲线Fig.5 The closed-loop learning curve of fault error-iterative number

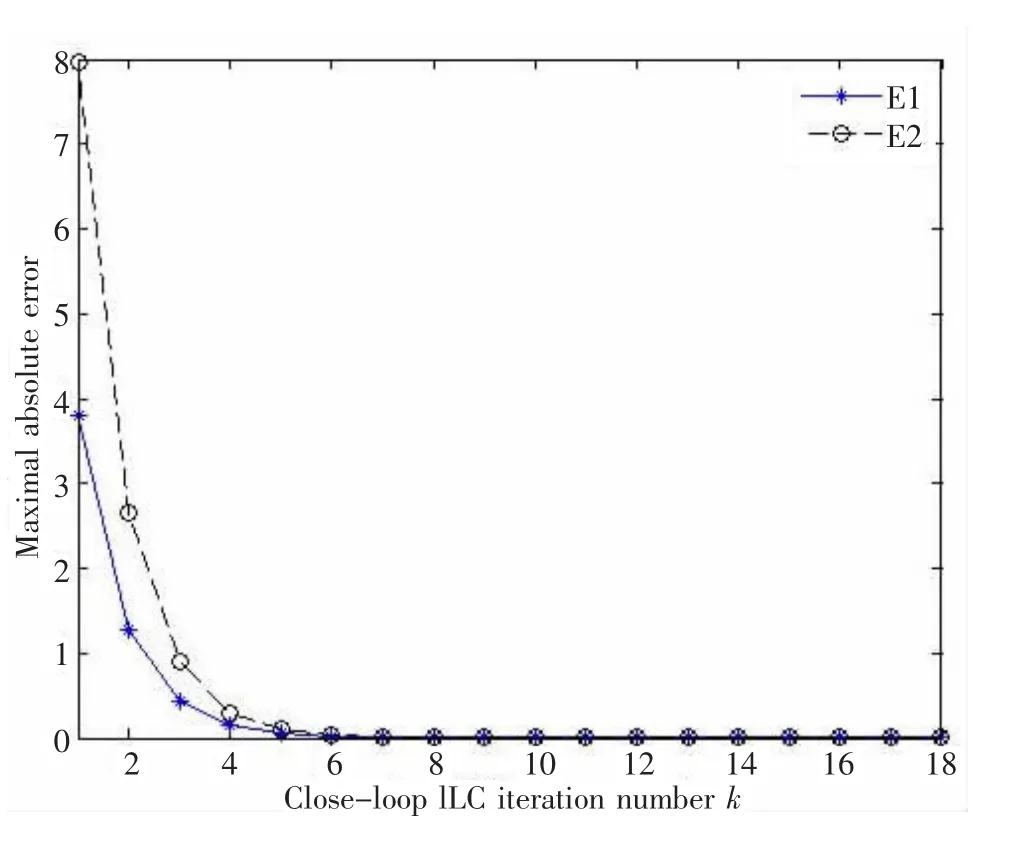
图6　闭环学习输出误差-迭代次数曲线Fig.6 The closed-loop learning curve of output error-iterative number

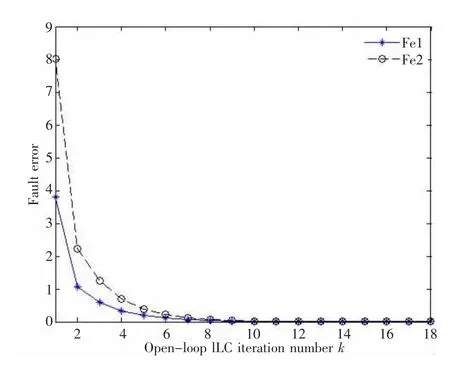
图7　开环学习故障偏差-迭代次数曲线Fig.7 The open learning curve of fault error-iterative number

图8　开环学习输出误差-迭代次数曲线Fig.8 The open learning curve of output error-iterative number

本文对一类线性分布参数系统切换的故障诊断问题进行了研究.设计了故障估计器，建立了基于闭环学习律的故障逼近算法，给出了算法收敛的充分条件，仿真结果表明了所给算法的有效性.

［1］X U A，Z HANG Q．Nonlinear System Fault Diagnosis Based on Adaptive Estimation［J］．Automatica，2004，40（7）：1181－1193．

［2］周东华，孙优贤.控制系统的故障检测与诊断技术［M］，北京：清华大学出版社，1994．

［3］孙明轩，黄宝健．迭代学习控制［M］．北京：国防工业出版社．1999．

［4］CUI J，ZHAO F，CHU Z Y，et al.Experiment on Trajectory Tracking Control of High Precise Positioning System Based on Iterative L earning Controller with Wavelet Filtering［J］．Mechatronics，2015，32：88－95．

［5］F REE CT.Newton－Method Based Iterative L earning Control for Robot－Assisted Rehabilitation Using FES［J］.Mechatronics，2014，24（8）：934–943．

［6］谢胜利，田森平，谢振东．迭代学习控制的理论与应用［M］．北京：科学出版社，2005.

［7］高林，刘喜梅，顾幸生．一种新的基于迭代学习的故障检测和估计算法［J］．控制与决策，2010，25（8）：1173－1177.

［8］曹伟，郭媛，孙明．基于迭代学习的离散切换系统的故障估计［J］．物理学报，2014，63（18）：180－202．

［9］曹伟，孙明．基于角度修正迭代学习的离散时变系统故障诊断［J］．控制理论与应用，2012，29（11）：1495－1500．

［10］陶洪峰，陈大朋，杨慧中．基于扩展滤波器的非线性系统迭代学习故障诊断算法［J］．控制与决策，2015（6）：1027－1032．

［11］曾南，应行仁．非线性系统迭代学习算法［J］．自动化学报，1992，18（2）：168－176.

［12］BU X H，Y U F S，HOU Z S，et al．Iterative Learning Control for a Class of Non－Linear Switched Systems［J］．IET Control Theory and Applications，2013，3（7）：470－481．

［13］林辉，王林．迭代学习控制理论［M］．西安：西北工业大学出版社，1998．

［14］戴喜生，罗文广，曹立生，等．初值大偏差分布参数系统迭代学习跟踪控制［J］.广西科技大学学报，2012，23（4）：18－22．

（学科编辑：黎娅）

Fault diagnosis for linear distributed parameter switched system based on closed-loop P-type iterative learning control

DAI Xi－sheng1，2，3，ZHANG Jian-xiang2，YUAN Hai－ying2，HUANG Qing－nan2
（1.School of Electrical Engineering and Automation,Shandong University of Science and Technology,Qingdao 266590,China;2.School of Electrical and Information Engineering，Guangxi University of Science and Technology,Liuzhou 545006,China;3.Colleges and Universities Key Laboratory of Intelligent Integrated Automation(Guilin University of Electronic Technology),Guilin 541004,China）

This paper studies the problem of fault diagnosis for linear distributed parameter switched systems.A virtual fault tracking estimator is proposed based on actual linear distributed parameter systems with switched modal.The closed-loop P-type iterative learning algorithm is established by introducing residual signal.The sufficient conditions that guaranteed the uniform convergence of residual signal and fault error are derived through rigorous analysis.In the end,an illustrative example is presented to demonstrate the performance of the proposed ILC algorithm.

iterative learning control;distributed parameter system;switch;convergence;fault diagnosis

TP273

A

2095-7335（2016）04-0007-08

10.16375/j.cnki.cn45-1395/t.2016.04.002

2016－06－30

国家自然科学基金项目（NSFC61364006）；广西高等学校优秀中青年骨干教师培养工程(桂教人[2014]39号)；智能综合自动化高校重点实验室基金（智字201502）；广西教育厅科研项目（KY2016YB248）资助．

戴喜生，博士(后)，副教授，研究方向：分布参数系统迭代学习控制，随机系统稳定性分析，E-mail：mathdxs＠163．com．