桥体索鞍的有限元分析

王虎奇，尹玉鹏，潘芳秦

（广西科技大学机械工程学院，广西柳州545006）

桥体索鞍的有限元分析

王虎奇，尹玉鹏，潘芳秦

（广西科技大学机械工程学院，广西柳州545006）

以某大桥为工程背景，对主桥桥体索鞍进行分析研究．首先使用有限元分析软件ANSYS建立鞍体有限元模型，然后对鞍体模型进行了静态分析、优化设计、模态分析和屈曲分析，最后得到鞍体的结构变形、应力分布规律和结构最优设计方案，以及鞍体结构的谐振频率和失稳临界载荷、屈曲模态.通过ANSYS软件的仿真分析获得的结果为鞍体结构设计改进提供了理论依据，可以有效地预先避免鞍体设计时发生共振、鞍体塑性变形及鞍体断裂等现象，同时为同类工程问题提供了有价值的参考方案．

有限元分析；静态分析；优化设计；模态分析；屈曲分析

0　引言

现代一些桥梁经常会出现主桥跨中下挠和箱梁腹板开裂等问题，针对这一系列问题的产生，桥梁管理部门对某桥梁主桥箱梁的裂缝和桥面的线形进行了观察和监测．经过对大桥多年的观查和监测，主桥箱梁腹板的开裂和跨中下挠等桥梁问题持续恶化．为解决该桥梁主桥箱梁腹板开裂和跨中持续下挠的难题，桥梁管理部门对该主桥进行了斜拉体系改造；主塔处设置滑动索鞍，通过索鞍滑动消除温度影响下的桥塔根部弯矩．为确保索鞍的滑动可靠性，需要进行索鞍的实体滑动试验．本文运用ANSYS软件对鞍体建立有限元模型，对鞍体结构进行静力分析，在其基础上对鞍体的加强筋厚度做优化处理，并在鞍体滑动试验的基础上对鞍体进行模态分析和屈曲分析．以确定索鞍是否能够正常有效的工作．

1　鞍体有限元模型的建立

1．1鞍体有限元模型的建立

建立边塔索鞍鞍体的有限元模型是对鞍体进行有限元分析时最为关键的一步，实体有限元模型的质量直接影响最终分析结果的准确性［1］．本次有限元模型的建立采用自顶向下和自底向上相结合的建模方法．鞍体建模时，要考虑鞍体节构的复杂程度．建立较为准确的鞍体几何模型并不能保证分析计算的绝对准确性，有时过于精确复杂的曲面网格划分后会出现畸变单元，从而得不到符合实际的分析结果．故在建立鞍体有限元模型时，为了精确地进行有限元分析，要对模型进行简化处理［2］．在不影响分析结果的前提下做出以下几点简化：

1）由于鞍体的底部与耐磨板是通过六角螺栓进行镶嵌的，为了减少计算量，可以将螺栓孔省略；

2）为了提高网格划分的质量，在减少计算量的前提下提高计算效率，可以将某些对鞍体分析结果没有影响的吊装孔等忽略；

3）省去工艺结构和本次实验分析非感兴趣的区域．

鞍体的铸造材料为ZG310－570，泊松比μ为0．3，弹性模量E为2．02G P a，体积质量ρ为7 800 kg／m3．通过单元类型的对比，最终鞍体有限元模型的单元类型选为Solid187 3－D 10节点四面体单元．利用ANSYS建立的有限元模型如图1所示．

图1　鞍体的有限元模型Fig．1 The finite element model of saddle

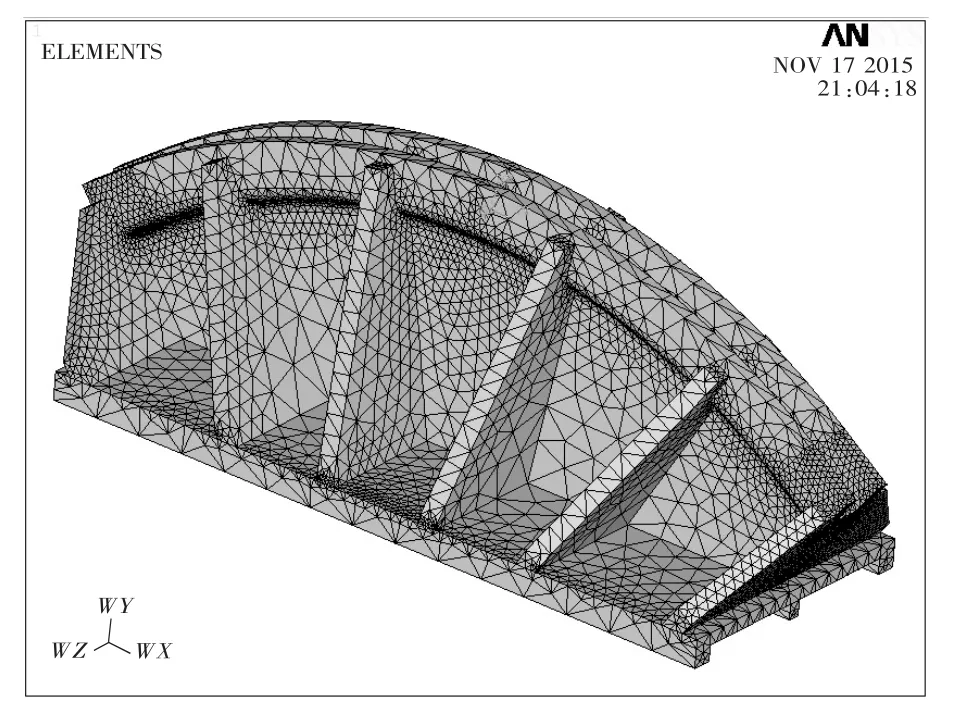
图2　鞍体的网格划分模型Fig．2 The mesh generation model of saddle

1．2鞍体有限元模型的网格划分

网格划分是有限元分析中的关键工作，网格划分的质量优劣将对计算结果产生相当大的影响［3］．自由网格划分对有限元模型的形状没有很高的要求，对不规则几何模型也可以进行网格划分．本文鞍体的有限元模型采用的就是自由网格划分方法．图2为鞍体的网格划分模型．该模型共包括96 823个单元．

2　鞍体的结构静力分析

2．1等效索力计算

令索鞍索槽的法向压力为q，索鞍索槽法向应力分布做纵向平面受力分析［4］．索鞍索槽法向应力分布如图3所示（θ1=54.3°）．

取一法向力为qR dθ的微元体，其竖直方向的分力为qRdθsinθ，由Y方向受力平衡可得：Σy＝0

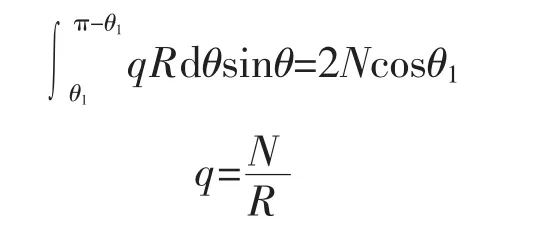
本文中N取实验拉索力最大值450 T，R取2m．将其代入公式可得q＝2．25×106N．

由索槽弧长（L）公式、索鞍索槽底面面积（A）公式及应力公式：

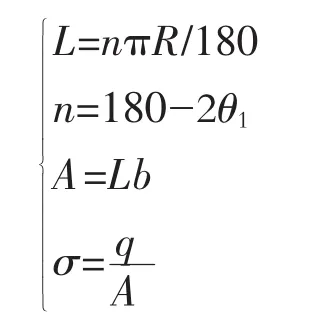
可得鞍体索槽底面所受面载荷σ＝9．31×106P a．

2．2对模型定义边界条件并求解

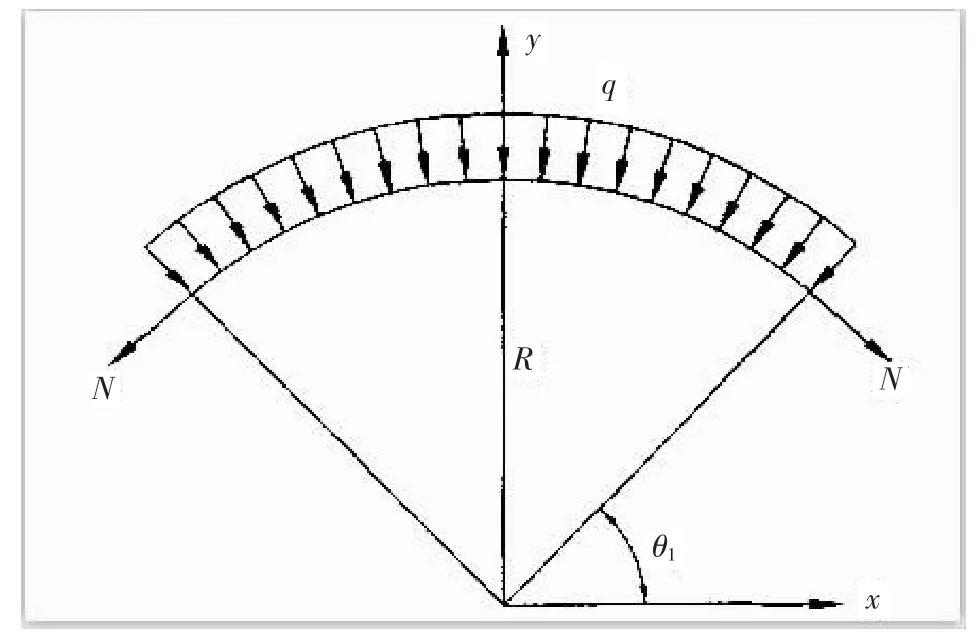
图3　索鞍索槽法向应力分布Fig．3 The s tress distribution in the normal direction of the c able s addle

在鞍体模型底面对位移边界进行全约束，在鞍体的索槽底面施加面载荷σ．图4为鞍体有限元模型载荷．

对鞍体进行求解，查看鞍体试驾载荷后的变形情况，图5为鞍体的变形图，图中无色网格区域为鞍体未变形前的形状，蓝色区域为鞍体变形后的形状．

由鞍体求解结果中的应力云图和总位移变形图可知：鞍体的最小应力点发生在鞍体底座，为3 962．07P a；最大应力点位于80°加强筋与鞍体内侧连接附近的弧顶周围，为35．2M P a（鞍体的危险点）；最大位移变形量处于索槽弧顶处，大小为0．035 8m．故可得鞍体的薄弱位置处于鞍体的80°加强筋与弧形索槽连接的附近．图6为鞍体的应力云图．

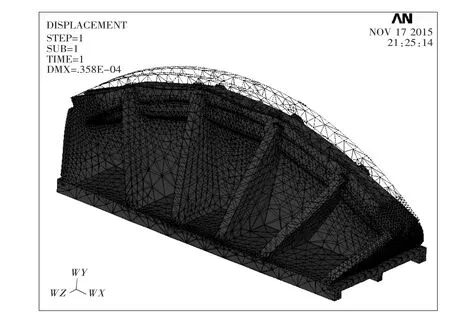
图5　鞍体变形图Fig．5 The deformation diagram of saddle

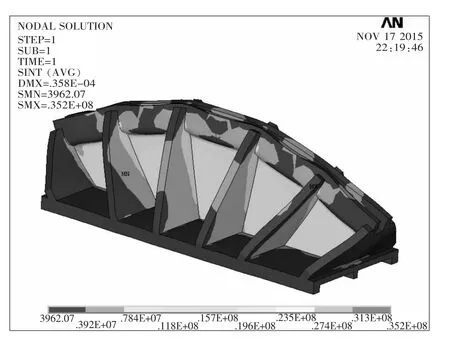
图6　鞍体的应力云图Fig．6 The s tress nephogram and total displacement deformation of saddle

3　鞍体的优化

3．1鞍体优化的参数设定

所谓的结构优化是指设计者遵循设计要求，在满足各种特定条件和限制要求的前提下，应用数学方法使重量、频率、刚度等广义性能达到最优［5］．结构优化设计主要包括2个方面的主要内容：一是将实际工程问题抽象化为优化设计的数学模型，二是应用最优化数值方法求解所建立的数学模型［6］．数学模型建立后，优化问题就变成了纯粹的数学问题．在模型建立后选择适当的优化方法便可对其进行优化．定义加强筋厚度为B，索鞍底面凹槽高度为H，且B＝0．06m，H＝0．05m．

令B，H设为设计变量，鞍体材料的最大屈服强度SMAX设为状态变量，为了减轻鞍体重量实现轻量化，设鞍体总体积V为目标函数，采用零阶法优化．得到图7所示的优化结果．

3．2鞍体的优化的结果及验证

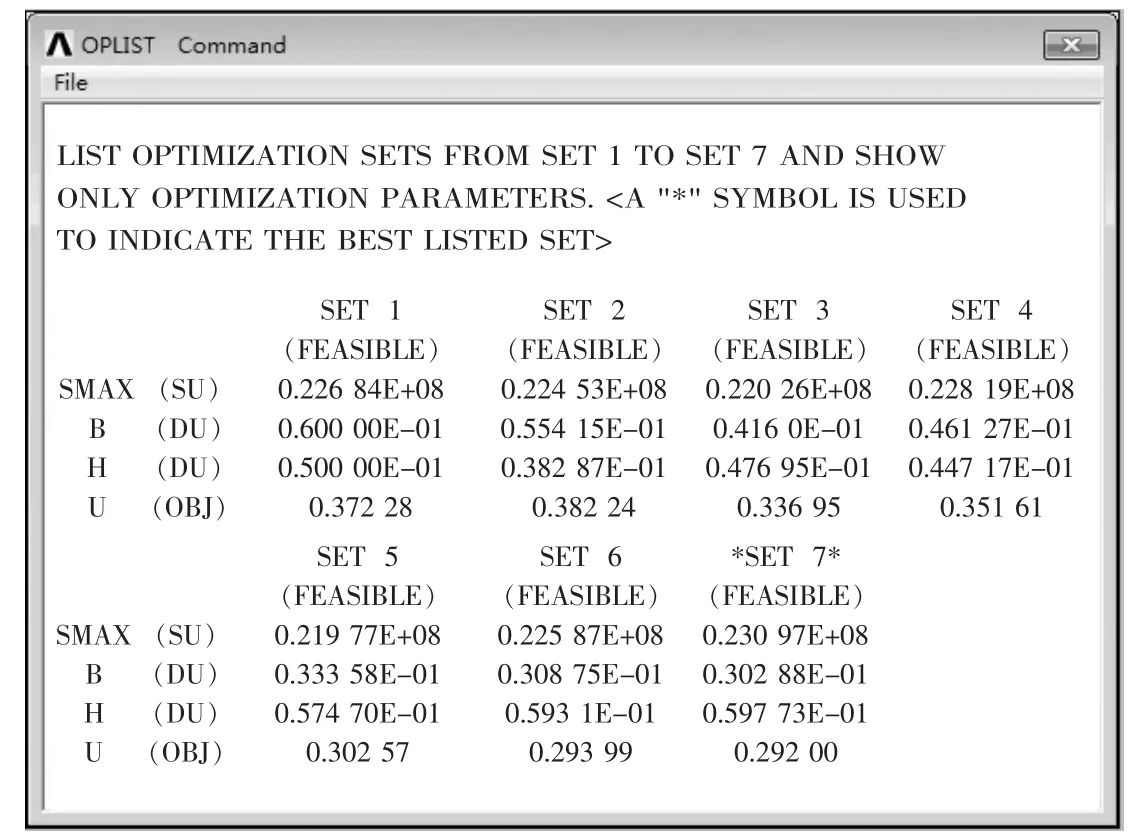
图7　鞍体的优化结果Fig．7 The optimization results of saddle

鞍体的制作工艺一般采用铸造的方法，铸造鞍体时，为了铸造方便，通常对鞍体的参数取整，于是可得到最优结果为B＝0．03m和H＝0．06m．再次对鞍体进行新的尺寸建模并对其做结构静力分析，验证优化结果的合理性．由新数据建模后静力分析的应力云图和总位移变形图与原静力分析结果对比可知：优化后的鞍体最大应力点（危险点）位于加强筋与索槽相交54.3°的底部附近，大小为34.9M P a，比优化前减小了0.3M P a.最大位移变形为0.040 5m，比优化前增加0.004 7m，变形几乎不明显，对鞍体的使用性能没有较明显的影响，故得到的最优解是一个合理的优化结果，可以采用.图8（a）为优化后鞍体静力分析的应力云图，图8（b）为总位移变形图.

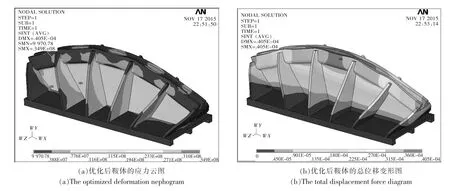
图8　优化后的应力云图及总位移变形图Fig．8 The optimized deformation nephogram and total displacement f orce diagram

4　鞍体的模态分析

4．1鞍体的模态分析

模态分析是一种既可以确定结构固有频率和振动特性，又可以避免机构发生共振现象或使机构进行特定频率振动的新型技术，采用理论与试验相结合的方法来解决各种振动问题，是处理结构动力学问题的支柱［7］.模态分析一般需要建模、加载、求解、扩展模态、查看结果、后处理等分析过程.模态分析中所需的模型只对线性有效，指定的非线性单元系统会忽略并自动默认为线性［8］.

4．2鞍体模态分析的方法及结果

本次鞍体模态分析的分析方法选为Block Lanczos分析方法，频率范围为0到100 000 H z，并进行前十阶模态分析阵型的提取.求解后的模型前十阶频率列表如图9所示.

鞍体模态计算结果的各振型图如图10～图14所示.

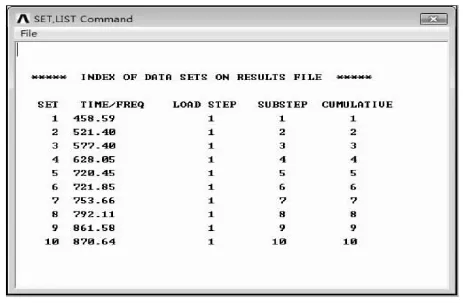
图9　模型前十阶频率表Fig．9 The top ten frequency table of the model

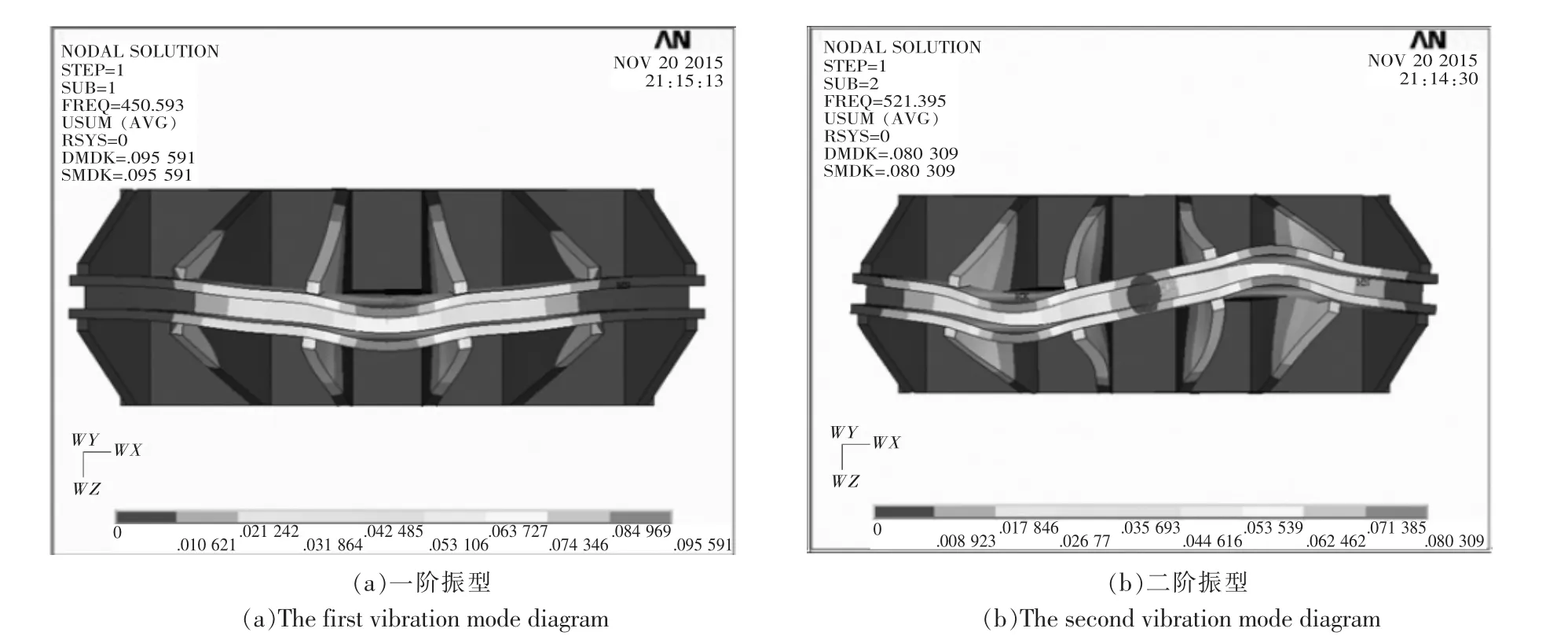
图10　一阶、二阶振型Fig．10 The first and second vibration mode diagram

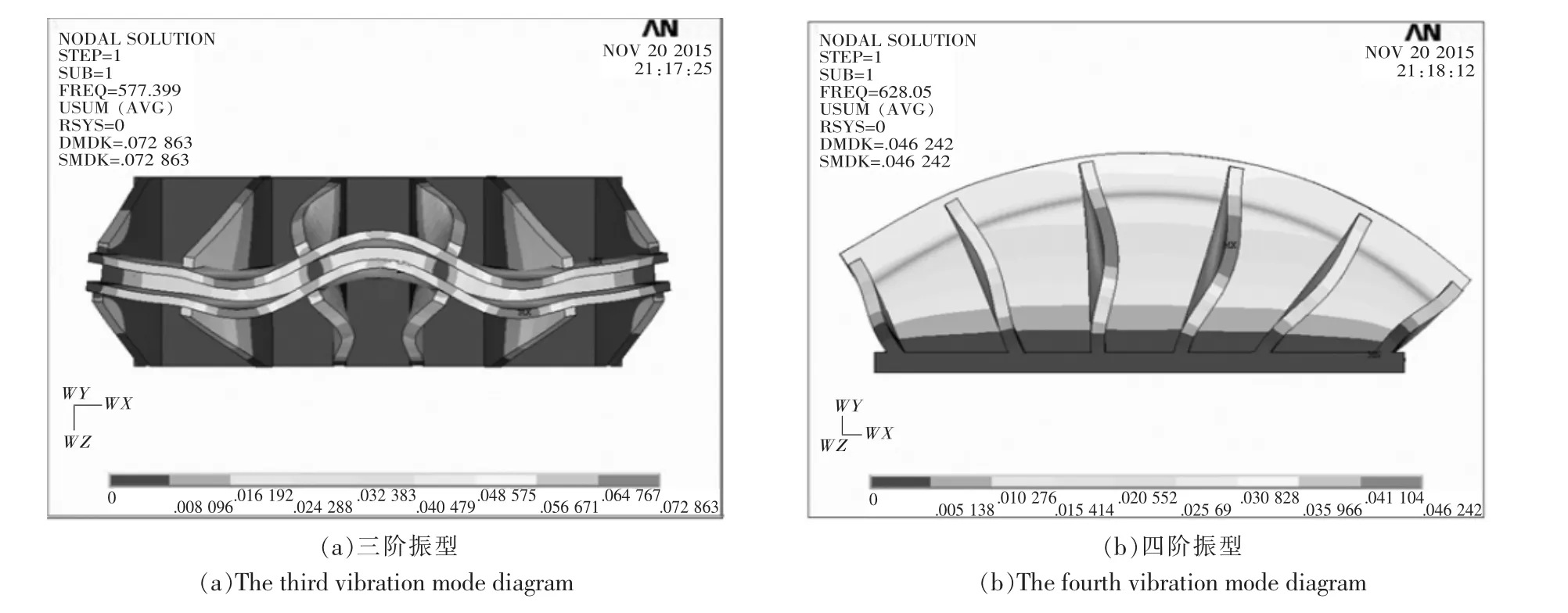
图11　三阶、四阶振型Fig．11 The third and fourth vibration mode diagram

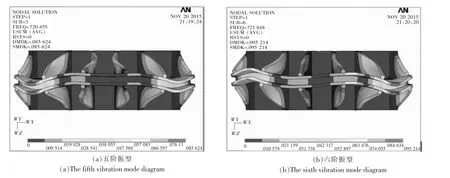
图12　五阶、六阶振型Fig．12 The fifth and sixth vibration mode diagram

图13　七阶、八阶振型Fig．13 The seventh and eighth vibration mode diagram

图14　九阶、十阶振型Fig．14 The ninth and tenth vibration mode diagram

4．3鞍体十阶振型图的分析

由模态分析结果可知：

一阶振型弧形索槽弹性变形不大，加强筋无明显变形．

二阶振型弧形索槽有明显变形，但加强筋变形不大．

三阶振型、五阶振型、六阶振型和八阶振型，弧形和加强筋都有较明显的变形．

四阶振型弧形索槽和加强筋无明显变形．

七阶振型弧形索槽有轻微变形，80°加强筋有明显变形．

九阶振型弧形索槽无变形，80°加强筋有明显变形．

十阶振型弧形索槽有轻微变形，60°加强筋有明显的变形．

通过提取前十阶模态分析的数据，安放索鞍时可以避开桥梁振动幅度大的区域，避免共振现象的发生．

5　鞍体的屈曲分析

屈曲分析是指在失稳时，结构的临界载荷和屈曲模态形状确定的过程．本文中鞍体屈曲分析时模型的建立和求解过程与前文中的静力分析相同，施加在索槽的面应力由σ变为单位面应力．

通过鞍体的屈曲分析，最终可得到鞍体的临界载荷为10 677M P a，总变形位移为0．972 437m．图15为鞍体变形与未变形图及鞍体的屈曲位移变形图．

图15　鞍体的变形图及屈曲位移变形图Fig．15 Figure deformation and buckling deformation displacement of the s addle

6　总结

本文以某大桥为工程背景，通过对桥体索鞍鞍体的有限元分析，可以得知鞍体的应力分布规律、机构优化的最优设计方案、结构刚度和强度的变化以及失稳时的临界载荷，鞍体设计时可以有效避免共振、鞍体塑性变形及鞍体断裂等现象的发生，为实际工程问题的解决提供了可靠的研究数据及一定的理论基础．

［1］王新敏．ANSYS工程结构数值分析［M］．北京：人民交通出版社，2007．

［2］廖金深，沈光烈，林圣存．对某微型客车车身结构的有限元分析［J］．广西科技大学学报，2016，27（1）：58－61．

［3］王国强．实用工程数值模拟技术及其在ANSYS上的实践［M］．西安：西北工业大学出版社，1998．

［4］滕启杰，张哲，余报楚，等．万新大桥梁端滑动索鞍设计与受力分析［J］．武汉理工大学学报（交通科学与工程版），2006，30（1）：154－157．

［5］陈永兵．遗传算法及其在结构工程优化中的应用研究［D］．西安：西北工业大学，2001．

［6］刘齐茂．某型载货车车架结构的优化设计［J］．广西工学院学报，2004，15（4）：8－12．

［7］傅志方，华宏星．模态分析理论与应用［M］．上海：上海交通大学出版社，2000．

［8］李庆龄．5－UPS／PRPU并联机床的动态特性分析［D］．秦皇岛：燕山大学，2006．

（学科编辑：黎娅）

Finite element analysis of the bridge saddles

WANG Hu－qi，YIN Yu－peng，PAN Fang－qin
（School of Mechanical Engineering，Guangxi University of Science and Technology，Liuzhou 545006，China）

According to the conditions of someone bridge,an analysis is studied on the main bridge saddles.The model of the saddles is established on the basis of ANSYS.While the structural deformation,stress distribution, structure vibration frequencies,critical load and buckling mode of the saddles are obtained by carrying out the static analysis,optimum design,modal analysis and buckling analysis of the saddles.It can effectively avoid resonance, plastic deformation and fracture of the saddles.All of what we do can provide the reference theoretical data to improve the stiffness and the overall design of the saddles,meanwhile,provide an effective solution to the practical engineering problem.

finite element analysis;static analysis;optimum design;modal analysis;buckling analysis

TH11；TH164

A

2095-7335（2016）04-0029-07

10.16375/j.cnki.cn45-1395/t.2016.04.006

2016－06－02

国家自然科学基金项目（51565006）资助．

王虎奇，博士，教授，研究方向：工程机械结构系统优化设计，E－mail：809781726＠qq．com．