随机波动率Hull-White模型参数估计方法

江　良,林鸿熙

(1.莆田学院数学学院,福建莆田351100;2.莆田学院商学院,福建莆田351100)

随机波动率Hull-White模型参数估计方法

江良1,林鸿熙2

(1.莆田学院数学学院,福建莆田351100;2.莆田学院商学院,福建莆田351100)

构建随机波动率的两因子模型,应用两阶段半参数方法估计模型中的常系数参数,使用核估计方法估计长期均值函数,给出了两阶段估计方法的相容性和参数的渐近性性质.实证结果表明了对比常系数模型,引入长期均值函数模型将会改善似然函数估计值,而且也能够很好地解释中央银行和政府已实施政策的有效性.此外,可以在不增加维数的条件下,使用该模型对利率衍生品进行更有效地定价.

长期均值;随机波动率;短期利率模型;半参数估计;核估计方法

1　引　言

利率是金融市场中非常重要的一个指标,几乎所有的金融现象和活动都和利率相关.因此构建合适的短期利率模型变得尤为重要.构建短期利率模型可分为两类:单因子模型;多因子模型.虽然实证表明了单因子模型也能很好地拟合市场的数据[1,2],但是单因子模型无法产生较复杂的收益率曲线的形状.因此,多因子短期利率模型应运而生[3,4].

Litterman等[5]基于实证方法论述了随机波动率模型的必要性.Kim等[6]应用多因子模型对日本债券收益率数据进行分析发现当瞬时利率很小时,两因子高斯模型拟合效果较好.Cheridito等[7]和Pierre等[8]基于横截面数据相应给出多因模型的参数估计方法及实证的结果.虽然,上述的研究结果表明了可以通过引入状态变量改善模型的拟合效果,但是相应的衍生品定价的维数也增加从而导致数值方法也变得更加困难,而且相应的参数估计问题也变的困难.如Duffee等[9]指出了由于多因子模型的复杂性,相应的参数估计识别问题也变得困难.因此,为了给出最优的统计方法,选择了状态变量相互独立的仿射性结构模型.

为了给出简约的模型,Andersen等[10],Fong等[11],Longstaff等[12]及Surya[13]构建了随机波动率两因子模型,并通过实证分析说明了引入随机波动率是必要的.然而在上述的模型中,长期均值均是常数.因此,Balduzzi等[14,15],和Chen[16]研究了引入长期均值作为状态变量的短期利率模型,并通过实证和数值分析说明了该模型不仅改变了短期利率期限结构的形状而且也改善了拟合效果.范龙振等[17]在漂移项中引入了储蓄存款利率作为状态变量来改善拟合效果.但是,由于引入新的状态变量,相应的衍生品定价偏微分方程的维数也会增加,从而导致数值方法变得比较复杂.另一方面,在文献[14,15]中,长期均值几乎和瞬时利率呈现一样的震荡,这种现象很难精确地刻画长期预期利率的趋势.江良[18]也通过核估计方法估计了Hull-White模型中的参数,但该作者考虑的模型是单因子模型.

基于上面分析的原因,本文用时间函数描述长期均值的变化,考虑了随机波动率的短期利率模型,并相应地给出了半参数估计方法.该模型既能改善数据的拟合效果也不增加衍生品定价的维数,并兼顾随机波动率良好的特性.而且实证分析也表明了引入均值函数能更好地刻画中央银行和政府已实施政策的有效性(详细的分析见本文第4节).此外,考虑均值函数的模型也可改善衍生品的定价.如Hull等[2]研究了时间变量系数的单因子模型衍生品定价时,他们发现其衍生品的定价和常数系数的两因子模型没有显著的差异. Grzelak等[19]引入Hull-White模型给出债券定价过程,并指出引入Hull-White模型是必要的.

为了说明本文模型的有效性,将使用似然函数来诊断模型.由于模型中含有时间函数的参数,因此将提出一种半参数估计方法来计算似然函数值.根据H¨ardle等[20]和Ramsay等[21]对于半参数模型的估计方法一般可分为如下两类:核估计方法;正则化方法.本文将选择核估计方法,其主要原因是均值函数可通过核函数在每个节点上加权平均近似,其近似的函数仅依赖于给定窗口.此外,由于瞬时波动率是不可观测的,因此将通过两组不同到期日债券的线性组合来近似波动率过程[16,22].本文模型是在风险中性测度下所构建的,这就使得对利率衍生品的定价时可直接使用这些参数的估计值.

2　随机波动率Hull-White短期利率模型

首先,假设在风险中性测度下短期利率满足下面的模型(SVHW)

在该模型中瞬时波动率满足CIR模型[23]以至于使得波动率是非负的(假设Feller条件满足),而且长期波动率是一个常数.一个似乎更合理的假设是式(1)满足CIR随机过程,然而归咎于相关系数ρ,此时债券价格无仿射性结构解[24].但是相关系数又是一个非常重要的指标.如,Balduzzi等[15]发现了利率和随机波动率水平变化是正相关的.Cheridito等[7]通过债券数据发现了相关系数也是正的(几乎接近1).基于这些原因,不考虑对于随机利率满足CIR动态过程的模型.

注意到,SVHW模型包含一些其它的模型.当波动率是常数时,就是众所周知的HW模型[2];当θ(t)是常数时,模型变化为FV模型[11];当波动率Vt和θ(t)都是常数时,其模型为Vasicek模型[25].

根据计价单位转换原理[24],如果选取银行账户作为计价单位,则是一个鞅,其微分为

根据鞅的性质,可得以下偏微分方程.

其终端条件为P(T,T)=1.

根据Duffie等[4]研究的结果,方程式(3)存在仿射性结构解,即P(t,T)=exp(A(t,T)-rB(t,T)-V C(t,T)),其中A=A(t,T),B=B(t,T)及C=C(t,T)满足下面的常微分方程组,即

其终端条件为A(T,T)=B(T,T)=C(T,T)=0.显然在给定终端条件下B(t,T)的解析解为B(t,T)= (1-e-a(T-t))/a.而常微分方程(4)是一个众所周知的Riccati方程.由于该方程的系数是关于时间变量的函数,因此一般没有解析解,所以将使用数值方法求解.若给定C和B的解,则A的解为

3　参数校正方法

不失一般性,假设债券价格是从当前时刻开始观察.为了能给出参数估计方法,首先需要处理隐含状态变量Vt.对于本文的问题,将利用不同到期日可观测的债券价格数据近似随机波动率.

设R(t,T)为在t时刻到期日为T的零息债券收益率,则

假设R(t,T1)和R(t,T2)是两个不同到期日收益率(T1/=T2),可得

从式(5)和式(6)可得

其中Am=A(t,Tm),Bm=B(t,Tm)及Cm=C(t,Tm),m=1,2.

为了简化,在实际应用中对于表达式(7)通过线性组合来近似其动态的过程,即

其中α0和α1是常数.显然式(8)仅依赖于参数α0,α1及a.比较动态过程(2),辅助过程(8)简化参数估计过程.

下面将通过式(1)和辅助过程式(8)建立似然函数并给出半参数估计方法.

设Δt=ti-ti-1(i=1,2,...,N),其中tN是最大的观察值及t0=0.式(1)的欧拉离散形式为

其中ri=rti,Vi=V(ti),θi=θ(ti)及zi+1是一个服从标准正态分布的随机数.若给定Vi,式(9)的离散式是有偏的.尽管在给定V的条件下,随机微分方程(1)有解析表达式[24],但是,如果Δt足够小,有偏的现象将会减少.实际上,Glasserman[26]论述了式(9)的离散式是可行的.相应式(8)的离散过程为

根据式(9)和式(10),似然函数为

其中c是不依赖于θi和η的常数,η=(a,α0,α1),f(·|·,·,·)是条件密度函数,ri是r=(r0,r1,...,rN)的分量,i=0,1,2...,N.

为了估计θ(t)(其离散值为θi),引入众所周知Nadaraya-Watson核函数估计[20].那么θ(t)可近似为

下面将给出基于时间序列数据的两因子模型极大似然估计方法.基于式(11)和式(12),似然函数近似为

其中Vi用式(10)来近似计算.

注意到,若直接最大化似然函数式(13),其过程比较复杂,因此基于Simar等[27]的思想,采用两阶段估计方法.其核心思想是把上述问题化为两个简单的问题:一个非参数问题;一个全参数问题,其算法如下:

步骤1给定一个初值η0;

步骤2求优化问题(13),即

其中Ω(η)是参数η所在的领域;

步骤4重复步骤2和步骤3直到收敛.

显然,在给定参数η条件下,优化问题(14)转化为一个标准的非参数估计问题,即

接下去部分,将回答这两个问题.首先考虑算法步骤2,若给定真实的η∗,当h→0,θh(t,η∗)能否依概率收敛到相应的真实值θ∗.为了证明其相容性,需要下面的假设.

假设1在给定η条件下,假设Yi的真实密度函数为f(Y|η),其均值和方差满足下面的条件,即

其中Var(·)表示方差.

假设1说明了在使用数据时,相应的均值和方差是有界的.现实中,瞬时利率的时间序列数据的均值和方差一定是可满足上面条件的.而且从假设1可以得出二阶矩是有界的,即E[Y2]=Var(Y)+(E[Y])2＜∞.这个条件保证θ(η,t)是均方收敛的,从而可以得到定理1的结果.根据假设1,给出下面相容性定理,其证明过程可参考文献[28]中的性质3.1.1.

定理1假设1成立.如果Nh→∞和h→0那么有

定理1说明了,若给定真实值η∗,通过优化问题(14)所得θ值将概率收敛到θ∗.因此,需要进一步考虑优化问题(15)的相容性问题.此时,需要一些正则性假设.

假设2假设Ω(η)是紧的.θ∗=θ∗(t)及η∗是最大似然函数(13)的真实解且是Ω(η)的内点.

假设2表明了在算法中对于常系数取值必须是有界的,而在实际应用中取有界的常系数是显然的.另一方面假设解是Ω(η)的内点是数学上技术处理.

假设3定义下面的极限存在且一致收敛,即

进一步假设,当θ=θ∗,d(η;θ∗)=0解是唯一,即η=η∗.

假设3,实际是Kullback等[29]相对熵的概念.若假设ℓ(η∗,θ∗)的真实密度函数为f(r|η∗,θ∗)＞0,根据中心极限定理直接获得

基于文献[29]中引理3.1,d(η)≤0,而且等号成立当且仅当η=η∗.

假设4假设给定η,ℓ(η,θ)关于θ(t)是Lipschitz连续且Fr´echet导数存在并有界.另一方面,给定θ,∇ℓ(η,θ)向量的每个元素存在且Lipschitz连续.矩阵∇2ℓ(η,θ)每个元素有定义并Lipschitz连续,而且该矩阵是可逆的.

在上面的正则性假设条件下,下面定理说明了算法中式(15)的相容性性质.

若假设3成立,那么有下面相容性估计

证明根据定义

根据假设4及定理1,显然式(18)成立.基于文献[30]中定理5.7,式(18)成立隐含着式(19)成立.证毕.最后,给出算法中式(15)渐近性.首先,需要给出Fisher信息矩阵.

定理3设假设1～ 假设5成立,那么有下面的渐近性,

证明根据极大似然估计方法,优化问题(13)在极值点上梯度为零,即

其中˜η∈U(θ∗)⊂Ω(η).

通过简单的代数运算,重写上面等式为

为了证明上面等式依分布收敛,需要分开处理这个问题.首先,有

最后依概率收敛是根据定理1结论.根据极大似然定义及中心极限定理,上面极限是服从零均值方差为I(η∗,θ∗)的正态分布.

现在给出Hesse矩阵的估计,即

显然根据定理1及定理2,上面等式依概率收敛到I(η∗,θ∗).证毕.

4　实证分析

由于我国债券数据的不完整性,因此将使用美国债券数据.根据Durham[31]的结果,选取每周交易3个月到期日的债券收益率近似无风险短期利率,其时间从2000–01–07—2011–12–30,总的数据为629(数据来源于http://www.ustreas.gov).Balduzzi等[15]论述了使用不同的期限债券近似波动率是没有显著的差别,因此本文将使用到期日为1年和2年的债券数据,时间步长为1/52.图1描述了市场数据.江良[18]使用同样的数据来比较Vasicek模型和Hull-White模型的似然函数值,而且也得出了Hull-White模型的似然函数值稍微地改善的结果,但为了比较模型的有效性,这些结果也将列出来.

基于H¨ardle等[20]的结果,通过拇指原则,对于高斯核函数,最优宽度h=¯σ(4/(3N))1/5,其中¯σ是分布函数的标准方差,而且¯σ可近似为

为了区分不同h值所对应估计值,设h1,h2分别表示通过式(20)及式(21)近似获得,而且也设h3为¯σ= 1近似.

图1　2000–01–07—2011–12–30市场数据.Fig.1 Market data from 2000–01–07 to 2011–12–30.

表1列出了不同模型的参数估计值.对Vasicek模型和FV模型,长期均值分为θ/a=0.005 1和θ/a= 0.022 8.当考虑均值函数时,基于HW模型,显然窗口h=h1时,似然值最大;对于SVHW模型,选取h=h2时,似然函数值最大.对比表1中的似然函数值,Vasicek模型拟合效果最差,SVHW(h=h2)拟合效果最好.而且观察表1中的数据,基于FV模型的似然函数值明显比单因子模型的似然函数值要大.这一结果表明了两因子模型比单因子模型能更好地刻画市场数据;另一方面,对于单因子模型考虑随机波动率比考虑均值函数影响要大,如FV模型与Vasicek模型的似然值比较,其似然比值为1.378 7;HW模型与Vasicek模型的似然比值为1.140 8.而对于FV模型,考虑均值函数是必要的,如:当h=h2,SVHW模型的似然函数值比FV模型的似然函数值要大,大约为1 700.

表1　不同模型的参数估Table 1 Parameters estimates for the different model

图2描述了HW模型和SVHW 对于不同窗口h选取所对应θ(t)的数值结果.观察图2中的图形,若长期均值过度地拟合,导致数值结果出现激烈震荡.这种现象很难给出参数的预测值和相应的衍生品定价,而且业界也不喜欢不稳定的数值结果.结合表1中的数据,显然对于单因子模型,若考虑数值结果的稳定性,均值函数的模型对于拟合效果只是稍微地改善.这就意味着对于实践者若使用单因子模型,就应该权衡拟合的效果和数值稳定性.进一步观察图2可知,有一些数值解是负的.对于高斯模型,短期利率取负的概率是大于零,因此负的θ(t)值是有可能的.而且负的值表明了投资者对已实施政策的态度是消极的.

观察图2,考虑均值函数有力地解释了2008年发生次贷危机前后,投资者对于政府和美联储救市行为的态度变化.但是对于常系数模型,这种现象是很难解释的.如在2008年发生次贷危机时,不管美联储不断下调利率,但是投资者的长期预期利率还是下降.而在2008年10月份,通过美国政府救市,投资者的长期预期利率值有明显的上升,这种现象持续到2009年年初,投资者对整个预期收益率又回落.而后联邦储备局通过购买国债救市,这就导致投资进一步对将来的预期收益率恢复了信心.因此,考虑均值函数不仅对数据拟合效果有了改善,而且为中央银行和政府对于实施政策的有效性提供了较好的参考依据.

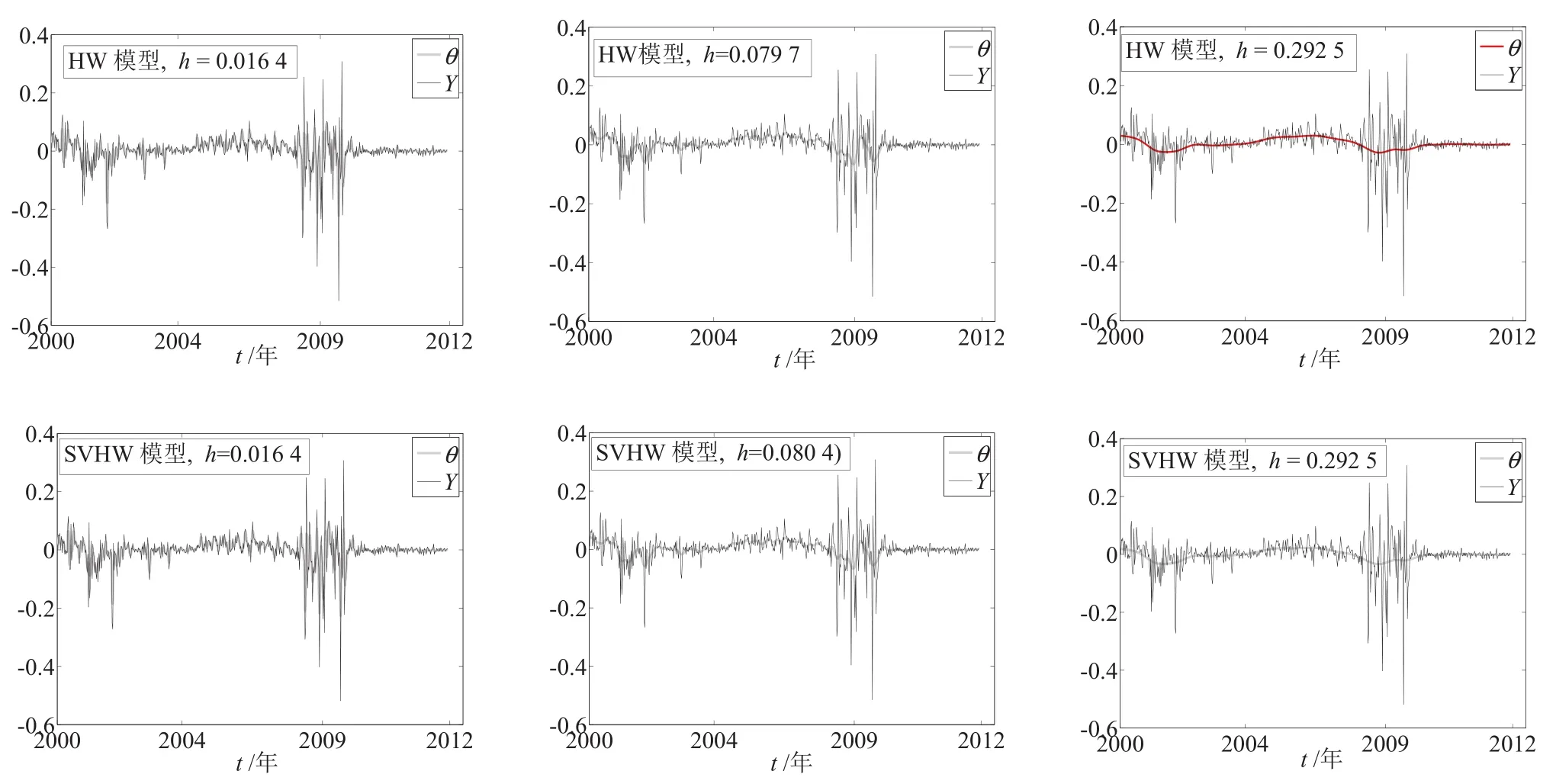
图2　基于 HW模型和SVHW模型对于不同窗口h的θ(t)数值结果Fig.2 The numerical results θ(t)for the different bandwidth h based on HW model and SVHW model

观察表1中的数据和图2,当h=h1时,基于SVHW模型,θ(t)函数的拟合效果最好,但是不稳定,其似然函数值明显比h=h2时似然函数值要小.这就说明了引入随机波动率和均值函数是有必要的.

图3显示了SVHW模型对不同窗口选取所对应的瞬时波动率.

图3基于SVHW 模型对于不同窗口h所对应的瞬时波动率(V)Fig.3 The spot volatilities(V)by the different bandwidth h based on SVHW Model,

图4画出了FV模型的瞬时波动率.观察图3和图4,当h=h1,h3时,其瞬时波动率没有明显的差异,这种现象和表1中的似然函数值保持一致,因此当选取h=h1,h3时,考虑长期均值是没有必要的.然而当h=h2时,其图像有着显著的差异,而且似然函数值也明显改善.比较SVHW(h=h2)模型的瞬时波动率,FV模型的瞬时波动率被高估了.

表2列出了水平短期利率和波动率的相关系数估计值.观察表2中数据,对于SVHW模型,当h= h1,h3时,相关性系数估计值和FV模型所得的估计值没有显著的差异.对于SVHW(h=h2)模型,相关性系数估计值最小,但所对应的似然值是最大的(看表1中的数据).此外,观察图1、图3和图4,瞬时利率和波动率运动的趋势是相同的.这种现象表明它们之间的相关系数一定为正的(参考表2中的数据).

图4　基于FV模型的短期波动率Fig.4 Spot volatility for FV Model

表2　短期利率和短期波动率水平相关性估计值Table 2 Correlation coefficient estimates between the short interest rate and the spot volatility

5　结束语

众所周知,不断地合理引入状态变量,其相应的模型拟合效果将变得更好.但是基于模型的衍生品定价的维数也会增加,这就导致衍生品定价数值方法变得更加困难.因此本文考虑随机波动率和均值函数的两因子模型.为了表明模型的合理性,本文选取时间序列数据,采用核函数估计方法并对随机波动率通过一个辅助的过程近似进行参数估计.进一步给出了估计方法的相容性和渐近性性质.

实证分析表明了,考虑随机波动率和均值函数是必要的,而且均值函数的假设对于系数校正效果有明显的改善.但是对于单因子模型可能考虑均值函数需要根据实际应用的情况而定.另一方面,考虑均值函数能够很好地解释一些金融市场的行为,特别是给政府和中央银行对已实施政策的有效性提供了很好的参考依据.因此可以断言,SVHW模型比单因子模型及FV模型更加有效.对于业界,可以在不增加状态变量的情况下,使用更好的模型进行衍生品定价.在进一步研究中,将考虑基于债券价格数据(横截面数据)两因子的参数估计方法并给出SVHW模型的衍生品定价.

[1]杨宝臣,李彪.基于最优动态利率模型的认股权证定价研究.系统工程学报,2009,24(3):264–271. Yang B C,Li B.Research on warrant pricing based on optimal dynamical interest rate model.Journal of Systems Engineering,2009, 24(3):264–271.(in Chinese)

[2]Hull J,White A.Pricing interest-rate-derivative securitites.The Review of Financial Studies,1990,3(4):573–392.

[3]Dai Q,Singleton K.Specification analysis of affine term structure models.The Journal of Finance,2000,55(5):1943–1978.

[4]Duffie D,Kan R.A yield–factor model of interest rates.Mathematical Finance,1996,6(4):379–406.

[5]Litterman R,Scheinkman J A.Volatility and yield curve.Journal of Fixed Income,1991,1(1):49–53.

[6]Kim D H,Singleton K J.Terms structure models and the zero bound:An empirical investigation of Japanese yields.Journal of Economics,2012,170(1):32–49.

[7]Cheridito P,Filipovic D,Kimmel RL.Market price of risk specifications for affine models:Theory and evidence.Journal of Financial Economics,2007,83(1):123–170.

[8]Pierre C D,Goldsterin R S,Jones C S.Can interest rate volatility be extracted from the cross section of bond yields.Journal of Financial Economics,2009,94(1):47–66.

[9]Duffee G R,Stanton R H.Estimation of dynamic term structure models.Quarterly Journal of Financ,2012,2(2),1–51.

[10]Andersen TG,Lund J.Estimating continous-time stochastic volatilty methods of the short term interest rate.Journal of Econometrics, 1997,77(2),343–377.

[11]Fong G H,Vasicek O A.Fixed-income volatility management.Journal of Portfolio Management,1991,7(4):41–46.

[12]Longstaff F A,Schwartz E.Interest rate volatility and the term structure:A two-factor general equilibrium model.Journal of Finance, 1992,47(4):1259–1282.

[13]Surya B A.Two-dimensional Hull-White model for stochastic volatility and its nonlinear filtering estimation.Singapore:Procedia Computer Science,2011,4,1431–1440.

[14]Balduzzi P,Das S,Foresi S.The central tendency:A second factor in bond yield.Review of Economics and Statistics,1998,80(1): 62–72.

[15]Balduzzi P,Das S R,Foresi S,et al.A simple approach to three-factor affine models of the term structure.Journal of Fixed Income, 1996,6(3):43–53.

[16]Chen L.Interest Rate Dynamics,Derivatives Pricing,and Risk Management.Heidelberg:Springer Verlag,1996.

[17]范龙振,程南雁.一类均值为跳跃–均值回复过程的利率模型.系统工程学报,2011,26(3):298–305. Fan L Z,Chen N Y.Inerest rate model with jump-mean reverting stochastic mean.Journal of Systems Engineering,26(3):298–305. (in Chinese)

[18]江良.基于时间序列数据Hull-White模型半参数估计方法.莆田学院学报,2013,20(5):1–4 Jiang Liang.Semi-parametric estimation for Hull-White model via time series data.Journal of Putian University,2013,20(5):1–4. (in Chinese)

[19]Grzelak L A,Oosterlee C W,Weeren S V.Extension of stochastic volatility equity models with the Hull-White interest rate process. Quantitative Finance,2012,12(1):89–105.

[20]Härdle W,Müller M,Sperlich S,et al.Nonparametric and Semiparametric Models an Introduction.Berlin:Springer,2004.

[21]Ramsay J O,Silverman B W.Functional Data Anaysis.New York:Springer Verlag,2005.

[22]Aït-Sahalia Y,Kimmel R.Maximum likelihood estimation of stochastic volatility models.Journal of Financial Economics,2007, 83(2):413–452.

[23]Cox J C,Ingersoll J E,Ross S A.A theory of the term structure of interest rates.Econometrica,1985,53(2):385–407.

[24]Brigo D,Mercurio F.Interest-rate Models:Theory and Practice.Berlin:Springer Verlag,2006.

[25]Vasicek O A.An equilibrium characterization of the term structure.Journal of Financial Economics,1977,5(2):177–188.

[26]Glasserman P.Monte Carlo methods in Financial Engineering.New York:Springer Verlag,2003.

[27]SimarL,Wilson PW.Estimation and inference in two-stage,semi-parametric models of production process.Journal of Econometrics, 2007,136(1):31–64.

[28]Härdle W.Applied Nonparametric Regression,Econometric Society Monographs.Cambridge:Cambridge University Press,1990.

[29]Kullback S,Leibler R A.On information and sufficiency.Annals of Mathematical Statistics,1951,22(1):79-86.

[30]Van Der Vaart A W.Asymptotic Statistics.Combridge:Combridge University Press,1998.

[31]Durham G B.Likelihood-based specification analysis of continuous-time models of the short–term interest rate.Journal of Financial Economics,2003,70(3):463–487.

Parametric estimation of Hull-White model for stochastic volatility

Jiang Liang1,Lin Hongxi2
(1.School of Mathematics,Putian University,Putian 351100,China; 2.School of Business,Putian University,Putian 351100,China)

A two-factor model of stochastic volatility is established.A two-stage semi-parameter method is applied to estimate constant coefficient parameters of this model.Moreover,kernel estimator method is developed to estimate the long-term mean value function,by this method the consistency of the two-stage method and the asymptotic normality of parameters are obtained.The empirical results show that the likelihood function can be improved in the long-term mean value model rather than the constant coefficient model.Also,the model provides a good explanation for the effective policies implemented by the central bank and the government. Besides,the industries can use the above model for valuing interest-rate-derivative securities without increasing the dimension.

long-term average value;stochastic volatility;short term interest rate model;semi-parameter estimation;kernel estimation method

F830.9;O212.7

A

1000-5781(2016)05-0633-10

10.13383/j.cnki.jse.2016.05.008

2013-12-20;

2014-05-02.

国家自然科学基金资助项目(11471175);福建省自然科学基金资助项目(2015J05012;2016J01677);莆田学院育苗基金资助项目(2014060;2014061).

江良(1978—),男,福建莆田人,博士,副教授,研究方向:金融工程和金融计算,Email:ptjliang@163.com;

林鸿熙(1969—),男,福建莆田人,硕士,教授,研究方向:演化博弈论及其应用,Email:linhongxi@163.com.