Optimization of Air Route Network Nodes to Avoid ″Three Areas″ Based on An Adaptive Ant Colony Algorithm
2016-11-21,,,
,,,
College of Civil Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, P.R. China
Optimization of Air Route Network Nodes to Avoid ″Three Areas″ Based on An Adaptive Ant Colony Algorithm
WangShijin*,LiQingyun,CaoXi,LiHaiyun
College of Civil Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, P.R. China
(Received 22 August 2015; revised 16 November 2015; accepted 5 January 2016)
Air route network (ARN) planning is an efficient way to alleviate civil aviation flight delays caused by increasing development and pressure for safe operation. Here, the ARN shortest path was taken as the objective function, and an air route network node (ARNN) optimization model was developed to circumvent the restrictions imposed by ″three areas″, also known as prohibited areas, restricted areas, and dangerous areas (PRDs), by creating a grid environment. And finally the objective function was solved by means of an adaptive ant colony algorithm (AACA). The A593, A470, B221, and G204 air routes in the busy ZSHA flight information region, where the airspace includes areas with different levels of PRDs, were taken as an example. Based on current flight patterns, a layout optimization of the ARNN was computed using this model and algorithm and successfully avoided PRDs. The optimized result reduced the total length of routes by 2.14% and the total cost by 9.875%.
air route network planning; three area avoidance; optimization of air route network node; adaptive ant colony algorithm; grid environment
0 Introduction
In recent years, with the rapid development of aviation industry, sustained growth of air traffic has caused airspace congestion, flow control flight delays, and other problems more and more serious. The air route network (ARN), whose structure determines the operational efficiency of traffic flow and transportation costs, is the physical space where air traffic takes place. ARN planning is an effective way to allocate and use airspace resources rationally, eliminate airway bottlenecks, and ensure aviation safety.
Riviere achieved and improved global ARN optimization technology to attain the objective of minimum cost or distance, using a grid covering whole Europe and based on the no-sector concept proposed by Dudong[1-2], as shown in Fig.1. The operating characteristics of China′s airspace control have led Chinese researchers to air route network node (ARNN) local optimization technology to attain the objective of minimum cost of distance[3-7]using optimization problem-solving thinking and intelligent optimization algorithms.
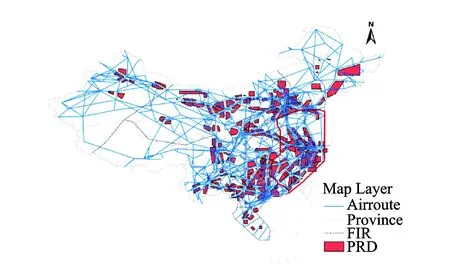
However, the research has barely addressed the inevitable restrictions of the airspace structure in the process of ARN optimization. China′s airspace contains many ″three areas″, also known as the prohibited areas, restricted areas, and dangerous areas (PRDs), which are unavailable airspace for ARN optimization, and ″fragment″ the optimization environment exhibit, as shown in Fig.2. Two studies have considered airspace environment restrictions in ARN optimization. On the one hand, the MAKLINK graph model proposed by Zhao and restricted by the number, shape, and layout of PRDs can avoid convex PRDs, but does not apply to concave PRDs, which severely limits its applicability[8]. On the other hand, Wang successfully completed an ARN design while avoiding various PRD shapes by using cellular automata (CA), but this approach is restricted by the complexity of rule-making[9], which reduces its overall efficiency.
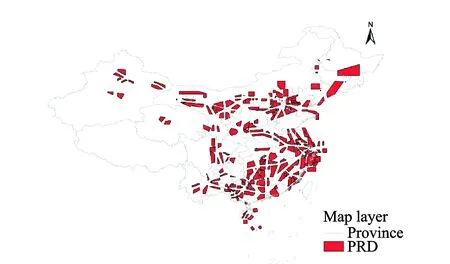
Fig.2 ARN optimization ″fragmented″ environment
The concept of ground mobile robot path planning is to establish an abstract model of the path using a grid method[10-12]and then to use a genetic algorithm (GA) to achieve obstacle avoidance and path planning in a position environment using binary coding. However, the length of code increases with the number of grid cells, leading to a high computational complexity. This method is applicable only to grid sizes of not more than 16×16 problems. To solve this problem, Zhang[13-14]redefined the insert and delete operators. This method is simple, and its search ability is powerful, but the problem that the GA chromosome is too long is still not resolved. Zhang[15]used the ant colony concept and chose the distance from the target and the pheromone concentration in the direction of motion as heuristic factors, an approach working well. However, this algorithm takes a long time to search and easily stagnates.
In this context, improving solution efficiency while achieving spatial PRD avoidance would be very helpful. According to the relative positions of the current node and the destination node, an adaptive ant colony algorithm (AACA) combined with a certain selection probability and a random selection strategy in a grid environment was proposed. The AACA was used to solve the ARNN optimization model with a shortest-path objective function, avoiding PRD boundaries. Then five typical routes across different numbers of PRDs in the ZSHA airspace were selected as an example to verify the feasibility of the algorithm.
1 ARNN Optimization Model
1.1 Assumptions in ARNN optimization model
When building the ARNN optimization model (considering only the ARN, without the approach control area and terminal control area), the following assumptions were proposed:
(1) Aircraft fly along the center line of the route;
(2) ARN is a two-dimensional plane network which does not consider the climb or descent of aircraft;
(3) Aircraft fly at a constant speed on the route and are uniformly distributed with equal spacing;
(4) Aircraft arrive at and leave an intersection point in the same direction, and the intersecting tracks consist of plane linear segments;
(5) PRDs cannot be traversed, but the PRD boundary mentioned earlier is the extended one, which belongs to the safety zone.
1.2 Establishment of ARNN optimization model
ARN can be described as follows
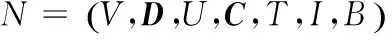
(1)
whereV(N) is the set of ARNN. There are two kinds of nodes: Intersection points and airport points.n,mrepresent the number of intersection points and airports, respectively
(2)
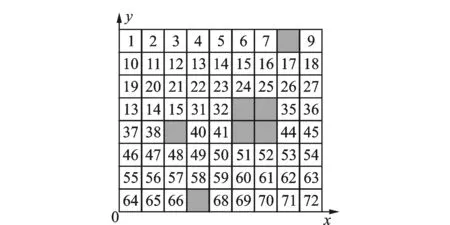
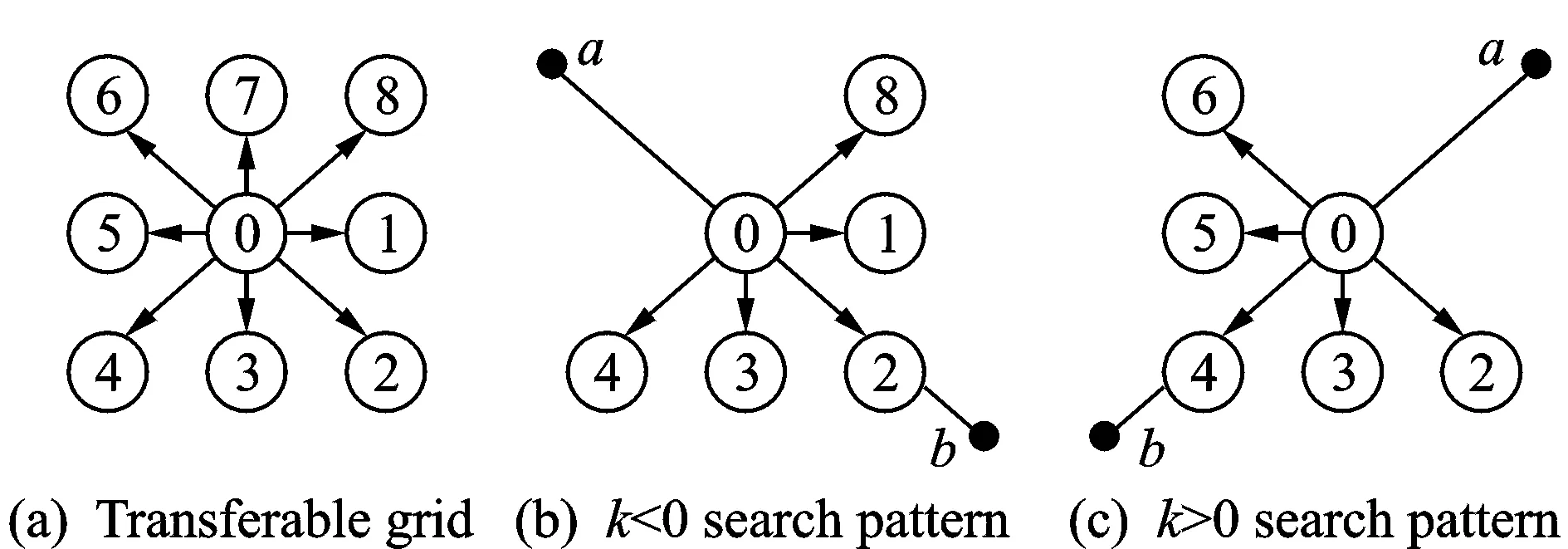
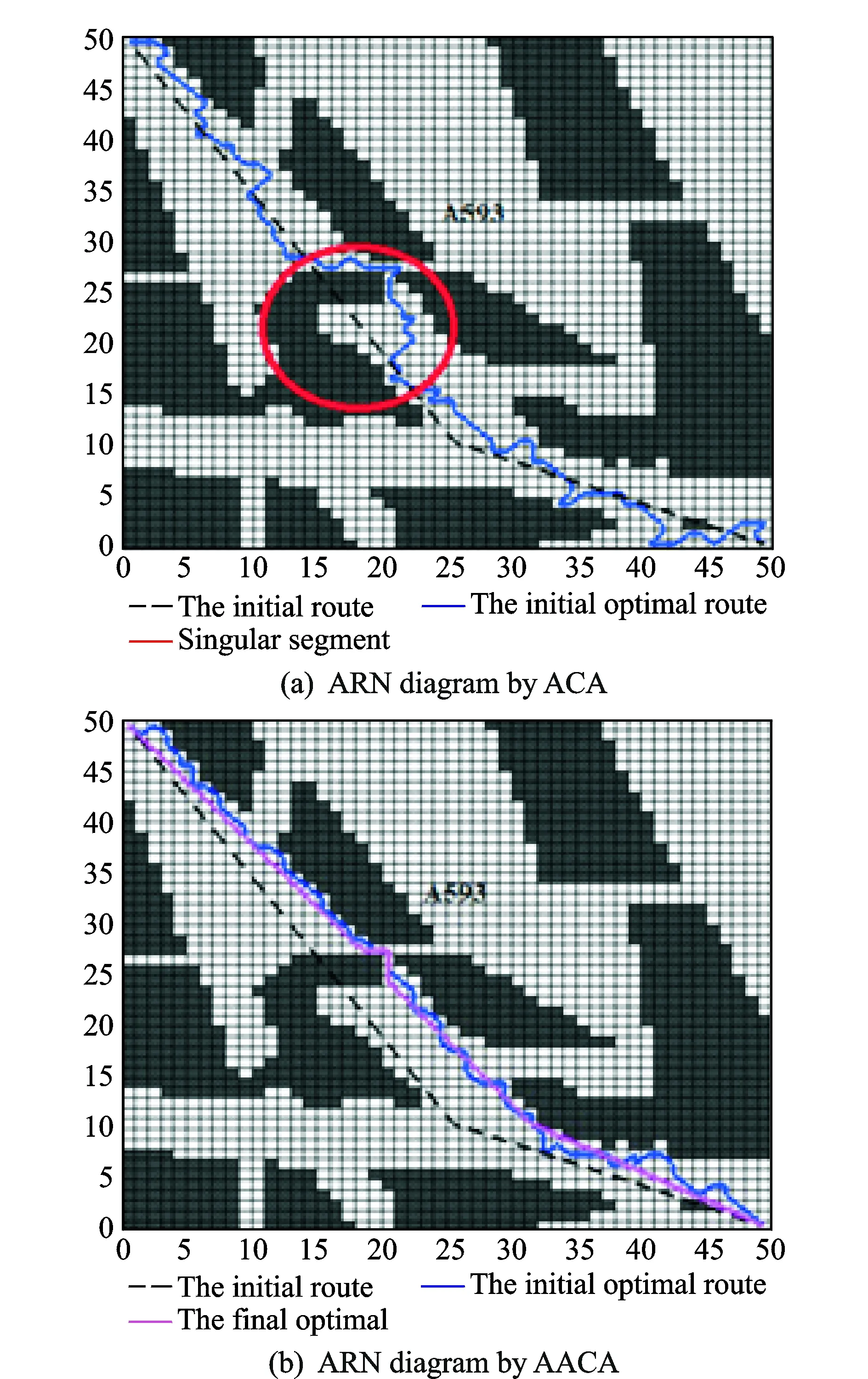
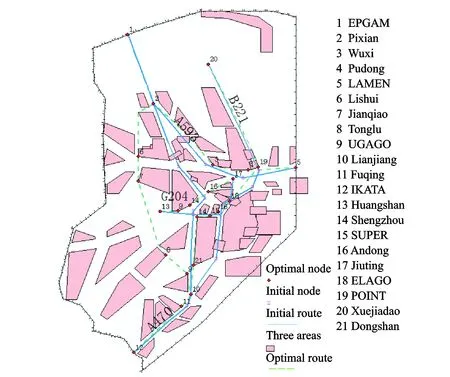
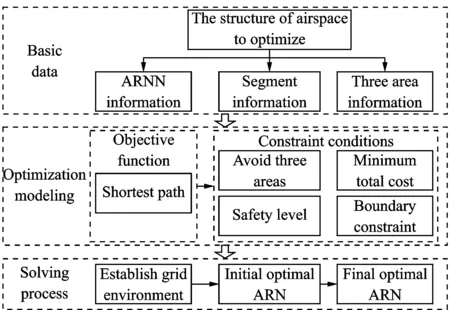
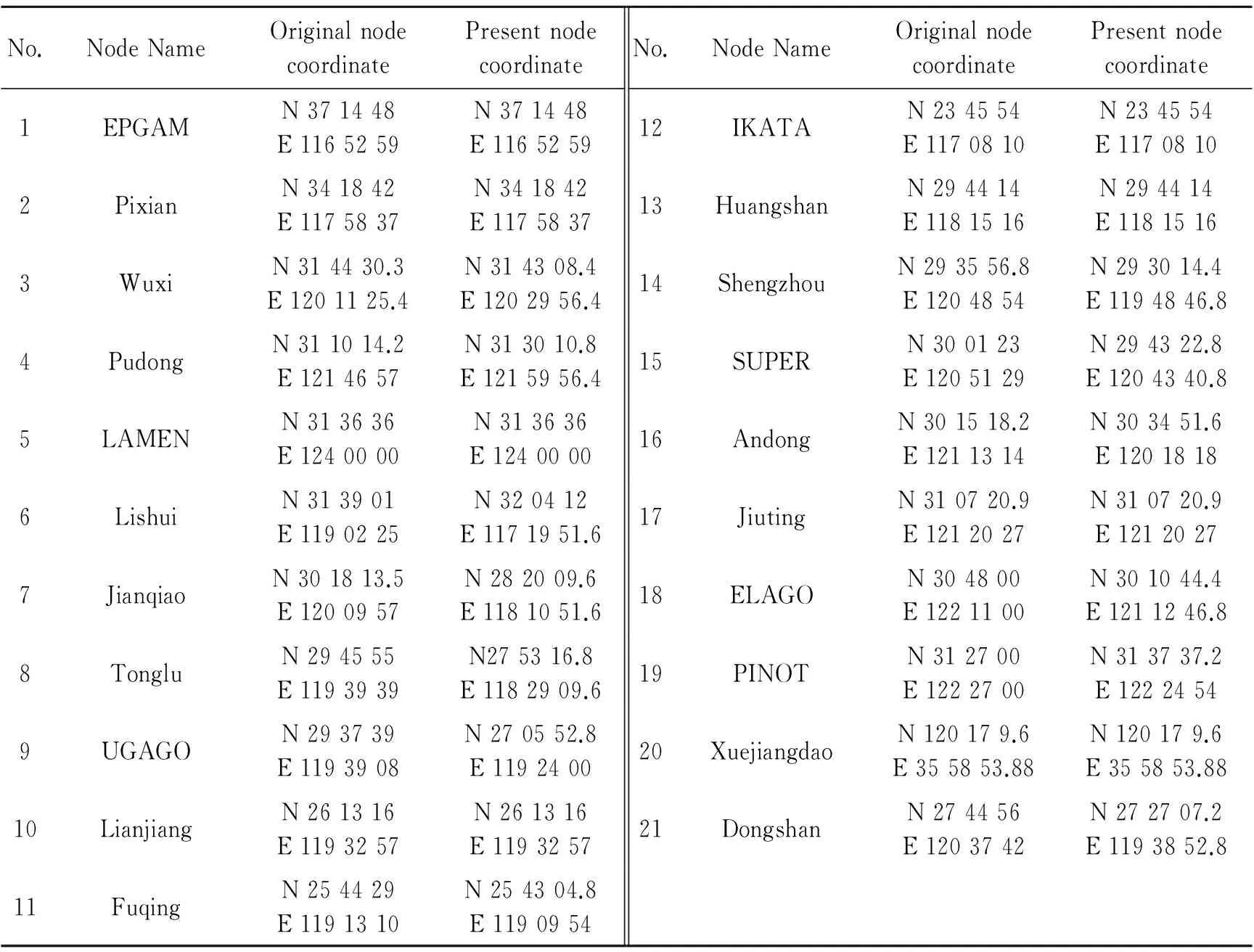
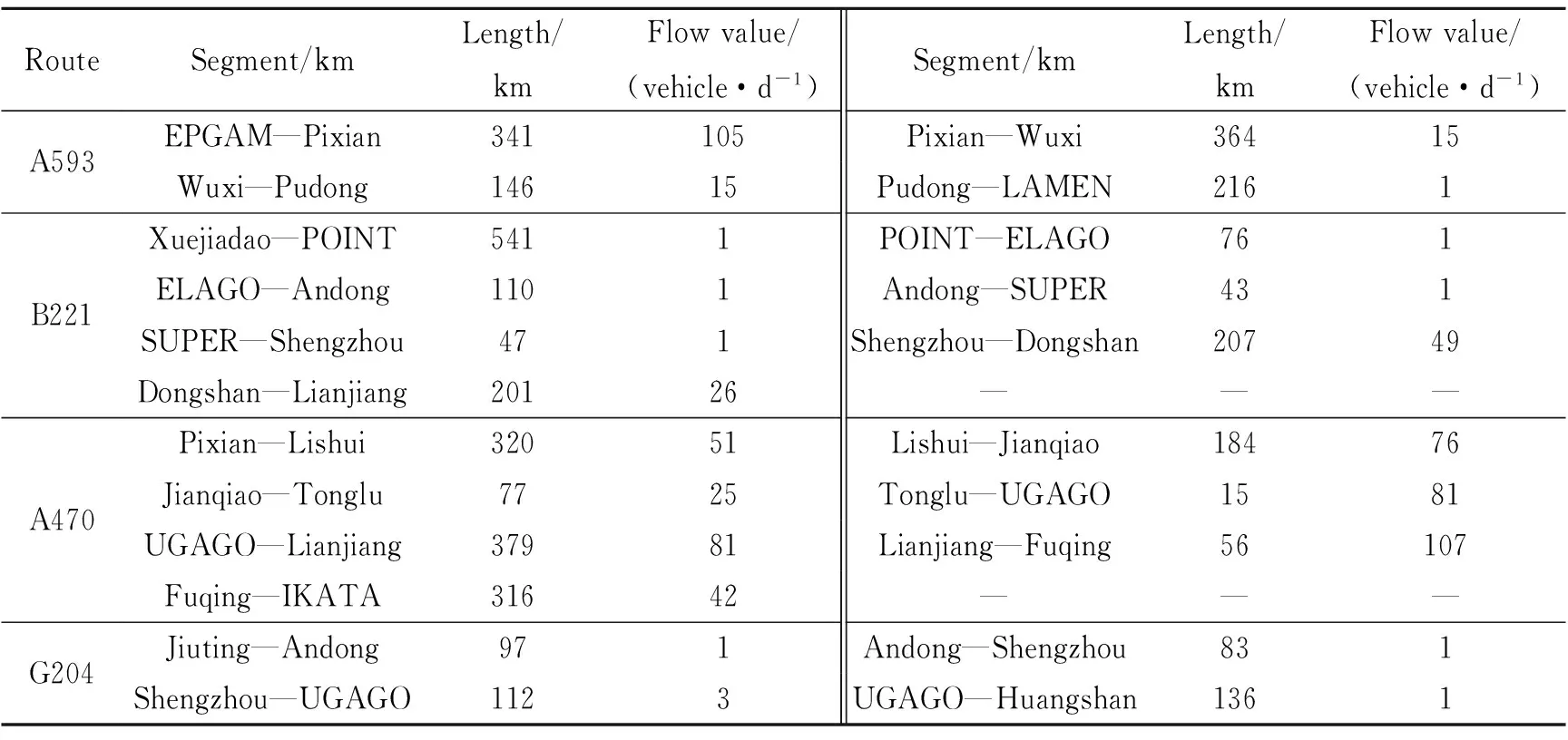
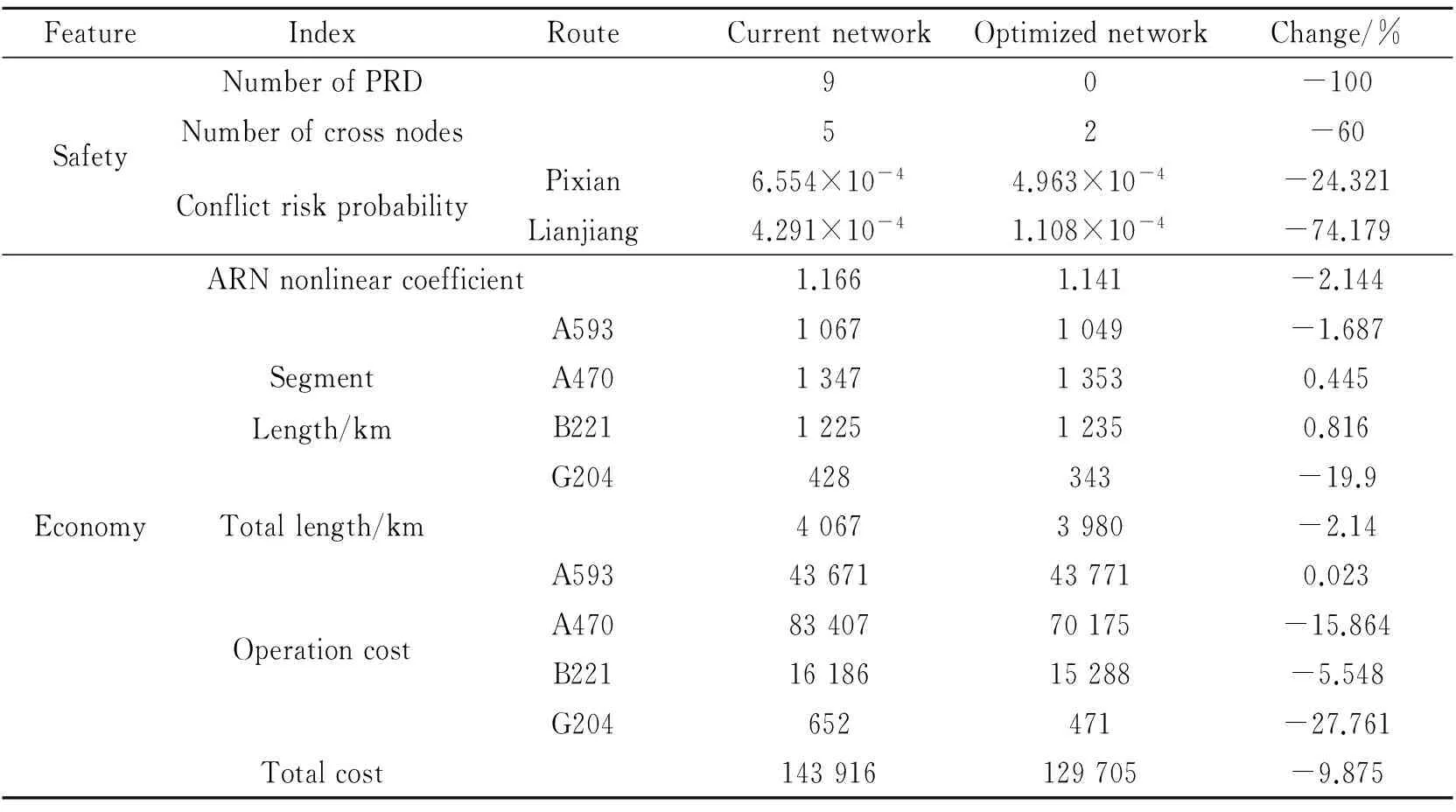
where the location of viisexpressedby(xi,yi), virepresentsanintersectionpoint,ifi≤ n,andanairport,ifn D(N) is a matrix of the segment lengths between pairs of nodes in the ARN. (3) where dijrepresentsthelineardistancebetweeniandj (4) U(N)meansthesegmentsconnectedbynodes(includingthenodes)cannotbeinU(N),whichcanbedescribed (5) whereΦrepresentstheemptyset. C(N) means potential flight conflict risk probability of the set of intersection points (6) where cireflectsairspacesafetyandcanberepresentedas (7) wherecirepresentsthehourlyaveragepotentialflightconflictriskprobabilityofARNNnodesvi; fjiandfkirepresenttheflightflowsofsegment(vj,vi)and(vk,vi),respectively; Xrepresentsthecruisingspeed(km/h); Ythelateralseparationstandard(km)underradarcontrol; αjiktheintersectionangleofsegments(vj,vi)and(vk,vi); Sthenumberofintersectingsegmentsonvi;andcmaxthethresholdvalueofthehourlyaveragepotentialflightconflictriskprobabilityofARNN. T(N)isthetotalcostofflightpaths,whichcanserveasameasureofARNeconomy;thelowerthetotalcost,themoreeconomicalthenetworkis (8) I(N)isthenonlinearcoefficient,definedastheratiooftheactuallengthandthelinearlengthbetweenARNNs.ThenonlinearcoefficientofthenetworkcanbeusedtomeasuretheconvenienceoftheoverallARN;thelargeritsvalue,thehighertheflightcosts,andthelowertheairspaceutilization (9) wheredijandGijrepresenttheactuallengthandthelinearlength,respectively,betweentwonodesi, j. B(N)istheboundaryconstraintofARNNs.ThesignificanceofthisconstraintisthatARNNsmustbelocatedintheplanningarea (10) TheARNNoptimizationmathematicalmodelcanbedescribedbyEqs.(11)—(14).Eq.(11)istheshortest-pathobjectivefunction;Eqs.(12)—(14)areconstraints;Eq.(12)isthePRDrestrictiononthesegmentstooptimize;Eq.(13)maintainsthesafetyleveloftheintersectionpoints;andEq.(14)limitstheboundarytotheplannedARN (11) (12) (13) (14) 2.1 Establishing ARN grid environment The grid method is used to divide the ARN airspace into a regular and uniform grid. The grid is divided into two states: An obstacle grid and a free grid. Fig.3, for example, establishes an 8×9 grid environment and specifies the left bottom corner as the coordinate origin. Using the lateral direction as thex-axis and the longitudinal direction as they-axis, a rectangular coordinate system is established. Now set PRDs and the flight corridor as an obstacle grid (black grid) and a free grid (represented by grid numbers), respectively. PRD accounts for one or more of the grid cells; if it is less than one grid cell, the incomplete cell is regarded as a complete grid cell. There are at least two free grid cells between disjoint obstacle grid cells. The location of the start and the end points can be anywhere in a free grid, but the aircraft can move only one step to an adjacent grid cell. All grid cells are identified using a combination of a serial numbering method and the rectangular coordinate system. (1) Serial numbering method Starting from the lower left corner of the grid in Fig.3, all grid cells are numbered from left to right and from top to bottom. The serial numbernranges from 1 to 72. An identified grid cell is referred to asgn. The grid cell with serial number 1 is referred to asg1, as shown in Fig.3. Fig.3 Relations between grid coordinates and serial numbers (2) Rectangular coordinate method The grid geometric center of the rectangular coordinates is defined as the grid coordinatesg(x,y). The serial number 1 of the grid cell in Fig.3 isg(0.5,0.5). The correspondence between the coordinates and the serial numbers of a grid cell is given x=mod(i-1,Nx)+0.5 (15) whereNxis the serial number of the lateral grid cell, mod is a remainder operation to solve, and fix is a discard remainder rounding operation. 2.2 Adaptive ant colony algorithm A traditional ant colony algorithm (ACA) search pattern can be used to solve the problem of two-dimensional ARN planning. As shown in Fig.4(a), the aircraft is located in the center grid cell 0, and the remaining eight adjacent grid cells are transferable grid cells (excluding obstacle grid cells and grid cells already traversed). This search pattern takes much time, and it is easy to encounter singular segments. Fig.4 Search pattern The AACA was proposed in this paper with a selection strategy which combined deterministic selection and probabilistic random selection. On the one hand, deterministic selection determines the search strategy according to the relative positions of the optimized nodes. Assume that the direction of the search path is fromatob. Regardless of vertical and horizontal special cases, the relative positions of ARNN fall into two cases: the slope between two nodesk<0 (as shown in Fig.4(b)) andk>0 (Fig.4(c)). Further, assume that the aircraft is located at grid cell 0, which belongs to segmentab. The aircraft flies fromatob, and only the adjacent five grid cells 1, 2, 3, 4, and 8 (excluding obstacle grid cells and grid cells already traversed) are passed through. Ifk<0, the algorithm proceeds in a similar manner. The aircraft flies fromatob, and only the adjacent five grid cells 2, 3, 4, 5, and 6 (excluding obstacle grid cells and grid cells already traversed) need to be searched ifk>0. If the ″ants″ do not have a subsequent grid cell to choose, they can be seen as having fallen into a trap, and an ″ant fallback strategy″ is used to ensure that they reach their destination safely. On the other hand, probabilistic random selection refers to the use of a ″roulette wheel″ to select the next grid cell and dynamically adjust the deterministic choice probabilities during the search process. The direction of search is ensured to reduce the number of search grid cells and singular segments. For example, international route A593 passes through two PRDs. According to Section 2.1, a 50×50 array was built in MATLAB in the form of a grid environment, as shown in Fig.5. Black and white grid cells represent PRDs and free flight areas, respectively. Traditional ACA was then used to search the neighboring eight directions for the optimal route. The broken line in Fig.5(a) represents the initial route, the solid line the optimal route as obtained by traditional ACA, and the segments in circles indicate obvious singular segments and redundant ARNN nodes after optimization. Aircraft do not fly in singular segments. The dotted line in Fig.5(b) indicates the initial optimal route, which has reduced the large number of singular segments using the AACA. Fig.5 ARN diagram by two algorithms 2.3 Process of solving the optimization model According to Section 2.1, a grid environment is established. The steps to solve the ARNN optimization model using AACA under the grid environment are as follows. Step 1 According to the structure of the airspace to optimize, the geographical position and the grid position, which are represented by theMpairs of starting and target nodes of the segment to optimize, are confirmed. The positional relation and search pattern of theMpairs of nodes are also confirmed. Step 2 The data and the ant taboo table are initialized. The initial pheromone of the path to optimize is set to a constant value, the number of ants tom, and the number of iterations toN.mants are then placed into the grid at the starting node, and the initial position of each ant enters the ant taboo table. Step 3 When the aircraft transfers, it is necessary to determine whether it has a selectable grid cell available. If not, the ant has fallen into a trap and must be removed from the simulation. Otherwise the ″roulette″ method is used to select the next grid cell where the aircraft can transfer. According to state transition of Eq.(16), the probability of the next selected grid cell is calculated and its transition probabilities are used as a cumulative probability, generating a random number. If the random number falls into the scope of one cumulative probability, the corresponding cumulative probability grid cell will be the following grid cell. This process is iterated until the destination grid cell is reached. Any ant that does not reach the destination grid cell are removed from the simulation. (16) whereαis a factor representing the elicitation of information,βthe desired heuristic factor,τij(t) the intensity of pheromone track (i,j) at timet; the heuristic functionηijis equal to 1/dj; anddjis the distance between the grid cell which can be chosen for transfer and the end of the grid, directing the ants search routes toward destination node. Step 5 The paths of all the remaining ants that reach the destination grid cell are revised. Curved paths between adjacent grid cells are straightened, and the total path length is reduced as much as possible. According to Eqs.(17)—(19), the pheromones on the paths which the remaining ants have traversed are updated (17) (18) (19) where Δτijis the amount of pheromone per unit length of trail that antkleaves on edge(i,j); 1-ρthe pheromone residual factor;Lkthe path length of antkin the search; andQthe intensity of the pheromone. Step 6 After iteration, the shortest path between each pair of nodes is output. By increasing the number of grid cells, the optimal path will be more precise. The final optimal ARN is then formed. Step 7 The constraints of the optimal final ARN are checked. According to the method in Ref.[16], the security level of ARNNs is verified. The optimal final ARN is then output. Otherwise, according to the severity and possible consequences of unsafe times or conditions, nodesci≥cmax= 1×10-3may be re-optimized. The national air routes and PRDs were visualized using ArcGIS, as shown in Fig.6. The term ″line″ refers to an upper air route, and an irregular ″block″ represents a PRD. The area outlined in bold lines is ZSHA. The density of air routes and PRDs shows that ZSHA is a typical busy airspace in China. ZSHA includes Jinan, Qingdao, Hefei, Shanghai, Xiamen, and Nanchang, six upper control areas, and 20 control sectors. It contains 11 dangerous airspaces and 55 restricted airspaces, including more PRDs than any other flight information region (FIR) in China. With the development of civil aviation, rapid growth of air traffic has led to a series of problems, such as ARN airspace congestion and flight delays. Fig.6 ZSHA location of schematic diagram Four representative international routes, G204, A470, B221, and A593 in ZSHA, were selected. Using MATLAB simulation platform, AACA was used to establish, solve, and verify the feasibility of the ARNN model in ZSHA based on the grid environment. Finally, the ArcGIS software was used to visualize the results before and after optimization, as shown in Fig.7, where the block sections represent PRDs; The solid line and the dotted line the initial route and the optimal routes respectively; the hollow rim and the solid rim represent the initial ARNN and the optimal ARNN respectively. The coding was marked as those in Ref.[17]. The numbers from 1 to 21 indicate the nodes traversed by the routes to be optimized. G204, A470, B221, and A593 passed three, two, three, and two PRDs. Fig.7 Comparison of ARN before and after optimization According to Part 2 (establishment of the optimization model) and Part 3 (solving the algorithm), the ARNN optimization process includes basic data, the optimization model, and solving the three modules, as shown in Fig.8. Fig.8 Module chart of ARNN optimization The basic data module in Fig.8 includes collection and pretreatment of basic data. It analyzes the airspace status quo in ZSHA and confirms the number and location of PRDs, segments, and ARNNs to optimize the ZSHA network, as shown in Table 1. According to airport informa-tion on takeoffs and landings, the annual flow was extracted from airports all over the country from flight plans in 2013. Then the average daily flow between airports was obtained. Air routes for each aircraft depend on No.1 Order of the Chinese Air Force[18]. According to routes and daily flow between airports, the daily flow in each segment was confirmed, as shown in Table 2. According to Eqs.(7)—(9), the known information was used to calculate the conflict risk probability for each node, the total cost, and the network nonlinear coefficient, as shown in Table 3. Table 1 Comparison of node coordirates between before and after optimization In the optimization module, the optimization model was developed for the G204, A470, B221, and A593 routes in ZSHA, and related parameters were set. According to Eq.(11), a shortest-path objective function was established. According to Eqs.(12)—(14), three constraint conditions were defined: avoiding PRDs, maintaining safety levels, and respecting boundary constraints. To solve the process module, according to Section 2.1, a grid environment was established for ZSHA, as shown in Fig.5. Then, as mentioned in Section 2.2, a search pattern was selected considering the relative positions of nodes. According to Section 2.3, aircraft search for the shortest path based on AACA; the dotted line in Fig.5(b) represents the initial optimization path for A593. By increasing the number of grid cells, the optimal final path was found, as shown by the solid line in Fig.5(b). Then any constraint conditions on the optimal final path were checked. The constraints expressed in Eqs.(12), (14) were implemented in the process of executing the algorithm, and therefore the initially optimized ARN should satisfy Eq.(13). The conflict risk probability of the ARNN was less thancmax1×10-3after calculation, as shown in Table 3. On the basis of these simulation results, the locations of the ARNNs before and after optimization are given in Table 1. A comparative diagram of the ARN before and after optimization is shown in Fig.7. The aggregated indicators of the optimized ARN were evaluated and analyzed, as shown in Table 3. Table 3 divides the optimization indicators into two categories: safety and economy. The former includes changes in the number of PRDs traversed, the number of nodes crossed, and the node hourly average potential flight conflict risk probabilities. This last includes changes in the ARN nonlinear coefficient, segment length, and operating cost. In the case of ZSHA, AACA successfully avoided nine PRDs which were traversed by routes G204, A470, B221, and A593. The number of intersecting nodes went from 5 to 2, a reduction of 60%. Under the conditions of the current flight flow, the flight conflict risk probability of the PiXian and LianJiang nodes was reduced by 24.321% and 74.179%, respectively, improving the safety level. The length of routes A470, A593, and B221 remained almost the same, but the length of route G204 was significantly reduced by 19.9%, resulting in a reduction of 2.14% in total route length. The nonlinear coefficient was reduced by 2.144% due to the shorter length. The cost of each route except for A593 was significantly reduced. The total cost of the four routes was reduced by 9.875%, improving the economic status of the ARN. Table 2 Segment and flow in ZSHA Table 3 Optimization results According to the relative position relationship of the starting and destination nodes, an AACA based on a grid model was selected to confirm the corresponding ant colony search mode. The optimization resulted in a decrease of 2.14% in total route length and a decrease of 9.875% in total operating cost, improving the operating economics of the ARN. The AACA optimization algorithm can reduce the number of search nodes, save computing time, improve optimization speed, and reduce the probability of singular segments. We will consider the interests of the airline from the perspective of airspace users, to establish a double ARNN optimization model, and to solve the optimization algorithm in future work. Acknowledgements This work was supported by the the Youth Science and Technology Innovation Fund (Science)(Nos.NS2014070, NS2014070). [1] VU D, GILLES G, NICOLAON J, et al. Sector-Less air traffic management [C]∥Air Traffic Management R&D Seminar. Santa Fe: AIAA, 2001: 1-7. [2] THOMAS R, PASCAL B. Shortest path in planar graph and air route network [C]∥Proceedings of the 4th Eurocontrol Innovative Research Workshop & Exhibition. France: Eurocontrol, 2005: 1-10. [3] ZHOU J. Research of the airspace en route network based on the bi-level programming [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2008. (in Chinese) [4] CAI K Q, ZHOU C. Optimization of the crossing waypoints in air route network [C]∥Digital Avionics Systems Conference (DASC). USA: IEEE, 2010: 2. E. 3-1-2. E. 3-8. [5] XIAO M M, ZHANG J, CAI K Q, et al. Cooperative co-evolution with weighted random grouping for large-scale crossing waypoints locating in air route network [C]∥Tools with Artificial Intelligence (ICTAI). USA: IEEE, 2011: 215-222. [6] XIN Zhengwei. Research on air route network planning technology [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013. (in Chinese) [7] CHEN Cailong. Research on optimization method based on complex network for crossing waypoints location [D]. Hefei: University of Science and Technology of China, 2011. (in Chinese) [8] ZHAO Shuang. Research on national trunk air route network design [D]. Beijing: Beijing University of Aeronautics and Astronautics, 2008. (in Chinese) [9] WANG S J, GONG Y H. Research on air route network nodes optimization with avoiding the three areas [J]. Safety Science, 2014, 66: 9-18. [10]GUO H T, ZHU Q B, XU S J. Rapid-exploring random tree algorithm for path planning of robot based on grid method [J]. Journal of Nanjing Normal University (Engineering and Technology Edition), 2007, 7(2): 58-61. [11]ZHU B, ZHANG Y L. An ant colony algorithm based on grid method for mobile robot path planning [J]. Robot, 2005, 27(2): 132-136. [12]KAZUO S, SMITH J. Genetic algorithms for adaptive motion planning of an autonomous mobile robots [C]∥Computational Intelligence in Robotics and Automation. USA: IEEE, 1997: 1-9. [13]ZHANG Y, WU C D, YU Q. Robot motion planning based on genetic algorithms [J]. Journal of Shenyang Arch And Civ Eng Univ (Natural Science), 2002, 18(4): 302-305. [14]HU Y L, ZHU L Z. The application research of genetic algorithm for the robot shortest path planning [J]. Machinery Design & Manufacture, 2002, 3(5):109-111. [15]ZHANG M Y, HUANG H, HAO Z F, et al. Motion planning of autonomous mobile robot based on ant colony algorithm [J]. Journal of Environment Sciences, 2005, 25(1): 35-38. [16]Industry Administration Office of Civil Aviation Administration of China. AP-83-TM-2011-01, The safety assessment measures of air traffic management for the civil aviation [S]. Beijing: Civil Aviation Administration of China, 2011. (in Chinese) [17]Aeronautical Information Service Center of Bureau of Air Traffic Management of Civil Aviation Administration of China. National aeronautical information publication [S]. Beijing: Air Traffic Management of Civil Aviation Administration of China, 2014. (in Chinese) [18]The Chinese People′s Liberation Army Headquarters. One regulation of flight control [S]. Beijing: The Chinese People′s Liberation Army Headquarters, 2009. (in Chinese) Dr. Wang Shijing is currently a lecture in College of Civil Aviation, Nanjing University of Aeronautics and Astronautics. She received her Ph.D. from College of Civil Aviation, Nanjing University of Aeronautics and Astronautics in 2011. Her main research interests are airspace planning and safety. Ms.Li Qingyun is currently a postgraduate student in College of Civil Aviation, Nanjing University of Aeronautics and Astronautics. Her research interests include airspace planning, air route network planning and traffic engineering. Ms.Cao Xi is currently a postgraduate student in College of Civil Aviation, Nanjing University of Aeronautics and Astronautics. Her research interests include network generated, network optimized and complex network. Ms.Li Haiyun is currently a postgraduate student in College of Civil Aviation, Nanjing University of Aeronautics and Astronautics. Her research interests include network generated, network optimized and complex network. (Executive Editor: Zhang Bei) U8 Document code:A Article ID:1005-1120(2016)04-0469-10 *Corresponding author, E-mail address: shijin_wang@nuaa.edu.cn. How to cite this article: Wang Shijin, Li Qingyun, Cao Xi, et al. Optimization of air route network nodes to avoid ″three areas″ based on an adaptive ant colony algorithm[J]. Trans. Nanjing Univ. Aero. Astro., 2016,33(4):469-478. http://dx.doi.org/10.16356/j.1005-1120.2016.04.469
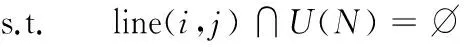
2 Solvement ARNN Optimization Model
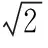
3 Case Study
4 Conclusions
杂志排行
Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- Evolution of Air Traffic Management Concept of Operations and Its Impact on the System Architecture
- A Hybrid Method Combining ImprovedK-means Algorithm with BADA Model for Generating Nominal Flight Profiles
- Flight Schedule Recovery under Uncertain Airport Capacity
- Estimation of Standard Operation Time of Flight Legs Based on Clustering and Probability Analysis
- Effects of Deck Motion and Ship Airwake on Ski-Jump Takeoff Performance of Carrier-Based Aircraft
- A Test Method for the Static/Moving State of Targets Applied to Airport Surface Surveillance MLAT System
