A Hybrid Method Combining ImprovedK-means Algorithm with BADA Model for Generating Nominal Flight Profiles
2016-11-21,,,,
,,,,
1.College of Civil Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, P.R. China; 2.The 28th Research Institute of China Electronic Technology Group Corporation, Nanjing 210007, P.R. China
A Hybrid Method Combining ImprovedK-means Algorithm with BADA Model for Generating Nominal Flight Profiles
TangXinmin1,2*,GuJunwei1,ShenZhiyuan1,ChenPing2,LiBo1
1.College of Civil Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, P.R. China; 2.The 28th Research Institute of China Electronic Technology Group Corporation, Nanjing 210007, P.R. China
(Received 4 November 2015; revised 24 March 2016; accepted 25 April 2016)
A high-precision nominal flight profile, involving controllers′ intentions is critical for 4D trajectory estimation in modern automatic air traffic control systems. We proposed a novel method to effectively improve the accuracy of the nominal flight profile, including the nominal altitude profile and the speed profile. First, considering the characteristics of trajectory data, we developed an improvedK-means algorithm. The approach was to measure the similarity between different altitude profiles by integrating the space warp edit distance algorithm, thereby to acquire several fitted nominal flight altitude profiles. This approach breaks the constraints of traditionalK-means algorithms. Second, to eliminate the influence of meteorological factors, we introduced historical gridded binary data to determine the en-route wind speed and temperature via inverse distance weighted interpolation. Finally, we facilitated the true airspeed determined by speed triangle relationships and the calibrated airspeed determined by aircraft data model to extract a more accurate nominal speed profile from each cluster, therefore we could describe the airspeed profiles above and below the airspeed transition altitude, respectively. Our experimental results showed that the proposed method could obtain a highly accurate nominal flight profile, which reflects the actual aircraft flight status.
air transportation; flight profile;K-means algorithm; space warp edit distance (SWED) algorithm; trajectory prediction
0 Introduction
Airspace resources and air traffic congestion have been rapidly decreasing due to the fast-expanding global aviation industry. Acknowledging this dilemma, the United States and Europe have planned and implemented a next generation air traffic management system, whose core technology is 4D trajectory-based operation[1]. As 4D trajectory prediction with high precision has become critical, its essential issue of mining the nominal flight profile, including intentions of controllers, has also become pivotal. It is necessary to develop a state-of-the-art method to improve the accuracy of the nominal flight profile, so that changes in the aircraft flight status can be predicted in advance and controllers can receive necessary information to handle aircraft conflicts timely.
In recent years, the important role of 4D trajectory prediction in air traffic automation systems has been widely studied. Two types of algorithms are employed for this study: (1) Methods based on an aircraft dynamic model. For example, Coppenbarger developed a method for 4D trajectory prediction based on an aircraft dynamic model in take-off and climbing phases[2]. Gong and Chan proposed a approach that employed a climbing timetable from the flight performance manual to obtain aircraft aerodynamic models and dynamic equations for trajectory estimation[3]. Wu and Guo utilized a numerical integral algorithm and a simplified algebraic algorithm to calculate flight profiles in terminal areas[4]. A kinematics model established on the flight phase can allow trajectory prediction, but the results are not ideal due to the lack of consideration of meteorological factors and performance errors for different aircraft types. (2) Fitting methods based on the center trajectory using data mining technology. For example, Gariel et al. proposed aK-means clustering method based on radar data to monitor aircraft in terms of their actual operation status[5]. For busy areas with many airports, Leiden and Atkins used the clustering method based on grid tracking to analyze different airports, thereby to determine the average trajectories of different aircraft in the arrival and departure phases[6]. Wang and Huang analyzed aircraft flight data using the fuzzy clustering method in the arrival phase and calculated the average center trajectory[7]. However, the methods mentioned above are limited within the data gleaned only from arrival or departure phases rather than the entire flight profile. Therefore, a new concept called the basic flight model was proposed for building horizontal trajectories, altitude profiles, and speed profiles depending on the flight phases, but this method cannot obtain the entire flight profile in an effective manner due to the lack of meteorological factors[8]. Xing et al. proposed a novel method based on aircraft meteorological data relay (AMDAR) data to generate a flight profile, which can obtain the nominal flight altitude profile based on the dynamic space warping algorithm and the speed profile based on a hybrid method that combines the large oval distance algorithm with the base of aircraft data (BADA) model[9-10]. However, AMDAR data have a large sampling interval, so it is not accurate to use the large oval distance between two trajectory points as the aircraft flight distance. Furthermore, the time accuracy of AMDAR data is not adequate, and thus the nominal speed profile includes specific errors.
To determine the actual aircraft flight status, we proposed an improvedK-means algorithm to cluster the altitude profiles of historical trajectory data, thereby to obtain several centers of the flight profiles, i.e., fitted nominal altitude profiles, without relying on the Newtonian mechanics model. Second, we developed a method for integrating the historical meteorological data and speed conversion model based on BADA to obtain the nominal speed profiles. Hence, combining these methods with airway meteorological forecasts could revise the estimated flight trajectory in order to obtain a more accurate 4D trajectory.
1 Generating Nominal Altitude Profiles
1.1 Flight altitude profiles and their characteristics
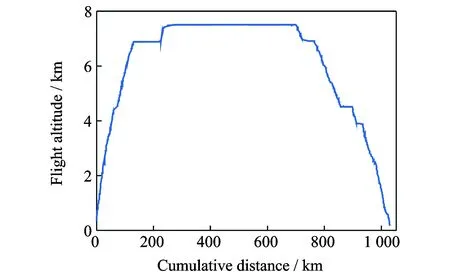
The flight altitude profile is a two-dimensional image that represents the relationship between the flight altitude and range, i.e., the trajectory in the vertical direction of a geographic coordinates system. As shown in Fig.1, a typical flight altitude profile can be divided into three stages:a—drepresents the climbing stage,e—fthe cruise stage, andg—jthe descent stage. The specific flight altitude parameters for each stage were described in Ref.[11].
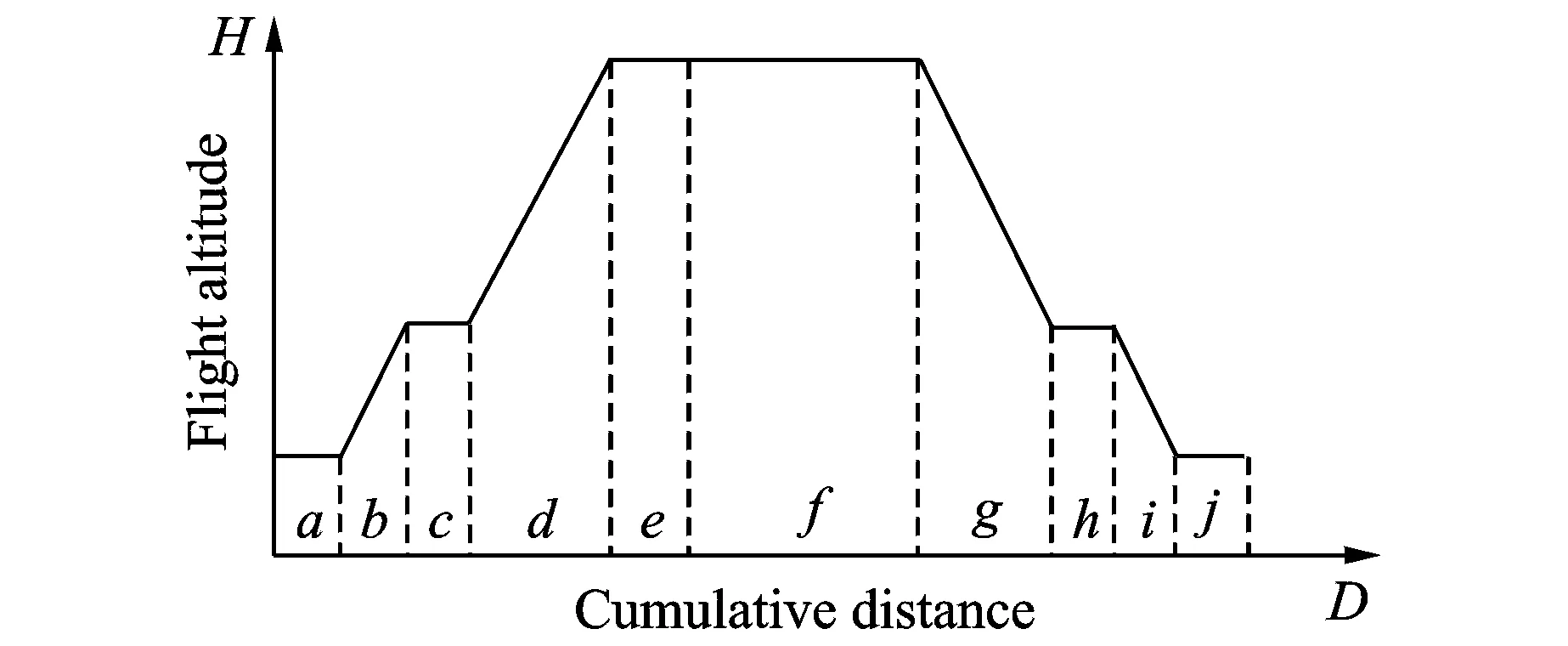
Fig.1 A typical flight altitude profile
1.2 Altitude profile measurment based on SWED
Marteau designed a time warp edit distance algorithm[12]based on the characteristics of historical trajectory data. The method performed better than classic dynamic time warping algorithms[13-14], because it involved the influence of the non-matching cost and distance deviation so as to measure the distance between time sequence trajectories. but it lacked the limitation of a time warping degree. Thus, considering the relationship between the flight altitude and distance, we proposed an improved space warp edit distance (SWED) algorithm to measure the distance between two profile point series. The proposed method constructs a cost function to calculate the influence of non-matching cost and distance deviations.
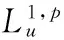
We defined the similarity between any two profile point seriesL1andL2with finite lengths ofpandq, respectively, as
(1)
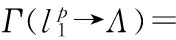
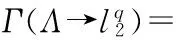
(2)
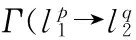
(3)
The rules of the matching and deleting operation are as follows. (1) The editing process is performed from left to right, and ifiis an index on the segments ofL1andjon the segments ofL2, the initial process setting isi=j=1. (2) A matching operation adds one toiandjsimultaneously, which are denoted byi←i+1 andj←j+1. A deletingL1(L2) operation adds one toi(j) only, which is denoted byi←i+1(j←j+1). (3) After segmenti(j) inL1(L2) has been processed using either a matching or a deleting operation, it is impossible for it to be edited again. A recursive algorithm is conducted to complete the overall process therefore to obtain the final global minimum cost function value.
1.3 Clustering and fitting nominal altitude profiles based on an improvedK-means algorithm
TraditionalK-means clustering algorithms set the valuekand initial altitude profile centers randomly, usually leading to the clustering results trapped by local optima[15-16]. In addition, traditional algorithms are no longer applicable to generating cluster centers, given the characteristics of the altitude profile. Therefore, we proposed a nominal altitude profile clustering and fitting method based on an improvedK-means algorithm to obtain thekfitted altitude profile centers in an effective manner. The technical framework of the method is shown in Fig.2.
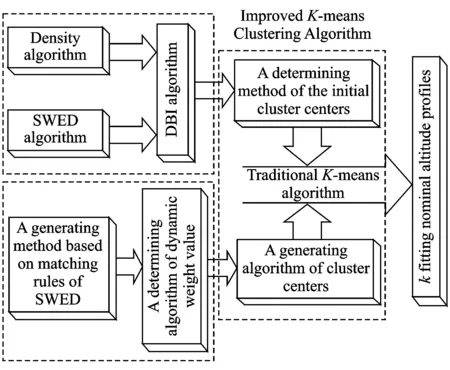
Fig.2 Technical framework of the improved K-means algorithm
In order to determinekinitial altitude profile centers, we proposed a novel concept , i.e., an altitude profile object. For any altitude profile objectLu, if the conditiondswed(Lu,Lv)<ξis met by taking a thresholdξ, then the object number can be defined as the density ofLu. LetM={L1,L2,…,Ln} be the set of altitude profiles and the profile with the maximum density in the setMis regarded as the first initial cluster centerZ1. Then, the second initial centerZ2is determined by seeking the profile farthest fromZ1and the initial altitude profile centerZkis determined as
Zk=Zi:∀j≤n, min{dswed(Zi,Z1),dswed(Zi,Z2),…}≥min{dswed(Zj,Z1),dswed(Zj,Z2),…}
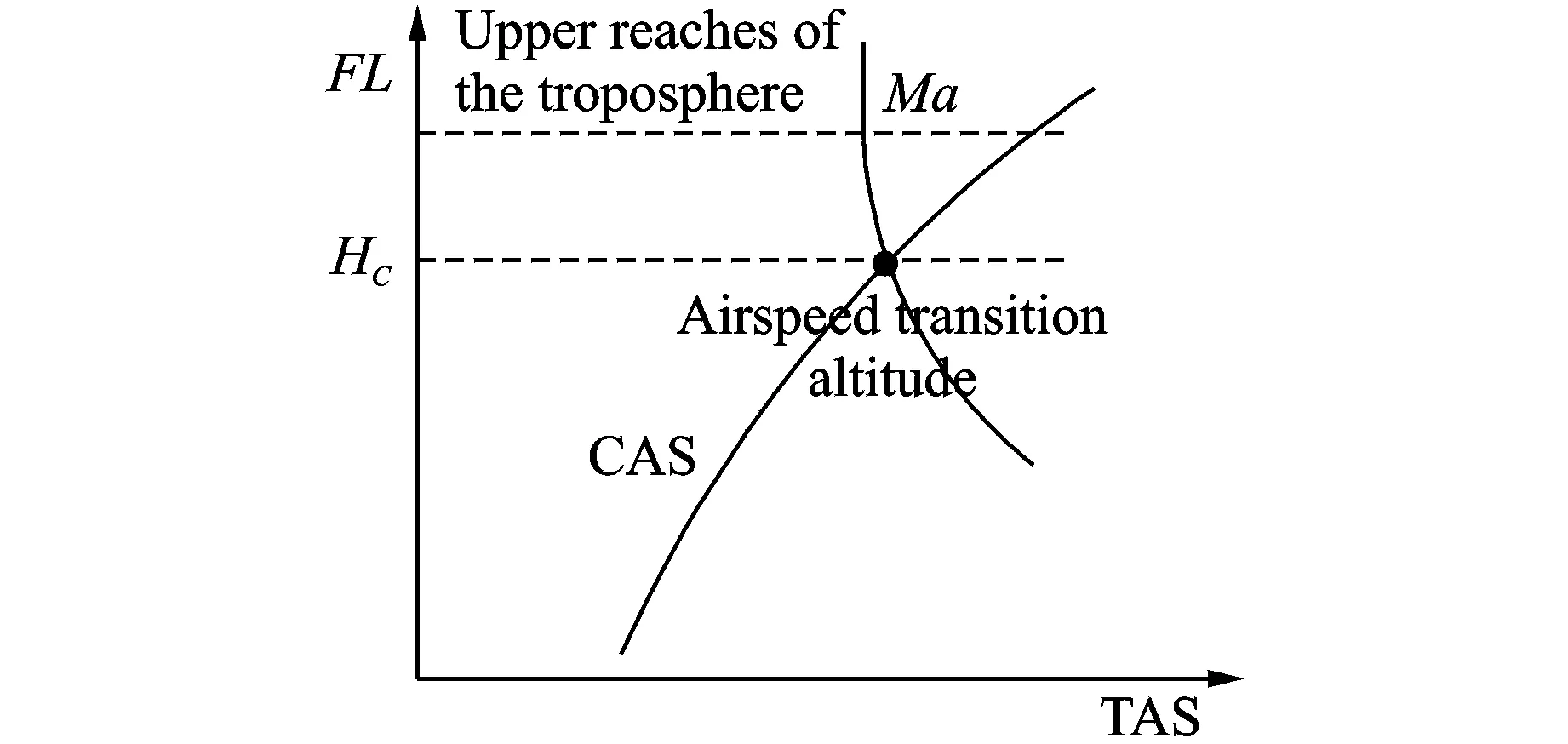
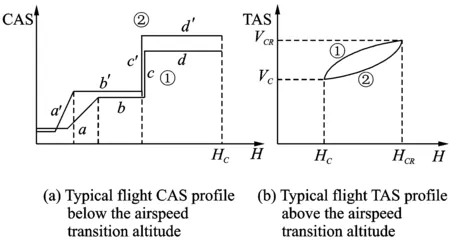
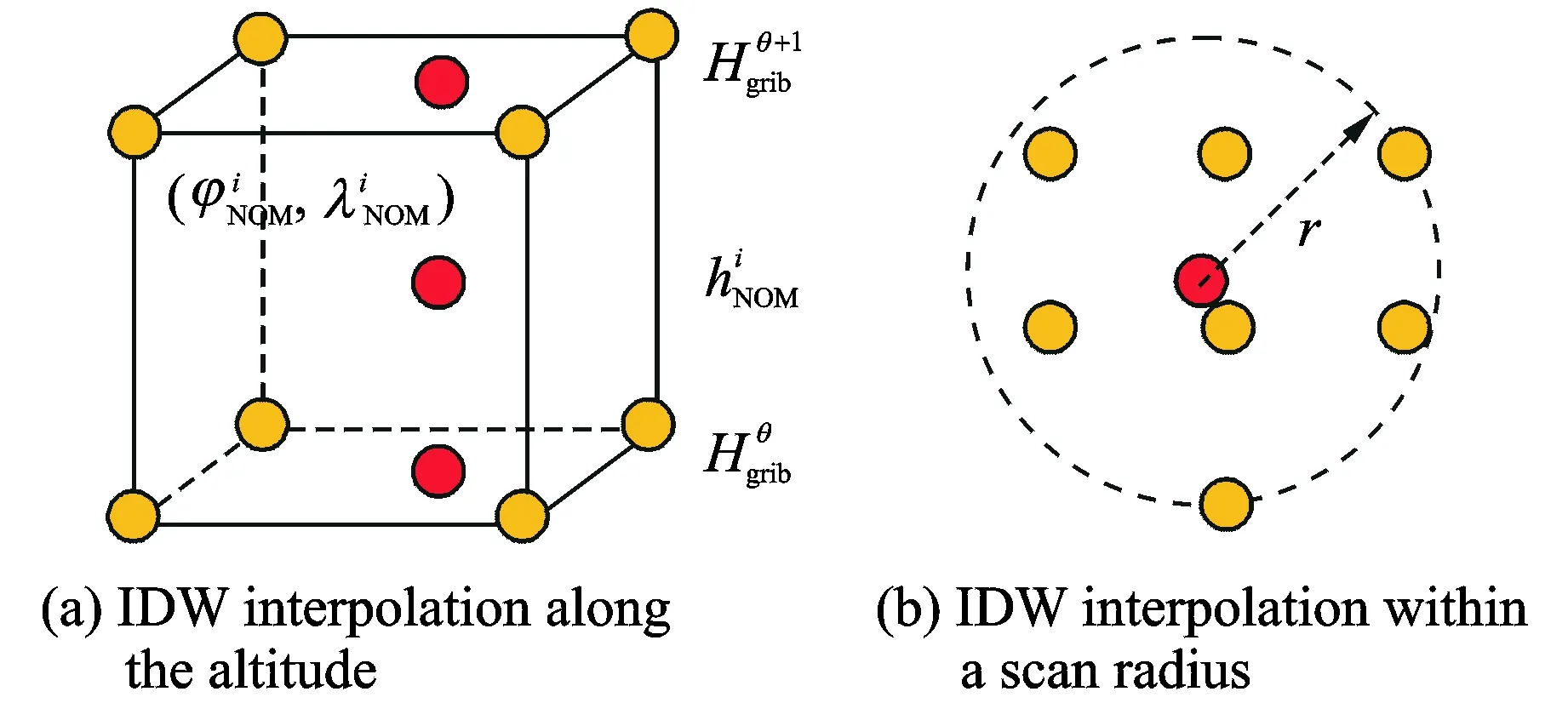
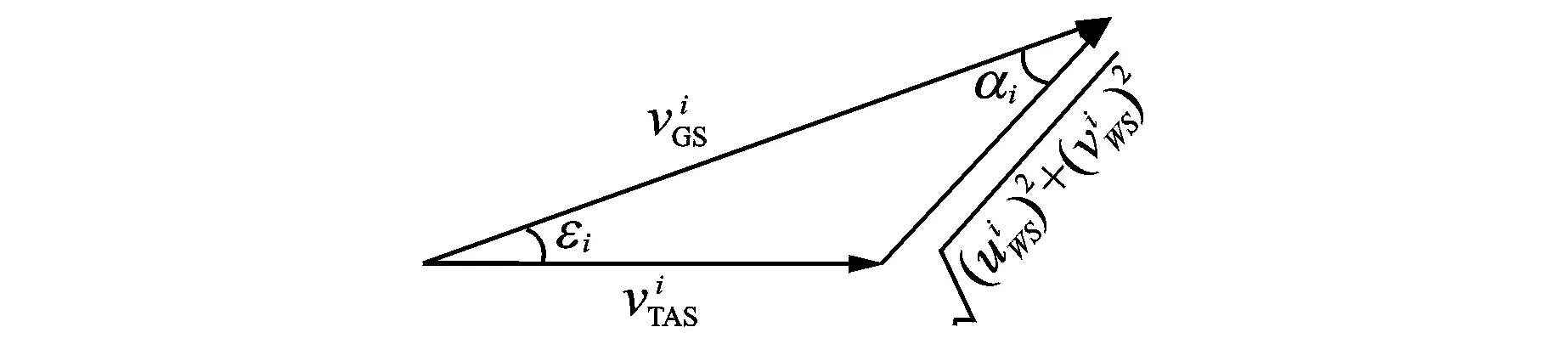
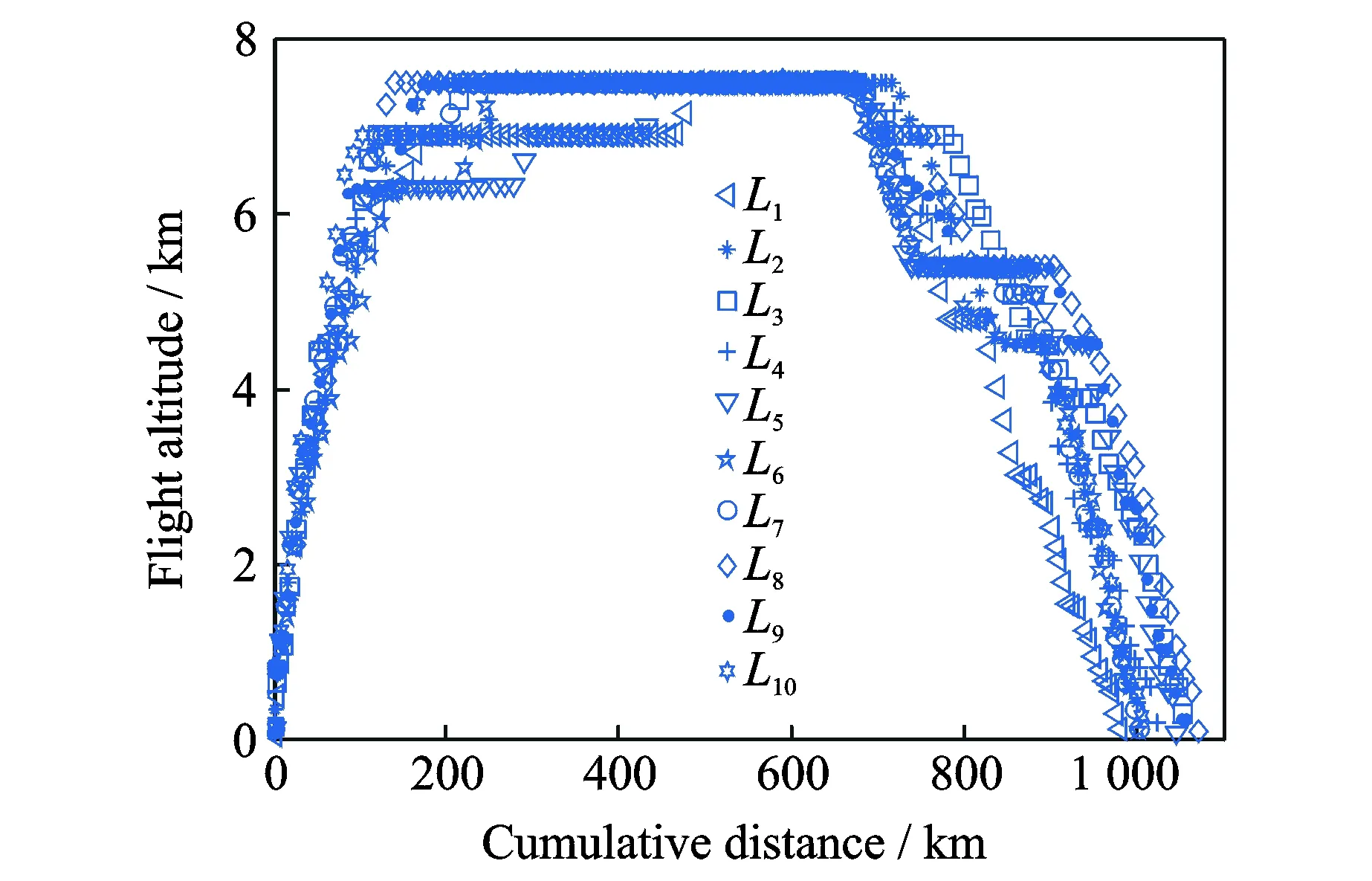
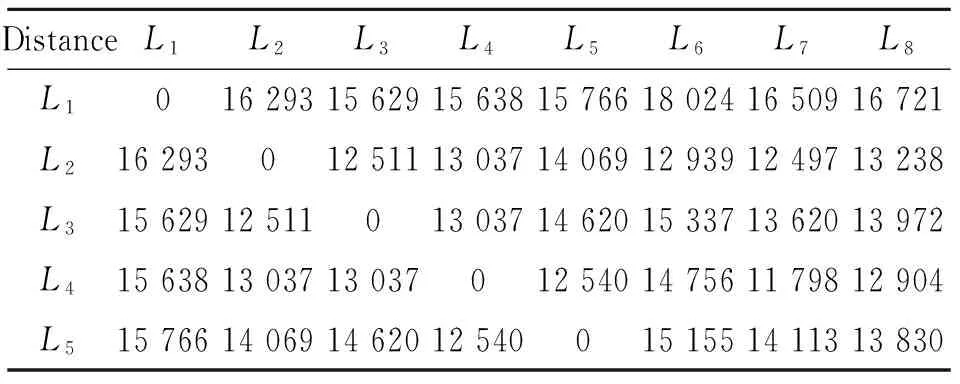
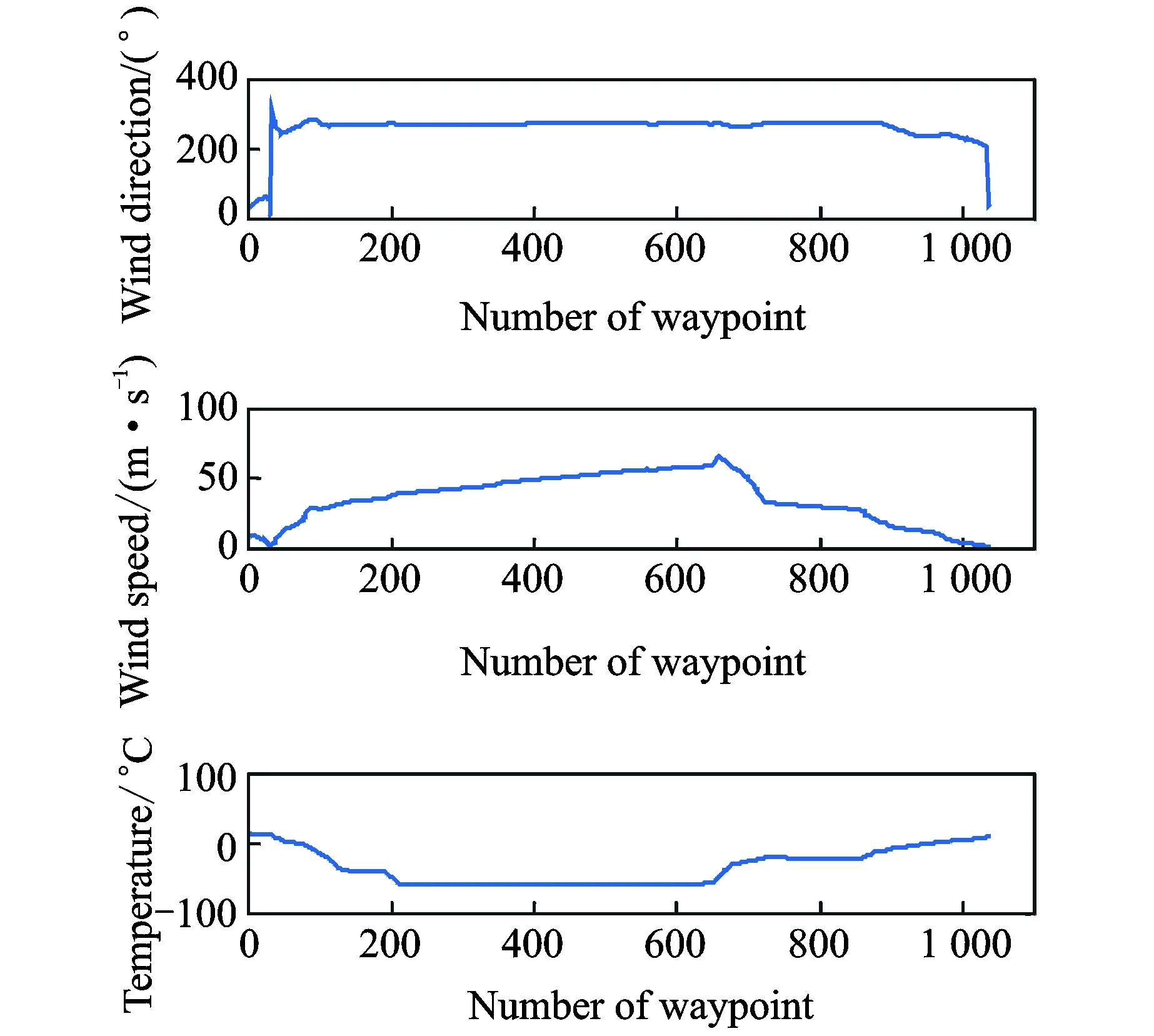
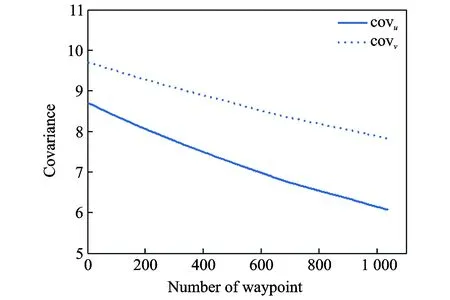
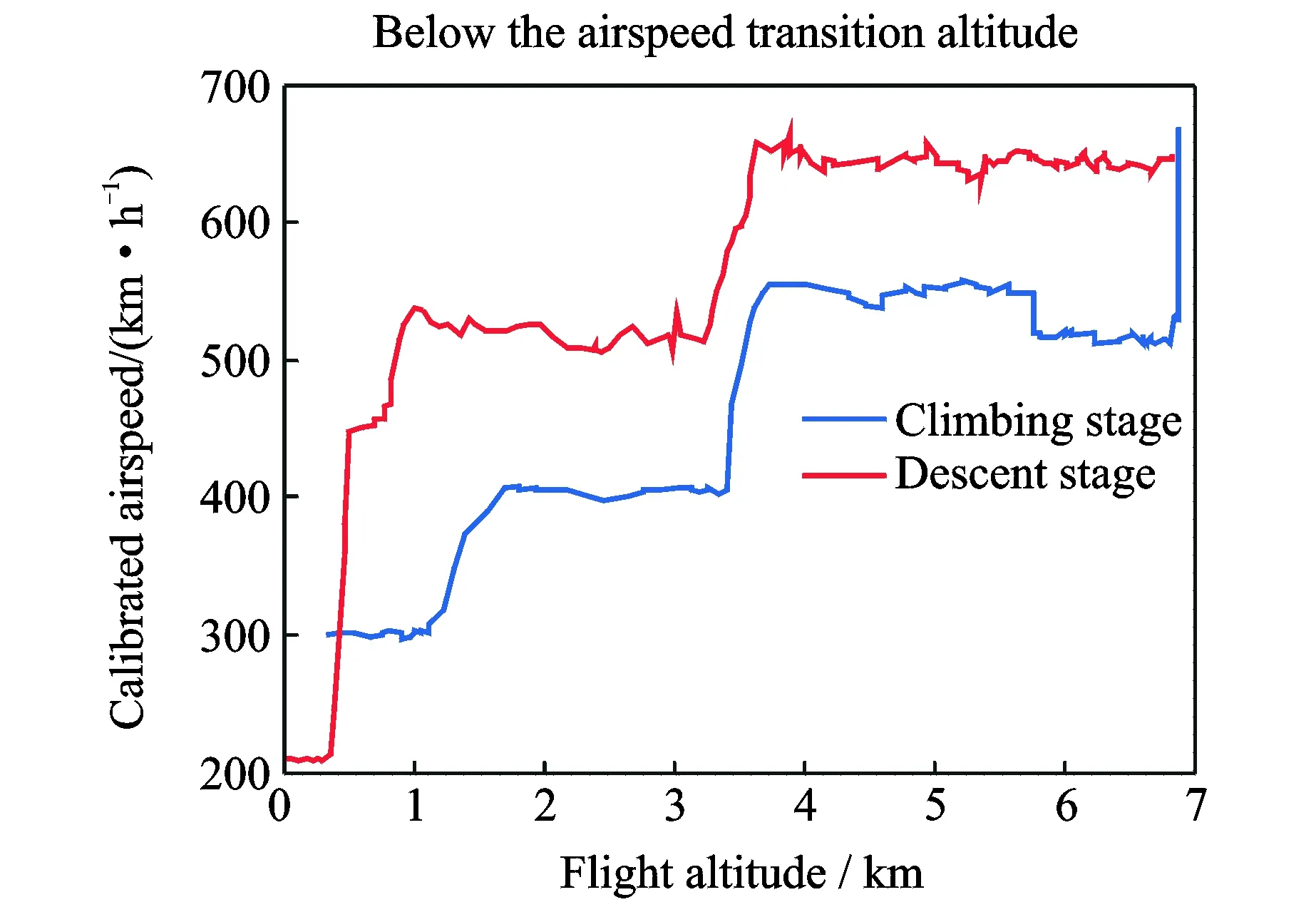
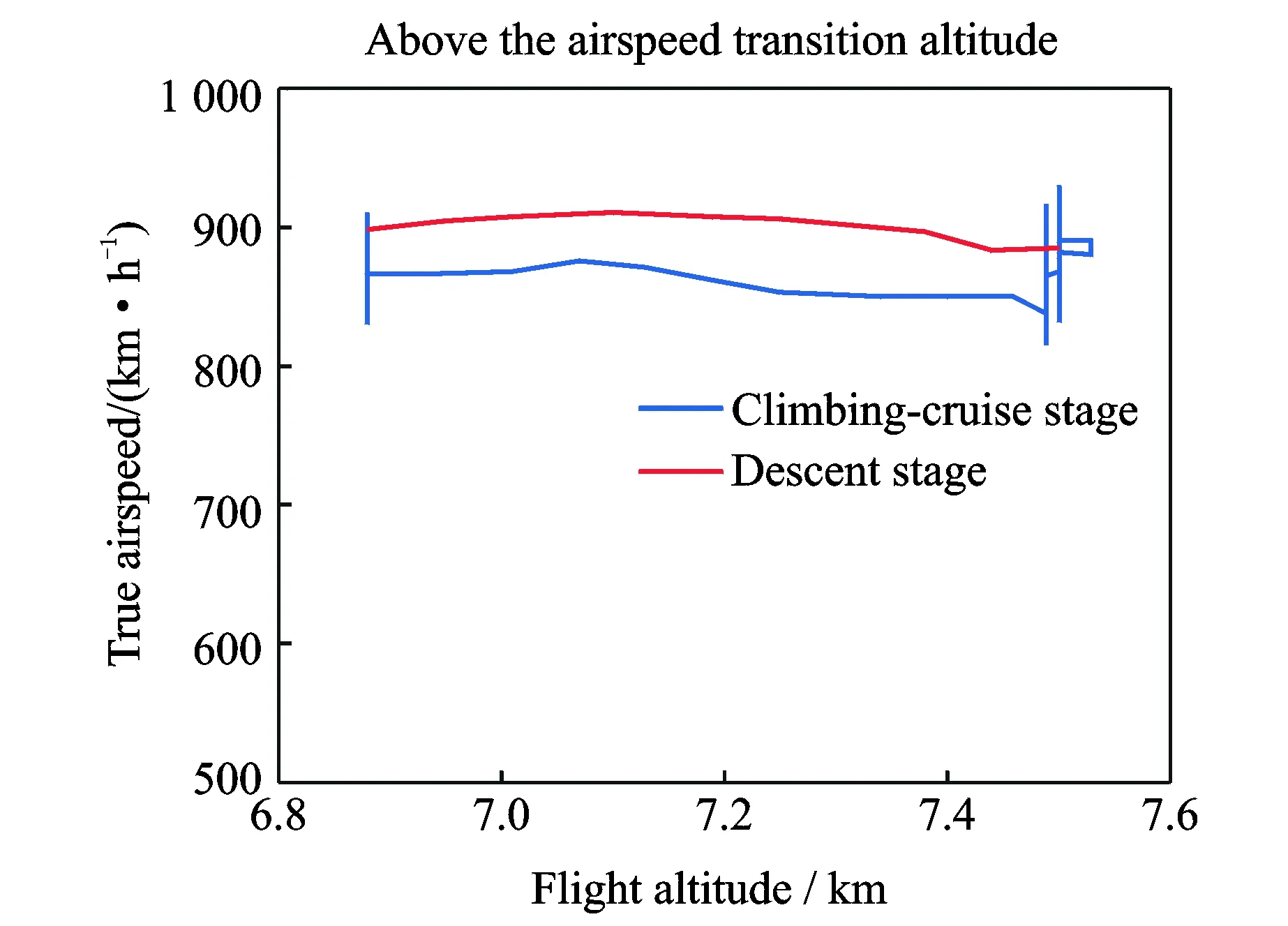
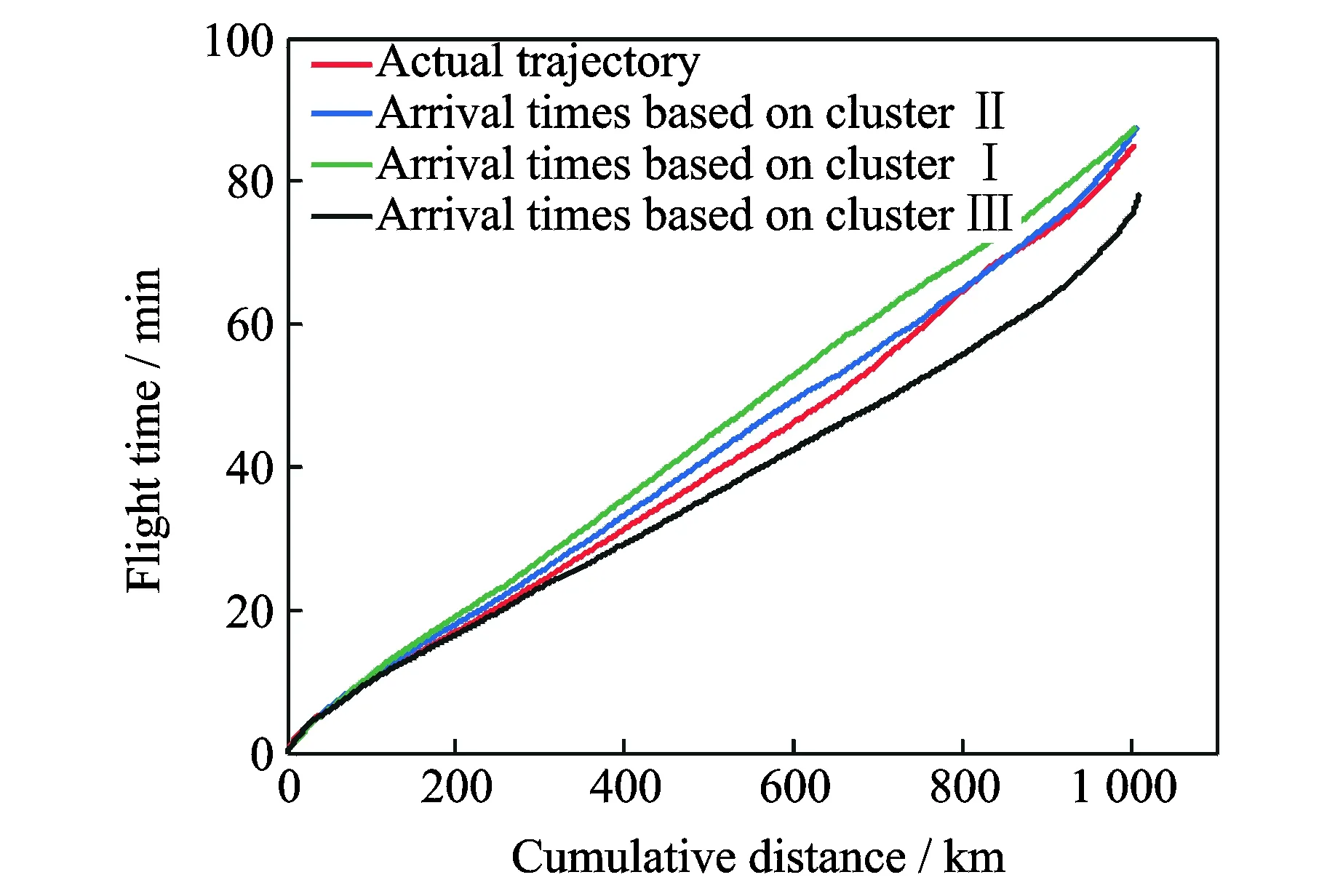
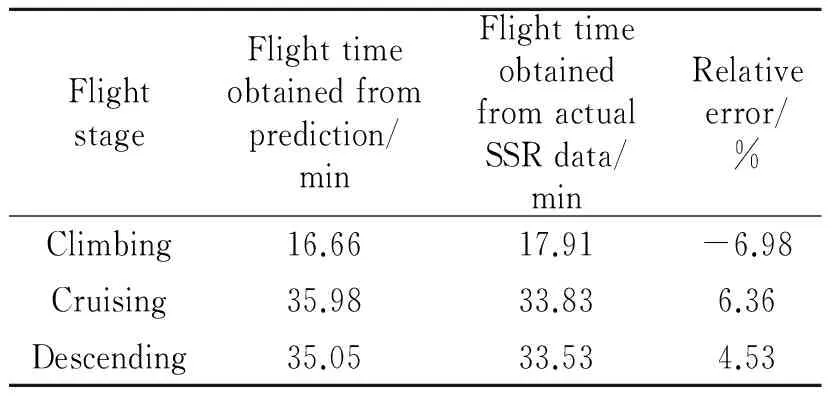
2 (4) Davies-Bouldin index (DBI) is used to synthetically measure the separation degree of the intra-cluster and the condensation degree of inter-clusters. The minimum DBI value, i.e., DBInew>DBIlast, can determine an optimal cluster number. The model equation is summarized as (5) wherekis a cluster number,dswed(Zu,Zv) the distance between the cluster centerZuin clusteruandZvin the clusterv, andSuthe standard error between each trajectory and the cluster centerZuin the clusteru. The method used for determining the cluster center based on the traditionalK-means algorithm cannot be applied to altitude profiles, so we proposed a novel algorithm for generating cluster centers by integrating the weight and matching rules of SWED. The core strategy of the algorithm is to superimpose two arbitrary intra-cluster profiles repeatedly. Assuming thatLNdenotes an altitude profile that is not superimposed in the clusterCkandLlasta center that is superimposed, the algorithm for generating the center between the altitude profilesLNandLlastis as ={ω1(xi,sxi)+ω2(yi,syi)|i∈[1,|Llast|]}= ω1X+ω2Y=Z (6) (7) wheren=|Llast| denotes the length ofLlast, Profile point (xi,sxi) matches with (yi,syi), andia serial number that varies from 1 ton. ω3= (8) In order to obtain the cluster centers for the altitude profile in an effective manner, the dynamic weight is determined based on a regression analysis algorithm to ensure that the generated center is the closest to each intra-cluster profile. The objectSis calculated as (9) whereNrepresents the number of superimposed profiles. The function mentioned above is subject to the following constraints (10) To minimize the value of object S, ω1andω2canbedeterminedbythepartialderivativeoffunctionS,i.e., S′(ω1)=S′(ω2)=0.Finally, kclustersandthefittednominalaltitudeprofilesareobtainedbyapplyingthesuperimpositionstrategyrepeatedly. 2.1 Flight speed profiles and their characteristics A flight speed profile is a two-dimensional image that describes the relationship between speed and altitude during the flight process. Due to changes in the air density and sound velocity with increases in altitude, the calibrated airspeed (CAS), true airspeed (TAS) and Mach number will also change, as shown in Fig.3. Fig.3 Airspeed transition altitude In practice, the airspeed transition altitude written asHCis usually set for convenient flight control. In general, the aircraft operates with constant CAS below the airspeed transition altitude. However, considering the effects of air compressibility, the aircraft flies with a constant Mach number above the airspeed transition altitude. Therefore, according to the airspeed transition altitude, the aircraft flight speed profile is divided into two stages. The phase below the airspeed transition altitude is shown in Fig.4(a). In curve ① of the climbing phase,arepresents the take-off and acceleration stage,bthe climbing stage with constant CAS,cthe acceleration stage at constant altitude, anddthe climbing stage with constant CAS. Similarly, as shown in curve ②, the changing trend in the descending stage is equivalent to the reverse of the climbing stage process. However, considering the relationship between the true airspeed and altitude above the airspeed transition altitude, as shown in Fig.4(b), curve ① is a two-dimensional image describing the relationship between TAS and altitude (transition altitude to cruising altitude), whereas curve ② describes the relationship between TAS and altitude (cruising altitude to transition altitude). Fig.4 A typical flight speed profile In Fig.4,HCR,VCRrepresent the cruising altitude and the cruising speed of aircraft, respectively;VCis the speed at transition altitudeHC. 2.2 Airway meteorological interpolation based on IDW In order to obtain more accurate flight speed profiles, it is necessary to eliminate the influence of meteorological factors on the ground speed. Radar trajectory data do not include airway meteorological data, so gridded binary (GRIB) forecast data gleaned by World Area Forecast System, which are promoted worldwidely by the International Civil Aviation Organization and World Meteorological Organization, are introduced to supply service for aviation. GRIB data with a resolution of 0.5°×0.5° are updated every 6 h, thereby providing meteorological information according to the pressure distribution at 37 levels, with factors such as the air pressure, wind speed, air temperature[17-18]. Therefore, we proposed a data fusion method based on GRIB data and radar data to obtain airway meteorological data via the inverse distance weighted(IDW) interpolation algorithm. (11) (12) The airway meteorological interpolation algorithm is described as following steps. Fig.5 Airway meteorological interpolation principle Aiming at the forecast errors in historical GRIB data, we introduced a method of wind forecast error statistics that can effectively analyze the existential errors[21]. Firstly, the forecast error of the wind is defined as a random field Δw:R×R3→R2where Δw(t,P) denotes the wind at timet∈R and at location pointP(x,y,z)∈R3. For the sake of simplicity, wind in the vertical direction is neglected and the case focuses on where Δw(t,P)∈R2is Gaussian with zero mean and covariance matrixR(t,P,t′,P′)∈R2×2. Assume that the wind-field is isotropic and the east-west wind and south-north wind are uncorrelated. Therefore, according to these hypotheses, the covariance matrix R(t,P,t′,P′) can be simplified as R(t,P,t′,P′)=E[Δw(t,P)·ΔwT(t′,P′)]= (13) whereE[·] represents expected value, and the covariancer(t,P,t′,P′) can be expressed as r(t,P,t′,P′)=σ(z)σ(z′)rt(|t-t′|)· (14) whereσ(z) represents the standard deviation of the wind error at altitudezandAP(z) the atmospheric pressure which can be calculated via using the standard atmosphere model. In addition, according to the reported data in Ref.[22], functionsrt(·),rxy(·),rz(·) all decay exponentially, and can be determined by the parameter values obtained from Ref.[22]. 2.3 Nominal speed profile generation based on BADA model Fig.6 Flight velocity triangle In Fig.6,αiis the wind angle, i.e., the angle between the wind direction with the track line, andεithe drift angle, i.e., the angle of the track line off the course line that can be determined as (15) Then, TAS can be calculated by the resultant vector principle as (16) Base of aircraft data (BADA) is a collection of ASCII files which specifies operation performance parameters, airline procedure parameters and performance summary tables for more than 300 aircraft types, which can be used for trajectory simulation and prediction algorithms within the domain of Air Traffic Management (ATM)[23]. During the BADA modelling process, a variety of aircraft performance reference data is acquired from Aircraft Operation Manuals, Aircraft Performance Engineering Programs, and Jane′s All the World′s Aircraft. The RDAP validation is used to validate the behavior of identified models in respect to real data, including radar data, flight plan data, and meteorology data, which enables identifying all the parameters that describe the BADA aircraft performance model[24]. (17) δi= (18) (19) whereδ=0.223 360 9 represents critical pressure ratio,δ1a pressure ratio, can be calculated by (20) wherea0=340 m/s is the speed of sound under standard atmospheric pressure, and the parametersvCASandMacan be obtained by analyzing the aircraft′s speed profile, where the relationship between the TAS and Mach number can be calculated as (21) 3.1 Simulation In this study, we used 10 radar trajectories from the same flight, i.e., from Xiamen Airport to Wuxi Airport, as an example to discuss their flight profiles. The original relationship between the historical altitude profiles is shown in Fig.7. Fig.7 Original flight altitude profile First, the distance of the two trajectories was calculated using the SWED algorithm, as shown in Table 1. Second, theKinitial cluster centers were determined by integrating the SWED algorithm, density algorithm, and DBI index. Finally, the results of the simulation showed thatL1was an isolated trajectory and whenK=3, DBI was minimized (the changing trend in DBI is shown in Table 2), so we determinedL2,L5, andL10as the initial cluster centers. Table 1 Distance components based on SWED Table 2 Davies-Bouldin index (DBI) We calculated the classification of the altitude profiles using the matching algorithm with SWED and the regression analysis algorithm, as shown in Table 3, where the nominal altitude profile, as shown in Fig. 8, was fitted via cluster II. In addition, the dynamic weight valueω1was optimized as 0.512, 0.659, 0.752, and 0.798 in each case, respectively. Table 3 Classification of the altitude profiles Fig.8 Fitting of the nominal flight altitude profile The meteorological information in the nominal trajectory of cluster II was calculated using the IDW interpolation algorithm, where the radius of the earth was 6 371 km and the two exponent signs were 2 and 1, respectively. The interpolation results are shown in Fig.9. Fig.9 Meteorological diagram based on IDW interpolation In order to discuss the forecast error of GRIB data, the covariance matrix of wind-field forecast errors can be determined by using Eqs.(13)—(14), and the results are displayed in Fig.10, which can meet requirements of interpolation. Fig.10 Covariance of wind-field forecast from the nearest GRIB interpolation point Finally, facilitating the flight speed triangle and CAS/TAS conversion model and the relationship between the aircraft′s speed and altitude, we calculated the airspeed transition altitude as 6 880 m using Eqs.(19)—(21). Figs.11—12 show the nominal airspeed profiles based on the demarcation pointHC, where the flight speed in the cruising stage was maintained at a Mach number of 0.82. Fig.11 Flight CAS profiles below the airspeed transition altitude Fig.12 Flight TAS profiles above the airspeed transition altitude 3.2 Result analysis In order to verify the feasibility of the nominal flight profile, we estimated three trajectories using the flight profiles in clusters I, II, and III for the same flight, where the arrival times at given waypoints were determined and compared with the actual arrival times, which we obtained from SSR or Automatic Dependent Surveillance-Broadcast, as shown in Fig.13. Fig.13 Comparison of flight times based on 4D trajectory prediction Based on this comparison, we found that the arrival times obtained from the flight profiles in cluster II were the closest to the actual flight times, where the total flight time was 2.4 minutes slower than the actual time. In addition, we determined the maximum time error over the cumulative distance of 569.23 km, where the predicted time of arrival was 3.9 minutes later than the actual time. The relative errors in different flight stages are shown in Table 4. Table 4 Flight time in different flight stages Finally, given the condition of a low real-time requirement before take-off, we found that the flight profile obtained by the improved algorithm proposed in this study could satisfy the requirements for trajectory prediction in the future. In order to mine nominal flight profiles containing the intentions of controllers, we proposed an algorithm for generating altitude profiles based on an improvedK-means clustering algorithm and an algorithm for generating speed profiles based on the BADA model using actual aircraft operation characteristics. Taking a flight from Xiamen Airport to Wuxi Airport as an example, we found that this method could reflect the flight intentions of controllers and eliminate the randomness in the trajectory caused by meteorological factors, thereby illustrate the effectiveness of the final results. However, for the generated nominal flight profile, relative errors occurred for two reasons: (1) The airway meteorological data obtained from historical GRIB data using interpolation algorithm were not very accurate due to long refreshing cycle of the GRIB data. (2) During the actual aircraft operation, flight conflict resolution using various strategies, such as adjusting the airspeed and altitude, was considered in order to guarantee the flight safety, which influenced the accuracy of the 4D trajectory estimation compared with that obtained without considering conflicts. In future research, we will focus on developing an airway meteorological revision model to amend the flight profile by improving the precision of airway meteorological data, as well as a strategic conflict-free 4D trajectory planning method for aircraft to guarantee flight safety, thereby obtaining more accurate 4D trajectory estimation. Acknowledgements This research was supported by the National Natural Science Foundation of China (Nos.61174180, U1433125), the Jiangsu Province Science Foundation (No.BK20141413), and the Chinese Postdoctoral Science Foundation (No.2014M550291). [1] HARRY S, RICHARD B, MICHAEL L. Next generation air transportation system (NGATS) air traffic management (ATM)—airspace project[R]. USA: NASA,2006:25-28. [2] COPPENBARGER R A. Climb trajectory prediction enhancement using airline flight planning information[C]∥Proceedings of the AIAA Guidance, Navigation, and Control Conference. Portand: AIAA, 1999:1077-1087. [3] GONG C, CHAN W N. Using flight manual data to derive aero-propulsive models for predicting aircraft trajectories[C]∥AIAA Aircraft Technology, Integration, and Operations (ATIO) 2002 Technical. California: AIAA, 2002:1-7. [4] WU Shufan, GUO Suofeng. Synthesis of aircraft vertical flight profile based on four-dimensional guidance in terminal airspace[J]. ACTA Aeronautical ET Astronautical Sinica,1993,14(5):261-268. (in Chinese) [5] GARIEL M, SRIVASTAVA A N, FERON E. Trajectory clustering and an application to airspace monitoring[J]. IEEE Transactions on Intelligent Transportation Systems, 2011,12(4):1511-1524. [6] LEIDEN K, ATKINS S. Trajectory clustering for metroplex operations [C]∥Proceedings of 11th AIAA Aviation Technology, Integration, and Operation (ATIO) Conference. USA: AIAA, 2011:7066. [7] WANG Taobo, HUANG Baojun, Application of improved fuzzy clustering algorithm to analysis of trajectory[J]. China Safety Science Journal, 2013,31(6):38-42. (in Chinese) [8] WANG Chao, GUO JiuXia, SHEN Zhiping. Prediction of 4D trajectory based on basic flight models[J]. Journal of Southwest Jiaotong University, 2009,44(2):295-300. (in Chinese) [9] XING Jian, TANG Xinmin, Han Songchen, et al. Method for generating flight profile based on AMDAR data[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2015,47(1):64-70. (in Chinese) [10]TANG X M, XING J, CHEN P. Generating nominal flight profile for air traffic control system based on AMDAR data[C]∥2014 IEEE 17th International Conference on Intelligent Transportation Systems (ITSC). USA: IEEE, 2014:2644-2649. [11]DING Songbin. Flight performance and flight plan[M]. Beijing: Science Press, 2013. (in Chinese) [12]MARTEAU P F. Time warp edit distance with stiffness adjustment for time series matching[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence archive, 2009,31(2):306-318. [13]KEOGH E, RATANAMAHATANA C A. Exact indexing of dynamic time warping [J]. Knowledge and Information System, 2005:358-368. [14]CHEN Q, HU G Y, GU F L, et al. Learning optimal warping window size of DTW for time series classification[C]∥The 11th International Conference on Information Sciences, Signal Processing and their Applications, Special Sessions. [S.l.]:[s.n.],2012:1272-1277. [15]WANG S Y. An improved K-means clustering algorithm based on dissimilarity[C]∥2013 International Conference on Mechatronic Sciences, Electric Engineering and Computer (MEC). Shenyang, China: IEEE, 2013:20-22. [16]MEHAR A M, MATAWIE K, MAEDER A. Determining an optimal value ofKinK-means clustering [C]∥2013 IEEE International Conference on Bioinformatics and Biomedicine. USA: IEEE, 2013:52-55. [17] SÖKMEN N. GRIB message resolution and accuracy analysis of upper-level wind[J]. Air Traffic Management, 2010, 190(1):51-63. [18]WU Xiaoguang, ZHANG Junfeng, JIANG Haixiang. Application of GRIB data for 4D trajectory prediction[J]. Aeronautical Computing Technique, 2013,43(6):59-62. (in Chinese) [19]EMRE O, SERDAR B, USTUNDAG B B, et al. Land surface temperature-based spatial interpolation using a modified inverse distance weighting method[C]∥2013 Second International Conference on Agro-Geoinformatics (Agro-Geoinformatics). [S.l.]:[s.n.],2013:110-115. [20]DONG Zhinan, ZHEN shuanning, ZHAO Huibing. Comparative analysis of wind field simulation method based on spatial interpolation[J]. Journal of Geo-information Science, 2015,17(1):37-44. (in Chinese) [21]LYMPEROPOULOS I, LYGEROS J. Sequential Monte Carlo methods for multi-aircraft trajectory prediction in air traffic management[J]. International Journal of Adaptive Control & Signal Processing, 2010,24(10):830-849. [22]COLE R E, RICHARD C, KIM S, et al. An assessment of the 60 km rapid update cycle (RUC) with near real-time aircraft reports[R]. USA: NASA/A-1, MIT Lincoln Laboratory, 1998. [23]EURO-CONTROL Experimental Centre. User Manual for the Base of Aircraft Data[R]. Germany: [s.n.], 2010. [24]EURO-CONTROL Experimental Centre. Base of aircraft data (BADA) aircraft performance modelling report[R]. Germany: [s.n.], 2009. Prof. Tang Xinmin is currently a professor of College of Civil Aviation in Nanjing University of Aeronautics and Astronautics. His research interests include (1) Petri Net and Discrete Event Dynamic System theory; (2) Hybrid System Theory. (3) Intelligent Air Traffic System. Mr. Gu Junwei is currently a postgraduate of College of Civil Aviation in Nanjing University of Aeronautics and Astronautics. His research interest is next-generation Air Traffic Control Automation System. Dr. Shen Zhiyuan is currently an assistant professor of college of civil aviation at Nanjing University of Aeronautics and Astronautics (NUAA). His research interests include ADS-B technique, 4D trajectory prediction. Mr. Chen Ping is currently a chief expert in the 28th Research Institute of China Electronic Technology Group Corporation, and academic leader in the National Air Traffic Control Engineering Center. His research interests include (1) Airspace Management; (2) Traffic Management; (3) Data Fusion Disposal; (4) Intelligent Aid Decision Making System. Mr. Li Bo is currently a graduate of College of Civil Aviation in Nanjing University of Aeronautics and Astronautics. His research interest is Low Airspace Air Traffic Management. (Executive Editor: Zhang Bei) V355 Document code:A Article ID:1005-1120(2016)04-0414-11 *Corresponding author, E-mail address: tangxinmin@nuaa.edu.cn. How to cite this article: Tang Xinmin, Gu Junwei, Shen Zhiyuan, et al. A hybrid method combining improvedK-means algorithm with BADA model for generating nominal flight profiles[J]. Trans. Nanjing Univ. Aero. Astro., 2016,33(4):414-424. http://dx.doi.org/10.16356/j.1005-1120.2016.04.414
2 Nominal Speed Profile Generation
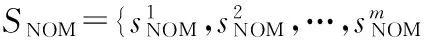
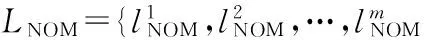
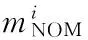

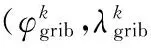
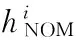
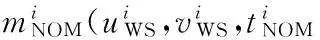
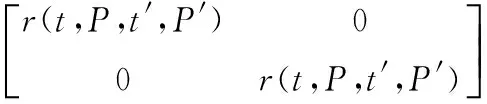
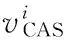

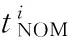
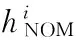
3 Simulation and Discussion


4 Conclusions
杂志排行
Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- Evolution of Air Traffic Management Concept of Operations and Its Impact on the System Architecture
- Optimization of Air Route Network Nodes to Avoid ″Three Areas″ Based on An Adaptive Ant Colony Algorithm
- Flight Schedule Recovery under Uncertain Airport Capacity
- Estimation of Standard Operation Time of Flight Legs Based on Clustering and Probability Analysis
- Effects of Deck Motion and Ship Airwake on Ski-Jump Takeoff Performance of Carrier-Based Aircraft
- A Test Method for the Static/Moving State of Targets Applied to Airport Surface Surveillance MLAT System
