一类欧式期权定价问题

荆卉婷

一类欧式期权定价问题

荆卉婷

赋权分数布朗运动因具备长程相依性、重对数率等精美性质，可用于资本市场。文章主要考虑由赋权分数布朗运动驱动的金融市场，从其相关性质出发，定义了新型的欧式期权定价公式并绘制出一些仿真结果。

赋权分数布朗运动；欧式期权

一、前言

具有长程相依性的自相似随机过程广泛应用于包括金融、电信学、流体力学 等许多领域。分数布朗运动(fractional Brownian motion)是使用最广泛的一种，也是自相似高斯过程中唯一一个具有平稳增量的随机过程。近年来，分数布朗运动以其简单的结构、精美的性质以及广泛的应用引起了许多学者的兴趣，随着研究的不断深入，已经获得了很多有意义的结果但是与分数布朗运动的广泛研究相比较，其它类型的自相似高斯过程的研究却非常少！这主要是由于其他类型自相似高斯过程并没有平稳增量，且相依结构更为复杂。

此后，很多学者开始了诸如次分数布朗运动，双分数布朗运动等自相似高斯过程的研究，然而对于赋权分数布朗运动的研究还非常少，结构也更加复杂，这也是我们开展赋权分数布朗运动研究的原因之一。另一方面，赋权分数布朗运动涵盖分数布朗运动、双分数布朗运动等许多具有长程相依性的自相似高斯过程，所以我们认为这类研究对于金融市场的定价问题具有应用意义。

本文主要研究赋权分数布朗运动在金融市场中的一个应用，给出了由赋权分数布朗运动版本的欧式期权定价公式，并绘出了当长程相依性指数及波动率取不同值时，欧式期权的价格随时间变化的图像。

二、欧式期权定价公式及相关证明

由于金融系统的复杂性，投资者往往不是在得到金融信息时立刻做出决定，而是等信息达到一定的量的时候再做出决定。这种行为往往导致长程相依性，赋权分数布朗运动能够成为解释这种现象的有用工具。在我们的模型中，假设股票价格V服从下面的随机过程：

假设金融市场有两种资产，其中一种资产为证券，收益率为无风险利率r;另一种资产为股票，其收益率是一个随机过程Vt，初始价格为V0。我们关心的是以此股票为标的资产的到期日为T执行价格为k的欧式期权定价问题。

定义1：股票价格{Vt}的预期收益μ与时间T之间满足

因为对{Vt}没有限制，μ一般情况下与T有关。

引理1：欧式看涨期权价格C(K,T)为

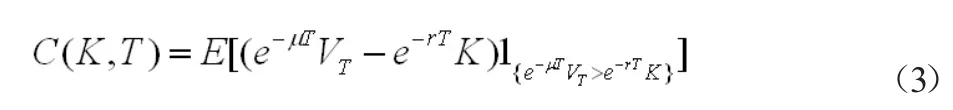
类似的，欧式看跌期权价格P(K,T)为

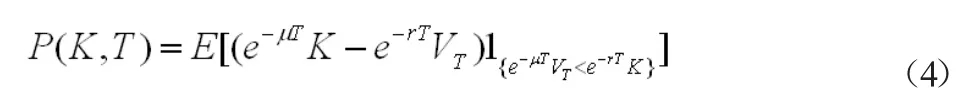
因此我们有

引理2：方程（1）的解为

定理1.到期日为T执行价格为K的欧式看涨期权价格C(K,T)为

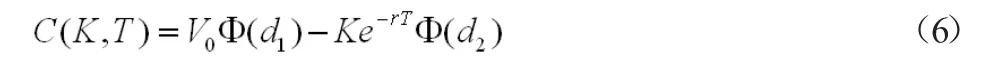
其中

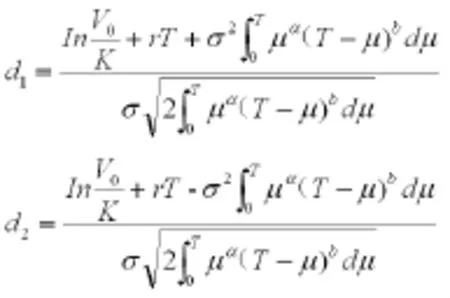
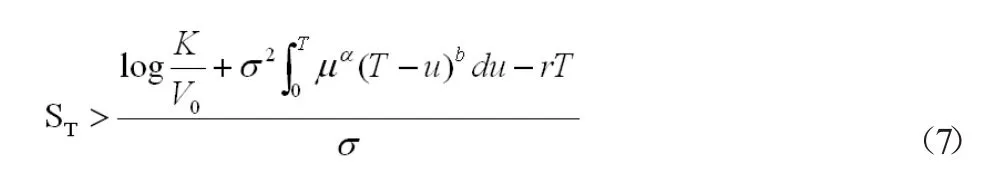
又根据引理（1）（2），可知到期日执行价格为的欧式期权价格C（K,T）为

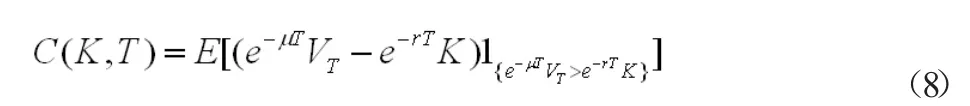
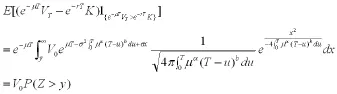
另一方面，我们可以类似证明.

三、数值仿真

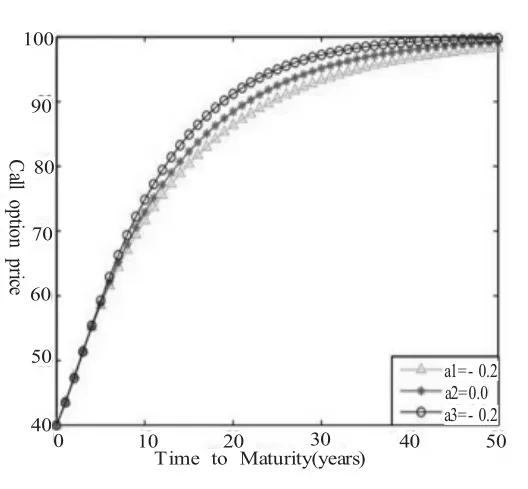
根据以上内容，给出一些数值仿真结果，在图（1）～图（4）中，我们绘出了不同参数值σ∈{0.2，0.3,0.5}从图可以看出，看涨期权的价格是到期日T，波动率σ及长相依指数α的增函数；看跌期权的价格是波动率σ及及长相依指数α的增函数，但关于到期日T是先增后减。取σ∈{0.2，0.0，0.2}固定b=0.4的图像

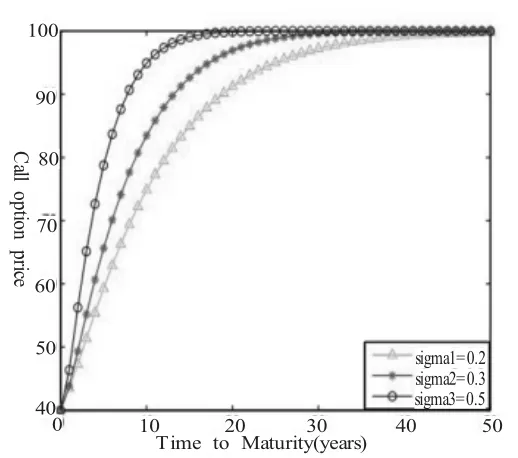
图（1）

图（2）

图（1）：期权价格关于到期日为T的图像，其中的参数值为r=0.06，α=0.2，b=0.4，K=60，V0=100,0＜T＜50.

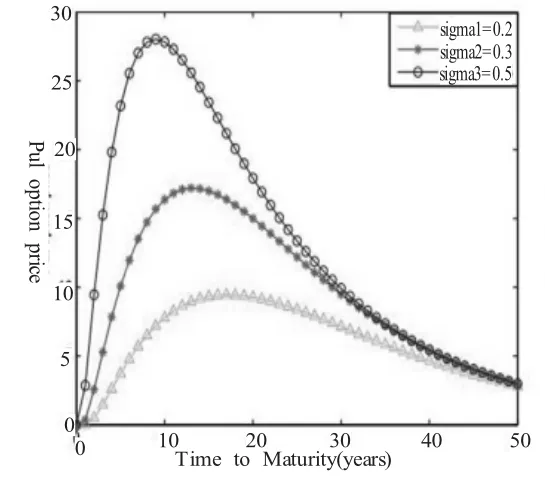
图（2）：期权价格关于到期日为T的图像，其中的参数值为b=0.4， r=0.06，σ=0.2，K=60，V0=100,0＜T＜50.K=60，V0=100,0＜T＜50.

图（3）

图（4）

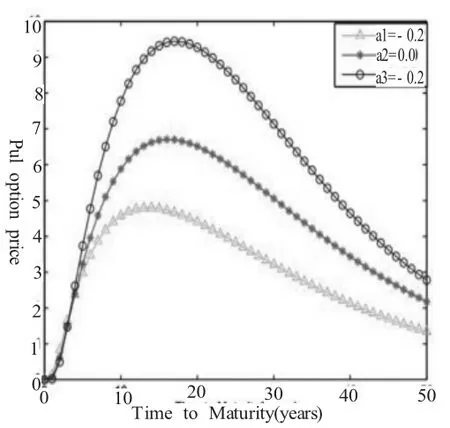
图（3）:长程相依指数取不同参数值时欧式看涨（看跌）期权价格关于到期日T的图像，其中的参数数值为r=0.06，α=0.2，b=0.4，K=60，V0=100,0＜T＜50.

图4：长程相依指数取不同参数值时欧式看涨（看跌）期权价格关于到期日T的图像，其中的参数数值为b=0.4，r=0.06，σ=0. 2，K=60，V0=100,0＜T＜50.K=60，V0=100,0＜T＜50.

四、总结

本文利用赋权分数布朗运动的一些良好的性质与实际金融市场相结合，建立了依托该理论的数学公式，试利用其特质给出欧式期权的定价公式，并绘制了仿真图像，发现赋权分数布朗运动，确实可应用于金融市场，尤其是在信用违约率、期权定价等方面拥有广泛应用，因此未来进行更优化处理会得到更准确的结论，并且非常具有实用价值。

[1]E.Al′os,O.Mazet and D.Nualart,Stochastic calculus with respect to Gaussian processes,Ann.Prob.29(2001),766-801.

[2]L.An and L.Yan,Smoothness for the collision local time of fractional Brownian motion,Preprint,2011.

[3]Yan L,Yang X.Some Remarks on Local Time-Space Calculus. Stat Prob Lett,2007,77:1600-1607.

[4]安磊.赋权分数布朗运动的轨道分析[D].东华大学，2011.

荆卉婷，女，黑龙江佳木斯人，宁波工程学院经济与管理学院助教、硕士，研究方向：金融工程。

F830.91

A

1008-4428（2016）06-79-02