尾缘锯齿结构对叶片边界层不稳定噪声的影响

陈伟杰， 乔渭阳， 仝帆， 段文华， 刘团结

西北工业大学 动力与能源学院， 西安 710129

尾缘锯齿结构对叶片边界层不稳定噪声的影响

陈伟杰， 乔渭阳*， 仝帆， 段文华， 刘团结

西北工业大学 动力与能源学院， 西安 710129

实验研究了不同雷诺数(2×105～8×105)、不同攻角状态下，3种相同波长(4%弦长)不同振幅(分别为5%、10%、15%弦长)尾缘锯齿结构对叶片层流边界层不稳定噪声的影响。研究表明，在0°攻角状态下，尾缘锯齿会增强甚至诱导产生新的不稳定噪声，显著增大叶片自噪声；在大攻角状态下，尾缘锯齿会减弱甚至完全抑制不稳定噪声，降噪量高达40 dB，降噪机制在于尾缘锯齿结构破坏了不稳定噪声产生所需的声学反馈回路。尾缘锯齿会降低不稳定噪声频率，且锯齿振幅越大，不稳定噪声频率越低。

尾缘锯齿； 层流边界层； 不稳定噪声； 声学反馈回路； T-S波

当来流湍流度较弱时，叶片前缘干涉噪声较小，尾缘自噪声占主导作用。目前尾缘自噪声问题已获得广泛研究，Howe[1]对尾缘噪声理论模型进行了综述，Brooks等[2]实验研究了NACA0012翼型尾缘自噪声，其将翼型尾缘自噪声分为5类，并给出了尾缘噪声半经验预测模型。Paterson等[3]首次对层流边界层不稳定噪声进行了系统的实验研究，将其称为涡脱落噪声，发现了单音频率随速度变化的“阶梯形”结构。Tam[4]否定了Paterson的“涡脱落模型”，首次提出了介于振荡尾迹与叶片尾缘之间的“声学反馈回路模型”，解释了Paterson实验中发现的“阶梯形”结构。此后，许多研究者采用热线风速仪、粒子图像测速仪、激光多普勒测速仪、线性稳定性理论和直接数值模拟等手段对此问题进行了研究。Arbey和Bataille[5]提出了与Tam不同的声学反馈回路，其认为反馈回路介于叶片尾缘与上游最大速度点之间。许多研究表明，边界层不稳定噪声的产生主要与叶片压力面尾缘附近的流动分离相关，而与吸力面的边界层流动无关[6-10]。Desquesnes等[11]提出了不同的看法，其认为不稳定噪声的产生与压力面、吸力面的边界层流动均有关，压力面为主要的反馈回路，吸力面为二次反馈回路。Arcondoulis等[12]对不同的声学反馈回路进行了总结，并提出了亟待解决的问题。

声学反馈回路包含4个部分：层流边界层不稳定性诱导产生Tollmein-Schlicting(T-S)波；T-S 波向下游传播，经过边界层分离区时被放大；经过放大的T-S波在叶片尾缘散射为声波；声波向上游传播，通过边界层感受性增强T-S波，完成一个循环。由此可见，破坏反馈回路中的任一部分均可以减弱甚至抑制边界层不稳定噪声。Inasawa等[13]研究了等离子体对NACA0012翼型边界层不稳定噪声的影响，研究表明，等离子体控制器可以有效降低不稳定噪声。Howe[14-15]从理论上推导了尾缘锯齿的降噪效果，但必须指出，Howe的理论模型主要针对叶片湍流边界层噪声，不适用于本文所要讨论的层流边界层不稳定噪声。此后，尾缘锯齿结构获得了广泛的研究，并被证明是一种有效降低湍流边界层噪声的构型[16-18]，但关于其对层流边界层不稳定噪声的影响研究较少。

本文采用实验手段研究低湍流度不同雷诺数、不同攻角条件下叶片层流边界层不稳定噪声，分析不稳定单音噪声频率和幅值与来流速度及攻角的关系，探索尾缘锯齿结构的降噪效果及降噪规律以及其对不稳定单音噪声频率的影响。

1 实验装置及测量方法

1.1 全消声室

本实验在中国飞机强度研究所航空噪声与动强度航空科技重点实验室进行，全消声室尺寸为6 m×4 m×6 m，风洞出口为240 mm×300 mm的矩形，最高速度可达100 m/s，风洞出口湍流度小于1%，如图1(a)所示。叶片竖直安装，上下端壁通过有机玻璃板夹持，为便于安装叶片，在风洞出口搭架了桁架，采用吸声棉包裹桁架以减弱桁架对声场的影响。通过分析背景噪声可知，桁架对声场的影响较小。

图1 全消声室实验装置Fig.1 Anechoic chamber experiment set-up

远场指向性测量传声器布置方案如图1(b)所示，采用25路传声器，测量角度范围为30°～150°，间隔5°，传声器位于距离叶片半展长半弦长点1.5 m的圆环上，U0为来流速度，R为测量半径。如无特殊说明，本文所给声压级频谱为90°方位角频谱。

1.2 尾缘锯齿叶片

实验对象包括4种叶片：基准叶片和3种尾缘锯齿叶片，叶片弦长c=150 mm，展长为300 mm。尾缘锯齿结构如图2所示，衡量锯齿结构的参数为锯齿振幅2h和锯齿波长λ，锯齿结构设计参数如表1所示，其中H=2h为锯齿振幅,表中H5λ4表示锯齿振幅为5%弦长、锯齿波长为4%弦长，利用振幅、波长两个参数组合表示不同的锯齿结构，其他类似。实物图参见图3，叶片由铝合金机械加工而成，尾缘锯齿在基准叶片上线切割而成，在叶片20%及80%弦长位置处加工螺纹孔以便将叶片安装于有机玻璃板，有机玻璃板上打有通孔用来改变叶片攻角。

图2 尾缘锯齿叶片结构示意图Fig.2 Sketch of blade with trailing edge serrations

表1 尾缘锯齿结构设计参数Table 1 Design parameters of trailing edge serrations

ConfigurationLabelλ/HNACA0012BaselineWithnoserrationH=0.05c,λ=0.04cH5λ40.80H=0.10c,λ=0.04cH10λ40.40H=0.15c,λ=0.04cH15λ40.27

图3 尾缘锯齿叶片Fig.3 Blade with trailing edge serrations

1.3 实验状态及测量设备

实验中来流速度为20～80 m/s，对应的基于叶片弦长的雷诺数Re=2×105～8×105，几何攻角变化范围为α=0°～15°。实验室条件下有限的风洞出口尺寸会造成来流流线弯曲和下洗，导致有效攻角减小，Brooks等[19]基于升力面理论给出了如下攻角修正公式：

αe=αg/ζ

(1)

(2)

(3)

式中：αg为几何攻角；αe为有效攻角；L为风洞宽度。采用式(1)～式(3)对攻角进行修正，结果如表2所示。

本实验采用BSWA公司1/4英寸预极化自由场传声器，其有效频率范围为20～20 000 kHz，最大可测量168 dB的声压信号，工作温度范围为-50～110 ℃，环境温度系数为0.01 dB/K，环境

表2 攻角修正Table 2 Correction of angle of attack

压力系数为-10-5dB/Pa。传声器的前置放大器与Mueller-BBM数据采集系统相连，该系统最多支持32路传声器同步采集，数据采样率最高达102.4 kHz。图4所示为BSWA传声器及32路通道的BBM数据采集系统。

图4 BSWA传声器及BBM数据采集系统 Fig.4 BSWA microphone and BBM data acquirement system

为了保证测量精度，在测量开始前，采用标准声源(1 000 Hz，140 dB)对传声器进行了校准。本实验采样频率为32 768 Hz，采样时间为10.75 s，每个状态进行了两组测量，后处理取其代数平均。数据处理时取8 192个数据点进行快速傅里叶变换(FFT),采用Welch法求取声压功率谱密度，数据重叠50%，平均170次，频率分辨率为4 Hz。

2 实验结果

2.1 不稳定噪声频谱特征

图5所示为基准叶片边界层不稳定噪声典型声压级(SPL)频谱，图中，fmax表示幅值最大的离散单音频率，f表示幅值较小的单音频率。不稳定噪声频谱形状可以分为两类：第一类为“钟形”结构，包含多重离散单音噪声，如图5(a)所示；第二类为频带较窄的单音噪声，如图5(c)所示。背景噪声频谱中568 Hz处存在一个单音，当风洞出口速度为0 m/s时此单音依然存在，推测为经风洞传入消声室内的噪声，由于其频率较低且幅值较小，影响可以忽略。

图6所示为基准叶片总声压级(OASPL)随来流速度的变化关系，总声压级求取范围为 100～16 384 Hz。实验共测量了4个速度，20、40、60、80 m/s。以20 m/s状态OASPL为参考值，分别用20、40、60、80m/s状态下的OASPL减20 m/s状态下的OASPL得到总声压级之差ΔOASPL。图中包括0° 攻角和5° 攻角结果，0° 攻角状态下声功率近似与来流速度的6次方成正比。

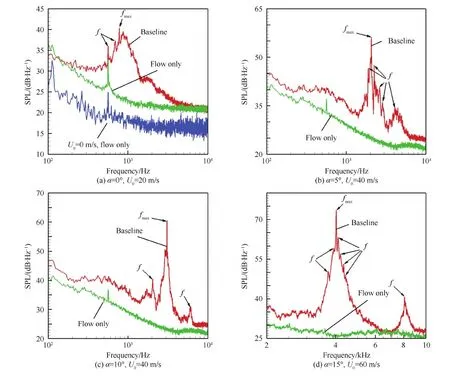
图5 基准叶片不稳定噪声频谱分析Fig.5 Spectrum analysis of baseline blade instability noise

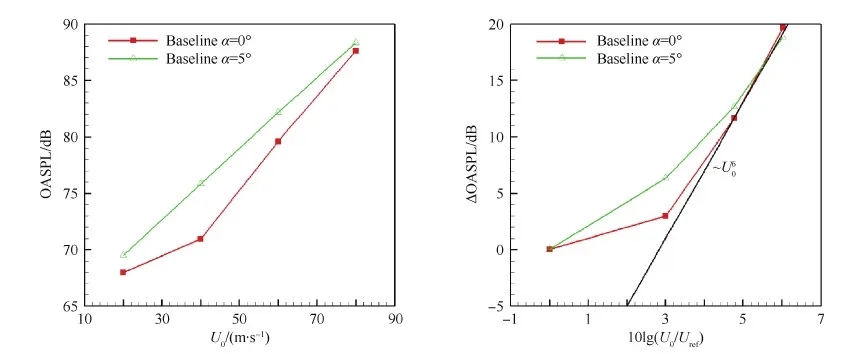
图6 基准叶片总声压级与来流速度的关系Fig.6 Relationship between OASPL and inflow velocity of baseline blade

2.2 尾缘锯齿对不稳定噪声的影响

2.2.1 0° 攻角状态

图7所示为0°攻角4个不同速度下仿生学尾缘锯齿结构对叶片尾缘自噪声辐射特性的影响。由图7(a)可知，在来流速度为20 m/s时，基于叶片弦长的雷诺数为2×105，基准叶片与3种尾缘锯齿结构均产生了“干草垛”形的噪声频谱，其中包括多重离散单音噪声，3种尾缘锯齿结构均增大了不稳定噪声，小振幅锯齿H5λ4增大的最多，达10 dB以上。H10λ4尾缘锯齿叶片在10 000 Hz附近产生了额外的单音噪声，进一步分析可知，此单音频率不随速度变化而变化。随着来流速度的增加，雷诺数增大，基准叶片不稳定噪声消失，但尾缘锯齿叶片不稳定噪声始终存在，且锯齿振幅越大，不稳定噪声越向低频移动，噪声幅值也越大。在高速状态下，尾缘锯齿“诱导”产生了不稳定噪声。

图9所示为基准叶片及3种尾缘锯齿叶片总声压级随来流速度的变化关系，0° 攻角状态下尾缘锯齿均增大了4个速度下的噪声，但尾缘锯齿的引入并未改变总声压级随来流速度的变化关系，锯齿叶片声功率仍近似与来流速度的6次方成正比。图中同时给出了未安装叶片时的背景噪声，由于有机玻璃板的存在，背景噪声并不符合喷流噪声的8次方定律。

图7 尾缘锯齿对叶片不稳定噪声的影响(α=0°)Fig.7 Effect of trailing edge serrations on blade instability noise (α=0°)

图8 总声压级指向性(α=0°)Fig.8 OASPL directivity (α=0°)

图9 锯齿叶片总声压级与来流速度的关系Fig.9 Relationship between OASPL and inflow velocity of serrated blades

2.2.2 大攻角状态

图10所示为5° 攻角状态下尾缘锯齿结构对叶片不稳定噪声的影响。可以看出，在两个速度下，基准叶片与尾缘锯齿叶片均产生了边界层不稳定噪声。尾缘锯齿振幅越大，不稳定噪声越向着低频移动。H10λ4尾缘锯齿叶片降噪效果最为明显，可见尾缘锯齿振幅对不稳定噪声有较大影响，锯齿振幅并非越大越好。

图11所示为5°攻角下总声压级指向性结果， 当来流速度为40 m/s时，H10λ4锯齿翼型在各个方位角均取得了明显的降噪效果。

图12所示为10°攻角状态下尾缘锯齿结构对叶片尾缘自噪声的影响，在大攻角状态下，基准叶片边界层不稳定噪声频谱逐渐由“钟形”结构转变为频带较窄的单音噪声，在高频范围出现了新的不稳定噪声，3种尾缘锯齿均减弱甚至抑制了不稳定噪声。在两个速度下，H10λ4尾缘锯齿叶片降噪效果最好，降噪量最高可达30 dB。由此可知，在锯齿波长一定的情况下，尾缘锯齿振幅并非越大越好，在一定的流动状态下，锯齿振幅存在一个最佳值。

图13所示为10°攻角下总声压级指向性结果，由于尾缘锯齿减弱甚至完全抑制了不稳定噪声，降噪效果非常明显，各个方位角均取得了5～10 dB的降噪效果。

图14所示为15°攻角状态下尾缘锯齿结构对叶片尾缘自噪声的影响，在来流速度为40 m/s时，基准叶片与3种尾缘锯齿叶片不稳定噪声均消失，尾缘锯齿结构会增大叶片低频段(800～2 000 Hz)尾缘自噪声，且尾缘锯齿振幅越大，噪声增加的越多，最大可达6 dB。当来流速度增大到60 m/s时，基准叶片再次出现不稳定噪声，而3种锯齿叶片均抑制了不稳定噪声，降噪量高达40 dB。但同时尾缘锯齿会增大低频段(1 000～2 500 Hz)噪声，最大达6 dB。可见不稳定噪声对攻角以及雷诺数都是比较敏感的。

对照组给予经皮腰椎间盘摘除术联合臭氧消融治疗,研究组患者给予射频热凝术联合臭氧消融治疗。射频热凝术:患者取俯卧位,保持患者腰椎过曲位,常规消毒、铺巾,确定穿刺点,进针到靶点,设定频率,检出患者最大耐受温度,采用最大耐受温度连续治疗180s,在治疗过程中,注意患者的耐受性,及时调整射频针的位置。臭氧消融:在射频热凝术治疗之后,拔除电极针,接上已经灌入10ml的臭氧的灭菌注射器,缓慢注射8ml。并观察患者气态弥散情况,观察半小时,结束治疗。

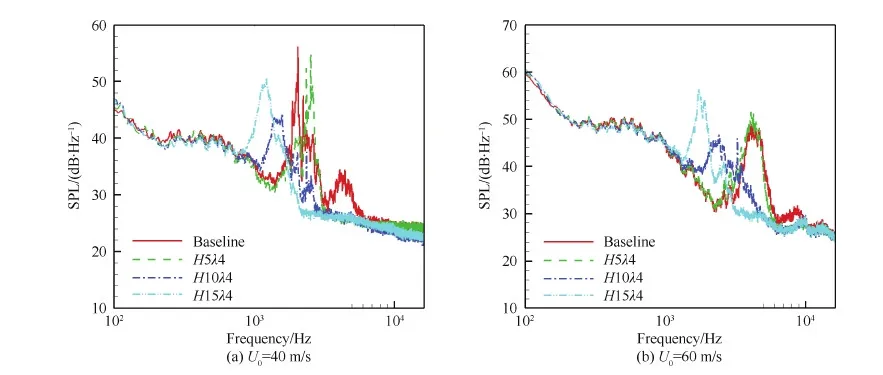
图10 尾缘锯齿对叶片不稳定噪声的影响(α=5°)Fig.10 Effect of trailing edge serrations on blade instability noise (α=5°)

图11 总声压级指向性(α=5°)Fig.11 OASPL directivity (α=5°)

图12 尾缘锯齿对叶片不稳定噪声的影响(α=10°)Fig.12 Effect of trailing edge serrations on blade instability noise (α=10°)

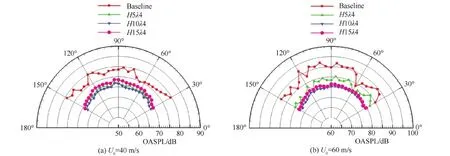
图13 总声压级指向性(α=10°)Fig.13 OASPL directivity (α=10°)

图14 尾缘锯齿对叶片不稳定噪声的影响(α=15°)Fig.14 Effect of trailing edge serrations on blade instability noise (α=15°)

图15所示为15°攻角下总声压级指向性结果。从图中可以看出，来流速度为40 m/s时，不稳定噪声消失，尾缘锯齿增大了叶片噪声，来流速度为60 m/s时，尾缘锯齿结构抑制了不稳定噪声，降噪效果非常明显。

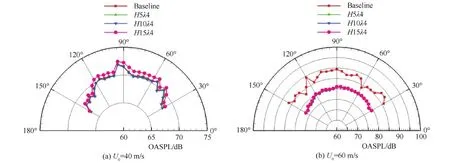
图15 总声压级指向性(α=15°)Fig.15 OASPL directivity (α=15°)

2.3 不稳定噪声峰值频率

Paterson等[3]提出“涡脱落模型”，基于平板层流边界层理论给出了不稳定单音噪声频率预测公式：

(4)

式中：υ为运动黏性系数。

Tam[4]否定了Paterson的“涡脱落模型”，首次提出了“声学反馈回路模型”，给出了如下不稳定离散单音噪声频率预测公式：

(5)

式中：n为正整数。

Brooks等[2]则通过大量实验给出了如下预测叶片边界层不稳定噪声频率的半经验公式：

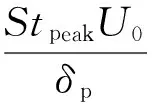
(6)

Stpeak=St×10-0.04αe

(7)

St=

(8)

(9)

(10)

图16为不同攻角不同速度状态下不稳定单音噪声频率分布，为表示清晰起见，图中并未给出图7所示的10 000 Hz左右的高频单音。图中同时给出了采用Paterson模型、Tam模型和Brooks模型预测结果。从图中可以看出，Paterson模型与Brooks模型预测结果相近，对基准翼型而言，实验结果与Brooks模型吻合得更好。尾缘锯齿会降低不稳定单音峰值频率，且锯齿振幅越大，越向低频移动，尾缘锯齿叶片不稳定噪声频率近似与来流速度的1.2次方成正比，如图16(a)所示。需要指出的是，由于本文实验测量速度数目较少，并未观察到Paterson实验所发现的“阶梯形”结构。

图16 不稳定单音噪声频率分布Fig.16 Frequency distribution of instability tonal noise

3 结 论

1) 叶片层流边界层不稳定噪声对雷诺数及攻角均较为敏感，在一定的雷诺数及攻角组合状态下才会出现不稳定噪声。

2) 0°攻角状态下，尾缘锯齿结构会增强甚至诱导产生不稳定噪声，显著增大叶片尾缘自噪声；大攻角状态下，尾缘锯齿结构可以减弱甚至完全抑制不稳定噪声，降噪量可达40 dB。当基准叶片与尾缘锯齿叶片均不存在不稳定噪声时，尾缘锯齿会增加低频段尾缘自噪声，且锯齿振幅越大噪声增加越多，最大可达6 dB。

3) 在锯齿波长一定的情况下，锯齿振幅并非越大越好，H10λ4锯齿翼型降噪效果最好，尾缘锯齿可以影响叶片尾缘附近流场，破坏不稳定噪声产生所需的声学反馈回路，进而降低不稳定噪声。

4) 尾缘锯齿可以降低不稳定噪声频率，且锯齿振幅越大，不稳定噪声越向低频移动，不稳定噪声频率近似与来流速度的1.2次方成正比，小于基准翼型的1.5次方幂次律。

[1] HOWE M S. A review of the theory of trailing edge noise： NASA CR-3021[R]. Washington， D.C.: NASA， 1978.

[2] BROOKS T F, POPE D S, MARCOLINI M A. Airfoil self-noise and prediction： NASA RP-1218[R]. Washington， D.C.: NASA， 1989.

[3] PATERSON R W, VOGT P G, FINK M R, et al. Vortex noise of isolated airfoils[J]. Journal of Aircraft, 1973, 10(5): 296-302.

[4] TAM C K W. Discrete tones of isolated airfoil[J]. Journal of the Acoustical Society of America, 1974, 55(6): 1173-1177.

[5] ARBEY H, BATAILLE J. Noise generated by airfoil profiles placed in a uniform laminar flow[J]. Journal of Fluid Mechanics, 1983, 134: 33-47.

[6] LOWSON M V, FIDDES S P, NASH E C. Laminar boundary layer aeroacoustic instabilities[C]//32nd Aerospace Sciences Meeting & Exhibit. Reston： AIAA， 1994.

[7] NASH E C, LOWSON M V, MCALPINE A. Boundary-layer instability noise on aerofoils[J]. Journal of Fluid Mechanics, 1999, 382: 27-61.

[8] KINGAN M J, PEARSE J R. Laminar boundary layer instability noise produced by an aerofoil[J]. Journal of Sound and Vibration, 2009, 322: 808-828.

[9] PLOGMANN B, HERRIG A, WURZ W. Experimental investigations of a trailing edge noise feedback mechanism on a NACA 0012 airfoil[J]. Experiments in Fluids, 2013, 54: 1480.

[10] GOLUBEV V V, NGUYEN L, MANKBADI R R, et al. On flow-acoustic resonant interactions in transitional airfoils[J]. International Journal of Aeroacoustics, 2014, 13(1): 1-38.

[11] DESQUESNES G, TERRACOL M, SAGAUT P. Numerical investigation of the tone noise mechanism over laminar airfoils[J]. Journal of Fluid Mechanics, 2007, 591: 155-182.

[12] ARCONDOULIS E J G, DOOLAN C J, ZANDER A C, et al. A review of trailing edge noise generated by airfoils at low to moderate Reynolds number[J]. Acoustics Australia, 2010, 38(3): 129-133.

[13] INASAWA A, NINOMIYA C, ASAI M. Suppression of tonal trailing-edge noise from an airfoil using a plasma actuator[J]. AIAA Journal, 2013, 51(7): 1695-1702.

[14] HOWE M S. Noise produced by a sawtooth trailing edge[J]. Journal of the Acoustical Society of America, 1991, 90(1): 482-487.

[15] HOWE M S. Aerodynamic noise of a serrated trailing edge[J]. Journal of Fluids and Structures, 1991, 5: 33-45.

[16] FINEZ A, JONDEAU E, ROGER M, et al. Broadband noise reduction of a linear cascade with trailing edge serrations[C]//7th AIAA/CEAS Aeroacoustics Conference. Reston: AIAA, 2011.

[17] GRUBER M, JOSEPH P F, CHONG T P. Experimental investigation of airfoil self-noise and turbulent wake reduction by the use of traling edge serrations[C]//16th AIAA/CEAS Aeroacoustics Conference. Reston: AIAA, 2010.

[18] MOREAU D, DOOLAN C J. Noise-reduction mechanism of a flat-plate serrated trailing edge[J]. AIAA Journal, 2013, 51(10): 2513-2522.

[19] BROOKS T F, MARCOLINI M A, POPE D S. Airfoil trailing-edge flow measurements[J]. AIAA Journal, 1986, 24(8): 1245-1251.

陈伟杰男， 博士研究生。主要研究方向： 叶轮机械气动声学。

Tel.: 13468775824

E-mail: cwj@mail.nwpu.edu.cn

乔渭阳男， 博士， 教授， 博士生导师。主要研究方向： 叶轮机气体动力学， 航空发动机气动声学。

Tel.: 029-88482195

E-mail: qiaowy@nwpu.edu.cn

*Correspondingauthor.Tel.：029-88482195E-mail:qiaowy@nwpu.edu.cn

Bladeboundarylayerinstabilitynoisewithtrailingedgeserrations

CHENWeijie,QIAOWeiyang*,TONGFan,DUANWenhua,LIUTuanjie

SchoolofPowerandEnergy,NorthwesternPolytechnicalUniversity,Xi’an710129,China

Theeffectofthreetrailingedgeserrationsofthesamewavelength(4%ofthechordlength)anddifferentamplitudes(5%,10%and15%ofthechordlength)onbladelaminarboundarylayerinstabilitynoiseisinvestigatedexperimentallyatlowtomoderateReynoldsnumber(2×105-8×105)anddifferentangleofattacks.Itcanbeconcludedthatatzeroangleofattack,trailingedgeserrationscanreinforceoreveninduceboundarylayerinstabilitynoisetoleadtoanincreaseofthebladeself-noise.Atlargerangleofattack,instabilitynoiseisreducedoreventotallysuppressedbythetrailingedgeserrations,resultinginamaximumnoisereductionof40dB.Thenoisereductionmechanismcanbeattributedtothedestructionoftheacousticfeed-backloop,whichisessentialforthegenerationofinstabilitynoise,bythetrailingedgeserrations.Trailingedgeserrationswilldecreasetheinstabilitytonalnoisefrequency,andtheinstabilitynoisefrequencyislowerwithlargerserrationamplitude.

trailingedgeserrations;laminarboundarylayer;instabilitynoise;acousticfeed-backloop;T-Swave

2015-12-31；Revised2016-07-06；Accepted2016-08-10；Publishedonline2016-08-121059

URL：www.cnki.net/kcms/detail/11.1929.V.20160812.1059.002.html

s：NationalNaturalScienceFoundationofChina(51276149,51476134);StateKeyLaboratoryofAerodynamicsResearchFund(SKLA20140201)

2015-12-31；退修日期2016-07-06；录用日期2016-08-10； < class="emphasis_bold">网络出版时间

时间：2016-08-121059

www.cnki.net/kcms/detail/11.1929.V.20160812.1059.002.html

国家自然科学基金 (51276149,51476134)； 空气动力学国家重点实验室研究基金 (SKLA20140201)

*

.Tel.：029-88482195E-mailqiaowy@nwpu.edu.cn

陈伟杰， 乔渭阳， 仝帆， 等． 尾缘锯齿结构对叶片边界层不稳定噪声影响的实验研究J． 航空学报,2016,37(11):3317-3327.CHENWJ,QIAOWY,TONGF,etal.AnexperimentinvestigationofbladeboundarylayerinstabilitynoisewithtrailingedgeserrationsJ.ActaAeronauticaetAstronauticaSinica,2016,37(11):3317-3327.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0232

V231

A

1000-6893(2016)11-3317-11