多自主翼伞系统建模及其集结控制
2016-11-20陈奇赵敏赵志豪马敏毓黄荣发
陈奇, 赵敏, 赵志豪, 马敏毓, 黄荣发
1. 南京航空航天大学 自动化学院, 南京 210016 2. 淮阴工学院 电子信息工程学院, 淮安 223003 3. 中航工业宏光空降装备有限公司, 南京 210022
多自主翼伞系统建模及其集结控制
陈奇1,2, 赵敏1, *, 赵志豪1, 马敏毓1, 黄荣发3
1. 南京航空航天大学 自动化学院, 南京 210016 2. 淮阴工学院 电子信息工程学院, 淮安 223003 3. 中航工业宏光空降装备有限公司, 南京 210022
当前对翼伞系统的研究主要集中在单个翼伞,但实际空投中一般需要使用多个翼伞,才能完成大量物资、装备的空投补给任务,而多个翼伞同时空投时,将会出现翼伞需要集结、相互间需要避免碰撞等在单翼伞空投时不存在的问题。现有的单翼伞系统已能通过GPS/惯导系统及其他板载传感器实现自主飞行,针对多个自主翼伞的空投任务设计算法,以控制下降翼伞之间的相互运动,实现多翼伞系统的集结和避碰。首先以质点模型为起点,通过引入新的独立变量,并将翼伞运动转换至风固定坐标系,使得单个翼伞质点模型降维为非线性降阶模型,进而得到多自主翼伞模型,在此基础上提出了一种集结控制算法,利用每个翼伞自身的状态信息和相邻翼伞的状态信息,采用势场法使得多翼伞实现集结并避免碰撞,最后一致地降落至地面。仿真结果表明多个自主翼伞实现了集结,减小了翼伞的着陆散布,降低了翼伞之间的碰撞风险,验证了该方法的有效性,可以为进一步研究多自主翼伞协同控制提供理论参考。
单翼伞; 质点模型; 降阶模型; 多翼伞; 集结控制; 避碰
自主翼伞可以根据传感器获得的信息做出操控动作,将物资快速运输到普通运输工具不易到达的地区,将传统的地面保障提升为三维的垂直保障,因此无论是在军用、民用,还是在人道主义救援方面,都有巨大的需求,其中“自主”一词指的是每个对象能利用自身传感器所获得的信息,根据内部规则以及其所处的复杂环境中而各自作出反应的能力[1]。过去50年来,国内外研究者付出了大量努力,设计了一系列不同载荷重量的翼伞,发展了多种单翼伞导航、制导和控制(Guidance, Navigation, and Control,GNC)算法[2-3],使单翼伞可利用全球定位系统(Global Positioning System,GPS)、惯性导航系统 (Inertial Navigation System,INS)和其他板载传感器,实时跟踪参考轨迹,自主飞行到目标点。
目前已有多个翼伞空投项目在航空、军用等领域成功进行了试验。比如美国的X-38项目,该项目成功地利用翼伞将重达11 t的成员返回舱原型机制导飞回地球,其着陆精度达360 m[4]。另一个翼伞项目是欧洲航天局的FASTWing CL,该项目开发的高性能翼伞面积达300 m2、滑翔比超过5、载荷重量达到6 t[5]。美欧两家开发的翼伞空投系统的特点是翼伞尺寸大、载荷能力强,但单个翼伞系统价格较为昂贵,系统一旦发生故障,将无法完成空投任务,造成重大损失。
翼伞的另一个发展思路是用多个中小型翼伞代替单个大型翼伞,以完成单个大型翼伞的功能,为此美国国防部(Department of Defense,DoD)主导开发了联合精确空投系统(Joint Precision Airdrop System,JPADS)[6],JPADS主要应用于军事行动,能够在防区外、近万英尺的高度将人员和物资准确地投送至目的地。该系统有多个型号,包括Screamer尖叫者翼伞系统、DragonFly蜻蜓翼伞系统,以及载荷更低的Mosquito蚊子翼伞系统、PROVIDER翼伞系统,其中PROVIDER翼伞系统可用于战场监视、侦查,多个PROVIDER翼伞系统之间可以通过相互的空中射频信息实现通信,然后通过中继PROVIDER翼伞与SATCOM跟踪卫星实现通信。
从国外的情况来看,以多个中小型翼伞一起投放代替单个大型翼伞已渐成主流。在抗震救灾时,单个大型翼伞显然不敷使用,需要大量制导翼伞才能完成紧急救援物资的精确空投。在军事部署时,多个翼伞需根据当前战术状况,以一定的战斗队形编队投放,使作战力量在着陆后不用重组,无延时的投入战斗,以此增加作战力量的生存能力和作战有效性,同时多个翼伞还可以将载荷空投到多个指定区域。另外,在一些空投任务中,需要运送笨重的分段工程设备,希望多自主翼伞以一定的编队(彼此之间保持一定的相对位置)空投到着陆点,以便着陆后按一定相互位置将设备组装到一起。
目前在进行多翼伞投放时,翼伞之间还是各自为政,相互间没有协调沟通,这使得翼伞一方面存在碰撞可能,另一方面着地散布面较大。因此在将大量物资空投到目标点时,若能实现多个高滑翔比自主翼伞的集结控制,对翼伞空投系统的发展有重要意义。国外学者近年来已开始了这方面的探索,Kaminer等提出了多翼伞协同空投问题解决方案,以确保在严格空间约束情况下翼伞无碰撞下降,其解决方案依赖于问题模型的时间和空间解耦[7]。Calise和Preston通过模拟生物系统的蜂拥/群集行为,试图改进翼伞系统制导和控制系统设计,通过仿真验证了概念可行性,并进行了5个翼伞的协同控制飞行测试[8]。Gurfil等提出了一个自顶向下的设计方法来管理多翼伞空投任务,开发了制导算法和任务管理方法来处理翼伞组的故障和异常事件[9]。Rosich和Gurfil提出了一种新的航迹生成方法,并发展了一种基于行为的规则,以控制多个下滑翼伞之间的相对运动,提出的简单规则使得多翼伞出现群集行为[10]。目前中国对单个翼伞的研究已经比较深入,熊菁等分析了回收物和伞体之间的相对运动情况,建立了翼伞系统非刚性连接模型[11];朱旭和曹义华利用数值模拟方式,研究了不同几何参数对翼伞气动性能的影响[12];北京空间机电研究所的李春等研制了具有自动归航和人工遥控归航2种工作模式的精确定点归航翼伞控制系统,地面联试和负载试验表明设计的控制系统满足了可控翼伞定点归航的需要[13];高海涛等提出了基于Gauss伪谱法的归航轨迹容错设计方法,表明在约束情况下,翼伞系统无论在正常和单电机异常工作时都可以顺利到达目标点,获得高精度的飞行轨迹[14];梁海燕等采用控制变量参数化与时间尺度变换相结合的优化算法对翼伞系统的最优控制问题进行求解,有效地提高了翼伞系统的精度[15];陈建平等应用拉格朗日方程建立翼伞系统的纵向飞行力学模型,深入分析了系统参数以及开伞状态对翼伞系统纵向飞行性能的影响规律[16]。总的说来,中国学者对单个翼伞的研究,不管是理论还是实践方面都取得了丰硕的成果,但目前还没有学者对多自主翼伞的建模和集结控制问题进行研究。
综上所述,多自主翼伞的控制在国外已成为翼伞制导导航控制研究领域的一个新热点。如何建立较为简单实用的单翼伞模型,并将其扩展至多翼伞系统,进一步地,控制多个下降翼伞之间的相对运动,避免彼此碰撞,协调一致的降落,已成为亟需解决的问题。本文针对上述问题,探索多自主翼伞的建模和集结控制,发展避免翼伞碰撞的集结控制算法,为翼伞技术的进一步发展提供理论参考。
1 翼伞建模
翼伞由柔性纺织材料制成,充气后形状类似于飞机的机翼。大多数情况下,翼伞主要飞行模式为滑翔、转弯、减速以及雀降等。翼伞通过下拉连接在伞衣后缘两侧的控制线实现控制,使伞衣后缘出现所谓的后缘偏转。右侧和左侧后缘偏转分别定义为δr和δl,两者的平均值称为对称后缘偏转,其值为δs=(δl+δr)/2,δs增加时会导致升力和阻力同步增加,升阻比基本保持不变,但会降低翼伞速度,因此一般通过对称偏转后缘的方式控制下滑速度的大小。非对称后缘偏转偏差量定义为δa=δl-δr,该偏差量产生非对称阻力,使翼伞发生倾斜,产生作用在载荷上的离心力,使翼伞向更低一侧的后缘方向转弯。翼伞系统结构如图1所示。

图1 翼伞系统结构Fig. 1 Structure of parafoil system
翼伞集结控制问题的求解需要较为简单的、易于处理的系统模型,以描述翼伞运动特性。如果不需要了解翼伞系统各部分之间的相对运动情况,而仅需掌握翼伞系统质心的运动轨迹,采用质点模型通常就足以描述翼伞系统的运动特性。因此本节首先分析翼伞质点模型,进而通过转换得到等价的非线性降阶模型。
1.1 翼伞运动方程
考虑图2所示的翼伞转弯飞行后视图,其中:L为升力与侧力的合力,W为重力,φ为伞体倾斜角,σ为合力L的倾斜角。

图2 翼伞系统转弯飞行受力分析后视图 Fig. 2 Back view diagram of parafoil system turning flight force analysis
图3为翼伞受力分析侧视图,其中:V为翼伞速度矢量大小,D为与速度矢量反向的气动阻力大小,γ为翼伞飞行航迹角,其值为负。


图3 翼伞系统转弯飞行受力分析侧视图 Fig. 3 Side view diagram of parafoil system turning flight force analysis

图4 翼伞系统转弯飞行俯视图Fig. 4 Top view diagram of parafoil system turning flight
翼伞空投一般在近地空间完成,因此可假定地球是平的、非旋转的。考虑风速在x轴和y轴方向的水平分量wx和wy为常值,根据受力分析,可得翼伞质点运动方程[17]为
(1)
(2)

(3)
此时式(2)和式(3)即构成翼伞质点模型[10,17]。
在稳态平衡情况下由式(1)可知
D=-Wsinγ
(4)
Lcosσ=Wcosγ
(5)
将式(4)与式(5)两式相除,可得翼伞的飞行航迹角为
(6)
可见γ由升阻比L/D和倾斜角σ确定。为递推求解运动方程式(2)和式(3),还需确定V、L/D以及σ等参数。对给定索具角以及对称后缘偏转的翼伞,这几个参数可以表示为后缘差分偏转值和高度的函数:
(7)
式中:L/D(δa)为不同后缘差分偏转值的函数。如果记σ0(δa)为某给定高度下的稳态广义倾斜角,则其他高度的σ可以近似表示为

(8)
式中:ρ(h)为空气密度,是高度的函数;h0为参考高度。
下滑角γ由式(6)给出,是倾斜角σ的函数。令γ0为对称滑翔状态下(即σ=0,δa=0)的飞行航迹角:
(9)

(10)
当σ≠0时,有
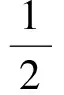
(11)
根据文献[10]中假设CL0≈CL,利用式(10)和式(11)可得

(12)
式中:V0为直线下滑时的空速。一般用等效稳态下滑空速Veq0表示下滑空速较为方便,Veq0可在零差分后缘偏转下测量得到,即

(13)
到此所有翼伞飞行参数都已根据控制输入(后缘偏转)、翼伞的状态(高度)以及翼伞常值参数进行了定义。对给定翼伞,上述翼伞常参数依赖于索具角、对称后缘偏转以及翼载荷,至于空气密度ρ(h)可以从大气模型得到。
对一般翼伞模型来说,最佳滑翔比可以在50%对称后缘偏转情况下获得。该对称后缘偏转记为后缘偏转基准值。控制算法将在这个值附近产生差分后缘偏转指令:降低翼伞一侧后缘的同时,以相同大小提升另外一侧后缘。这种控制模式下两侧后缘都不会饱和;此外,在后缘偏转值较小时有助于避免翼伞后缘反翘。一般情况下还可以假设σ≈φ[10],因为从仿真或空投测试中辨识φ比σ更容易。在上述操纵模式下,L/D和σ0可认为线性依赖于δa。文献[9]给出了某型翼伞的特性参数,如表1所示。
基于表1中的参数,本文在MATLAB/SIMULINK环境下建立了翼伞系统质点模型并进行了仿真实验。在δa=0时,翼伞首先直线滑翔飞行,在δa=0.5时,翼伞右转弯飞行,如图5所示。

表1 翼伞特性参数Table 1 Parafoil characteristic parameters

图5 翼伞飞行航迹图Fig. 5 Parafoil flight path diagram
1.2 翼伞降阶模型
上述翼伞模型较为完整地反映了翼伞的动力学特性,但在利用该模型对多翼伞进行建模和分析时较为不便,因此有必要进行进一步的简化。
1.2.1 独立变量引入
定义
τ(t)=h(t0)-h(t)
(14)
式中:h(t0)为翼伞初始投放高度;τ为翼伞已下降的高度,不失一般性,假定目标点海拔高度为0,即h(tf)=0,tf为翼伞降落到目标点的时间,则τ(t0)=0,τ(tf)=h(t0)。在翼伞滑翔下降过程中,一般实际高度是单调减少的,因此,已下降高度值τ是单调增加的。令τ为新的独立变量,则由式(2)可知
dτ=-Vsinγdt
(15)
为了区分对时间的导数和对下降高度τ的导数,定义后者为(·)′。则翼伞系统方程降阶为
(16)
引入新的独立变量有两个好处,首先,它将翼伞质点模型由4阶降低至3阶,从而减少了航迹计算的开销;其次,在给定初始高度下,对任何一条规划航迹,最终下降高度τf总是固定的。此外在不引起歧义的情况下,为表述方便,将τ重新视为时间。
1.2.2 风固定坐标系
为进一步简化运动方程,还可以通过消除风偏移的影响,定义新的坐标系以进一步简化系统模型。对式(16)做移项处理,并令

(17)
对式(17)从τ到τf积分,且令τ=τf时风固定坐标系与惯性坐标系重合,则在风固定坐标系下,翼伞位置为
(18)
从式(18)可知,风固定坐标系是随气团运动的坐标系,坐标轴方向与惯性坐标系坐标轴方向一致,其x轴方向指向正北,原点随气团一起运动。
利用式(16)和式(18),可得风固定坐标系下单个翼伞降阶模型为
(19)
在不引起歧义的情况下,将式(19)翼伞降阶模型重写为
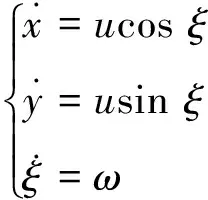
(20)

u和ω可视为系统的等效控制输入,分别表示等效线速度输入和等效角速度输入,该模型需要根据翼伞系统运动特性加以约束,根据文献[10]的计算,翼伞线速度范围为18.8~32 m/s,角速度范围为[-0.178, 0.178] rad/s。实际上,可以通过对称下拉两侧伞绳以控制线速度,通过差分下拉两侧伞绳以控制转弯角速度。
此外,从式(20)可知,翼伞系统本质上是非线性的。在式(20)所描述的单个翼伞的基础上,可考虑多个翼伞一起空投的情况,但与单翼伞时不一样的是,此时更多的需要考虑翼伞之间的一致性和避免碰撞问题,故可以将每个翼伞视为一个智能体。智能体一般定义为可以通过自身传感器感知自身状态并同环境交互的实体,目前翼伞已经可以通过伞载传感器感知自身和环境的状态,并做出相应的控制操作。
2 多翼伞结集控制
2.1 图论和网络拓扑[18-19]
信息交换是集结控制的基础,通常用图来表示一组智能体信息交换的拓扑网络。下面简要介绍图论基础。

关于多翼伞底层网络拓扑,假设以动态方程式(20)构成的多自主翼伞系统形成了平衡和静态通信网络,且一直保持强连接。这意味着所有翼伞在投放时就已建立了通信连接,且一直保持连接直到着陆,本文暂不考虑时变网络拓扑。
2.2 一致性

(21)

2.3 势场力
本文采用人工势场法实现多翼伞系统集结控制。人工势场是势函数的梯度,本文定义的势场力为

(22)
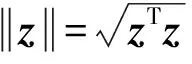
2.4 翼伞集结控制器设计
本节针对以式(20)为基础构成的多翼伞系统,基于一致性设计控制律,使多个翼伞集结到某点,并通过仿真验证算法的有效性。考虑大气坐标系下n个不同初始位置和初始航向的翼伞智能体。相邻翼伞之间可以交换包括位置在内的信息。所有智能体将在某个共同点实现一致性,该点为初始位置的平均点,翼伞在该点集结。实现集结后还需要保证翼伞相互之间不发生碰撞,则不仅需要考虑智能体之间的吸引力,在翼伞集结到某个设定的安全距离后,还要进一步考虑相互之间的排斥力。在安全距离附近,相互之间吸引力和排斥力相等,当小于安全距离时,排斥力大于吸引力,故翼伞不再进一步集中,可避免相互之间的碰撞事故。因此考虑智能体间的势函数为
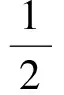
(23)
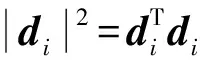
(24)

(25)

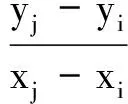
(26)

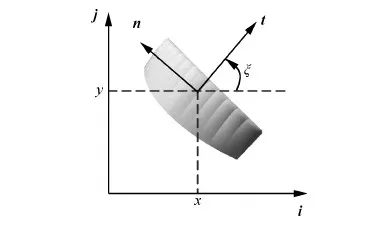
图6 风固定坐标系下翼伞方位矢量图Fig. 6 Parafoil azimuth vector diagram in atmospheric coordinates frame
当智能体将各自方向调整到相邻智能体方向角均值的时候,所有智能体将向彼此靠近;当智能体集结时,智能体相互之间的相对速度将趋向于0。
本文在MATLAB/SIMULINK环境下建立了多自主翼伞模型,在本文设计的集结控制算法作用下,得到如图7所示翼伞集结结果,4个翼伞智能体在风固定坐标系下实现集结,并收敛到某点,同时所有翼伞的航向角实现一致。本文设定的空投高度为1 200 m,初始条件为
x0=[-1 000 1 200 1 000 -100]T
y0=[1 200 -1 200 800 -1 500]T
ξ0=[π/4 -π/2 2π/3 π]T
由图7可见,在集结控制算法作用下,4个初始位置和初始速度方向都不同的翼伞逐渐向彼此靠拢,最终集结到一起,然后一致地向地面滑翔,且在集结后翼伞相互之间没有发生碰撞。因为碰撞只有在时间和空间同时重合才会发生,但通过检视翼伞的运动数据,翼伞在同一时刻其空间位置并无重合,相互之间保持了一定的排斥距离。图8为翼伞降落的三维轨迹图,需要说明的是,翼伞在集结后,虽然已集中到一起,但相互之间是保持了一定间距的。图9和图10分别为翼伞等效线速度输入和等效角速度输入,此时翼伞的对称下拉量和差分下拉量不会超出翼伞动态特性范围。

图7 翼伞实现集结并保持安全间距的二维轨迹图 Fig. 7 2D trajectories for parafoils rendezvous and maintaining a safe distance

图8 翼伞实现集结并保持安全间距的三维轨迹图 Fig. 8 3D trajectories for parafoils rendezvous and maintaining a safe distance
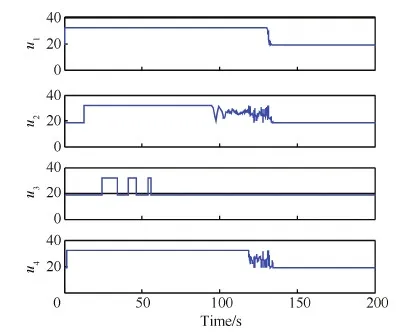
图9 翼伞等效线速度输入控制量uFig. 9 Parafoil equivalent linear velocity control inputs u
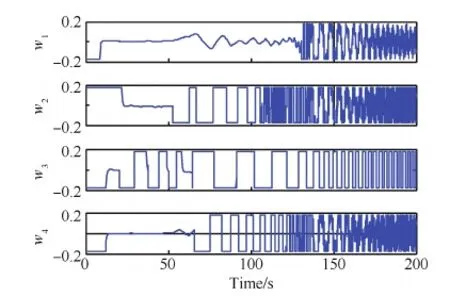
图10 翼伞等效角速度输入控制量wFig. 10 Parafoil equivalent angular velocity control inputs w
2.5 稳定性分析
本节将分析为什么会出现集结行为。由式(20)描述的n个翼伞多智能体在集结控制器式(25)作用下,闭环系统动态方程为
(27)
式中:
Hi=
另外,由于本文考虑拓扑图为平衡图,所以式(27)中dj=-di。
考虑定义在紧集内关于式(27)的连续可微函数:
Vi关于时间t的导数为
因为Hi为对称正半定阵,因此在集合上有


3 结 论
从翼伞质点模型出发,推导了翼伞降阶非线性等效模型,并将其扩展至多翼伞情况。考虑到翼伞的动态特性,根据翼伞的实际飞行速率和转弯速率范围对等效模型进行了限制,得到的模型更符合翼伞特性。本文基于人工势场法设计的集结控制器有如下特点:
1) 在开始阶段,当翼伞散布比较大时,相互间吸引势函数较大,彼此进一步靠拢;彼此间间距缩小后,排斥势函数逐渐增大,当间距靠近安全距离后,不再进一步缩小,保证了翼伞的安全。从不同位置空投的多翼伞系统可以集结到一起,降低了翼伞的着陆散布;且彼此不会发生碰撞,减小了空投任务的风险。因此,势场法可以用于处理多翼伞的集结控制问题。
2) 每个自主翼伞之间彼此高度连接,但所有成员并没有连到一个中央枢纽上,而是靠成员间的互相通信实现分布式控制。由于没有总的控制中心,设计的控制器是去中心、分布式的,每个翼伞都具有自主的特质。
3) 多自主翼伞的使用比单个大型翼伞有更多的优点,多个翼伞相互协作,可以更灵活的完成复杂空投任务;使用多个中低成本的翼伞可以产生冗余,从而比采用一个功能强大而昂贵的翼伞更加能容忍错误,多个廉价中小型翼伞同时投放,可以替代单个大型翼伞的功能。
需要指出的是,多自主翼伞系统的性能很大程度上依赖于翼伞之间的交互,本文得到的结果是在翼伞为强连通拓扑下获得,具有一定的保守性,需要进一步改进。此外,还需要进一步通过风洞试验或者流体动力学数值仿真等方式,得到等效控制输入和实际的伞绳下拉量之间的显性表达式。未来还要做的工作,是基于已经得到的多翼伞模型,考虑多翼伞的集结、编队以及目标点跟踪、以及对山峰、火炮阵地的避障等,设计出整体的控制框架,以进一步推动多翼伞的协同降落研究。
[1] 凯文· 凯利. 失控——全人类的最终命运和结局[M]. 北京: 新星出版社, 2010: 32-36.
KEVIN K. Out of control: The new biology of machines, social systems and the economic world [M]. Beijing: New Star Press, 2010: 32-36 (in Chinese).
[2] 高海涛. 翼伞系统自主归航航迹规划与控制研究[D]. 天津: 南开大学, 2014: 97-104.
GAO H T. Research on control and autonomous homing trajectory planning of parafoil system[D].Tianjin: Nankai University, 2014: 97-104 (in Chinese).
[3] SEONG-JIN L, CONNER J P, Jr, ARENA A S, Jr. An autonomous recovery system for high altitude payloads by using a parafoil[C]//AIAA Atmospheric Flight Mechanics Conference. Reston: AIAA, 2014: 2555-2563.
[4] STRAHAN A L. Testing of parafoil autonomous GN&C for X-38[C]//17th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar. Reston: AIAA, 2003: 2115-2129.
[5] WEGEREEF J W, BENOLOL S, UHL E, et al. A high-glide ram-air parachute for 6000 kg payloads, tested with the FASTWing CL test-vehicle[C]//20th AIAA Aerodynamic Decelerator Systems Technology Conference. Reston: AIAA, 2009: 2933-2941.
[6] BENNEY R, HENRY M, LAFOND K, et al. DoD new JPADS programs & NATO activities[C]//20th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar. Reston: AIAA, 2009: 2952-2969.
[7] KAMINER I I, YAKIMENKO O, PASCOAL A M. Coordinated payload delivery using high glide parafoil systems[C]//18th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar. Reston: AIAA, 2005: 1622-1629.
[8] CALISE A J, PRESTON D. Swarming/flocking and collision avoidance for mass airdrop of autonomous guided parafoils[J]. Journal of Guidance Control and Dynamics, 2008, 31(4): 1123-1132.
[9] GURFIL P, FELDMAN S, FELDMAN M. Coordination and communication of cooperative parafoils for humanitarian aid[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(4): 1747-1761.
[10] ROSICH A, GURFIL P. Coupling in-flight trajectory planning and flocking for multiple autonomous parafoils[J]. Proceedings of the Institution of Mechanical Engineers Part G—Journal of Aerospace Engineering, 2012, 226(G6): 691-720.
[11] 熊菁, 秦子增, 程文科. 翼伞系统弹性连接模型的相对运动分析[J]. 弹道学报, 2006, 18(1): 25-29.
XIONG J, QIN Z Z, CHENG W K. Analysis of relative motion of parafoil system in flexibly jointed model[J]. Journal of Ballistics, 2006, 18(1): 25-29 (in Chinese).
[12] 朱旭, 曹义华. 翼伞弧面下反角、翼型和前缘切口对翼伞气动性能的影响[J]. 航空学报, 2012, 33(7): 1189-1200.
ZHU X. CAO Y H. Effects of arc-anhedral angle, airfoil and leading edge cut on parafoil aerodynamic performance. Acta Aeronautica et Astronautica Sinica, 2012, 33(7): 1189-1200 (in Chinese).
[13] 李春, 吕智慧, 黄伟, 等. 精确定点归航翼伞控制系统的研究[J]. 中南大学学报(自然科学版), 2012, 43(4): 1331-1335.
LI C, LYU Z H, HUANG W, et al. Guidance navigation & control system for precision fix-point homing parafoil[J]. Journal of Central South University (Science and Technology), 2012, 43(4): 1331-1335 (in Chinese).
[14] 高海涛, 张利民, 孙青林, 等. 基于伪谱法的翼伞系统归航轨迹容错设计[J]. 控制理论与应用, 2013, 30(6): 702-708.
GAO H T, ZHANG L M, SUN Q L, et al. Fault-tolerance design of homing trajectory for parafoil system based on pseudo-spectral method[J]. Control Theory & Applications, 2013, 30(6): 702-708 (in Chinese).
[15] 梁海燕, 任志刚, 许超, 等. 翼伞系统最优归航轨迹设计的敏感度分析方法[J]. 控制理论与应用, 2015, 32(8): 1003-1011.
LIANG H Y, REN Z G, XU C, et al. Optimal homing trajectory design for parafoil systems using sensitivity analysis approach[J]. Control Theory & Applications, 2015, 32(8): 1003-1011 (in Chinese).
[16] 陈建平, 张红英, 童明波. 翼伞系统纵向飞行性能分析[J]. 中国空间科学技术, 2015(2): 25-32.
CHEN J P, ZHANU H Y, TONG M B, et al. Lon-gitudinal flight performance analysis of parafoil-payload systems[J]. Chinese Space Science and Technology, 2015(2): 25-32 (in Chinese).
[17] RADEMACHER B J, LU P, STRAHAN A L, et al. In-flight trajectory planning and guidance for autonomous parafoils[J]. Journal of Guidance Control and Dynamics, 2009, 32(6): 1697-1712.
[18] 许耀赆, 田玉平. 线性及非线性一致性问题综述[J]. 控制理论与应用, 2014, 31(7): 837-849.
XU Y J, TIAN Y P. A survey of linear and non-linear consensus problems in multi-agent systems[J]. Control Theory & Applications, 2014, 31(7): 837-849 (in Chinese).
[19] LISTMANN K D, MASALAWALA M V, ADAMY J. Consensus for formation control of nonholonomic mobile robots[C]//2009 IEEE International Conference on Robotics and Automation. Pisataway, NJ: IEEE Press, 2009: 3886-3891.
[20] DIMAROGONAS D V, KYRIAKOPOULOS K J. On the rendezvous problem for multiple nonholonomic agents[J]. IEEE Transactions on Automatic Control, 2007, 52(5): 916-922.
陈奇男, 博士, 讲师。主要研究方向:多翼伞建模及协同控制。
Tel: 025-84893478
E-mail: chenqi2070@126.com
赵敏男, 博士, 教授, 博士生导师。主要研究方向:翼伞空投测控系统。
Tel: 025-84893478
E-mail: xymzhao@126.com
URL:www.cnki.net/kcms/detail/11.1929.V.20160224.1700.010.html
Multipleautonomousparafoilssystemmodelingandrendezvouscontrol
CHENQi1, 2,ZHAOMin1,*,ZHAOZhihao1,MAMinyu1,HUANGRongfa3
1.CollegeofAutomationEngineering,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China2.FacultyofElectronicInformationEngineering,HuaiyinInstituteofTechnology,Huai’an223003,China3.AVICHongguangAirborneEquipmentCo.,LTD.,Nanjing210022,China
Atpresentalotofstudiesaboutparafoilsystemmainlyfocusonsingleparafoil,butitusuallyneedsmultipleparafoilstodropalargeamountofsuppliesandequipmentinactualdroptasks.Whenmultipleparafoilsaredroppedatthesametime,therewillbesomenewproblems,suchasallparafoilsneedtorendezvousandeveryparafoilshouldavoidcollisionamongeachother.TheexistingsingleparafoilcanrealizeautonomousflightbyGPS/inertialnavigationsystemandotheron-boardsensors,sointhispaperweneedtodesigncontrolalgorithmtocontroltherelativemotionofthedescendingparafoils,andtorealizetherendezvousandcollisionavoidanceofmultipleautonomousparafoils.Firstly,thispapertakestheparticlemodelasastartingpoint,transformstheparticlemodeltoareduceddimensionnon-linearmodelbyintroducingnewindependentvariables,convertstheparafoil’smovementtotheairflowfixedcoordinateframe,andthenderivesthemultipleautonomousparafoilsmodel.Moreover,thepaperproposesarendezvouscontrolalgorithmbasedonpotentialfieldmethod,useseachparafoil’sownstatusinformationandadjacentparafoil’sstatusinformation,andmakesmultipleautonomousparafoilsrendezvous,avoidcollisionsandlandtothegroundconsistently.Thesimulationresultsverifythevalidityoftheproposedmethod,andthatmultipleautonomousparafoilsimplementrendezvous,reducetheparafoils’landingspread,anddecreasethecollisionriskamongeachother.Theresultsinthispaperprovideatheoreticalreferenceformultipleautonomousparafoilscoordinatedcontrolinfurtherresearch.
singleparafoil;particlemodel;reduceddimensionmodel;multipleautonomousparafoils;rendezvouscontrol;collisionavoidance
2015-10-20;Revised2015-11-20;Accepted2016-02-19;Publishedonline2016-02-241700
s:AeronauticalScienceFoundationofChinafundedbyAviationkeyLaboratoryofScienceandTechnologyonAerospaceLife-Support(20152952038);FundingofJiangsuInnovationProgramforGraduateEducation(KYLX15_0271);TheFundamentalResearchFundsfortheCentralUniversities;AProjectFundedbythePriorityAcademicProgramDevelopmentofJiangsuHigherEducationInstitutions;Huai’anScienceandTechnologyProject(HAG2015028)
.Tel.:025-84893478E-mailxymzhao@126.com
2015-10-20;退修日期2015-11-20;录用日期2016-02-19; < class="emphasis_bold">网络出版时间
时间:2016-02-241700
www.cnki.net/kcms/detail/11.1929.V.20160224.1700.010.html
航空防护救生技术航空科技重点实验室资助的航空科学基金(20152952038);江苏省普通高校研究生科研创新计划(KYLX15_0271);中央高校基本科研业务费专项资金;江苏高校优势学科建设工程资助项目;淮安市科技计划(HAG2015028)
.Tel.:025-84893478E-mailxymzhao@126.com
陈奇, 赵敏, 赵志豪, 等. 多自主翼伞系统建模及其集结控制J. 航空学报,2016,37(10):3121-3130.CHENQ,ZHAOM,ZHAOZH,etal.MultipleautonomousparafoilssystemmodelingandrendezvouscontrolJ.ActaAeronauticaetAstronauticaSinica,2016,37(10):3121-3130.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2016.0047
V249.12
A
1000-6893(2016)10-3121-10
