直升机火控系统精度敏感性分析的BNSobol法

贺楚超， 高晓光

西北工业大学 电子信息学院， 西安 710129

直升机火控系统精度敏感性分析的BNSobol法

贺楚超， 高晓光*

西北工业大学 电子信息学院， 西安 710129

针对现有研究大都只分析了单误差源对直升机火控系统精度影响的现状，提出进行直升机火控系统精度的敏感性分析。根据传统敏感性分析法在数据量不充分或无法提供精确模型时存在的局限性，对基于贝叶斯网络和Sobol指数相结合的敏感性分析新方法(BNSobol法)进行了研究，并与传统Sobol法对比分析。结果表明BNSobol法在满足精度要求的同时还减小了对数据量的需求，它的分析不依赖于模型且可以确定出满足约束条件的具体误差源取值区间。该方法可为直升机火控系统设计研究时如何分配各模块误差大小从而提高总体效能提供参考和理论支持。

直升机； 精度评估； 敏感性分析； 火控系统； 贝叶斯网络

机枪、航炮和火箭弹等无控武器对直升机火控系统精度提出了较高的要求。在实际作战中，由于战场环境、攻击条件以及目标运动等的复杂性，导致火控系统精度受到多种因素的影响。分析这些因素对打击精度的影响及影响程度对提高火控系统性能十分重要。文献[1-3]分析了不同误差源对直升机火控系统精度的影响，并给出了减小误差提高精度的措施。由于系统正常运行时，各种误差源并非单独作用于火控系统，往往多种误差源同时存在且其间有较强的交互耦合效应，所以，当多误差源同时作用于系统时各误差源对系统总体精度的影响与各误差源单独作用时的影响会有所区别，而当系统较为复杂且误差源较多时，这个差别会更为显著。为此，本文通过寻找并分析主要误差源及误差源间的交互作用对火控系统精度的影响关系，以达到系统精度对各误差源敏感性的认知，从而实现对系统精度的有效控制。

根据文献[4]的分类方式以及作用范围，可将敏感性分析方法分为局部敏感性分析法和全局敏感性分析法。局部敏感性分析只检验单个属性对模型的影响程度；而全局敏感性分析则检验多个属性对模型结果产生的总影响，并分析属性之间的相互作用对模型输出的影响[5]。它探索的模型输入空间大，分析结果具有较好的稳健性，因此可以作为直升机火控系统精度敏感性分析的方法。几种常用的全局敏感性分析方法有：回归分析(Regression Analysis, RA)法[6]、傅里叶振幅敏感性检验(Fourier Amplitude Sensitivity Test, FAST)法、响应曲面(Response Surface Methodology, RSM)法[7]、互信息指数(Mutual Information Index, MII)法以及Sobol指数法[8]等。文献[9-10] 对这几种不同的分析法进行了对比分析，并发现Sobol法是进行武器装备敏感性分析的一种较为可行的方法。Sobol法基于模型分解的思想分别得到参数1、2次及更高次的敏感度，可以通过参数对输出方差的贡献比例进行敏感性分级。在处理单个变量或者少许变量的组合时,计算迅速,可操作性强。然而一旦涉及较多变量的组合,该方法的计算量会显著增大,在实际应用中操作较难[11]。此外，它的计算分析是在大量的样本数据基础上开展的，这在很多领域尤其是在军工方面，应用起来会有困难。文献[12-13]分别利用基于 Kriging 模型的建模法和基于响应曲面的建模法建立代理模型，进而基于该模型进行敏感性分析，对Sobol法在一定程度上进行了改进，克服了计算量大、精确分析所需样本量大等缺点。但它们都因对模型有过多的依赖从而面临着如何构建最优代理模型的问题。

将贝叶斯网络(Bayesian Networks, BN)技术应用于系统的敏感性分析，则能很好的弥补上述方法的不足之处。贝叶斯网络能很好地表示变量的随机不确定性和相关性,并能进行不确定性推理，它不但可以实现正向推理,由先验概率推导出后验概率,即由原因导出结果,还可利用公式由后验概率推导出先验概率,即由结果导出原因[14]。最重要的是在很多领域中，当网络参数不存在极端情况，即没有网络参数为0的条件下，贝叶斯网络推理结果的准确度几乎不受其网络参数精度的影响[15]。这给我们在小数据条件下利用贝叶斯网络的推理结果进行系统精度的敏感性分析带来了很大的方便。文献[16-18]将贝叶斯网络应用于电力系统可靠性评估，而文献[19-20]则将其应用于机械系统可靠性评估以及元件的重要度和灵敏度分析中，并且都取得了较好的结果。本文提出运用基于贝叶斯网络和Sobol指数相结合的BNSobol法来进行误差源对火控系统精度影响的全局敏感性分析，利用贝叶斯网络推理的特点，根据先验知识建立贝叶斯网络，通过贝叶斯估计学习网络中相关参数，进而推理得到在各误差源取不同值条件下火控系统精度达到特定等级的概率。最后利用Sobol法方差分解的思想对推理所得概率结果进行处理便可得到各误差源的敏感性系数。相较于其他敏感性分析法而言，BNSobol法在一定程度上减少了对样本量的需求。同时它不依赖于模型，而是直接对数据进行分析。

1 火控系统精度敏感性分析

1.1 精度敏感性定义及问题描述

火控系统精度的敏感性定义为当每个误差源在可能的取值范围内变动时，它们对系统精度的影响程度。将影响程度的大小称为各误差源的敏感性系数，敏感性系数越大，说明该误差源取值的变化对系统精度的影响越大。根据输入指标对输出的影响方式，敏感性系数可分为主效应、全效应、二阶交互效应以及更高阶的交互效应[21]，本文主要研究各误差源对系统精度影响的主效应和二阶交互效应。

火控系统精度敏感性分析的核心目的就是通过对火控系统的误差源进行分析，得到各误差源敏感性系数的大小，在实际应用中根据经验去掉敏感性系数很小的误差源，重点考虑敏感性系数较大的属性。这样就可以大大降低系统的复杂度，减少数据分析处理的工作量，在很大程度上提高了系统的精度，同时可利用各误差源的敏感性系数解决相应的问题。

1.2 火控系统误差源及精度评估指标

影响航炮、火箭弹等无控武器命中精度的主要因素是由火控系统产生的误差， 本文主要研究的误差源如下：传感器(雷达瞄准误差)、惯导(测量误差)、挂架(抖动误差)以及环境误差(随机风、旋翼下洗流)，由于环境误差无法人为控制，故将其取为定值，其他误差则均作为白噪声叠加在标准值上。

本文所考虑误差源间关系如图1所示。

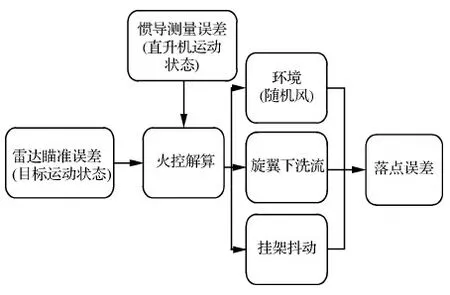
图1 误差源关系图Fig.1 Relation schema of error source

其中，旋翼下洗流采用文献[1]中计算得出的下洗流场。对于随机风场的模拟，则通过文献[22]所建立的数学模型来计算。本文所采用的精度指标为：圆概率偏差(Circular Error Probability, CEP)。定义为弹头落点相对瞄准点散布程度，大小等于以瞄准点为圆心，弹着概率为0.5的圆域半径r[23]。

2 火控系统精度敏感性分析的BNSobol法

2.1 精度敏感性分析的贝叶斯网络模型

针对火控系统精度敏感性分析问题建立如图2 所示的朴素贝叶斯网络。

图2 火控系统精度敏感性分析的朴素贝叶斯网络Fig.2 Native Bayesian network of sensitivity analysis on accuracy of fire control system

根据文献[24]提出以下3点假设：

1) 随机样本D(数据库)是完整的，即在D中没有丢失的数据。

2) 参数矢量相互独立，即

(1)

3) 参数矢量为Dirichle分布，即

(2)

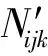
基于上述知识，可以开展贝叶斯网络参数学习：

1) 参数先验分布

(3)

2) 参数的后验分布：

(4)

朴素贝叶斯网络的这一局部独立性(Local Independence)假设有时会与真实情况不一致。如在火控系统精度敏感性分析中，朴素贝叶斯网络的条件独立性假设认为各误差源对系统输出即精度的影响是相互独立的，但火控系统误差源间的交互耦合效应确实是真实存在的。然而，理论分析却表明在许多实际问题中即使此独立性假定与真实情况不一致，朴素贝叶斯学习器仍然具有良好的分类性能[25]。

2.2 基于贝叶斯网络和Sobol指数相结合的BNSobol法

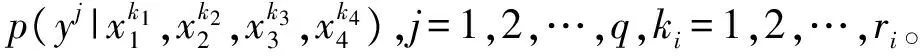
设误差传递函数Y=F(X1,X2,X3,X4)(实际上难以获得具体形式，此处是一种高度的概括，也是为了表述方便)。

1) 主效应分析

V(Y)=E(Y2)-E2(Y)

(5)

(6)

(7)

(8)

VXi(EX-i(Y|xi))=

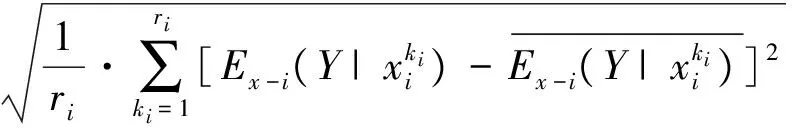
(9)

2) 二阶交互效应分析

E-XiXj(Y|(xixj)k)=

p(yj|(xixj)k,(-xixj)kn)

(10)

式中：(xixj)k为第i个和第j个误差源的第k个取值组合；而(-xixj)kn为除xi和xj外其他误差源的第n个取值组合。

(11)

将式(10)和式(11)代入SXiXj的定义式即可求得Xi与Xj二者的交互效应。

对于Sobol指数法中定义的其他敏感性指标如全效应及其他高阶的交互效应等均可按此思路来进行计算，在此不再赘述。

3 仿真算例及结果分析

3.1 仿真模型

本文主要研究基于航向坐标系[26]直升机火箭弹和航炮对地面目标进行攻击时各误差源对打击精度的影响。其中，直升机机动状态包括平飞和悬停，所采用的火控攻击原理是续连计算命中点(CCIP)。图3所示为水平攻击CCIP瞄准原理。

水平攻击及俯冲攻击瞄准原理与公式等详见文献[27]。

图3 航向坐标系中的水平攻击瞄准图Fig.3 Sight of horizontal attack in course coordinate system

图3中：O为武器投射点；H为攻击瞬间载机的高度；α为载机的俯冲角；W为载机的空速矢量；vCH为瞄准线方位角；μCH为瞄准线俯仰角；A为武器的无风射程矢量；U为风速矢量；T为武器标准下落时间；ε为风向角；C为武器命中点。

3.2 仿真分析总体框架及分析流程

本文仿真分析总体框架分为以下3个模块，如图4所示。

1) 参数生成模块：给定包括环境、目标、载机各参数初始值以及各部分误差的均方差值。

2) 火控解算模块：包括火控解算、武器运动、目标及载机运动。

3) 数据处理模块：根据仿真所得数据计算精度评估指标(CEP)值，进行敏感性分析。

3.3 仿真分析结果

本节中用以下符号代替对应误差源及交互效应：x1为载机偏航角测量误差；x2为挂架随机抖动误差；x3为目标距离测量误差；x4为目标方位瞄准误差。

图4 基于BNSobol法的直升机火控系统精度敏感性仿真分析流程图Fig.4 Simulation analysis flowchart of sensitivity analysis on accuracy of helicopter fire control system based on BNSobol method

限于篇幅，本文仅给出直升机悬停火箭弹对地攻击时的仿真结果。其他攻击状态下的仿真结果与此相似。

3.3.1 基于传统Sobol法分析误差源对火箭弹射击精度的影响

Sobol指数法的灵敏度计算方法包括解析法和蒙特卡洛法，对于输入与输出没有明确表达式的模型主要采用蒙特卡洛计算方法。文献[28]中对该方法进行了详细的叙述，在此不再赘述。初始参数设置见表1。

误差均方差范围设置：x1，x2以及x4的取值范围均为0～0.5，而x3的取值范围为0～2。设各误差均方差值在上述范围内服从均匀分布，采用文献[28]所述方法多次随机抽样不同组数的误差源数据，代入模型仿真计算，可得各误差源对火箭弹命中精度影响的敏感度排序。仿真发现在数据量趋近于5 000组时，分析结果逐渐收敛，限于篇幅，表2～表4仅列出对5 000组数据和500组数据(从5 000组数据中随机抽取)分析所得的各误差源主效应以及二阶交互效应的计算结果。

表 1 初始参数设置Table 1 Setting initial parameters

表2500和5000组数据下各误差源的主效应排序

Table2Orderingsofmaineffectscorrespondingtoeacherrorsourceobtainedunder500and5000datasamples

ErrorSamplesize5000500MaineffectOrderingMaineffectOrderingx10．71610．2083x20．14840．5981x30．20030．5981x40．63220．5032

表35000组数据下各误差源间的二阶交互效应

Table3Twoorderinteractioneffectsbetweenerrorsourcesobtainedunder5000datasamples

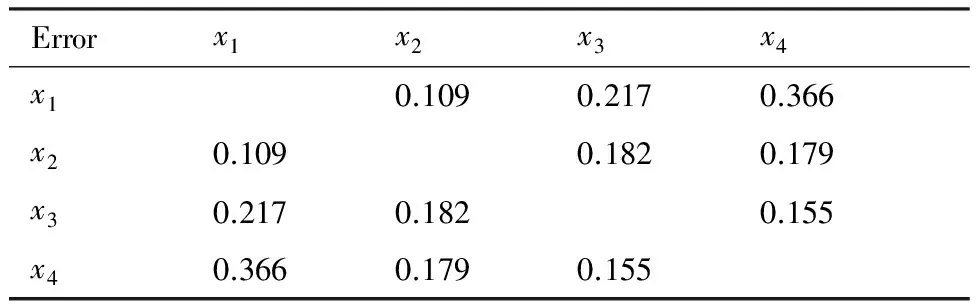
Errorx1x2x3x4x10．1090．2170．366x20．1090．1820．179x30．2170．1820．155x40．3660．1790．155

表4500组数据下各误差源间的二阶交互效应

Table4Twoorderinteractioneffectsbetweenerrorsourcesobtainedunder500datasamples

Errorx1x2x3x4x10．25100．04800．1755x20．25100．43800．2950x30．04800．43800．4025x40．17550．29500．4025

3.3.2 基于BNSobol法分析误差源对火箭弹射击精度的影响

初始参数设置同3.3.1节。贝叶斯网络的建立如2.1节所述。在进行分析之前先对输入与输出作相应的处理。

1) 输入离散化

由于直升机火控系统中各部件的误差均方差往往并非某一确定值，而是在某一区间取值，故将各误差源取值离散化为如表5所示的区间。

表5 各误差源的取值区间Table 5 Value interval for each error source

2) 输出处理

按CEP大小将精度指标划分为两个等级：当圆概率偏差小于3 m时精度等级为1，当圆概率偏差大于3 m时精度等级为2。

在上述处理的基础上，从3.3.1节基于传统Sobol法进行敏感性分析时所产生的5 000组数据中多次随机抽取不同组数仿真样本数据，根据式(3)和式(4)借助MATLAB贝叶斯网络工具箱(Bayesian Netorks Toolbox, BNT)进行参数学习，发现在数据量大于400时，结果逐渐收敛。故下文所列结果均是在3.3.1节所产生的500组数据下分析得到的。表6中的数据即为网络参数θijk，其中j指精度等级，j=1表示精度等级为1，即CEP小于3 m；j=2表示精度等级为2，即CEP大于3 m；k指各误差源的取值区间。例如：表中第一行第一列的数据0.18指在精度等级为1时，误差源X1的取值在区间(0～0.05)内的概率。

从表6可以看出网络中各参数值并非呈现单调递增或递减关系，这说明原始数据中各误差源间存在交互耦合效应。由学习到的参数进行推理便可获得与256种误差源取值组合对应的毁伤概率，进而根据2.2节所述方法可得各敏感性指标值，具体结果见3.3.3节。如引言所述，利用该方法还可以进一步得到使总体效能达到最优的各误差源的具体取值区间。由于贝叶斯网络中所得结果都是以概率的形式表示的，故假定推理所得CEP小于3 m的概率超过0.75时即认为可以满足精度要求，从而由全部256种组合中筛选出满足条件的16组，见表7。表7中每一列的数据代表4个误差源的一种取值区间组合，其具体值对应于表5，如最后一组数据表示x1,x2,x3,x4的取值区间分别为(2，2，4，1)。将16组误差源取值代回仿真模型验证得CEP小于3 m的概率均在0.75以上，由此验证了推理的准确性。

表6 网络参数学习结果Table 6 Learning result of network parameters

表7 满足精度要求的误差源取值区间组合Table 7 Value interval combinations of error sources subject to accuracy requirement

3.3.3 两种精度敏感性分析法的分析结果对比

图5和图6为综合3.3.1和3.3.2两节的敏感性计算结果后得到的两种敏感性分析法计算所得各误差源主效应以及误差源间二阶交互效应的对比。

1) 从分析结果对比图可以看出两种分析方法所得结果尽管并非完全吻合，但均可得出如下两点结论：① 在多误差源同时作用于火控系统时，载机偏航角测量误差和目标方位瞄准误差值的变动对火箭弹射击精度有重要影响，是主要误差源；② 各误差源间均存在着较强的二阶交互效应，其中载机偏航角测量误差和目标方位瞄准误差两者间的交互效应最为显著，在分配误差时应重点关注它们二者的组合。

2) Sobol法统计分析需要大量的样本数据，这在实际应用中有时很难做到。以本文的直升机火控系统精度分析为例，在数据量充分时，即提供5 000组数据情况下Sobol法能分析得到正确的结论。而当数据量不充分时，即只提供500组数据，则传统Sobol法分析所得结果变得不再准确。此处仅对4种误差源进行了分析，当误差源增多或模型更为复杂时，Sobol法所需的样本量极速增长，因此该方法应用起来显然变得十分困难。但BNSobol法在仅有500组数据时分析得出了与准确值近似的结果，因此大大减少了工程试验成本。

图5 两种分析法所得各误差源的主效应对比Fig.5 Comparison of main effect corresponding to each error source obtained by two analytical methods

图6 两种分析法所得各误差源间的二阶交互效应对比Fig.6 Comparison of two order interaction effect between error sources obtained by two analytical methods

3) Sobol法只能定性的给出各误差源的敏感性区间，作为缩小取值区间的参考。而由3.3.2节分析知BNSobol法通过对输入及输出数据进行离散化处理可以给出满足约束条件的各误差源具体取值区间的组合，即可在系统设计阶段为研究人员提供定量依据从而实现对系统总体精度的有效控制。

3.3.4 BNSobol法的有效性分析

为考察本文提出的BNSobol法在不同网络结构下分析计算的有效性，取不同数量的误差源分别加入到系统中并利用BNSobol法进行误差源的敏感性分析。以传统Sobol法在充分数据下计算所得各敏感性指标值为准，考察不同网络结构下BNSobol法计算所得各误差源敏感性指标值的平均精度。

图7 BNSobol法在不同网络结构下对各误差源主效应值计算的平均精度Fig.7 Average precision of main effects for each error source solved by BNSobol method under different network structures

4 结 论

针对现有火控系统精度研究大都基于单因素变量展开的情况，提出应进行多变量的敏感性分析。对典型的全局敏感性分析法及其相应的改进方法进行了分析，针对它们存在的缺陷与不足，提出一种全局敏感性分析新方法，即BNSobol法，通过将贝叶斯网络和传统Sobol指数法相结合来进行敏感性分析。根据直升机特点建立了火控对地攻击仿真模型，选取实际作战中影响较为重要的典型部件作为误差源。最后分别运用传统Sobol指数法和BNSobol法对直升机火控系统精度进行了全局敏感性分析。

对比分析发现BNSobol法存在如下几点优越性：① 不依赖于模型；② 分析得到满足精度要求的结果所需的数据量较小；③ 不仅能给出各误差源的敏感区间，还能根据特定约束条件确定出其具体取值区间。该方法可为直升机火控系统设计研究时如何分配各模块误差大小从而提高总体精度或效费比提供参考和理论支持。

本文的工作初步将贝叶斯理论与Sobol指数法相结合，实现了小数据下对直升机火控系统进行精度的敏感性分析。然而算法的精度仍有待提高，在未来的工作中拟对贝叶斯网络推理算法进行深入研究，寻求提高算法整体精度的途径。

[1] 周克栋, 李自勇, 赫雷, 等. 弹箭在直升机旋翼下洗流场作用下运动规律研究[J]. 兵工学报, 2003, 24(2): 204-208.

ZHOU K D, LI Z Y, HE L, et al. A study on the movement of rocket under down-wash flow of a helicopter’s rotor[J]. Acta Armamentarii, 2003, 24(2): 204-208 (in Chinese).

[2] 魏靖彪, 薛晓中. 悬停旋翼下洗流对导弹的气动特性和初始弹道的干扰研究[J]. 空气动力学学报, 2005, 23(2): 217-221.

WEI J B, XUE X Z. Aerodynamic characteristics and initial ballistic interference on a missile by a helicopter’s rotor down-wash in hovering[J]. Acta Aerodynamica Sinica, 2005, 23(2): 217-221 (in Chinese).

[3] 曹林平, 黄长强. 武装直升机无控武器射击误差源分析[J]. 火力与指挥控制, 2000, 25(1): 70-73.

CAO L P, HUANG C Q. Analysis for error source causing fire error of non-control weapon of armed helicopter[J]. Fire Control and Command Control, 2000, 25(1): 70-73 (in Chinese).

[4] ASCOUGH II H C, GREEN T R, MA L, et al. Key criteria and selection of sensitivity analysis methods applied to natural resource models[C]//Modsim International Congress on Modeling and Simulation, Modeling, 2005: 2463-2469.

[5] 蔡毅, 邢岩, 胡丹. 敏感性分析综述[J]. 北京师范大学学报: 自然科学版, 2008, 44(1): 9-16.

CAI Y, XING Y, HU D. On sensitivity analysis[J]. Journal of Beijing Normal University: Natural Science, 2008, 44(1): 9-16 (in Chinese).

[6] TONDEL K, VIK J O, MARENS H, et al. Hierarchical multivariate regression-based sensitivity analysis reveals complex parameter interaction patterns in dynamic models[J]. Chemometrics & Intelligent Laboratory Systems, 2013, 120(10): 25-41.

[7] ZHAO J, YAN S, WU J. Analysis of parameter sensitivity of space manipulator with harmonic drive based on the revised response surface method[J]. Acta Astronautica, 2014, 98(5): 86-96.

[8] SOBOL I M. Sensitivity estimates for nonlinear mathematical models[J]. Matem Mod, 1990, 2(1): 112-118.

[9] SUMEET R, PATIL H, CHRISTOPHER F. Comparison of sensitivity analysis methods based on applications to a food safety risk assessment model[J]. Risk Analysis, 2004, 24(3): 573-585.

[10] 罗鹏程, 傅攀峰. 武器装备敏感性分析方法综述[J]. 计算机工程与设计, 2008, 29(21): 5546-5549.

LUO P C, FU P F. Review on weapons and equipment sensitivity analysis methods[J]. Computer Engineering and Design, 2008, 29(21): 5546-5549 (in Chinese).

[11] RATTO M, PAGANO A, YOUNG P. State dependent parameter metamodelling and sensitivity analysis[J]. Computer Physics Communications, 2007, 177(11): 863-876.

[12] 张晓航, 雷刚, 石景岚, 等. 基于Kriging模型的武器装备体系效能分析[J]. 舰船电子工程, 2012, 32(10): 31-33.

ZHANG X H, LEI G, SHI J L, et al. Effectiveness analysis of weapon system-of-systems based on kriging model[J]. Ship Electronic Engineering, 2012, 32(10): 31-33 (in Chinese).

[13] 孔凡哲, 宋晓猛, 占车生, 等. 水文模型参数敏感性快速定量评估的RSMSobol方法[J]. 地理学报, 2011, 66(9): 1270-1280.

KONG F Z, SONG X M, ZHAN C S, et al. An efficient quantitative sensitivity analysis approach for hydrological model parameters using RSMSobol method[J]. Acta Geographica Sinica, 2011, 66(9): 1270-1280 (in Chinese).

[14] 尹晓伟, 钱文学, 谢里阳. 贝叶斯网络在机械系统可靠性评估中的应用[J]. 东北大学学报: 自然科学版, 2008, 29(4): 557-560.

YIN X W, QIAN W X, XIE L Y. Application of bayesian network to reliability assessment of mechanical systems[J]. Journal of Northeastern University: Natural Science, 2008, 29(4): 557-560 (in Chinese).

[15] AGNIESZKA O, MAREK J, DRUZDZEL. Impact of precision of bayesian network parameters on accuracy of medical diagnostic systems[J]. Artificial Intelligence in Medicine, 2013, 57(3): 197-206.

[16] YU D C, NGUYEN T C, HADDAWY P. Bayesian network model for reliability assessment of power systems[J]. IEEE Transactions on Power Systems, 1999, 14(2): 426-432.

[17] 霍利民, 朱永利, 范高峰, 等. 一种基于贝叶斯网络的电力系统可靠性评估新方法[J]. 电力系统自动化, 2003, 27(5): 36-40.

HUO L M, ZHU Y L, FAN G F, et al. A new method for reliability assessment of power system based on bayesian networks[J]. Automation of Electric Power Systems, 2003, 27(5): 35-40 (in Chinese).

[18] 霍利民, 朱永利, 张在玲, 等. 贝叶斯网络在配电系统可靠性评估中的应用[J]. 电工技术学报, 2004, 19(8): 113-118.

HUO L M, ZHU Y L, ZHANG Z L, et al. Bayesian networks application to reliability evaluation of electric distribution systems[J]. Transactions of China Electro-Technical Society, 2004, 19(8): 113-118 (in Chinese).

[19] 尹晓伟, 钱文学, 谢里阳. 系统可靠性的贝叶斯网络评估方法[J]. 航空学报, 2008, 29(6): 1482-1489.

YIN X W, QIAN W X, XIE L Y. A method for system reliability assessment based on bayesian networks[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(6): 1482-1489 (in Chinese).

[20] 尹晓伟. 基于贝叶斯网络的元件重要度和灵敏度分析[J]. 沈阳工程学院学报： 自然科学版, 2012, 8(3)： 4-7.

YIN X W. Elements importance and sensitivity analysis based on bayesian network[J]. Journal of Shenyang Institute of Engineering: Natural Science, 2012, 8(3)： 4-7 (in Chinese).

[21] SALTELLI A. Sensitivity analysis in practice: a guide to assessing scientific models[J]. Journal of the American Statistical Association, 2006, 101(473): 398-399.

[22] 王欣, 张凤阁, 姚俊, 等. 蒙特卡罗法分析随机风对火箭弹落点散布的影响[J]. 弹箭与制导学报, 2009, 29(1): 198-201.

WANG X, ZHANG F G, YAO J, et al. Analyze effect of random wind on shell distribution of rocket using Monte-Carlo method[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2009, 29(1): 198-201 (in Chinese).

[23] 魏诗卉, 王明海. 导弹作战使用命中精度CEP评定方法研究[J]. 飞行力学, 2005, 23(4): 52-55.

WEI S H, WANG M H. Research on the missile operational use CEP assessment method[J]. Flight Dynamics, 2005, 23(4): 52-55 (in Chinese).

[24] HECKERMAN D. Bayesian networks for data mining[J]. Data Mining & Knowledge Discovery, 1997, 1(1): 79-119.

[25] DOMINGOS P, PAZZANI M. Beyond independence: conditions for the optimality of the simple bayesian classifier[J].Machine Learning, 1996, 29: 105-112.

[26] 高晓光. 航空军用飞行器导论[M]. 西安: 西北工业大学, 2004: 93-115.

GAO X G. Introduction to aviation military aircraft[M]. Xi’an: Northwestern Polytechnical University Press, 2004: 93-115 (in Chinese).

[27] 陆彦. 航空火力控制技术[M]. 西安: 西北工业大学出版社, 1989: 24-50, 221-226， 296-304.

LU Y. Aviation fire control technology[M]. Xi’an: Northwestern Polytechnical University Press, 1989: 24-50, 211-226, 296-304 (in Chinese).

[28] SALTELLI A. Global sensitivity analysis: the primer[M]. New Jersey: John Wiley & Sons, 2008: 164-167．

贺楚超男， 博士研究生。主要研究方向： 贝叶斯网络学习与应用。

Tel: 029-85269057

E-mail: xomrssh@163.com

高晓光女， 博士， 教授， 博士生导师。主要研究方向： 智能决策， 复杂系统建模与效能分析。

Tel: 029-88431256

E-mail: cxg2012@nwpu.edu.cn

URL： /www.cnki.net/kcms/detail/11.1929.V.20160530.1450.002.html

Sensitivityanalysisonaccuracyofhelicopterfirecontrolsystem:ABNSobolmethod

HEChuchao,GAOXiaoguang*

SchoolofElectronicsandInformation,NorthwesternPolytechnicalUniversity,Xi’an710129,China

Pointingatthestatusthatmostofthecurrentresearchonlyanalyzedtheeffectthatasingleerrorsourceworksonthehelicopterfirecontrolsystem,weproposethatthesensitivityanalysisonaccuracyofthehelicopterfirecontrolsystemshouldbeexecuted.Toachievemoreaccuratesensitivityanalysiswithsparsedataandimprecisemodel,anewsensitivityanalysismethodnamedBNSobolmethodisproposedbasedonBayesiannetworkandSobolindextheory.TheproposedBNSobolmethodisexperimentallycomparedwithclassicalSobolmethod.Experimentsrevealthattheproposedmethodcanreducetheamountofrequiredanalysisdata,meanwhilesubjecttocertainaccuracy.Theanalysisdoesnotrelyonthemodelanditcanpresentconcreteerrorsource’svalueregionundercertainconstraints.TheBNSobolmethodprovidestheorysupportandalternativemethodforerrorallocationtoeachpart,whichfurtherraisestotalefficacyofthehelicopterfirecontrolsystem.

helicopter;accuracyanalysis;sensitivityanalysis;firecontrolsystem;Bayesiannetwork

2015-10-22；Revised2016-02-15；Accepted2016-05-16；Publishedonline2016-05-301450

NationalNaturalScienceFoundationofChina(61573285)

.Tel.：029-88431256E-mailcxg2012@nwpu.edu.cn

2015-10-22；退修日期2016-02-15；录用日期2016-05-16； < class="emphasis_bold">网络出版时间

时间：2016-05-301450

www.cnki.net/kcms/detail/11.1929.V.20160530.1450.002.html

国家自然科学基金 (61573285)

.Tel.：029-88431256E-mailcxg2012@nwpu.edu.cn

贺楚超， 高晓光． 直升机火控系统精度敏感性分析的BNSobol法J． 航空学报,2016,37(10):3110-3120.HECC,GAOXG.SensitivityanalysisonaccuracyofhelicopterfirecontrolsystemABNSobolmethodJ.ActaAeronauticaetAstronauticaSinica,2016,37(10):3110-3120.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0151

V233.7

A

1000-6893(2016)10-3110-11