一种复杂空间飞网系统参数优化设计方法
2016-11-20王晓慧万长煌夏人伟
王晓慧, 万长煌, 夏人伟
北京航空航天大学 宇航学院, 北京 100083
一种复杂空间飞网系统参数优化设计方法
王晓慧*, 万长煌, 夏人伟
北京航空航天大学 宇航学院, 北京 100083
由轻质软绳索编织而成的空间飞网是为非合作目标捕获而提出的空间系统概念,在空间碎片和废弃航天器处理方面具有很大的应用潜力。从平台抛射出后,飞网在空间形成不稳定的网形,且网形变化规律受初始参数设计的影响较大。针对空间飞网系统设计与试验中系统参数匹配问题,本文提出以容错值作为飞网展开性能的定量描述,从捕获任务的层面,建立面向捕获容错的空间飞网系统参数优化数学模型;以抓捕固定距离、确定大小的目标任务为算例,联合Isight优化平台与ANSYS/LS-Dyna求解,得到飞网系统最优参数匹配,算例仿真结果表明结果的适用性;最后,利用试验设计和极差分析方法验证最优点的稳定性。研究的模型与方法为开展空间飞网系统地面及空间试验等工程应用提供理论依据。
空间飞网系统; 参数匹配; 优化模型; 容错值; 实验设计
随着人类对空间资源的开发与利用,空间废弃卫星和轨道碎片对在轨航天器的安全影响日渐严重[1-4]。2001年,欧空局提出利用绳系飞网捕获地球静止轨道卫星的ROGER(Robotic Geostationary Orbit Restorer)计划,以解决地球静止轨道资源日趋紧张的问题[5-6]。应用飞网系统来捕获空间非合作目标是一种新兴的在轨捕获技术概念[7-9]。
与机械臂为代表的刚性捕获相比,飞网捕获具有安全性高、对载体航天器影响小、能耗低等优点,在航天器回收、轨道清理等领域有着巨大的应用潜力[10-11]。
对于空间飞网捕获,较多的研究集中于飞网捕获总体规划[12-17]以及捕获系统绳系动力学建模与控制方面[18-25],针对飞网形态变化及系统参数优化的研究较少[26-27]。空间飞网在发射展开与抓捕过程中,网的柔性绳索可能经历多次的松弛和张紧的状态变化,网的空间位形也随之改变,其运动变形属于复杂的物体运动[28-30]。研究这类问题主要通过数值仿真和大量的物理试验两种方法[30-31]。由于空间飞网应用于轨道微重力环境,所需试验条件在地面难以实现,试验成本也限制了可开展试验的次数。同时,设计空间大、设计经验较少也使得试验参数匹配问题困难。数值仿真则利用成熟的有限元软件或自编程序对空间飞网抛射展开过程进行模拟与分析,计算机仿真的灵活性和低成本使得其在空间飞网的研究与设计中更具优势。在这方面,国内外对空间飞网捕获的研究主要集中于柔性网动力学建模和有限元仿真模型的细化[31-34]。基于仿真的优化设计研究多采取在单维空间中寻优,未考虑全设计变量空间寻优问题。
本文主要基于飞网有限元仿真,针对空间飞网发射展开过程,通过对比在指定位置处飞网网口展开面积与目标最大包络球的截面面积,构造出容错值函数,用以描述飞网展开捕获性效果,并以容错值为优化目标,构建了空间飞网参数优化的数学模型,通过计算分析优化算例,验证了空间飞网优化建模方法与模型的有效性,同时说明了针对抓捕一定距离的空间目标,飞网系统的牵引块质量、发射速度、发射角度存在最优匹配。本文对空间飞网系统参数的优化建模与方法可为空间飞网系统设计与试验提供理论依据。
1 空间飞网捕获系统
空间飞网捕获系统为同轴式发射器,主要部分为4个牵引块、网箱和飞网,如图 1所示。网箱固定于载体航天器上,飞网放置在网箱中,飞网为l×l的正方形斜编织平网,飞网的牵引块通过短绳索与平网的4个角相连,见图 2,绳网中心与载体航天器通过系绳连接。
飞网采用直接抛射展开发射方式,即牵引块以一定的初速度发射,将飞网从网箱中拉出、张开并飞向抓捕目标。空间飞网的展开过程是高柔性系统复杂的动力学行为,为便于仿真与分析,作几点假设:① 载体航天器与抓捕目标相距较近,忽略捕获过程的轨道高度、载体航天器姿态等的变化;② 载体航天器和抓捕目标的相对速度近似等于0;③ 空间飞网的飞行过程中,系绳的牵引阻力忽略不计;④ 飞网飞行过程中,牵引块近似成质点,不考虑其姿态的变化;⑤ 忽略飞网发射过程中的摩擦与接触。
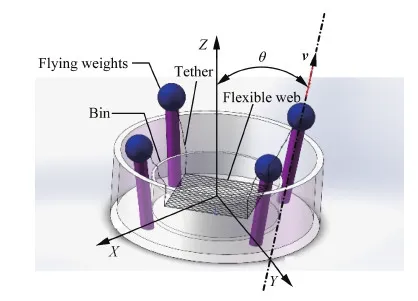
图1 同轴式飞网发射器示意图Fig.1 Schematics of equipment to coaxially launch space web
建立了空间飞网捕获坐标系OXYZ,如图3所示,其中原点为网收容筒的中心,Z轴沿发射器轴向,并指向抓捕目标,X轴指向地球,Y轴满足右手定则。牵引块的发射方向通过其初始速度矢量v与Z轴的夹角θ来描述。

图2 飞网构型Fig.2 Configuration of plane web

图3 空间飞网捕获坐标系OXYZFig.3 Capturing coordinate system of space web OXYZ
2 空间飞网系统展开仿真
飞网由柔性绳索编织而成,而绳索在受力上不同于刚体和小变形体,绳索可以分成两种状态,即张紧与松弛,对应不同受力特性:在松弛状态下,网绳不能承受任何外力作用;在张紧状态下,绳索只能承受拉力作用,而不能承受压力、弯矩和扭矩作用[35-36]
2.1 有限元模型
基于ANSYS/LS-Dyna有限元软件进行空间飞网展开的建模与仿真分析,选取ANSYS单元库中的Link167模拟柔性绳索,Link167可设置绳索的松弛量,且在三维空间各个方向上具有良好的动力学特性。单元受力定义式为
F=Kmax(Δl,0)
(1)
式中:Δl为单元长度的改变量;K为单元刚度。Δl和K分别可通过式(2)和式(3)计算得到。
Δl=lt-(l0-δ)
(2)

(3)
式中:l0为绳索单元初始长度;lt为绳索单元两端节点当前距离;δ为绳索单元初始偏移量,初始时刻,假定绳索均处于松弛状态,初始偏移量应设置δ≤0;E为绳索单元材料的弹性模量;Asection为绳索单元截面积。通过上述定义可知,所定义的Link167单元可有效地模拟绳索松弛与张紧两种力学状态。
同时,由于不考虑牵引质量块的姿态,选择集中质量单元MASS166模拟,减少系统的自由度,降低计算复杂度。空间飞网结构及材料参数如表1 所示。

表1 空间飞网结构及材料参数Table 1 Structural and material parameters of space web
仿真中,结构阻尼μ由等效阻尼系数α和β替代,阻尼定义式为
C=αM+βK
(4)
式中:M为飞网质量矩阵;K为飞网刚度矩阵;α和β为系统阻尼系数。由文献[37]可知,对无连接绳的柔性模型,等效阻尼系数β会影响展开速度以及最大展开面积,根据参考文献结果,设置仿真等效阻尼系数α=0、β=0.1。
2.2 发射展开过程仿真分析
设置仿真分析中牵引块的发射速度大小为v=20 m/s,发射角度θ=30°。设置总仿真时间为18 s,仿真步长设置为0.01 s。
经过仿真,飞网直接抛射过程可以分成3个阶段,如图 4(a)~图 4(c)所示:阶段Ⅰ是发射阶段,即4个牵引块以设计速度与角度飞出,开始将网的4个角点拉离网箱,此时部分绳网还在网箱中;阶段Ⅱ是网面展开阶段,即牵引块飞出一段距离,飞网全部脱离网箱,网形呈现出四棱锥体,网口面积逐渐增大并达到峰值;阶段Ⅲ为网面收缩阶段,即当网口面积达到峰值后,牵引块受拉回弹,绳网网口收缩。
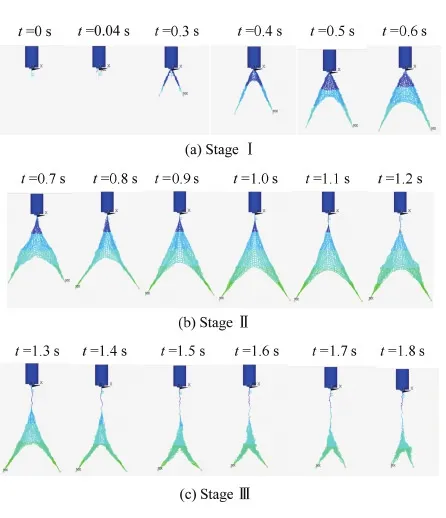
图4 空间飞网直接抛射过程网形变化的3个阶段Fig.4 Three stages in space web casting process
由于绳索网在飞行过程中,网面拉伸,属于质量分布系统,通过牵引块的位移定义飞网的飞行距离Sspaceweb,其表达式为
(5)
式中:ri(i=1,2,3,4)分别为4个牵引块在捕获坐标系中的位置矢量。
由上述定义可得,空间飞网展开过程中,绳网飞行距离Sspaceweb随时间的变化如图 5所示,可知在0~1.2 s,牵引块飞出,绳网飞行距离接近线性增大,达到最大飞行距离约为17 m;1.2 s之后,系统动量在牵引块、绳网和系绳之间传递,牵引块速度减小并反向,定义的绳网网口飞行距离也逐渐减小。
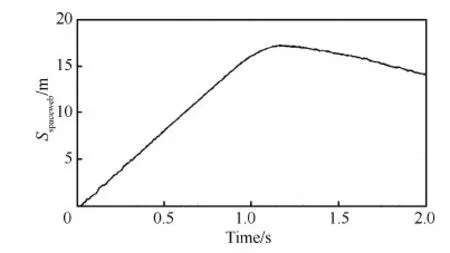
图5 空间飞网飞行距离随时间的变化曲线Fig.5 Graph of Sspaceweb as a function of time
2.3 飞网展开性能指标
空间飞网应用于在轨捕获时,不同的捕获目标对空间飞网的展开性能有着不同的要求。通过对空间飞网展开过程中的尺寸、形状变化进行定量描述,用于评价飞网的展开性能。对于距离和大小可测的目标,如废弃的轨道飞行器,需要空间飞网在指定的距离附近展开网形最佳,如网口面积展开到最大值;对于尺寸小、在一定的空间区域分布的目标,如空间碎片,则需要空间飞网维持一定的网形飞过目标的分布区域[29,36]。
针对捕获距离和目标外包络尺寸可测的抓捕任务,对空间飞网的总体参数综合优化研究,需要重点考虑的指标有两点:飞网展开网口面积和飞网展开网四边中点矩形面积,见图 6,其中,AQ为飞网展开网口面积,是指在飞网展开过程中,4个牵引块所构成四边形的面积;AE为飞网展开四边中点矩形面积,是指在飞网展开过程中,过4个网边中点的四边形面积;AT为目标外包络球的最大截面积。
根据上述定义,在前文的展开仿真中,空间飞网网口展开面积AQ和飞网展开网边中点四边形面积AE随时间的变化分别如图 7的虚线和实线所示,0~2 s中,AQ先快速增大到峰值而后急剧减小。绳网第一次展开过程中,AE都不大于AQ。而且AE整体变化略滞后于AQ,要抓捕目标,要求AQ要大于AT。
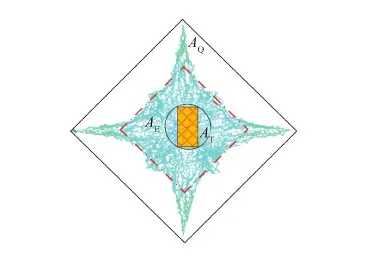
图6 飞网展开性能指标示意图Fig.6 Performance indexes of unfolded space web
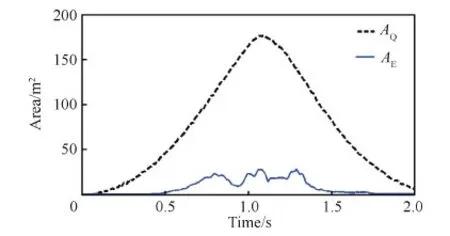
图7 空间飞网展开面积随时间的变化曲线Fig.7 Curves of space web unfolding areas over time
3 空间飞网系统参数优化
3.1 优化模型
3.1.1 优化设计变量
在空间飞网系统中,设计参数可以分为任务参数、飞网结构参数和飞网发射参数3类。其中,任务参数主要包括捕获目标的外包络球的尺寸和目标的距离等;飞网的结构参数主要包括飞网的网面大小、网格数目、网格疏密,还有牵引块的质量和网舱盖的质量等;飞网的发射参数主要包括牵引块的发射速度大小和角度等。
对于捕获一定距离和一定大小的目标,总体参数一般作为顶层设计变量,赋予确定值。选取飞网系统结构参数中的牵引块质量m和飞网发射参数中牵引块发射速度大小v与角度θ作为设计变量X=[mvθ]T,m∈[minf,mup],v∈[vinf,vup],θ∈[θinf,θup],3个设计变量都是连续变量,其中上标“up”和“inf”分别表示取值上下限。
3.1.2 优化目标
理想的抛射过程中,飞网应当在较短时间内展开到充分大的面积,并保持较好的网型飞行较长时间和较远距离,以满足时间和空间上的容错性要求[28-29]。而实际情况中,网面在张开之后会出现收缩回弹,使得网面很难长时间或长距离维持。同时,抓捕相隔距离及目标大小可测的轨道目标,更需关注在飞向目标的过程中,网绳是否发生缠绕以及达到目标所在位置时网口展开面积的大小。
基于上述分析,可定义容错值(Error Tolerance,ET)描述空间飞网在指定位置L捕获的容错,其值由式(6)给出。
(6)
3.1.3 优化约束
优化约束可以分为两部分:① 基于建模假设物理规律的约束条件,如动量守恒定律和绳索强度约束;② 基于工程需求与仿真分析而引入的约束方程,如系统总质量约束以及飞网展开网口面积与飞网展开四边中点矩形面积的约束。以下将对这些约束逐一说明。
1) 基于前文定义的建模假设,忽略了重力、轨道摄动等系统外力,空间飞网发射过程动量守恒,因而存在的等式约束为
h(X)=p(t)-p(0)=0
(7)
式中:p(0)为初始时刻系统的动量;p(t)为发射后t时刻系统的动量。由于仿真分析采用LS-Dyna的显式动力学模块求解,瞬态分析过程此约束均满足。
2) 飞网应用于空间捕获,其系统的总质量有设计上限,可表示为如式(8)所示的不等式约束。
g1(X)=4m+mweb-mup≤0
(8)
式中:m为单个牵引块的质量;mweb为绳网的质量;mup为绳网系统质量上限。
3) 由2.3节的分析可知,在网口面积第1次收缩过程中,AE会出现大于AQ的情况。因而,可以定义AE (9) (10) 式中:εL为计算飞网飞行距离与L的允许偏差。需要指出的是,在到达L前的每一个时间步都需要计算约束式(9),所以此约束函数具体个数由定义的目标距离以及分析的时间步长决定。式(9)中约束函数采用指数函数定义可避免因AE太小且AE与AQ相差太大而导致约束函数值趋向于无穷。 4) 绳索采用尼龙材料,在飞网展开过程中会受到轴向拉力作用,因而存在绳索的强度约束为 (11) 式中:Fmax为所有绳索在飞行过程中,即t∈[0,tL]的轴向最大拉力;[σb]为绳索材料许用拉应力。 综上所述,可建立空间飞网系统参数优化模型为 (12) 式中:m∈[minf,mup],v∈[vinf,vup],θ∈[θinf,θup];mc和vc分别为飞网中心点处的集中质量和速度。 3.2 优化算例 3.2.1 算例说明 设定目标距离捕获平台L=30 m,目标的最大展长D=10 m,即AT=πD2/4=25π m2,飞网大小为20 m×20 m,网格密度为40×40。绳索材料是尼龙,弹性模量E=2 GPa,密度为ρ=970 kg/m3,许用最大拉应力[σb]=30 MPa。定义设计变量m的取值范围为0.5~5.0 kg,牵引块发射速度大小v的取值范围为2 ~40 m/s;牵引块发射角度θ的取值范围为15°~60°。则优化模型式(12)可改写为 (13) 式中:m∈[0.5,5.0] kg,v∈[2,40] m/s,θ∈[15°,60°] 3.2.2 优化结果及验证 针对模型式(13),本文用自适应模拟退火(Active Simulated Annealing,ASA)算法和序列二次规划(Sequential Quadratic Programming, SQP)算法混合优化策略对优化模型进行解算[38-39]。 图8为全局算法ASA优化目标容错值ET的迭代曲线图,ASA优化算法计算120次,耗时约10 h 30 min,优化中初始设计点由ASA算法随机生成,其为X0=[mvθ]T=[1.75 kg33.85 m/s 23.45°]T,随机初始设计的容错值ET0=1.978 5,即在L=30 m处,飞网网口展开面积AQ0=247.25 m2,大于目标的外包络圆的面积AT=78.54 m2。 图8 自适应模拟退火(ASA)优化迭代曲线Fig.8 Iterations of optimization using active simulated annealing (ASA) 图9 SQP优化迭代曲线Fig.9 Iterations of optimization using SQP 提取仿真过程绳索单元的轴向力,最大轴向力Fmax=15.95 N出现在第613号Link167单元的t=5.16 s时刻,校核绳索的强度约束为 (14) 可知,飞网展开过程绳网正应力满足约束要求。 综上所述,对空间飞网系统总体参数优化设计计算总耗时约为25 h,其中,全局寻优用时约为10 h 40 min,局部寻优耗时约为4 h 10 min。将最终的优化结果圆整得最优设计点X*=[mvθ]T=[4.20 kg 7.20 m/s 28.5°]T,计算出容错值ET*=2.229。 图10 3个设计点Xs、X0和X*对应的飞网展开面积AQs、AQ0和随飞行距离Sspaceweb的变化曲线Fig.10 Curves of space web extending areas AQs, AQ0 and vs Sspaceweb,which correspond to three design points Xs, X0 and X* 3.2.3 优化结果稳定性分析 在最优设计点X*处设计3因素4水平的正交试验,见表2,因素水平均以最优点为基准上下浮动5%和2%。选取L16(43)正交表,进行表头设计将各因素放入各列,如表3所示,经过16次有限元仿真分析,各响应值结果也列入表3。 利用极差分析法研究最优点附近目标值对各参数的敏度。计算各参数的极差,由表 3的结果可知,在最优点X*处,设计变量上下浮动5%,容错值ET变化0.8%,目标值较稳定。且在最优值附近,设计变量中,发射角度对目标的敏度值最大,发射速度与牵引块质量敏度值相差不大。 表2 正交试验因素与水平Table 2 Factors and levels in cross test 表3 L16(43)正交试验及仿真结果Table 3 L16(43) cross test and results of simulations 1) 基于ANSYS/LS-Dyna完成了空间飞网参数化建模与直接抛射展开过程的仿真,分析了飞行过程中,柔性网形状随时间和飞行距离的变化规律,并提出了飞网展开性能的指标。 2) 联合Isight与ANSYS/LS-Dyna仿真,实现了全设计变量空间的优化设计。通过对捕获任务的分析,引入容错值定义,以表征飞网展开面积与目标体包络相对大小,对飞网抓捕效果、飞网抓捕的成功率与可靠性描述更加准确。在此基础上提出了针对捕获指定距离、以容错值为优化目标函数的优化模型,并利用算例验证了优化模型的准确性和方法的可行性。 3) 本文建立的优化模型可适用于空间飞网捕获不同距离、不同大小目标的性能描述,研究结果为飞网系统设计时参数最优匹配以及精度控制提出了相应参考,为在轨捕获与碎片清理任务提供理论依据。 [1] ANDERSON P V, SCHAUB H. Local orbital debris flux study in the geostationary ring[J]. Advances in Space Research, 2013, 51(12): 2195-2206. [2] KLINKRAD H, BENDISCH J, BUNTE K D, et al. The MASTER-99 space debris and meteoroid environment model[J]. Advances in Space Research, 2001, 28(9): 1355-1366. [3] YATES J M, SPANBAUER B W, BLACK J T. Geostationary orbit development and evaluation for space situational awareness[J]. Acta Astronautica, 2012, 81(1): 256-272. [4] SCHAUB H, MOORER D F, Jr. Geosynchronous large debris reorbiter: Challenges and prospects[J]. The Journal of the Astronautical Sciences, 2012, 59(1-2): 161-176. [5] TIBERT G, GARDSBACK M. Space webs final report: ACT-RPT-MAD-ARI-05-4109a[R]. Sweden: Advanced Concepts Team, ESA, 2006. [6] MCKENZIE D, CARTMELL M, RADICE G, et al. Space webs final report:ACT-RPT-MAD-ARI-05-4109[R]. Sweden: Advanced Concepts Team, ESA, 2006: 2-10. [7] 李新刚, 裴胜伟. 国外航天器在轨捕获技术综述[J]. 航天器工程, 2013, 22(1): 113-119. LI X G, PEI S W. On-orbit capture technology of spacecaft[J]. Space Engineering, 2013, 22(1): 113-119 (in Chinese). [8] 崔乃刚, 王平, 郭继峰, 等. 空间在轨服务技术发展综述[J]. 宇航学报, 2007, 28(4): 805-811. CUI N G, WANG P, GUO J F, et al. A review of on orbit servicing[J]. Journal of Astronautics, 2007, 28(4): 805-811 (in Chinese). [9] 翟光, 仇越, 梁斌, 等. 在轨捕获技术发展综述[J]. 机器人, 2008, 30(5): 467-480. ZHAI G, QIU Y, LIANG B, et al. Development of on-orbit capture technology[J]. Robot, 2008, 30(5): 467-480 (in Chinese). [10] 邓宗全, 李龙, 李兵, 等. 空间抓取装置性能综合分析及评价[J]. 机械设计, 2012, 29(3): 1-6. DENG Z Q, LI L, LI B, et al. Comprehensive analysis and evaluation on performance of space grappling device[J]. Journal of Machine Design, 2012, 29(3): 1-6 (in Chinese). [11] 张玉军, 冯书兴. 主动式空间碎片清理研究[J]. 装备指挥技术学院学报, 2010, 21(6): 78-82. ZHANG Y J, FENG S X. Research on active space debris removal[J]. Journal of the Academy of Equipment Command & Technology, 2010, 21(6): 78-82 (in Chinese). [12] BONNAL C, RUAULT J M, DESJEAN M C. Active debris removal: Recent progress and current trends[J]. Acta Astronautica, 2013, 85(4): 51-60. [13] ANDRENUCCI M, PERGOLA P, RUGGIERO A. Active removal of space debris expanding foam application for active debris removal[R]. Toscana : University of Pisa, 2011: 2-8. [14] BISCHOF B, KERSTEI L N, STARKE J, et al. Roger-robotic geostationary orbit restorer[J]. Science and Technology Series, 2004, 109: 183-193. [15] ANSELMO L, PARDINI C. Space debris mitigation in geosynchronous orbit[J]. Advances in Space Research, 2008, 41(7): 1091-1099. [16] XU W F, LIANG B, GAO D, et al. A space robotic system used for on-orbit servicing in the geostationary orbit[C]//2010 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Piscataway, NJ: IEEE Press, 2010: 4089-4094. [17] XU W F, LIANG B, LI B, et al. A universal on-orbit servicing system used in the geostationary orbit[J]. Advances in Space Research, 2011, 48(1): 95-119. [18] BERGAMIN L, IZZO D. Comments on deployment and control of charged space webs:ACT-RPT-MAD-ARI-05-4109[R].Sweden: Advanced Concepts Team, ESA, 2007: 2-4. [19] MANKALA K K, AGRAWAL S K. Dynamic modeling and simulation of impact in tether net gripper systems[J]. Multibody System Dynamics, 2004, 11(3): 235-250. [20] MANKALA K K, AGRAWAL S K. Dynamic modeling and simulation of satellite tethered systems[J]. Journal of Vibration and Acoustics, 2005, 127(2): 144. [21] YU Y, BAOYIN H X, LI J F. Dynamic modelling and analysis of space webs[J]. Science China Physics, Mechanics and Astronomy, 2011, 54(4): 783-791. [22] HUANG P F, ZHANG F, MA J, et al. Dynamics and configuration control of the maneuvering-net space robot system[J]. Advances in Space Research, 2015, 55(4): 1004-1014. [23] ASLANOV V, YUDINTSEV V. Dynamics of large space debris removal using tethered space tug[J]. Acta Astronautica, 2013, 91(10): 149-156. [24] ZHAI G, QIU Y, LIANG B, et al. On-orbit capture with flexible tether-net system[J]. Acta Astronautica, 2009, 65(5-6): 613-623. [25] BAOYIN H X, YU Y, LI J F. Orbital maneuver for a rotating tethered system via tidal forces[J]. Journal of Spacecraft and Rockets, 2013, 50(5): 1060-1068. [27] JIA J, WANG Y. Simulation of fiexible net capture process for space debris[J]. Spacecraft Environment Engineering, 2014, 31(2): 136-140. [28] 陈钦, 杨乐平. 空间绳网系统发射动力学问题研究[J]. 宇航学报, 2009, 30(5): 1829-1833. CHEN Q, YANG L P. Research on casting dynamics of orbital net systems[J]. Journal of Astronautics, 2009, 30(5): 1829-1833 (in Chinese). [29] 陈钦. 空间绳网系统设计与动力学研究[D]. 长沙: 国防科学技术大学, 2010: 67-98. CHEN Q. Design and dynamic of an orbital net-capture system[D]. Changsha: National University of Defense Technology, 2010: 67-98 (in Chinese). [30] 李强. 空间绳系卫星系统动力学建模及仿真研究[D]. 长沙: 国防科学技术大学, 2007: 20-45. LI Q. Study on space tethered satellite system dynamic modeling and simulating[D]. Shangsha: National University of DefenseTechnology, 2007: 20-45 (in Chinese). [31] 赵国伟, 熊会宾, 黄海, 等. 柔性绳索体展开过程数值模拟及实验[J]. 航空学报, 2009, 30(8): 1429-1434. ZHAO G W, XIONG H B, HUANG H, et al. Simulation and experiment on deployment process of flexible rope[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(8): 1429-1434 (in Chinese). [32] ROGER-Team.ROGER—Phase A final report executive summary[R]. Sweden: Advanced Concepts Team, ESA, 2003. [33] PALMERINI G B, SGUBINI S, SABATIN M I. Space webs based on rotating tethered formations[J]. Acta Astronautica, 2009, 65(1-2): 131-145. [34] FUJIWARA J, SEGAWA S, ODA K, et al. Static loading tests and a computational model of a flexible net[C]//Extended Abstracts of International Symposium on New Olympics New Shell and Spatial Structures. Tokyo: Architectural Institute of Japan, 2007: 66-72. [35] 陈钦, 杨乐平, 张青斌. 空间飞网发射动力学建模仿真研究与地面试验[J]. 国防科技大学学报, 2009, 31(3): 16-19. CHEN Q, YANG L P, ZHANG Q B. Dynamic model and simulation of orbital net casting and ground test[J]. Journal of National University of Defense Technology, 2009, 31(3): 16-19 (in Chinese). [36] 李京阳, 于洋, 宝音贺西. 空间飞网系统抛射参数优化研究[J]. 宇航学报, 2012, 33(6): 823-829. LI J Y, YU Y, BAOYIN H X. Projecting parameters optimization for space web systems[J]. Journal of Astronautics, 2012, 33(6): 823-829 (in Chinese). [37] 李京阳, 于洋, 宝音贺西, 等. 空间飞网两种动力学模型的比较研究[J]. 力学学报, 2011, 43(3): 542-551. LI J Y, YU Y, BAOYIN H X, et al. Simulation and comparison of different dynamical models of space webs[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(3): 542-551 (in Chinese). [38] WANG X H, WAN C H, SUN C C, et al. An optimization algorithm for multi-objective optimization problem by using envelope-dual method[J]. Procedia Engineering, 2013, 67: 457-466. [39] 王晓慧, 樊思思, 李人杰. 改进的螺栓连接结构建模方法及其在导弹设计中的应用[J]. 固体火箭技术, 2014, 37(5): 694-698. WANG X H, FAN S S, LI R J. A modified modeling method of bolted connection andits application to the missile design[J]. Journal of Solid Rocket Technology, 2014, 37(5): 694-698 (in Chinese). 王晓慧女,博士,讲师。主要研究方向:结构与多学科优化,复杂系统优化,飞行器总体设计。 Tel.: 010-82338763 E-mail: xhwang@buaa.edu.cn 万长煌男,硕士。主要研究方向:飞行器总体设计,结构动力学。 E-mail: wan_ch@foxmail.com URL:www.cnki.net/kcms/detail/11.1929.V.20160322.1600.004.html Parameteroptimizationdesignmethodofcomplexspace-websystem WANGXiaohui*,WANChanghuang,XIARenwei SchoolofAstronautics,BeihangUniversity,Beijing100083,China Space-websystemwovenbylightweightandpliableropeisaconceptproposedforcapturingnon-cooperativetargetonorbits,andithasagreatapplicationprospectindealingwithspacedebrisanddeadspacecraft.Afterbeingthrownfromaplatform,itformsunstableconfigurationinspace.Itsdeployingperformanceisgreatlyinfluencedbyinitialparameters.Theoptimizationofparametermatchingisakeytechnologyforthespace-websystemdesignandtest.Thepaperproposeserror-toleranceasaquantitativedescriptionaboutthecapturingperformanceofspace-websystemandestablishesanoptimizationmathematicalmodelwhereerrortoleranceistheobjectivefunction.Takecapturingatargetinacertaindistanceasanexample,theIsightandANSYS/LS-Dynaarecombinedtosolvethemathematicalmodelandtheoptimaldesignisobtained.Thesimulationoftheoptimaldesignverifiesthevalidityofoptimizationmodel.Finally,thestabilityoftheoptimaldesignisdiscussedbyorthogonalexperimentandrangeanalysis.Theresearchprovidessomereferenceforthedesignofspace-websystem,thesystemtestsonthegroundandinspaceandtheapplicationofthespace-webinthefuture. space-websystem;parametermatching;optimizationmodel;errortolerance;DOE 2015-09-19;Revised2015-11-03;Accepted2016-02-29;Publishedonline2016-03-221600 s:TheFundamentalResearchFundsfortheCentralUniversities(YWF-13-ZY-02;YWF-14-FGC-024) .Tel.:010-82338763E-mailxhwang@buaa.edu.cn 2015-09-19;退修日期2015-11-03;录用日期2016-02-29; < class="emphasis_bold">网络出版时间 时间:2016-03-221600 www.cnki.net/kcms/detail/11.1929.V.20160322.1600.004.html 中央高校基本科研业务费专项资金 (YWF-13-ZY-02;YWF-14-FGC-024) .Tel.:010-82338763E-mailxhwang@buaa.edu.cn 王晓慧, 万长煌, 夏人伟.一种复杂空间飞网系统参数优化设计方法J. 航空学报,2016,37(10):3064-3073.WANGXH,WANCH,XIARW.Parametersoptimizationdesignmethodofcomplexspace-websystemJ.ActaAeronauticaetAstronauticaSinica,2016,37(10):3064-3073. http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn 10.7527/S1000-6893.2016.0057 V19; V476.5 A 1000-6893(2016)10-3064-10



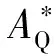

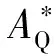


4 结 论
