基于伴随方程的网格自适应及误差修正

崔鹏程， 邓有奇， 唐静， 李彬

中国空气动力研究与发展中心 计算空气动力研究所， 绵阳 621000

基于伴随方程的网格自适应及误差修正

崔鹏程， 邓有奇， 唐静*， 李彬

中国空气动力研究与发展中心 计算空气动力研究所， 绵阳 621000

基于流场方程的离散伴随优化理论和三维非结构网格，建立了网格自适应技术和目标函数误差修正方法。详细研究了用流动伴随变量进行目标函数的误差估计和修正技术，构造了适用于格心格式有限体积法的流场变量插值技术和网格单元剖分判据，初步实现了网格物面投影和空间单元优化，发展了适用于有限体积法的整套网格自适应方法。对NACA0012翼型和ONERA-M6机翼绕流进行了自适应数值模拟，并对升、阻力等目标函数进行了误差修正。数值结果表明，本文自适应方法能正确地捕捉到影响目标函数计算精度的敏感区域，网格自适应和误差修正两项技术显著提高了升、阻力等目标函数的计算精度。

非结构网格； 伴随方程； 目标函数； 误差修正； 网格自适应

飞行器气动力的高精度预测是计算流体力学一直以来追求的目标。计算精度既取决于所使用的数值格式精度，也取决于计算网格的质量。网格质量不仅影响计算精度，还影响计算收敛性。人为地全局加密和预测流场特征并局部加密是两种获得足够网格分辨率的常用方法。对于复杂流场或不熟悉的流场，往往通过全局加密或试算的方法来解决。全局加密不仅浪费计算资源，还会延长计算时间。预测流场特征需要大量的工程实践经验，并且面对新型复杂飞行器仍需不断的摸索和学习。网格自适应技术是一种自动优化计算网格、提高流动模拟精度的有效方法。

近年来局部网格加密的自适应技术在非结构网格中得到广泛研究。现有的大多数自适应方法都基于流场特征进行自适应加密，如激波、边界层、旋涡、尾流、滑移线或驻点等。基于流场特征的网格自适应方法假设局部误差与流动特征量相关，利用流场特征探测器(如梯度探测器、熵增探测器、法向马赫数探测器等)标识需要加密网格的流场区域，通过局部网格加密减小流场局部误差。该方法致力于减小流场特征处的误差，忽略了影响目标函数全局误差的其他区域。该自适应方法只捕捉流场特征，不一定能提高流场的全局计算精度[1]。

基于伴随方程的网格自适应方法[1-2]，更能有效地提高全机气动特性模拟精度。该方法通过伴随方程直接建立局部误差与目标函数全局误差之间的关系，可直接度量局部误差对全局误差的影响，对目标函数的全局误差进行估计和修正。该方法在设定目标函数全局误差上限后，通过自适应加密对全局误差产生较大影响的网格区域，使计算误差在网格单元间均匀分布并减小到给定的误差上限以下。相比基于流动特征的自适应技术，达到相同的计算准度，该方法增加的网格量更少，能构造基于计算精度的自适应终止判据，对飞行器的气动设计更有指导意义[3-4]。

国内外很多学者对基于伴随方程的网格自适应和误差修正技术进行了研究。Park[5-8]发展了基于伴随方程的三维各项同性网格自适应方法，并探索了混合网格的自适应和误差修正技术；Park等[9]发展了结构网格的伴随自适应与误差估计理论，对音爆问题进行了探讨；Oliver和James等[10-11]将伴随自适应与高阶算法相结合，大幅提高了目标函数计算的准确性；Yamaleev和Diskin[12-13]针对非定常问题研究了二维各向异性非结构网格的伴随自适应和误差修正；国内杨振虎和周磊[14]探索了二维非结构网格的自适应技术，杨夏勰和周春华[15]发展了一种多目标函数修正的二维非结构网格自适应方法。

但是现有的大部分文献主要研究格点格式有限体积法的误差修正及自适应方法，对格心格式有限体积法的误差修正和自适应方法研究较少。格心格式有限体积法在边界条件处理和基于面的循环遍历等方面更有优势，在工程中应用广泛。国内学者对基于伴随方程的目标函数误差修正方法研究较少，也无人介绍基于伴随方程的误差修正方法在三维非结构网格的应用。

本文基于三维非结构网格和离散伴随方程理论，发展了一种适用于格心格式有限体积法的网格自适应方法和升力、阻力等目标函数误差修正方法。经过数值试验验证，该方法能明显提高目标函数的计算精度。

1 数值方法

1.1 流场方程

本文使用的流场解算器为自主研发的MFlow软件[16]，时间离散使用LU-SGS (Lower-Upper Symmetric Gauss-Seidel)方法[17]，如无特殊说明，无黏通量离散使用Roe格式[18]。本文针对无黏流动研究纯四面体网格的自适应和误差修正方法，控制方程采用守恒型三维欧拉方程,即

(1)

式中：U为流动解向量;F、G、H为通量项。在定常情况下∂U/∂t=0，欧拉方程简化为

(2)

1.2 伴随方程

得到流场方程的离散解之后，目标函数f(如升力、阻力和力矩等)可以表示为流场离散解U的函数，f=f(U)，目标函数对流场变量求导，由链式法则得

(3)

式中：R为流场方程的残差;定义伴随变量Ψ为目标函数对离散残差的敏感度[6],即

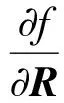
(4)

综合式(3)与式(4)，得到伴随方程为

(5)

文中伴随方程求解采用LU-SGS方法[19]和多重网格技术[20]，数值离散格式与流场方程离散格式保持一致。

1.3 误差修正

假设存在两套不同的网格，粗网格ΩH和细网格Ωh，粗网格和细网格上计算的目标函数分别记为fH(UH)和fh(Uh)，H与h分别为粗网格和细网格的尺度。粗网格消耗的计算资源较少、计算时间也较短，但计算得到的目标函数准确度不高。细网格上计算的目标函数准确度很高，但是往往消耗大量的计算资源及计算时间。通过对fH(UH)进行修正获得fh(Uh)的近似值是可以期待的[5,21]。本文用伴随方程修正目标函数的方法来自文献[5,21]，简述如下。

(6)

(7)

把式(7)代入到式(6)中，得到细网格上目标函数的估计值：

(8)

引入伴随方程：

(9)

则式(8)可写为

(10)

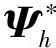
(11)

(12)

(13)

1.4 自适应参数

假设插值足够精确，则式(11)对线性目标函数的修正是精确的，但在实际应用中目标函数往往是非线性的。对非线性目标函数，式(11)还有一定剩余误差，希望通过网格自适应减少目标函数修正后的剩余误差，故将剩余误差设为自适应参数。自适应参数的设置方法来自参考文献[6,21]，简述如下。将式(10)进一步展开整理得

(14)

则目标函数修正后的剩余误差为

(15)

式(15)中剩余误差是伴随解的误差和流场方程残差的内积。根据伴随方程进一步推导[6]可得另一种形式的剩余误差，如式(16)可以表示成伴随方程残差和流场方程解误差的内积。

(16)

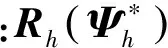
(17)

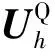
(18)

(19)

把这两种形式的剩余误差绝对值的均值设为自适应参数，则自适应参数ε表示为

(20)

2 自适应策略

2.1 粗网格剖分方法

基于伴随方程的误差估计和网格自适应方法需要构造一套密网格，本文通过把粗网格全局剖分细化得到内嵌细网格，从而修正全局目标函数和计算自适应参数。四面体网格单元的剖分方式有一分二、一分四、一分八等[22]。

如图1所示，四面体一分二和一分四方法得到的小四面体与原四面体不相似，若原四面体质量较差，剖分后得到的小四面体质量将更差。为了使剖分后的网格尽可能地保持原四面体的形状，本文中，统一采取一分八的网格剖分方法，即在每个四面体的边上添加一个新的网格点，将原四面体剖分为8个小四面体。四面体一分八由于点的连接方式不同，有3种不同的剖分方式，本文选取使内嵌细网格的最大二面角最小的一种剖分方法。

图1 粗网格剖分方法Fig.1 Methods to divide coarse grid

2.2 插值技术

在修正目标函数和计算自适应参数时，需计算粗网格流场解和伴随解在细网格上的插值解。因此，一种准确的插值方法至关重要。很多文献采用格点格式有限体积法，流场变量和伴随变量存储在网格节点处，因此大部分文献采用节点插值法[5-6]。本文使用格心格式有限体积法，流场变量和伴随变量存储在网格形心处[23]，若参照节点插值法，则细网格上插值解的准确度不高。因此，本文提出了一种多项式插值法，直接将流场变量和伴随变量从粗网格体心插值到细网格体心处，其基本思路如下。

对于低阶插值，假设流场变量和伴随变量在网格单元k内线性分布，满足线性方程：

q=a+bx+cy+dz

(21)

式(21)有4个未知系数a、b、c和d，如图2所示，假设在与该网格单元共点的所有m个网格单元内，流场变量和伴随变量也满足该线性多项式，则会形成m个线性方程：

qi=a+bxi+cyi+dzii=1，2，…，m

(22)

再用最小二乘法求解该线性方程组，得到各项系数。由于距离的不同，网格单元k周边的网格单元对其影响不同，故求解方程组时对各网格单元所对应的方程设置不同的权重，离网格单元k越近，权重越大。设置权重wr为

wr=1/l2

(23)

式中：l为各网格单元和网格k形心间的距离。得到多项式各系数后，把各细网格形心坐标代入线性方程，就可以得到细网格上的低阶插值。

同理对于高阶插值，假设流场变量和伴随变量在网格单元k内呈二次分布，满足二次方程：

q=a+bx+cy+dz+ex2+fy2+

gz2+hxy+lxz+myz

(24)

式(24)有10个未知系数，与低阶插值类似，假设在与该网格单元共点的所有m个网格单元内，流场变量和伴随变量也满足该二次多项式，则会形成m个二次方程：

(25)

式中：j=1，2，…，m。

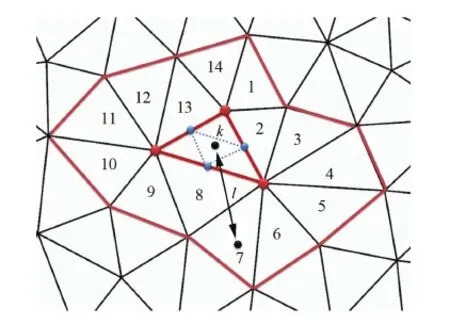
图2 二维多项式插值法Fig.2 Two-dimensional interpolation method using polynomial

与线性插值类似，用最小二乘法求解带距离权的二次方程组，可得细网格上的高阶插值。

2.3 自适应判据

自适应的目标是降低目标函数修正后的剩余误差，即减小计算域内自适应参数的值。内嵌在粗网格内的细网格构造好以后，可以方便计算每个粗网格单元k的自适应参数εk：

(26)

式中：εk为粗网格单元k内的内嵌细网格单元自适应参数之和;lk为粗网格单元k的细网格单元集。定义局部自适应准则：

(27)

此外，定义全局自适应参数ε为所有粗网格自适应参数之和，即ε=∑εk。ε虽然并不是准确的目标函数的全局误差，但是ε是全局误差的一种度量[6]。由此，一种全局的自适应判据可以定义为

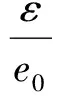
(28)

当ηz>1，即粗网格上的目标函数全局误差大于人为设定的误差上限，网格需要进一步细化。与文献[6]类似，本文结合ηk和ηz，设定综合自适应判据，对每个粗网格单元k，判断ηzηk，若ηzηk>1，则标记该网格单元k需要细化，若ηzηk<1，则该网格单元k无需细化。

2.4 网格优化

对于物面上的粗网格单元，剖分成细网格后新添加的网格点通常不在物面上，需要将新网格点投影到物面上以保持网格与物面的相容性。

如图3所示，对于物面网格，本文利用两节点X1、X2及其法向与切向信息N1、N2，r1、r2构造出物面曲线的二次拟合曲线，将自适应新加入的点XNEW移动到拟合曲线的中点。物面网格投影之后，用距离权函数方法[24]移动相应的空间网格，保持空间网格与物面网格的相容性。

图3 物面投影方法Fig.3 Projection method on surface geometry

图4 Laplacian网格光滑方法Fig.4 Laplacian method to smooth grid

自适应后的网格质量检测及网格光滑对于自适应技术也起到重要的作用。通常，由自适应得到的网格局部质量不高，需要光滑处理。本文采用Laplacian光滑方法[22]，如图4所示，Laplacian光滑方法是将网格点Vi移动到相邻网格点(V1,V2，…，VN)的形心Vc处，使网格布局均匀分布，通过网格光滑可以改善自适应网格局部疏密不均的情况。

2.5 自适应流程

基于伴随方程的自适应是一个迭代过程，图5 为其流程图。首先把初始粗网格全局剖分细化得到内嵌的细网格，并构造高阶插值与低阶插值。然后计算局部自适应参数与全局自适应参数，对目标函数进行修正。最后判断是否满足自适应判据，若满足则自适应过程结束，若不满足，则标记需要加密的粗网格并加密，把自适应网格优化之后进行下一轮自适应过程，直到满足自适应判据为止。

图5 自适应迭代过程Fig.5 Iteration process of adaptation

3 算例分析

本文采用NACA0012翼型和ONERA-M6机翼对所建立的非结构网格自适应方法进行了验证，控制方程为欧拉方程，网格为纯四面体非结构网格。为了校验网格自适应和目标函数误差修正的效果，本文将一系列均匀加密的网格与自适应网格作对比，把均匀加密网格计算结果的Richardson外插值或极其精密网格的计算结果当做期望值。

3.1 NACA0012翼型

NACA0012翼型扰流流场来流条件为：来流马赫数Ma∞=0.8,迎角α=1.25°，来流温度T∞=279.3 K,雷诺数Re=9×106。目标函数为阻力系数CD，每次自适应过程将误差上限设为上次自适应阻力系数的10%。

图6是NACA0012翼型原始网格与自适应后的对称面网格分布，自适应网格本身就反应了一定的流场特征，自适应后的网格在机翼前缘、后缘和机翼上下表面的强弱激波处都有明显的加密，因为这些网格区域对NACA0012翼型的阻力系数影响较大。

图6 NACA0012翼型自适应前后网格Fig.6 NACA0012 airfoil grid before and after adaptation

图7是NACA0012翼型原始网格与伴随自适应网格计算得到的压力分布p，从原始网格的压力分布可以看出，机翼上表面捕捉到的强激波范围较大，机翼下表面基本捕捉不到弱激波。而自适应后网格计算得出的上表面强激波与机翼下表面弱激波都很精细，压力等值线非常光滑。伴随自适应网格精确地捕捉到了NACA0012机翼的流场特征。

图8给出了NACA0012翼型的阻力系数随自适应次数与网格量的变化曲线。随着自适应次数的递增，网格量不断加大，阻力系数逐渐收敛到外插值。从图8可以看出，阻力系数误差修正效果明显，相同网格量，经过误差修正后阻力系数的计算准确度比全局加密网格的准确度提高了15.50%。

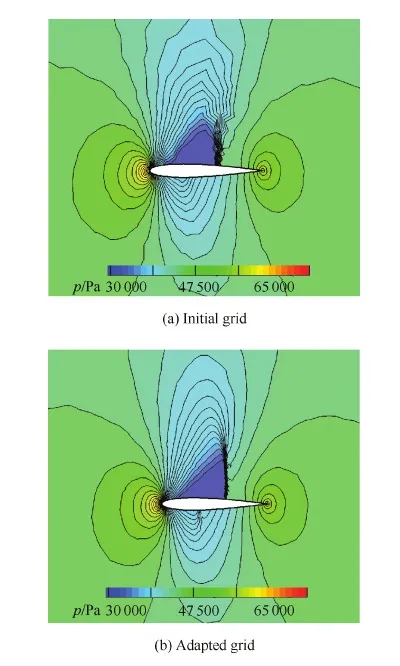
图7 NACA0012翼型自适应前后压力分布Fig.7 Pressure distribution of NACA0012 airfoil before and after adaptation

图8 NACA0012翼型阻力系数自适应Fig.8 Drag coefficient adaption of NACA0012 airfoil

3.2 ONERA-M6机翼

1) 目标函数为阻力系数

目标函数为阻力系数CD，每一次自适应过程将误差上限设为上一次自适应过程阻力系数的10%。计算状态选择为：Ma∞=0.84,α=3.06°，T∞=255.56 K,Re=1.172×107。在该计算状态下，机翼表面为附着流，机翼上表面有λ型激波。

图9是ONERA-M6机翼自适应前后的上表面网格分布与空间网格分布，可以看出，自适应后的网格在机翼前缘、后缘和激波处有明显的加密，在远离机翼表面的区域网格加密较少。离机翼表面较远的网格区域对阻力系数的贡献较小，机翼前后缘以及激波等网格区域对阻力系数贡献很大。

图9 ONERA-M6机翼阻力系数自适应前后网格Fig.9 ONERA-M6 wing grid before and after adaptation for drag coefficient

图10是文献[5]中的自适应网格，与本文的自适应结果基本一致。

图11是用ONERA-M6机翼原始网格与自适应网格计算得到的压力分布，从原始网格的压力分布可以看出，机翼上表面的激波范围较大，而从自适应后的压力分布可以看到精细的激波分布，压力等值线非常光滑，这说明伴随自适应在流场特征处有明显的加密，能较好地捕捉到流场特征。

图10 文献[5]中ONERA-M6机翼阻力系数自适应后网格 Fig.10 Adapted ONERA-M6 wing grid for drag coefficient in Ref.[5]

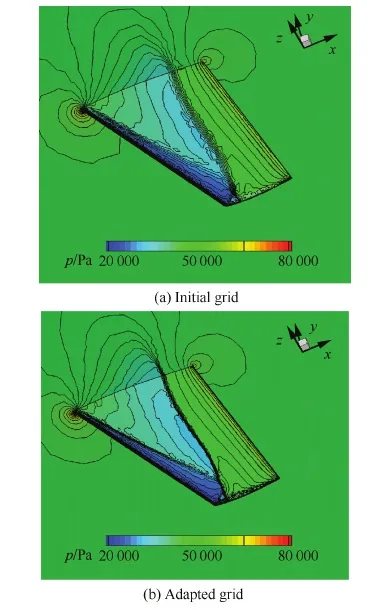
图11 ONERA-M6机翼阻力系数自适应前后压力分布Fig.11 Pressure distribution of ONERA-M6 wing before and after adaptation for drag coefficient

图12给出了ONERA-M6机翼阻力系数随自适应次数和网格量的变化曲线，可以看出，误差修正可以使阻力系数迅速地降到人工设定的误差范围以内。阻力系数的误差修正效果明显，相同网格量，经过误差修正后阻力系数的计算准确度比全局加密网格的准确度提高了17.74%，修正后的阻力系数与外插值很接近。同时数值试验发现，自适应网格比均匀加密网格计算收敛速度更快。由于自适应网格捕捉到了一定的流场特征，在对目标函数影响较大的区域进行大量加密，使残差更容易收敛，从而使目标函数的收敛速度更快。

图12 ONERA-M6机翼阻力系数自适应Fig.12 Drag coefficient adaption of ONERA-M6 wing

2) 目标函数为升力系数

此处采用的计算条件与目标函数为阻力系数时一致，但目标函数为升力系数CL。经过数值试验发现，升力系数对网格不是很敏感，经反复探索和参考国内外文献，每一次自适应过程将误差上限设为上一次自适应过程升力系数的5%。

图13是ONERA-M6机翼原始网格与自适应后的上表面网格分布与空间网格分布，可以看出，自适应后的网格在机翼前缘、后缘和激波处有明显的加密，因为这些网格区域对升力系数贡献很大。

图13 ONERA-M6机翼升力系数自适应前后网格Fig.13 ONERA-M6 wing grid before and after adaptation for lift coefficient

图14给出了用ONERA-M6机翼原始网格与自适应网格计算得到的压力分布，从原始网格的压力分布可以看出，机翼上表面的激波范围较大，压力等值线较粗糙，而从自适应网格的压力分布可以看到有精细的激波分布，压力等值线非常光滑。伴随自适应能较好地捕捉到流场特征。

图14 ONERA-M6机翼升力系数自适应前后压力分布Fig.14 Pressure distribution of ONERA-M6 wing before and after adaptation for lift coefficient

图15为升力系数随自适应次数和网格量的变化曲线，把一套极其精密网格的计算结果当做期望值来检验误差修正效果。相同网格量时升力系数的误差修正效果明显，经过误差修正后升力系数的计算准确度比全局加密网格的准确度提高了1.05%，误差修正能使计算的升力系数快速的接近期望值。同时数值试验也发现，由于自适应网格在对升力系数误差敏感的区域进行了自适应加密，自适应网格比均匀加密网格计算收敛速度更快。

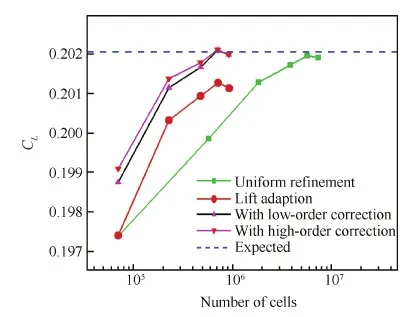
图15 ONERA-M6机翼升力系数自适应Fig.15 Lift ocefficient adaption of ONERA-M6 wing

从图12可以发现，在第4次自适应之后用自适应网格计算得出的阻力系数没有相同数量全局加密网格计算得出的阻力系数精确。图3为本文采用的物面网格投影方法示意图，用两节点及其法向构造出物面曲线的二次拟合曲线，将自适应新加入的点移动到拟合曲线的中点。这种投影方法在普通物面能较为准确地投影新添加的网格点，但是如图16所示，在机翼前后缘等物面曲率较大的区域，这种投影方法在局部区域不能与物面完全匹配，自适应后期由于投影误差累积使得自适应网格计算的阻力系数精度略低。数值模拟结果表明，这种投影方法对自适应过程和误差修正结果影响较小。

图16 拟合曲线投影方法Fig.16 Fitted curves projection method

4 结 论

1) 对比相同数量的全局加密网格，经过自适应迭代后的网格分布更为合理，气动力计算精度得到明显提高，为误差修正打下良好基础。

2) 采用本文误差修正方法对升力、阻力系数等目标函数进行修正，气动力计算精度进一步提高，并且随自适应迭代过程快速收敛到期望值。

3) 针对格心格式的有限体积方法，本文提出的流场变量和伴随变量多项式插值方法适应性好、插值精度高。

本文实现了纯四面体非结构网格的自适应和误差修正方法，下一步将开展混合网格(包含四面体、棱柱、金字塔等单元)的自适应和误差修正研究，并探索新的物面网格投影方法。

[1] PARK M A. Adjoint-based, three-dimensional error prediction and grid adaptation[J]. AIAA Journal, 2004, 42(9): 1854-1862.

[2] BECKER R, RANNACHER R. An optimal control approach to a posteriori error estimation in finite element methods[M]. 1st ed. Cambridge: Cambridge University Press, 2001: 1-102.

[3] FIDKOWSKI K J, DARMOFAL D L. Review of output-based error estimation and mesh adaptation in computational fluid dynamics[J]. AIAA Journal, 2011, 49(4): 673-694.

[4] GILES M B, SÜLI E. Adjoint methods for PDEs: A posteriori error analysis and postprocessing by duality[J]. Acta Numerica, 2002, 11: 145-236.

[5] PARK M A. Adjoint-based, three-dimensional error prediction and grid adaptation: AIAA-2002-3286[R]. Reston: AIAA, 2002.

[6] PARK M A. Three-dimensional turbulent RANS adjoint-based error correction: AIAA-2003-3849[R]. Reston: AIAA, 2003.

[7] PARK M A, DARMOFAL D L. Output-adaptive tetrahedral cut-cell validation for sonic boom prediction: AIAA-2008-6594[R]. Reston: AIAA, 2008.

[8] PARK M A. Low boom configuration analysis with FUN3D adjoint simulation framework: AIAA-2011-3337[R]. Reston: AIAA, 2011.

[9] PARK M A, AFTOSMIS M A, CAMPBELL R C. Summary of the 2008 NASA fundamental aeronautics program sonic boom prediction workshop: AIAA-2013-0649[R]. Reston: AIAA, 2013.

[10] OLIVER T A, DARMOFAL D L. An unsteady adaptation algorithm for discontinuous Galerkin discretizations of the RANS equations: AIAA-2007-3940[R]. Reston: AIAA, 2007.

[11] JAMES M Y, MODISETTE M, DARMOFAL D L. The importance of mesh adaptation for higher-order discretizations of aerodynamic flows: AIAA-2011-3852[R]. Reston: AIAA, 2011.

[12] YAMALEEV N K, DISKIN B, PATHAK K. Error minimization via adjoint-based anisotropic grid adaptation: AIAA-2010-4436[R]. Reston: AIAA, 2010.

[13] DISKIN B, YAMALEEV N K. Grid adaptation using adjoint-based error minimization: AIAA-2011-3986[R]. Reston: AIAA, 2011.

[14] 杨振虎, 周磊. 基于误差估计的伴随网格自适应方法[J]. 航空计算技术, 2011, 41(3): 14-16.

YANG Z H, ZHOU L. Output-based error estimation and grid adaptive mesh refinement[J]. Aeronautical Computing Technique, 2011, 41(3): 14-16 (in Chinese).

[15] 杨夏勰, 周春华. 目标函数误差估计及网格自适应处理[J]. 空气动力学学报, 2014, 32(5): 688-693.

YANG X X, ZHOU C H. Output-based error estimation and grid adaptation[J]. Acta Aerodynamica Sinica, 2014, 32(5): 688-693 (in Chinese).

[16] 张耀冰, 周乃春, 陈江涛. 小展弦比飞翼标模雷诺数影响数值模拟研究[J]. 空气动力学学报, 2015, 33(3): 279-288.

ZHANG Y B, ZHOU N C, CHENG J T. Numerical investigation of Reynolds number effects on a low-aspect-ratio flying-wing model[J]. Acta Aerodynamica Sinica, 2015, 33(3): 279-288 (in Chinese).

[17] KIM J S, KWON O J. Improvement on block LU-SGS scheme for unstructured mesh Navier-Stokes computations: AIAA-2002-1061[R]. Reston: AIAA, 2002.

[18] ROE P L. Approximate Riemann solvers, parameter vectors, and difference schemes[J]. Journal of Computational Physics, 1981, 43(2): 357-372.

[19] 李彬, 邓有奇, 唐静, 等. 基于三维非结构网格的离散型伴随方法[J]. 航空学报, 2014, 35 (3): 674-686.

LI B, DENG Y Q, TANG J, et al. Discrete adjoint method for 3D on unstructured grid[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(3): 674-686 (in Chinese).

[20] 李彬, 唐静, 邓有奇, 等. 并行的多重网格方法在离散伴随优化中的应用[J]. 航空学报, 2014, 35(8): 2091-2101.

LI B, TANG J, DENG Y Q, et al. Application of parallel multigrid algorithm to discrete adjoint optimization[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(8): 2091-2101 (in Chinese).

[21] VENDITTI D A, DARMOFAL D L. Grid adaptation for functional outputs: application to two-dimensional inviscid flows[J]. Journal of Computational Physics, 2002, 176(1): 40-69.

[22] 唐静, 郑鸣, 邓有奇, 等. 网格自适应技术在复杂外形流场模拟中的应用[J]. 计算力学学报, 2015, 32(6): 752-757.

TANG J, ZHENG M, DENG Y Q, et al. Grid adaptation for simulation of complicated configuration[J]. Chinese Journal of Computational Mechanics, 2015, 32(6): 752-757 (in Chinese).

[23] BLAZEK J. Computational fluid dynamics: principles and applications[M]. 1st ed. Oxford: Elsevier, 2001: 75-120.

[24] 唐静， 邓有奇， 马明生， 等. 飞翼气动优化中参数化和网格变形技术研究[J]. 航空学报, 2015, 36(5): 1480-1490.

TANG J, DENG Y Q, MA M S, et al. Parametrization and grid deformation techniques for fly-wing shape optimization[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(5): 1480-1490 (in Chinese).

崔鹏程男， 硕士， 研究实习员。主要研究方向： 非结构网格技术， 飞行器气动外形优化设计。

Tel: 0816-2463270

E-mail: ficojustdoit@163.com

邓有奇男， 博士， 研究员， 博士生导师。主要研究方向： 计算空气动力学， 飞行器优化设计。

Tel: 0816-2463007

E-mail: cai@cardc.cn

唐静男， 博士研究生， 助理研究员。主要研究方向： 飞行器气动外形优化设计， 非结构网格技术。

Tel: 0816-2463270

E-mail: tangjingn@foxmail.com

李彬男， 博士， 助理研究员。主要研究方向： 飞行器气动外形优化设计， 外挂物分离投放数值模拟。

Tel: 0816-2463091

E-mail: leebin2008@hotmail.com

URL：www.cnki.net/kcms/detail/11.1929.V.20160321.1035.002.html

Adjointequations-basedgridadaptationanderrorcorrection

CUIPengcheng，DENGYouqi，TANGJing*，LIBin

ComputationalAerodynamicsInstitute,ChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China

Basedonthediscreteadjointoptimizingtheoryandthree-dimensionalunstructuredgrid,agridadaptationtechnologyandanerrorcorrectionmethodforobjectivefunctionarebuilt.Amethodtopredictandcorrecttheerrorofobjectivefunctionusingadjointequationsispresented.Then,aninterpolationtechnologywhichsuitsforcentre-basedfinitevolumemethodisproposed,somemethodstodividetetrahedralgrids,projectsurfacegridsandoptimizespatialgridsarediscussed,andacompletegridadaptationsystemwhichsuitsforfinitevolumemethodisbuilt.Finally,thegridadaptationmethodisappliedtothesimulationofinviscidflowsaroundNACA0012airfoilandONERA-M6wing,andtheerrorofobjectivefunction,suchasthecoefficientofdragandlift,iscorrected.Numericalresultsshowthatthesensitivegridsforobjectivefunctionaredetectedandrefinedbythisgridadaptationmethod,andtheaccuracyofobjectivefunctionisobviouslyimprovedaftergridadaptationanderrorcorrection.

unstructuredgrid;adjointequation;objectivefunction;errorcorrection;gridadaptation

2015-11-24；Revised2016-02-17；Accepted2016-03-14；Publishedonline2016-03-211035

.Tel.：0816-2463270E-mailtangjingn@foxmail.com

2015-11-24；退修日期2016-02-17；录用日期2016-03-14； < class="emphasis_bold">网络出版时间

时间：2016-03-211035

www.cnki.net/kcms/detail/11.1929.V.20160321.1035.002.html

.Tel.：0816-2463270E-mailtangjingn@foxmail.com

崔鹏程， 邓有奇， 唐静， 等． 基于伴随方程的网格自适应及误差修正J． 航空学报,2016,37(10):2992-3002.CUIPC,DENGYQ,TANGJ,etal.Adjointequations-basedgridadaptationanderrorcorrectionJ.ActaAeronauticaetAstronauticaSinica,2016,37(10):2992-3002．

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0079

V211.3

A

1000-6893(2016)10-2992-11