四味真“题”提高学生计算思维

郭文静

2013版苏教版数学第一单元是《两三位数乘一位数》，本单元一共有课时17课时.学习内容较多，范围较广，对乘法竖式计算的要求较高.三年级作为低高年级的重要过渡期，同时也是计算逐步深入的学段.学生第一次接触竖式计算有很多不适应.在教学和练习过程中，笔者发现有很多问题：学生有的计算习惯较差导致计算错误，有的不懂算理只会算法导致算后不理解意义，有的数感较差对于估算问题无从下手，有的思维定势学了乘法竟然把加法当成乘法算……总之，诸多问题都是关于学生的计算思维能力需要提高.

数学课程标准提出：“应当注重发展学生的运算能力，主要是能够根据法则和运算律正确地进行运算能力.培养运算能力有助于学生理解运算的算理，寻求合理简洁的运算途径解决问题.”运算能力提高的前提在于学生形成一定的计算思维.

计算思维的高低是在学生计算的过程中发生和发展所表现出来的个性差异.心理学认为“学生的思维是后天培养的结果.思维能力的形成和提高有其自然发展的过程，但有意识、有目的、有系统的培养和训练，却起着关键性的作用.”所以笔者从学生的实际出发，以第一单元的练习题为蓝本，思考如何提升学生的计算思维.新版教材中的习题最常出现以下几种类型.

一、“火眼金睛”题，提高正确计算能力

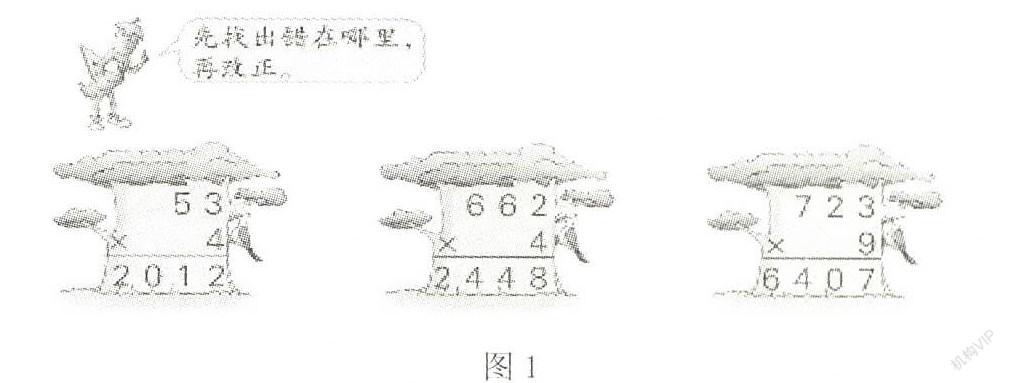
“火眼金睛”题几乎出现每个新课时后，这是一种比较常见的题型.有的教师在上这样的练习题时，只是让学生在旁边重新算一遍，然后判断正误.笔者认为这类题型并不在于直接改错，而是在于“找出错在哪里？” 比如，课上我要求学生先一题一题地看，找出错在哪里？学生都很积极说错在什么地方“进位数字没有写”“第一题得数的1应该写在横线上”……没有一个能准确说出错在哪一个地方.正确地找出错在什么地方，一方面是学生自己对两、三位数乘一位数竖式计算算法的一个巩固.能够在观察的过程中进一步熟悉算法和审视自己的计算思维，比如662×4，十位上6×4=24，满20要进2，百位上6×4+2=26.另一方面，是提高对算理的理解程度.可以用算理来检查错误性，比如53×4中，十位上的5×4=20，5是5个十，20就表示20个十，20个十是200，所以53×4只是200多，不会是2000多.[HJ1.45mm]

当然“火眼金睛”并不是只出现在书本上的练习中，同样也适用于平时的计算教学.当课上有很多计算题出现时，我会要求班上容易计算出错的学生到黑板上板演计算过程，然后我会要求班上的“毒眼小老师”进行批改.这时往往会出现一些意想不到的效果，批改的人检查得很认真，台下看的人也很认真，恨不得下一轮也轮到自己去当一会“毒眼小老师”，还有的人能说出错的人的出错原因.自此，上台板演的孩子们都写得很认真，写完还验算，就怕被别人改出错误，都养成验算的好习惯.

二、“双胞胎”题，培养严谨计算思维

13×5= 6×12= 5×16=

15×3= 2×16= 15×6=

“双胞胎”题往往是学生最容易出错的，由于学生因为年龄特征影响，总是会看题不仔细.心理学上说“瞬时记忆只有7个字符，而且只能保存1秒”.学生用这1秒的时间去记忆的7个字符很快就会模糊，更别提，把长得很像的“双胞胎”放在一起了，乍一看上去很像，等到实际计算时都不知道该用什么和什么相乘了.比如5×16和15×6的得数都算成了80. 这些都是因为没有严谨的计算思维造成.所以在练习时，可以要求学生用连一连的方式进行笔算式口算，从低位算起.如13×5，先算5×3=15，将5和3上面画弧线，再算5×10=50，将5和1上面画弧线，最后相加.用弧线将两两相连，让学生明确先算什么再算什么，提高计算的准确性，严谨性.

有些时候，学生作业中的得数和正确得数会差很多，我在仔细观察后发现原来是学生错将题目中的180抄成108.尤其是数学书25页第3题，（如308×5和380×5）我要求学生先观察四组题目找出相同和不同的地方：有一个乘数相同，另一个乘数的个位和十位颠倒了位置；再引导学生思考：中间有0的计算方法，末尾有0的计算方法.这样，在观察和分析清楚的情况下，学生既不会抄错题，也不会混淆计算的方法，那么，做好严谨计算的前提就是这种数字类似，数位相同，算法相对不同的计算对比题.

所以，教师在设计练习时，要以提高学生严谨的计算思维为前提，在考虑班上学生学情之后，设计一些 “双胞胎”对比题进行笔算或口算练习.在平时练习中就养成学生做题前先观察，先思考，再下笔的习惯，培养严谨的计算思维.

三、“找规律题”，提升敏捷计算思维

先算一算，再说说每组算式中的规律.

1×9+1 1×9+2 9×9+7

2×99+2 12×9+3 98×9+6

3×999+3 123×9+4 987×9+5

数学作为培养学生思维能力最佳途径的学科，其中寻找和发现事物之间的联系、规律、变化等内容构成了目前小学数学学习的重要内容.“找规律”题也是从小学一年级一直到六年级贯穿始末的经典题型.从当前的教学内容来看，三年级学生主要见过：（1）图形的排列和变化规律.要引导学生从颜色、形状、类型等多个方面来观察图形；（2）数字和数量的变化规律.同样也是要先从观察开始，然后总结出其规律.而上述题型就是本单元常见的练习，要想在错综纷杂的图形和的数字中找到正确的规律，绝不是一件容易的事情，要求学生有敏捷的计算思维为基础，以及教师正确的引导.

在教学中，我还是要求学生先观察再动笔算.比如第一方框中的三题，先让学生“说说题目的数字有什么特点？是怎样变化的？”生：“算式中第一个乘数依次增加，第二个乘数数位依次增加，最后一个加数也在增加；第一个乘数是几，就有几个9.”学生很快发现算式中的规律.接着就是计算，但是初学笔算时学生有很多会计算错误，导致与正确的规律失之交臂.这时我要求学生用乘法意义进行拆分“1×99+1”就是“99+1”；“2×99+2”就是“99+99+2”，也可以看作“99+99+1+1”，“得200.”再引导下学生很快看出规律.自然最后一个算式的答案就显而易见了.通过对不同方法，让学生真正掌握到观察的角度、方法和方式，使观察能力得到锻炼和提升；因此，有的时候未必要直接进行计算，而是根据计算特点和意义，敏捷的转换思路，换一个角度去发现规律，达到计算效果.

其次是培养学生大胆自信的品质.面对错综纷杂的数字，教师要鼓励学生充分相信自己，大胆地提升自己的设想，并沿着自己的设想继续进行.比如设计一下单个数字的规律探索题5，10，20（ ），（ ），（ ），我让学生自己先探索规律，然后集体交流.意外的是学生发现的数字间的规律是多种多样的，有的发现是两数之间的加法+5，+10，+15，+20，…，有的发现是乘法，两数之间的差距是×2.激励学生大胆猜想的同时，鼓励学生大胆交流，找出题目中隐藏的规律.发散思维的同时，学生能给出不同的想法，按照不同的想法同样可以接下去.这样教师才能更好地为学生敏捷思维提供一个锻炼的平台.

“找规律”题有利于培养学生良好的推理和思维能力.现在的教育多强调学生综合素质的提高，找规律的数学学习方法在提高学生计算能力的基础上，进一步培养了学生的计算思维和敏捷的推理能力.

四、“比较大小”，锻炼灵活计算思维

不计算，在○里填“>”或“<”.

13×5○31×5 502×6○500×6

240×3○420×3 7×620○602×7

教科书和配套练习中最常见的就是“比较大小”题，这类题型不仅考验了学生的算理和算法，还考验了学生运用所学知识的灵活性.就上面的例题而言，解决这种比较大小不再是单一的计算就行了，而是要联合算理和意义进行比较.

比如，31×5和13×5并不是只有计算才可以进行比较，可以用估一估的方法，一个是10×5大约50多，一个是30×5大约150多，然后进行比较.可是，不是所有题都能用估一估的方法，7×620和602×7，都是420多，怎么比较呢？.“当一个乘数相同时看另一个乘数，另一个乘数大，它们的积就大.”这是学生们自己总结出来的方法.面对不同的题，选择不同的方法.这样才能让比较更灵活，计算思维更灵活.

当然也有让人混淆的题目：203×4和204×3，有学生认为数字完全相同的情况下，都是二百多乘一位数，而且两道算式只是将乘数的个位和另一个乘数对调，那么结果应该是相等的.“火眼金睛”的题目已经难不倒孩子们了，用估一估的方法，结果显而易见.

通过这样的练习，既有效地帮助学生掌握了计算方法，加深对乘法意义的理解，又培养了学生灵活运用知识的能力.经常让学生从多角度进行思考，非常有利于学生思维灵活性的培养.

纵观这四种不同的真题，是书本中最常见的最基础的，但是对于初学乘法笔算的三年级孩子们而言，确是严谨的，敏捷的，灵活的.掌握好基础题型计算的教学，明确计算教学的意义，以培养学生计算能力，提高学生计算的思维，对我们教师而言是探索的，是深刻的，是长久的.