第9课“猜想验证性问题”复习精讲

刘振超

专题精讲

猜想验证是一种重要的数学思想方法，猜想验证问题给出的背景或条件是特定的，这些特定的背景或条件包括以下几个方面：有规律的数与式、等式，具有某种特征的图形、图表或流程图，特定的生活情景、数学问题等，一种情况是要求同学们从已知的个例中，通过观察、分析和比较，归纳出探究对象所具有一般规律或不变的结论，它能够揭示数学的本质，这些规律或结论可进一步指导我们解决相关的实际问题，它体现了“特殊→一般→特殊”的数学思想：另一种情况是要求同学们从一个问题的解题策略或结论，类比猜想出另一个相似问题的解题策略或结论，它体现了“转化”的数学思想，旨在让同学们学会知识的迁移，猜想验证问题在中考的选择、填空或解答题中均有考查，在选择题、填空题中以代数方面为主，在解答题中以几何方面为主，分值占到5%左右，

重点题型例新

一.数、式规律猜想型

数、式规律猜想型问题，通常给出一些数字、代数式、等式或不等式，要求猜想其中蕴涵的规律，解决此类问题的方法是：先写出数或式的基本结构，然后横比，即比较同一数或式中不同部分之间的数量关系，再纵比，即比较相邻数或式在相同位置的数量关系，找出各部分的共同特征，即各部分与对应序号的关系，对于有规律循环的要找出“循环节”，最后用字母代替数，即找到了规律。

点拨：当按某个规则算出一列数时，这列数常按某一循环节循环，解答时我们应多算各项，直到“循环节”出现为止，计算应仔细，如果计算错误就会找不出“循环节”，或找错“循环节”。

点拨：观察等式规律，着重分析以下三个方面：一是同一等式结果的各部分之间的数量关系；二是从上一个结果到下一个结果是如何变化的：三是每一个等式的结果与对应序号之间的数量关系，

二.图形、坐标规律猜想型

解决图形规律猜想问题，需要从简单的图形人手，抓住随着“编号”或“序号”的增加，后一个图形与前一个图形相比，在数量上增加（或倍数）情况的变化，把图形变化规律转化为数字变化规律，对于点的坐标规律猜想问题，主要观察点的横坐标和纵坐标随“序号”的增加，它们与序号之间的数量关系，如果点的坐标循环出现，要把“循环节”找出来。

例3（2015·山西）如图1是一组有规律的图案，它们是由边长相同的正方形和正三角形镶嵌而成，第（1）个图案有4个三角形，第（2）个图案有7个三角形，第（3）个图案有10个三角形，…，依此规律，第n个图案有___个三角形，（用含n的代数式表示）

解析：找出1与4，2与7，3与10，…之间的数量关系，然后用n代替序数可得到第n个图案的三角形个数。

第（1）个图案有4个三角形，4=3xl+1；第（2）个图案有7个三角形，7=3x2+1；第（3）个图案有10个三角形，10=3x3+1；…，故第n个图案有（3n+1）个三角形，

点拨：对于图形规律型问题既可以从结果的数字上进行分析，也可直观地观察图形，看图形是如何变化的，如本题，若把第1个图案看作在1个正三角形的基础上增加了3个正三角形和1个正方形，我们发现，以后每次构图都是这样的，由此也可以得到答案，

例4（2015·济南）在平面直角坐标系中有三个点A（1，-1）、B（-1，-1）、C（0，1），点P（0，2）关于A的对称点为Pl，P1关于B的对称点为P2，P2关于C的对称点为P3，按此规律继续以A、B、C为对称中心重复前面的操作，依次得到P4，P5，P6，…，则点P2015的坐标是（

），

A.（O，O）

B.（0，2）

C.（2，-4）

D.（-4，2）

解析：按照操作的规则找出前面几个点的坐标，观察横、纵坐标变化规律，若出现循环，则把“循环节”找出来，

因点P（0，2）关于A的对称点为Pl，点A（1，-1），故根据中点坐标公式，得P1（2，-4），同理可得P2（-4，2），P3（4，0），P4（-2，-2），P5（0，0），P6（0，2），P7（2，-4），…，我们发现，每6个点循环一次，“循环节”为P1（2，-4），P2（-4，2），P3（4，0），P4（-2，2），B（0，O），R（0，2），因2015÷6=335余5，故点P2015的坐标是（0，0），故诜A，

三.方法类比猜想型

此类试题的特点是给出一个问题的解题过程，让我们尝试解决另一个相似的问题，解题策略是：首先要领会已给出的解答过程的思想内涵，然后找出前后两个问题的相似之处，一方面借鉴，另一方面适当变通，

点拨：当待求关系式与示例的关系式形式不一样时，我们要尝试进行变形，至于如何变形才算形式一致呢？这需要我们在类比猜想中思考已知形式的本质所在，如本题，就是要变形为自变量与自变量倒数的和的形式，

中考命题预测

1.公务员行政能力测试中有一类图形规律题，可以运用我们初中数学中的图形变换再结合变化规律来解决，图2中问号格内的图形应该是（

），

2.如图3都是由同样大小的棋子按一定的规律组成，其中第①个图形有1颗棋子，第②个图形一共有6颗棋子，…，则第⑦个图形棋子的个数为（

），

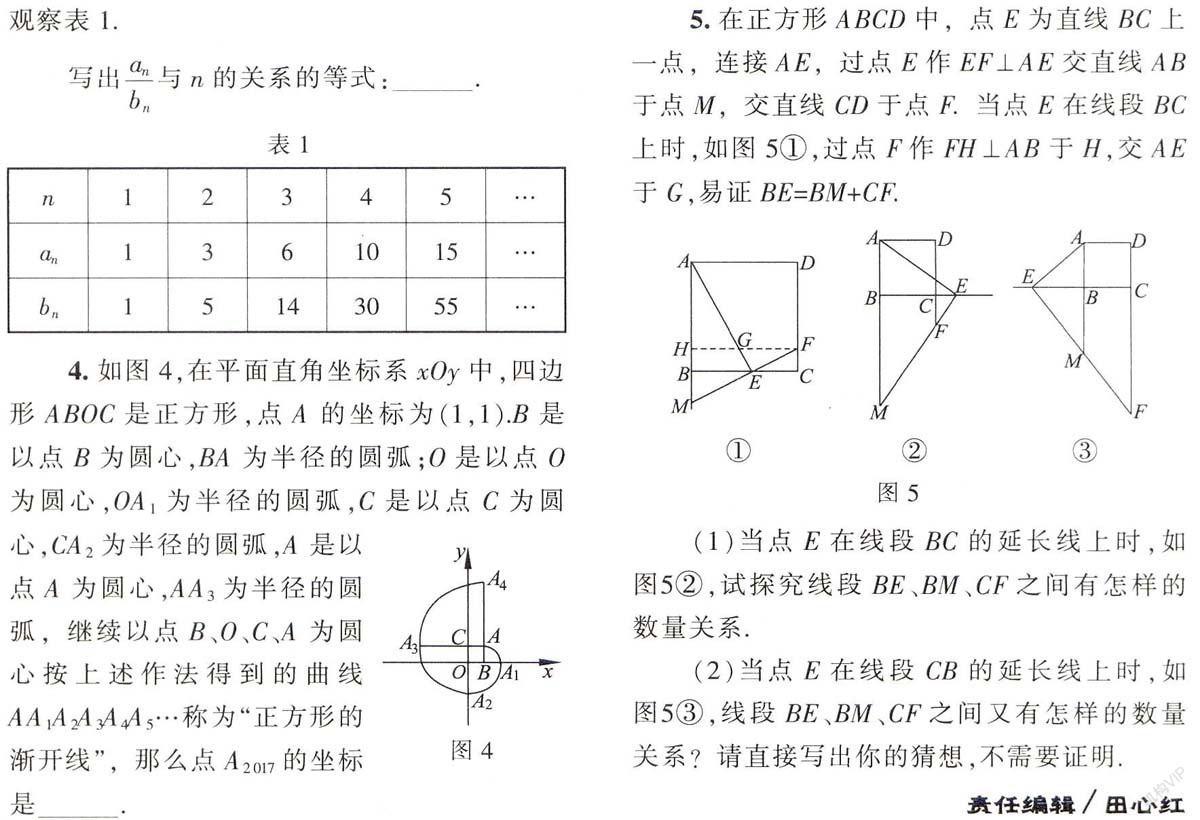
（1）当点E在线段BC的延长线上时，如图5②，试探究线段BE、BM、CF之间有怎样的数量关系，

（2）当点E在线段CB的延长线上时，如图5③，线段BE、BM、CF之间又有怎样的数量关系？请直接写出你的猜想，不需要证明。